Algo ABR

Identification

Infoforall

20 - Arbre Binaire de Recherche

⏪

⏬

⏩

1 - ABR

2 - Insertion

3 - Recherche

4 - FAQ

Nous avons vu qu'une implémentation des noeuds dans un tableau permet de trouver un noeud à coût constant pourvu qu'on connaisse parfaitement sa localisation. Il s'agit juste de la localisation d'un noeud par rapport à un autre, pas d'une recherche de clé.

Nous allons voir aujourd'hui un Arbre conçu spécifiquement pour pouvoir savoir où chercher facilement la clé qui nous intéresse.

Logiciel nécessaire pour l'activité : -

Prérequis :

  • Données : Arbre et Arbre Binaire
  • Algos : Parcours d'Arbres
  • Algos : Algorithmes des Arbres Binaires

Evaluation ✎ :

Documents de cours : open document ou pdf

Résumé : Version HTML ou fond blanc ou ou PDF (couleur ou gris)

1 - Arbre Binaire de Recherche (ABR)

⇩ ⇧ ⤊

(Rappel) 1.1 Coût d'une recherche dans un Arbre Binaire

Recherche classique : 𝞞(n)

Une recherche utilisant un parcours classique (en profondeur d'abord ou en largeur d'abord) est à coût linéaire en fonction de la taille n de l'arbre. Plus précisément, 𝞞(n) puisqu'on peut tomber par hasard sur la valeur lors de ce parcours.

Recherche ciblée : 𝞞(h)

Si la recherche permet de choisir entre direction gauche ou droite, la recherche est à coût linéaire en fonction de la hauteur h de l'arbre. Plus précisement, 𝞞(h) puisqu'on peut tomber sur la valeur avant d'atteindre le bas de l'arbre.

Puisque cette hauteur est fonction de la taille n de l'arbre et de la forme de l'arbre, on peut en déduire ceci :

  1. Une recherche ciblée est en 𝞞(log2(n)) dans un Arbre Binaire Parfait ou presque complet;
  2. Une recherche ciblée est en 𝞞(n) dans un Arbre Binaire Filiforme ou Dégénérée.
  3. Une recherche ciblée dans un arbre quelconque est entre les deux cas précédents mais cela donne encore 𝞞(n).
1.2 Arbre Binaire de Recherche (ABR)

Un Arbre Binaire de Recherche est un Arbre Binaire qui respecte une organisation ordonnée particulière.

Les clés des Noeuds doivent toutes pouvoir être comparées entre elles (c'est à dire disposer d'un opérateur < ou > ...).

La définition de l'Arbre Binaire de Recherche (ABR) impose que :

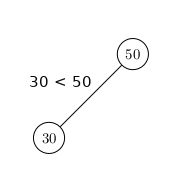
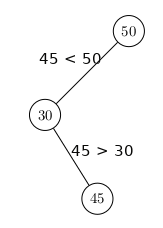
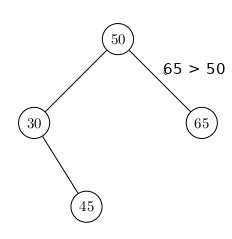
  1. toutes les clés du sous-arbre gauche soient plus petites* que la clé de la racine de l'Arbre étudié
  2. toutes les clés du sous-arbre de droite soient plus grandes* que la clé de la racine de l'Arbre étudié

La présence du * indique que l'égalité peut être traitée comme vous le voulez : à vous de choisir si vous voulez placer le cas EGAL à droite ou à gauche. Dans un premier temps, nous nous limiterons au cas des arbres pour lequel les clés sont toutes différentes.

On notera qu'on peut également faire l'inverse : mettre les plus grandes à gauche et les plus petites à droite.

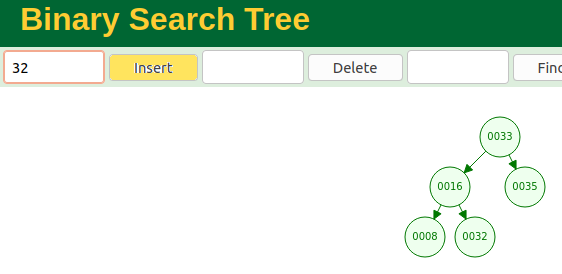
Exemples

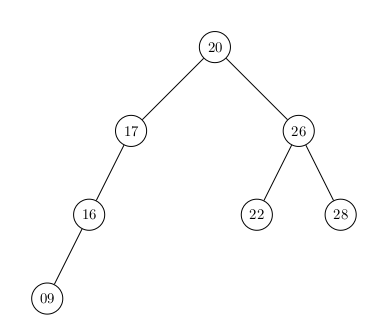
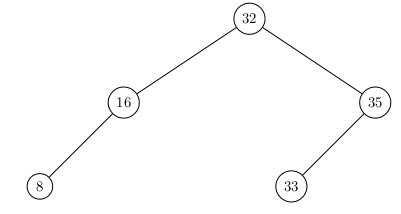
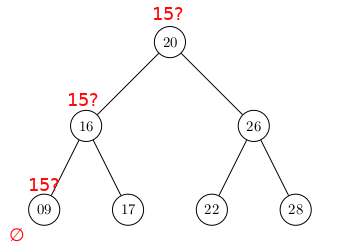
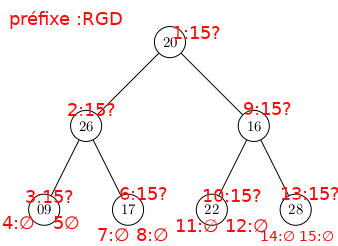
Un Arbre Binaire de Recherche parfait :

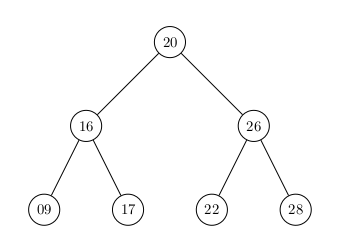
ABR complet

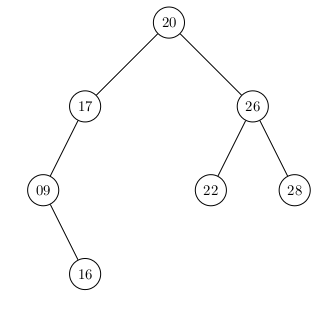
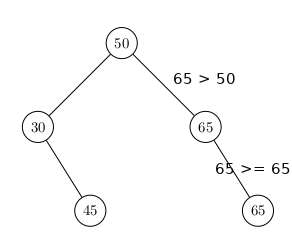
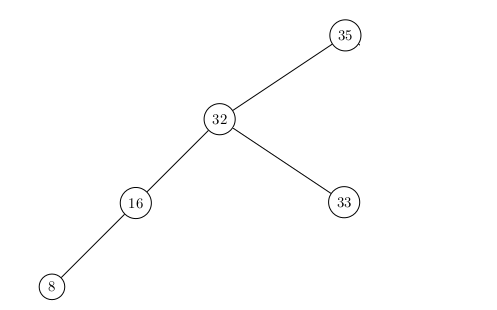
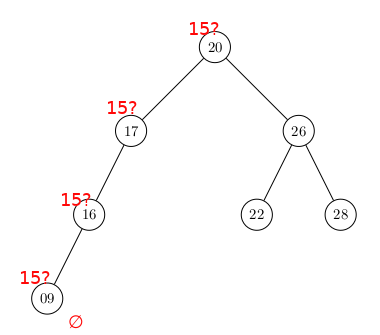
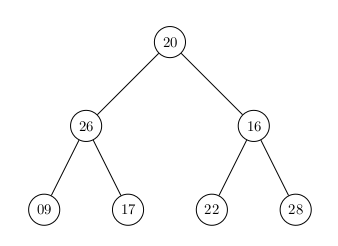
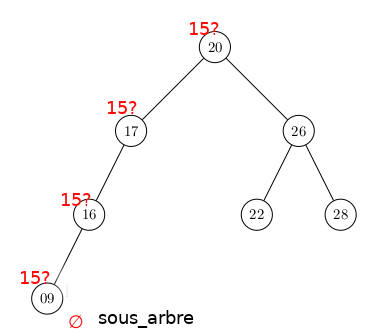
Les mêmes noeuds avec les mêmes clés dans une configuration moins optimale pour la recherche :

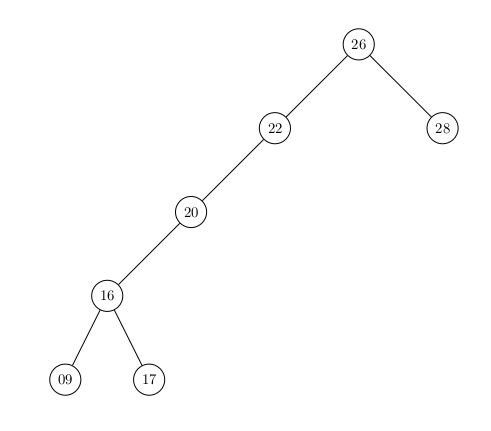
ABR quelconque

L'intérêt ?

Comme pour la liste-tableau trié qui permet une recherche dichotomique à coût logarithmique plutôt que linéaire, l'ABR permet une recherche à coût logarithmique (sur un Arbre proche d'un Arbre Complet) plutôt que linéaire.

En Anglais

En anglais, on dit Binary Search Tree ou BST.

01° Vérifier que

  • toutes les clés à gauche du Noeud de clé 20 sont inférieures à 20 et
  • toutes les clés à droite du Noeud de clé 20 sont supérieures à 20
ABR complet

02° Créer un nouvel Arbre Binaire de Recherche (ABR) un peu moins optimisé pour la recherche mais comportant les mêmes clés : la racine 20 mène à gauche à 17 et à droite à 26.

Trouver deux versions du sous-arbre gauche possibles.

Pourquoi cet Arbre est-il moins optimisé pour la recherche ?

...CORRECTION...

ABR question 2

Ou encore

ABR question 2 version 2

Il est moins optimisé que l'Arbre Binaire Complet puisqu'il possède un étage en plus : la recherche du noeud de clé 9 sera plus longue d'une étape.

1.3 Création d'un Arbre Binaire de Recherche

On commence par la racine puis on positionne progressivement les autres éléments, un à la fois.

Pour rajouter les noeuds (dont on connaît la clé) proposés, on suit ce principe :

  1. Partir de la racine
  2. Si la clé à placer est inférieure à celle du noeud actuel, on part à gauche.
    • Si le sous-arbre gauche est vide, on place la clé à gauche;
    • Sinon on répète l'opération en partant de la racine du sous-arbre gauche.
  3. Si la clé à placer est supérieure ou égale à celle du noeud actuel, on part à droite.
    • Si le sous-arbre droite est vide, on place la clé à droite;
    • Sinon on répète l'opération en partant de la racine du sous-arbre droite.

Exemple

On part de 50 et on rajoute 30.

ABR 50-30

On rajoute ensuite 45.

ABR 50-30-45

Puis 65.

ABR 50-30

Puis éventuellement à nouveau 65.

ABR 50-30

On notera donc qu'il faut faire très attention au cas des ABR lorsque des noeuds peuvent porter la même clé. Il existe des algorithmes d'insertion plus performants qui permettent de limiter la hauteur des AB si on rajoute plusieurs fois des clés identiques. On ne s'en préoccupera pas cette année.

04° Créer un nouvel Arbre Binaire de Recherche (ABR) dont les clés suivantes sont insérées progressivement : 32-16-8-35-33.

...CORRECTION...

ABR question 4

05° Même question en modifiant la place du 35 : 35-32-16-8-33.

L'ordre d'apparition des clés est-elle importante avec ce principe d'insertion ?

...CORRECTION...

ABR question 5

L'ordre des clés est effectivement à surveiller : on n'obtiendra pas le même arbre avec une séquence différente.

06° Utiliser le site proposé pour visualiser l'insertion de 33-35-16-8-32.

https://www.cs.usfca.edu/~galles/visualization/BST.html

Visualisation du site usfca.edu

2 - Algorithme d'insertion

⇩ ⇧ ⤊

Nous allons maintenant étudier l'algorithme ce que vous avez appliqué intuitivement.

Pour cela, nous allons avoir besoin des fonctions d'interface (ou primitives) vues précédemment mais également de deux nouvelles fonctions permettant d'insérer un nouvel Arbre Binaire de Recherche à gauche ou à droite :

(Rappel) 2.1 Les primitives (2e partie de la définition de l'arbre binaire)

Je le décris ici sous forme d'un type immuable, mais on pourait faire la même chose en muable.

  1. nvABV() -> Arbre Binaire VIDE

    2. Crée un nouvel ARBRE BINAIRE vide.
    On le note ainsi pour dire nouvelArbreBinaireVide() mais c'est plus long.

  2. nvAB(v:Element, g:Arbre Binaire, d:Arbre Binaire) -> Arbre Binaire NON VIDE

    3. Crée un nouvel ARBRE BINAIRE dont la racine porte la valeur v et mène aux sous-arbres transmis à la fonction, g et d.

  3. estABV(arbre:Arbre Binaire) -> bool

    4. Prédicat qui renvoie True si l'arbre est un arbre binaire vide.

  4. racine(arbre:Arbre Binaire NON VIDE) -> Noeud

    5. Renvoie le noeud jouant le rôle de la racine pour cet arbre binaire NON VIDE.

  5. contenu(noeud:Noeud) -> Element

    6. Renvoie l'élément rattaché au noeud transmis.

  6. gauche(arbre:Arbre Binaire NON VIDE) -> Arbre Binaire

    7. Renvoie le sous-arbre gauche de arbre. On obtient bien un Arbre. Si vous voulez le noeud gauche, il faudra appliquer en plus la fonction racine().

  7. droite(arbre:Arbre Binaire NON VIDE) -> Arbre Binaire

    8. Renvoie le sous-arbre droite de arbre.

2.2 Primitives supplémentaires dans un ABR

Les primitives ABR liées à l'insertion :

  1. inserer_gauche(arbre:AB NON VIDE, g:AB) -> None : on remplace le sous-arbre gauche de arbre par l'arbre g.
  2. inserer_droite(arbre:AB NON VIDE, d:AB) -> None : on remplace le sous-arbre droite de arbre par l'arbre d.

Les fonctions liées aux Noeuds :

Jusqu'à présent, nous n'avions considéré qu'une seule primitive appliquée à un Noeud, la fonction primitive contenu().

Mais en réalité, ce contenu peut se diviser en deux parties :

  • La clé ou l'étiquette du Noeud, son "nom"
  • Les données qu'on y stocke réellement, potentiellement énormement.

Ainsi, on peut considérer que contenu() renvoie l'ensemble de ces données. Pour filtrer l'une ou l'autre de ces données, rajoutons ceci :

  1. cle(noeud:Noeud) -> Cle : renvoie la clé du noeud.
  2. data(noeud:Noeud) -> Data : renvoie les données associées au noeud.

Regardons maintenant comment traduire l'insertion sous forme d'un algorithme.

2.3 Algorithme d'insertion d'un noeud dans un ABR (sans optimisation)

Principe général

L'algorithme proposé consiste à se déplacer dans l'ABR tant que la prochaine destination n'est pas un ABV.

On va donc s'arrêter sur le noeud qui deviendra le parent du noeud que nous allons rajouter.

Description des entrées / sortie

ENTREE 1 : un ABR NON VIDE avec lequel on veut travailler. Attention, deux préconditions : l'AB doit être NON VIDE et il doit respecter les critères des ABR.

ENTREE 2 : un Noeud (possédant une clé c et les données annexes éventuelles) qu'on veut rajouter à notre arbre. On notera que dans notre implémentaion simple, il n'y a pas de différence réelle entre un Noeud et un AB NON VIDE.

SORTIE : Vide, on modifie l'arbre sur place.

Description de l'algorithme

inserer_noeud_dans_ABR(arbre:ABR NON VIDE, noeud:Noeud) -> Vide

    étape 1 : initialisation de la destination

    destination ← arbre


    étape 2 : on explore l'arbre jusqu'à trouver une destination vide

    TANT QUE NON estABV(destination)

      arbre_parent ← destination    # on se déplace jusqu'à la destination

      SI cle(noeud) < cle(racine(arbre_parent))

        destination ← gauche(arbre_parent)

      SINON

        destination ← droite(arbre_parent)

      Fin SI

    Fin Tant Que


    étape 3 : nd devient un sous-arbre de arbre_parent

    SI cle(nd) < cle(racine(arbre_parent))

      inserer_gauche(arbre_parent, noeud)

    SINON

      inserer_droite(arbre_parent, noeud)

    Fin SI

    Renvoyer VIDE

07° Quels sont les coûts des étapes 1, 2 et 3 ? Quel est le coût de l'insertion d'un nouveau noeud dans un ABR (par rapport à la hauteur de l'ABR) ?

...CORRECTION...

Etape 1 : Coût constant 𝓞(1).

Etape 2 : Coût linéaire en fonction de la hauteur h de l'arbre 𝓞(h).

Etape 3 : Coût constant 𝓞(1).

Au total, l'insertion est donc LINEAIRE par rapport à la hauteur h de l'ABR.

08° Exécuter l'algorithme pour insérer 31 dans cet Arbre :

Que contiennent les clés des racines de arbre_parent et destination à chaque tour dans la boucle TANT QUE puis à la fin de l'algorithme ?

Visualisation du site usfca.edu

...CORRECTION...

1er tour de boucle :

  • arbre_parent possède la clé 33
  • destination possède la clé 16

2e tour de boucle :

  • arbre_parent possède la clé 16
  • destination possède la clé 32

3e tour de boucle :

  • arbre_parent possède la clé 32
  • destinationest un ABV.

On sort donc de la boucle.

A la fin des boucles, on voit donc qu'on va insérer le nouveau noeud sur le noeud-parent 32 puisque arbre_parent possède la clé 32.

09° Retrouver l'algorithme inserer_noeud_dans_ABR() permettant d'insérer un noeud sans regarder vos notes.

2.4 Coût de l'algorithme d'insertion d'un noeud dans un ABR (sans optimisation)

C'est comme pour la recherche.

Le coût est linéaire par rapport à la hauteur h l'Arbre Binaire : 𝓞(h).

  1. Si l'AB est parfait, on obtient un coût logarithmique sur la taille de l'Arbre : 𝓞(log2(n))
  2. Si l'AB est filiforme, on obtient un coût linéaire par rapport à la taille : 𝓞(n)
  3. Si l'AB est quelconque, on est entre les deux et donc 𝓞(n)

9B° Trouver l'algorithme récursif inserer_noeud_dans_ABR(). Commencez par réflechir aux cas de base, ceux où on sait qu'on peut insérer.

3 - Algorithme de recherche

⇩ ⇧ ⤊

L'Arbre Binaire de Recherche permet de faire des recherches ciblées et donc de permettre des recherches à coût logarithmique.

3.1 Coût d'une recherche dans un ABR

Le coût est linéaire par rapport à la hauteur h l'Arbre Binaire : 𝓞(h).

  1. Si l'AB est parfait, on obtient un coût logarithmique sur la taille de l'Arbre : 𝓞(log2(n))
  2. Si l'AB est filiforme, on obtient un coût linéaire par rapport à la taille : 𝓞(n)
  3. Si l'AB est quelconque, on est entre les deux et donc 𝓞(n)

10° Proposer un algorithme permettant de rechercher un noeud dans un ABR.

On travaillera à partir des indications ci-dessous :

Dans un Arbre Binaire de Recherche (ABR), la recherche d'une clé cr est ciblée : il suffit de comparer la valeur de la clé cr cherchée et la valeur de la clé c du noeud actuel pour savoir où aller ensuite.

Inutile donc de faire une recherche linéaire en profondeur ou en largeur : on utilise ces méthodes d'exploration lorsqu'on ne sait pas où chercher justement.

  1. Si l'arbre actuel est un arbre vide, on renvoie un ABV.
  2. Si c'est la bonne clé (cr == c), on a trouvé. On renvoie alors l'ABR dont la racine est ce noeud.
  3. Si la clé cherchée est plus petite que la clé du noeud (cr < c): arbre devient le sous-arbre de gauche.
  4. Si la clé cherchée est plus grande que la clé du noeud (cr > c): arbre devient le sous-arbre de droite.

Algorithme de recherche

ENTREE 1 : un Arbre Binaire de Recherche arbre

ENTREE 2 : une Clé cr

SORTIE : un AB qui est soit la référence d'un ABR portant cette clé ou un ABV.

recherche(arbre:ABR, cr:Cle) -> ABR

A vous d'agir !

Voici la correction :

3.2 Algorithme (itératif, 2 sorties) de recherche dans un ABR

Principe

La recherche d'une clé cr est ciblée :

  1. Si l'arbre actuel est un arbre vide, on renvoie cet arbre VIDE.
  2. Si c'est la bonne clé (cr == c), on a trouvé. On renvoie l'ABR dont la racine porte cette clé.
  3. Si la clé cherchée est plus petite que la clé du noeud actuel, on va à gauche.
  4. Si la clé cherchée est plus grande que la clé du noeud actuel, on va à droite.
Description des entrées

ENTREE 1 : un ABR arbre

ENTREE 2 : une clé cr

SORTIE : la référence d'un ABR portant cette clé, potentiellement un ABV.

Description de l'algorithme

recherche(arbre:ABR, cr:Cle) -> ABR

    TANT QUE NON estABV(arbre)

      SI cr == cle(racine(arbre))

        Renvoyer arbre

      SINON SI cr < cle(racine(arbre))

        arbre ← gauche(arbre)

      SINON SI cr > cle(racine(arbre))

        arbre ← droite(arbre)

      Fin SI

    Fin Tant Que

    Renvoyer arbre # C'est un ABV si on arrive ici

11° Appliquer cet algorithme sur cet arbre en cherchant 22.

ABR complet

12° Dans le pire des cas, quel est le coût de cet algortihme en fonction de la hauteur de l'arbre ? En fonction de la taille pour un arbre complet ?

ABR complet

...CORRECTION...

On retrouve un coût linéaire par rapport à la hauteur.

Pour un arbre complet, le coût est donc logarithmique base 2 par rapport à la taille puisqu'à chaque étape, on réduit approximativement par deux le nombre de noeuds à supprimer de la recherche.

Il existe bien d'autres façon de gérer un algorithme de recherche dans un ABR.

13° Proposer une version de l'algorithme de recherche possédant un unique return. Cela permet de réaliser la preuve de correction plus facilement. Dans le cas présenté, on a une boucle non bornée TANT QUE qui va s'arrêter non pas à cause de sa condition d'arrêt propre mais à cause du retour qui provoque la sortie de l'algorithme ! Pas très propre...

recherche(arbre:ABR, cr:Cle) -> ABR

Voici la correction :

3.3 Algorithme (itératif, 1 sortie) de recherche dans un ABR

Description des entrées

ENTREE 1 : un ABR arbre

ENTREE 2 : une clé cr

SORTIE : la référence d'un ABR portant la clé, potentiellement un ABV.

Description de l'algorithme

recherche(arbre:ABR, cr:Cle) -> ABR

    reponse ← ABV

    TANT QUE NON estABV(arbre)

      SI cr == cle(racine(arbre))

        reponse ← arbre

        arbre ← ABV

      SINON SI cr < cle(racine(arbre))

        arbre ← gauche(arbre)

      SINON SI cr > cle(racine(arbre))

        arbre ← droite(arbre)

      Fin SI

    Fin Tant Que

    Renvoyer reponse

14° Proposer une version utilisant la récursivité. Pour cela, demandez-vous quels sont les cas de base, et ce qu'il faut faire sur les cas récursifs.

Dans cette version, arbre pourra être un arbre vide.

3.4 Algorithme (récursif) de recherche dans un ABR

Description des entrées

ENTREE 1 : un ABR arbre

ENTREE 2 : une clé cr

SORTIE : la référence d'un ABR portant la clé, potentiellement un ABV.

Description de l'algorithme

recherche(arbre:ABR, cr:Cle) -> ABR

      SI estABV(arbre)

        Renvoyer arbre

      SINON SI cr == cle(racine(arbre))

        Renvoyer arbre

      SINON SI cr < cle(racine(arbre))

        Renvoyer recherche(gauche(arbre), cr)

      SINON SI cr > cle(racine(arbre))

        Renvoyer recherche(droite(arbre), cr)

      Fin SI

3.5 AB équilibré

ABR Parfait, ABR Complet : coût logarithmique en recherche

Vous savez qu'un ABR est parfait si le dernier étage est entièrement rempli par les feuilles de l'arbre.

ABR complet

Dans un ABR parfait, le coût de l'insertion et de la recherche est alors 𝓞(log2(n)).

Or, ce cas est assez rare : il faut déjà que le nombre de noeuds soit exactement n = 2x - 1.

Si l'ABR est complet, il manque uniquement quelques feuille sur le dernier étage mais l'arbre est sinon rempli. Le coût asymptotique des algorithmes reste donc équivalent à celui de l'arbre parfait : 𝓞(log2(n)).

ABR équilibré ou AVL : coût logarithmique également

Nous allons rajouter une nouvelle variante d'ABR beaucoup plus courant mais dont le coût est globalement comparable à celui d'un AB parfait ou d'un AB complet : l'AB équilibré.

La notion d'arbre équilibré possède plusieurs variantes. Nous allons en voir une qui date de 1962. Deux mathématiciens, Adel'son-Vel'skii et Landis, introduisent des critères définissant un équilibre. Les arbres vérifiant ces critères sont connus sous le nom d'arbres AVL. Avec ce critère AVL, un arbre équilibré est un arbre pour lequel, pour tout nœud de l'arbre, la différence entre les hauteurs de ses deux sous-arbres ne peut excéder 1.

Exemples

Pour les exemples ci-dessous, le choix de la convention n'a aucune importance. J'ai choisi d'utiliser pR = 0, mais pR = 1 aurait donner les mêmes résultats.

Exemple 1 : Cet Arbre n'est pas un Arbre Binaire équilibré AVL : le noeud 17 possède à gauche un sous-arbre de hauteur 1 et à droite un sous-arbre de hauteur -1 (un arbre vide)

ABR pas équilibré

Exemple 2 : Par contre, cet Arbre est un Arbre Binaire équilibré :

ABR équilibré
Intérêt de la notion d'arbre équilibré ?

Cette définition va permettre d'étendre formellement le coût logarithmique d'une recherche ou d'une insertion (𝓞(log2(n))) à une gamme d'ABR non réellement parfaits.

4 - FAQ

⇩ ⇧ ⤊

Rien pour le moment

La dernière activité traite de l'implémentation Python des algorithmes sur l'Arbre Binaire de Recherche.

Activité publiée le 02 01 2021
Dernière modification : 30 01 2021
Auteur : ows. h.


⏪

⏫

⏩