1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
| """Module implémentant un Arbre Binaire (AB) avec un modèle objet
"""
# Déclaration de la classe AB
class AB:
"""Implémentation d'un Arbre Binaire"""
def __init__(self, valeur, gauche, droite):
self.v = valeur
self.g = gauche
self.d = droite
def relier_a_gauche(self:'AB NON VIDE', sous_arbre:'AB'):
"""Méthode qui définit sous_arbre comme le sous-arbre gauche de l'arbre actif"""
self.g = sous_arbre
def relier_a_droite(self:'AB NON VIDE', sous_arbre:'AB'):
"""Méthode qui définit sous_arbre comme le sous-arbre droite de l'arbre actif"""
self.d = sous_arbre
def definir_donnees_racine(self:'AB', element:'Element NON VIDE'):
"""Méthode qui place l'élément NON VIDE en tant que racine de l'arbre"""
self.v = element
def vider(self:'AB'):
"""Méthode qui transforme l'arbre en AB VIDE"""
self.v = None
self.g = None
self.d = None
# Fonctions d'interface (accessibles de l'extérieur)
def contenu(noeud:'Noeud') -> 'Element':
"""Renvoie le contenu associé au noeud fourni"""
return noeud.v
def nv_ABV() -> 'AB VIDE':
"""Renvoie un nouvel Arbre Binaire Vide"""
return AB(None, None, None)
def nv_AB(valeur:'Element', g:'AB', d:'AB') -> 'AB NON VIDE':
"""Renvoie un nouvel Arbre Binaire dont la racine porte valeur et qui mène aux sous-arbres g et d"""
return AB(valeur, g, d)
def est_ABV(arbre:'AB') -> bool:
"""Prédicat qui renvoie True si l'arbre est vide"""
return arbre.v is None and arbre.g is None and arbre.d is None
def racine(arbre:'AB NON VIDE') -> 'Noeud':
"""Renvoie le noeud-racine de l'Arbre Binaire NON VIDE"""
return arbre # ici arbre et racine sont des alias
def gauche(arbre:'AB NON VIDE') -> 'AB':
"""Renvoie le sous-arbre gauche de l'Arbre Binaire NON VIDE"""
return arbre.g
def droite(arbre:'AB NON VIDE') -> 'AB':
"""Renvoie le sous-arbre droite de l'Arbre Binaire NON VIDE"""
return arbre.d
# Programme de test du module
if __name__ == "__main__":
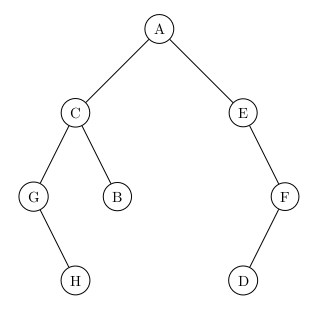
ad = nv_AB("D", nv_ABV(), nv_ABV())
af = nv_AB("F", ad, nv_ABV())
ae = nv_AB("E", nv_ABV(), af)
ah = nv_AB("H", nv_ABV(), nv_ABV())
ag = nv_AB("G", nv_ABV(), ah)
ab = nv_AB("B", nv_ABV(), nv_ABV())
ac = nv_AB("C", ag, ab)
aa = nv_AB("A", ac, ae)
print(contenu(racine(gauche(aa))))
|