14 - knn le retour
Nous allons poursuivre sur l'étude de l'algorithme des k plus proches voisins, knn.
Pourquoi knn ? Pour k-nearest neighbors algorithm.
Logiciel nécessaire pour l'activité : Python 3 : Thonny, IDLE ou le site repl.it ...
Prérequis : Algorithmes : knn
Evaluation ✎ : question 07
Documents de cours :
1 - Rappel rapide sur le knn
Le principe global des knn est de calculer les distances entre les différents enregistrements et un enregistrement dont on ne connaît pas la catégorie.
On attribue alors à l'enregistrement inconnu la catégorie la plus courante parmi les k plus proches voisins.
Nous avions décomposé l'algorithme en 4 parties (et réalisé les deux premières avec Python) :
- Etape 1 (réalisée en Python)
- Stocker les distances de k premiers enregistrements dans un tableau memoire
- Trier les k enregistrements dans memoire en fonction de la distance
- Etape 2 (réalisée en Python)
- Pour chaque enregistrement restant :
- calculer la distance
- si cette distance est plus petite que la plus grande des distances mémorisées : remplacer la plus grande par la nouvelle et trier à nouveau le tableau memoire
- Etape 3 (réalisée à la main)
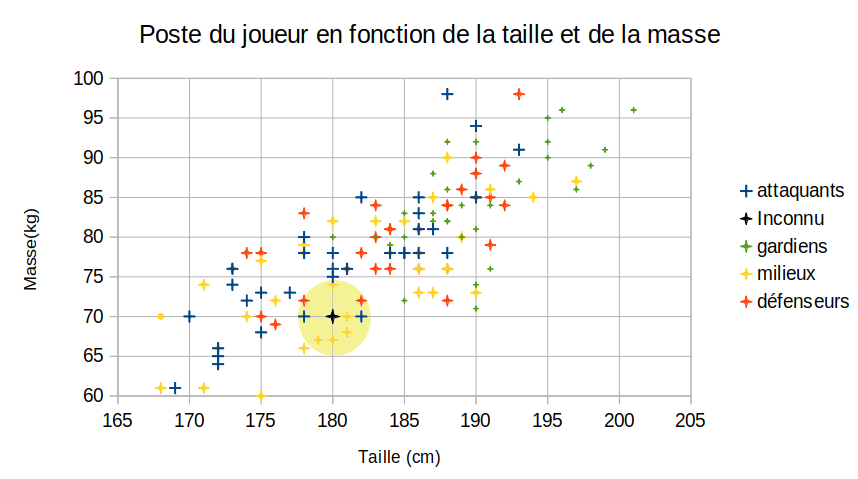
- On compte les catégories présentes dans le tableau memoire (ici, il s'agit des 9 enregistrements présents dans le cercle jaune)
- Etape 4 (réalisée à la main)
- On renvoie la catégorie la plus présente (ici les violets, soit les milieux de terrain)
⚐ Etape 1 ➡ ajout de k couples (distance, catégorie) dans memoire
memoire ← Tableau vide ayant longueur éléments
index ← 0
TANT QUE index < k
d ← distance (nouveau, collection[index])
on calcule la distance entre les deux enregistrements
categorie ← collection[index]['Poste']
on récupère la catégorie de l'enregistrement via la clé 'Poste'
memoire[index] ← (d, categorie)
on mémorise un couple (p-uplet) contenant distance et catégorie
index ← index + 1
on avance dans la lecture de la collection
Fin du TANT QUE
trie(memoire) en ordre croissant de distance (l'index 0)
laPlusGrande ← memoire[k-1][0]
⚐ Etape 2 ➡ on lit la suite mais on ne mémorise que si la distance est plus petite que l'une des précédentes
TANT QUE index < longueur de la collection
d ← distance (nouveau, collection[index])
On calcule la distance entre les deux enregistrements
SI d < laPlusGrande en mémoire
categorie ← collection[index]['Poste']
On récupère la catégorie de l'enregistrement
memoire[k-1] ← (d, categorie)
On place le couple (distance,catégorie) en mémoire en dernière position
trie(memoire) en ordre croissant de distance (l'index 0)
laPlusGrande ← memoire[k-1][0]
Fin du SI
index ← index + 1
Fin du TANT QUE
⚐ Etape 3 ➡ on compte les catégories présentes
nombres ← Dictionnaire vide
index ← 0
TANT QUE index < k
categorie ← memoire[index][1]
SI la clé categorie existe déjà dans le dictionnaire nombres
nombres[categorie] ← nombres[categorie] + 1
SINON
nombres[categorie] ← 1
Fin du SI
Fin TANT QUE
⚐ Etape 4 : on renvoie la catégorie majoritaire
reponse ← cleMajoritaire(nombres)
Renvoyer reponse
2 - Téléchargement des ressources
01° Créer un dossier nommé knn3 sur votre poste. Créer un fichier Python nommé recuperation.py contenant ce code
1
2
3
4
5 | import urllib.request
urllib.request.urlretrieve('https://doc.infoforall.fr/activite/algo/cours/knn/creation_collection.py', 'creation_collection.py')
urllib.request.urlretrieve('https://doc.infoforall.fr/activite/algo/cours/knn/entrainement.csv', 'entrainement.csv')
urllib.request.urlretrieve('https://doc.infoforall.fr/activite/algo/cours/knn/test.csv', 'test.csv')
urllib.request.urlretrieve('https://doc.infoforall.fr/activite/algo/cours/knn/gestion_finale.py', 'gestion.py')
|
La fonction urlretrieve du module request contenu dans urllib permet de créer un téléchargement en fournissant l'URL voulue et le nom sous lequel on veut enregistrer le téléchargement.
Lancer le code. Vous devriez obtenir un dossier contenant les 5 fichiers suivants :
Si ce n'est pas le cas, il est temps de créer cette structure et de télécharger les fichiers (clic-droit, télécharger sous).
Voici le contenu du programme gestion.py qui gère complétement knn.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85 | # 1 - Importation
from creation_collection import creer_collection
from matplotlib import pyplot as plt
from math import sqrt
from operator import itemgetter
# 2 - Déclaration des fonctions
def distance(enr1, enr2):
"""Fonction qui renvoie la distance entre les deux enregistrements
:: param enr1 (dict) :: un dictionnaire correspondant à un enregistrement
:: param enr2 (dict) :: un dictionnaire correspondant à un enregistrement
:: return (float) :: la distance euclidienne entre les deux enregistrements
"""
x1 = enr1['Taille (cm)']
x2 = enr2['Taille (cm)']
y1 = enr1['Masse (kg)']
y2 = enr2['Masse (kg)']
d = sqrt( (x2-x1)**2 + (y2-y1)**2 )
return d
def knn(k, nouveau, collection):
"""Fonction qui renvoie la catégorie supposée de nouveau
:: param k(int) :: le nombre de plus proches voisins à gérer
:: param nouveau(dict) :: un enregistrement sans connaissance de la clé de catégorie
:: param collection(list) :: une collection d'enregistrements
:: return (tuple) :: un tuple contenant la ou les catégories majoritaires
"""
# Etape 1 - ajout de k couples (distance, catégorie) dans memoire
memoire = []
for index in range(k):
d = distance(nouveau, collection[index])
categorie = collection[index]['Poste']
memoire.append( (d,categorie) )
memoire.sort(key=itemgetter(0))
laPlusGrande = memoire[k-1][0]
# Etape 2 - on rajoute les autres au cas par cas
for index in range(k, len(collection)):
d = distance(nouveau, collection[index])
if d < laPlusGrande:
categorie = collection[index]['Poste']
memoire[k-1] = (d,categorie)
memoire.sort(key=itemgetter(0))
laPlusGrande = memoire[k-1][0]
# Etape 3 - on compte les catégories présentes dans memoire
nombres = {}
for enregistrement in memoire:
categorie = enregistrement[1]
if categorie in nombres:
nombres[categorie] = nombres[categorie] + 1
else:
nombres[categorie] = 1
# Etape 4 - on cherche la catégorie majoritaire
reponse = None
maximum = 0
for cle, valeur in nombres.items():
if valeur > maximum:
reponse = (cle,)
maximum = valeur
elif valeur == maximum:
reponse = reponse + (cle,)
return reponse
# 3 - Programme
if __name__ == '__main__':
# Collection : Création de la collection
joueurs = creer_collection("entrainement.csv")
# Collection : transformation en entiers des descripteurs numériques
for index in range(len(joueurs)):
joueurs[index]['Taille (cm)'] = int(joueurs[index]['Taille (cm)'])
joueurs[index]['Masse (kg)'] = int(joueurs[index]['Masse (kg)'])
enr_test = {'Poste':'X', 'Taille (cm)':182, 'Masse (kg)':75}
|
02° Lancer le programme gestion.py.
Taper les instructions suivantes pour vérifier qu'il répond bien :
>>> joueurs[0]
{'Poste': 'Attaquant', 'Taille (cm)': 178, 'Masse (kg)': 80}
Cela permet de vérifier que les enregistrements contenus dans notre collection-tableau joueurs sont des dictionnaires.
>>> knn(3, enr_test, joueurs)
('Défenseur',)
3 - Evaluer la pertinence des réponses
Pour l'instant, nous n'avons travaillé qu'avec les données du fichier CSV entrainement.csv.
Nous allons maintenant comparer les postes des joueurs dans test.csv avec la catégorie que knn leur attribue.
Les seules modifications se trouvent dans le corps du programme, après la ligne 73.
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87 |
# 3 - Programme
if __name__ == '__main__':
# Collection : Création des collections
joueurs = creer_collection("entrainement.csv")
jeu_test = creer_collection("test.csv")
# Collection : transformation en entiers des descripteurs numériques
for index in range(len(joueurs)):
joueurs[index]['Taille (cm)'] = int(joueurs[index]['Taille (cm)'])
joueurs[index]['Masse (kg)'] = int(joueurs[index]['Masse (kg)'])
for index in range(len(jeu_test)):
jeu_test[index]['Taille (cm)'] = int(jeu_test[index]['Taille (cm)'])
jeu_test[index]['Masse (kg)'] = int(jeu_test[index]['Masse (kg)'])
|
03° Comment se nomme la collection qui contient les joueurs qui vont permettre de réaliser le test : joueurs ou jeu_test ?
Lancer le programme en utilisant maintenant la partie ci-dessous en tant que programme principal. Cela mettra les deux collections en mémoire.
Utilisez la console pour :
- Obtenir le nombre d'enregistrements dans le jeu de tests
- Visualiser les deux premiers enregistrements du jeu de tests
...CORRECTION...
>>> len(jeu_test)
32
>>> jeu_test[0]
{'Poste': 'Attaquant', 'Taille (cm)': 170, 'Masse (kg)': 70}
>>> jeu_test[1]
{'Poste': 'Attaquant', 'Taille (cm)': 185, 'Masse (kg)': 78}
Pour tester l'algorithme, nous allons simplement lui demander de fournir la réponse attendue pour les différents joueurs enregistrés dans la collection du jeu de tests : voir les lignes 89 à 93.
73
74
75
76
77
78
79
80
81
82
83
83
84
85
86
87
88
89
90
91
92
93 | # 3 - Programme
if __name__ == '__main__':
# Collection : Création des collections
joueurs = creer_collection("entrainement.csv")
jeu_test = creer_collection("test.csv")
# Collection : transformation en entiers des descripteurs numériques
for index in range(len(joueurs)):
joueurs[index]['Taille (cm)'] = int(joueurs[index]['Taille (cm)'])
joueurs[index]['Masse (kg)'] = int(joueurs[index]['Masse (kg)'])
for index in range(len(jeu_test)):
jeu_test[index]['Taille (cm)'] = int(jeu_test[index]['Taille (cm)'])
jeu_test[index]['Masse (kg)'] = int(jeu_test[index]['Masse (kg)'])
# Lancement des essais de validation
k = 5
for joueur in jeu_test:
poste_knn = knn(k, joueur, joueurs)
poste_reel = joueur['Poste']
print(f"Pour un joueur {poste_reel}, on obtient cette réponse {poste_knn}")
|
04° Lancer le programme en utilisant le code ci-dessus pour la partie principale.
L'algorithme knn donne-t-il toujours la bonne réponse ?
...CORRECTION...
Pour un joueur Attaquant, on obtient cette réponse ('Attaquant',)
Pour un joueur Attaquant, on obtient cette réponse ('Attaquant',)
Pour un joueur Attaquant, on obtient cette réponse ('Défenseur', 'Attaquant')
Pour un joueur Attaquant, on obtient cette réponse ('Gardien',)
Pour un joueur Attaquant, on obtient cette réponse ('Gardien',)
Pour un joueur Attaquant, on obtient cette réponse ('Attaquant',)
Pour un joueur Attaquant, on obtient cette réponse ('Attaquant',)
Pour un joueur Attaquant, on obtient cette réponse ('Attaquant',)
Pour un joueur Défenseur, on obtient cette réponse ('Attaquant',)
Pour un joueur Défenseur, on obtient cette réponse ('Attaquant',)
Pour un joueur Défenseur, on obtient cette réponse ('Gardien', 'Défenseur')
Pour un joueur Défenseur, on obtient cette réponse ('Défenseur',)
Pour un joueur Défenseur, on obtient cette réponse ('Attaquant',)
Pour un joueur Défenseur, on obtient cette réponse ('Défenseur', 'Milieu de terrain')
Pour un joueur Défenseur, on obtient cette réponse ('Gardien',)
Pour un joueur Défenseur, on obtient cette réponse ('Défenseur',)
Pour un joueur Gardien, on obtient cette réponse ('Défenseur',)
Pour un joueur Gardien, on obtient cette réponse ('Défenseur', 'Gardien')
Pour un joueur Gardien, on obtient cette réponse ('Attaquant', 'Défenseur')
Pour un joueur Gardien, on obtient cette réponse ('Attaquant',)
Pour un joueur Gardien, on obtient cette réponse ('Défenseur', 'Gardien')
Pour un joueur Gardien, on obtient cette réponse ('Gardien',)
Pour un joueur Gardien, on obtient cette réponse ('Gardien', 'Défenseur')
Pour un joueur Gardien, on obtient cette réponse ('Défenseur', 'Milieu de terrain')
Pour un joueur Milieu de terrain, on obtient cette réponse ('Défenseur', 'Milieu de terrain')
Pour un joueur Milieu de terrain, on obtient cette réponse ('Milieu de terrain', 'Défenseur')
Pour un joueur Milieu de terrain, on obtient cette réponse ('Attaquant',)
Pour un joueur Milieu de terrain, on obtient cette réponse ('Attaquant',)
Pour un joueur Milieu de terrain, on obtient cette réponse ('Attaquant',)
Pour un joueur Milieu de terrain, on obtient cette réponse ('Attaquant',)
Pour un joueur Milieu de terrain, on obtient cette réponse ('Attaquant',)
Pour un joueur Milieu de terrain, on obtient cette réponse ('Attaquant',)
On constate donc que l'algorithme fournit assez souvent une valeur qui ne correspond pas à la vraie catégorie.
L'algorithme n'est donc pas magique : il se trompe. C'est normal : les réponses d'un programme de décision sont toujours fournies avec une certaine marge d'erreur : comprendre que la réponse attendue n'est pas une certitude est fondamentale lorqu'on étudie les réponses de l'ordinateur.
Mais l'ordinateur donne-t-il plus souvent une bonne réponse que quelqu'un qui répondrait au hasard (4 catégories, 25 % de chances).
Pour le savoir, nous allons maintenant comparer les réponses de notre fonction knn et créer trois compteurs :
89
90
91
92
93 | # Lancement des essais de validation
k = 1
unique = 0
double = 0
faux = 0
|
Nous allons ensuite lancer le knn sur chaque enregistrement joueur de la collection jeu_test.
94
95 | for joueur in jeu_test:
reponse = knn(k,joueur, joueurs)
|
Il ne reste plus ensuite qu'à incrémenter les compteurs en comparant le tuple de réponse à la vraie réponse, puisqu'on connait la catégorie des joueurs contenu dans le jeu de tests.
- Le compteur unique mémorise le nombre de fois où l'ordinateur répond bien par une seule catégorie et qu'elle est bien celle enregistrée pour ce joueur.
- Le compteur double mémorise le nombre de fois où l'ordinateur répond par deux catégories et que l'une des deux est la bonne.
- Le compteur faux mémorise le nombre de fois où l'ordinateur fournit une réponse qui ne contient pas du tout la catégorie du joueur.
96
97 | if len(reponse) == 1 and joueur['Poste'] == reponse[0]:
unique = unique + 1
|
98
99 | elif len(reponse) == 2 and joueur['Poste'] in reponse:
double = double + 1
|
100
101 | else:
faux = faux + 1
|
Il ne reste plus qu'à présenter le résultat une fois qu'on sort de la boucle.
103 | print(f"Pour k = {k}, on obtient {unique} bonnes réponses uniques, {double} réponses doubles et {faux} fausses réponses")
|
05° Lancer le programme complet ci-dessous qui gère les comptes.
Modifier le pour savoir s'il donne de meilleurs résultats pour k=1, k=3 ou k=5.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103 | # 1 - Importation
from creation_collection import creer_collection
from matplotlib import pyplot as plt
from math import sqrt
from operator import itemgetter
# 2 - Déclaration des fonctions
def distance(enr1, enr2):
"""Fonction qui renvoie la distance entre les deux enregistrements
:: param enr1 (dict) :: un dictionnaire correspondant à un enregistrement
:: param enr2 (dict) :: un dictionnaire correspondant à un enregistrement
:: return (float) :: la distance euclidienne entre les deux enregistrements
"""
x1 = enr1['Taille (cm)']
x2 = enr2['Taille (cm)']
y1 = enr1['Masse (kg)']
y2 = enr2['Masse (kg)']
d = sqrt( (x2-x1)**2 + (y2-y1)**2 )
return d
def knn(k, nouveau, collection):
"""Fonction qui renvoie la catégorie supposée de nouveau
:: param k(int) :: le nombre de plus proches voisins à gérer
:: param nouveau(dict) :: un enregistrement sans connaissance de la clé de catégorie
:: param collection(list) :: une collection d'enregistrements
:: return (tuple) :: un tuple contenant la ou les catégories majoritaires
"""
# Etape 1 - ajout de k couples (distance, catégorie) dans memoire
memoire = []
for index in range(k):
d = distance(nouveau, collection[index])
categorie = collection[index]['Poste']
memoire.append( (d,categorie) )
memoire.sort(key=itemgetter(0))
laPlusGrande = memoire[k-1][0]
# Etape 2 - on rajoute les autres au cas par cas
for index in range(k, len(collection)):
d = distance(nouveau, collection[index])
if d < laPlusGrande:
categorie = collection[index]['Poste']
memoire[k-1] = (d,categorie)
memoire.sort(key=itemgetter(0))
laPlusGrande = memoire[k-1][0]
# Etape 3 - on compte les catégories présentes dans memoire
nombres = {}
for enregistrement in memoire:
categorie = enregistrement[1]
if categorie in nombres:
nombres[categorie] = nombres[categorie] + 1
else:
nombres[categorie] = 1
# Etape 4 - on cherche la catégorie majoritaire
reponse = None
maximum = 0
for cle, valeur in nombres.items():
if valeur > maximum:
reponse = (cle,)
maximum = valeur
elif valeur == maximum:
reponse = reponse + (cle,)
return reponse
# 3 - Programme
if __name__ == '__main__':
# Collection : Création des collections
joueurs = creer_collection("entrainement.csv")
jeu_test = creer_collection("test.csv")
# Collection : transformation en entiers des descripteurs numériques
for index in range(len(joueurs)):
joueurs[index]['Taille (cm)'] = int(joueurs[index]['Taille (cm)'])
joueurs[index]['Masse (kg)'] = int(joueurs[index]['Masse (kg)'])
for index in range(len(jeu_test)):
jeu_test[index]['Taille (cm)'] = int(jeu_test[index]['Taille (cm)'])
jeu_test[index]['Masse (kg)'] = int(jeu_test[index]['Masse (kg)'])
# Lancement des essais de validation
k = 5
unique = 0
double = 0
faux = 0
for joueur in jeu_test:
reponse = knn(k,joueur, joueurs)
if len(reponse) == 1 and joueur['Poste'] == reponse[0]:
unique = unique + 1
elif len(reponse) == 2 and joueur['Poste'] in reponse:
double = double + 1
else:
faux = faux + 1
print(f"Pour k = {k}, on obtient {unique} bonnes réponses uniques, {double} réponses doubles et {faux} fausses réponses")
|
...CORRECTION...
Pour k = 1, on obtient 11 bonnes réponses uniques, 0 réponses doubles et 21 fausses réponsesPour k = 3, on obtient 10 bonnes réponses uniques, 0 réponses doubles et 22 fausses réponsesPour k = 5, on obtient 8 bonnes réponses uniques, 8 bonnes réponses et 16 fausses réponsesPas facile de voir cela avec des chiffres. Utilisons maintenant les pourcentages. J'ai juste modifié le code pour qu'il fournisse
- le pourcentage de bonnes réponses uniques,
- le pourcentage de bonnes réponses uniques ET doubles et
- le pourcentage de fausses réponses.
06° Lancer le programme complet ci-dessous qui gère les pourcentages. Sachant qu'on a 25% de chances de trouver la bonne réponse au hasard, l'algorithme des k plus proches voisins est-il pertinent pour trouver la catégorie d'un joueur en fonction uniquement de sa masse et de sa taille (faire le test avec k=1, k=3 et k=5) ?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106 | # 1 - Importation
from creation_collection import creer_collection
from matplotlib import pyplot as plt
from math import sqrt
from operator import itemgetter
# 2 - Déclaration des fonctions
def distance(enr1, enr2):
"""Fonction qui renvoie la distance entre les deux enregistrements
:: param enr1 (dict) :: un dictionnaire correspondant à un enregistrement
:: param enr2 (dict) :: un dictionnaire correspondant à un enregistrement
:: return (float) :: la distance euclidienne entre les deux enregistrements
"""
x1 = enr1['Taille (cm)']
x2 = enr2['Taille (cm)']
y1 = enr1['Masse (kg)']
y2 = enr2['Masse (kg)']
d = sqrt( (x2-x1)**2 + (y2-y1)**2 )
return d
def knn(k, nouveau, collection):
"""Fonction qui renvoie la catégorie supposée de nouveau
:: param k(int) :: le nombre de plus proches voisins à gérer
:: param nouveau(dict) :: un enregistrement sans connaissance de la clé de catégorie
:: param collection(list) :: une collection d'enregistrements
:: return (tuple) :: un tuple contenant la ou les catégories majoritaires
"""
# Etape 1 - ajout de k couples (distance, catégorie) dans memoire
memoire = []
for index in range(k):
d = distance(nouveau, collection[index])
categorie = collection[index]['Poste']
memoire.append( (d,categorie) )
memoire.sort(key=itemgetter(0))
laPlusGrande = memoire[k-1][0]
# Etape 2 - on rajoute les autres au cas par cas
for index in range(k, len(collection)):
d = distance(nouveau, collection[index])
if d < laPlusGrande:
categorie = collection[index]['Poste']
memoire[k-1] = (d,categorie)
memoire.sort(key=itemgetter(0))
laPlusGrande = memoire[k-1][0]
# Etape 3 - on compte les catégories présentes dans memoire
nombres = {}
for enregistrement in memoire:
categorie = enregistrement[1]
if categorie in nombres:
nombres[categorie] = nombres[categorie] + 1
else:
nombres[categorie] = 1
# Etape 4 - on cherche la catégorie majoritaire
reponse = None
maximum = 0
for cle, valeur in nombres.items():
if valeur > maximum:
reponse = (cle,)
maximum = valeur
elif valeur == maximum:
reponse = reponse + (cle,)
return reponse
# 3 - Programme
if __name__ == '__main__':
# Collection : Création des collections
joueurs = creer_collection("entrainement.csv")
jeu_test = creer_collection("test.csv")
# Collection : transformation en entiers des descripteurs numériques
for index in range(len(joueurs)):
joueurs[index]['Taille (cm)'] = int(joueurs[index]['Taille (cm)'])
joueurs[index]['Masse (kg)'] = int(joueurs[index]['Masse (kg)'])
for index in range(len(jeu_test)):
jeu_test[index]['Taille (cm)'] = int(jeu_test[index]['Taille (cm)'])
jeu_test[index]['Masse (kg)'] = int(jeu_test[index]['Masse (kg)'])
# Lancement des essais de validation
k = 5
unique = 0
double = 0
faux = 0
for joueur in jeu_test:
reponse = knn(k,joueur, joueurs)
if len(reponse) == 1 and joueur['Poste'] == reponse[0]:
unique = unique + 1
elif len(reponse) == 2 and joueur['Poste'] in reponse:
double = double + 1
else:
faux = faux + 1
simple_et_double = 100 / len(jeu_test) * (unique + double)
unique = 100 / len(jeu_test) * unique
faux = 100 / len(jeu_test) * faux
print(f"Pour k = {k:2}, {unique:.0f} % de bonnes réponses, {simple_et_double:.0f} % de simples et doubles, et {faux:.0f} % de fausses réponses")
|
...CORRECTION...
Pour k = 1, 34 % de bonnes réponses, 34 % de simples et doubles, et 66 % de fausses réponsesPour k = 3, 31 % de bonnes réponses, 31 % de simples et doubles, et 69 % de fausses réponsesPour k = 5, 25 % de bonnes réponses, 50 % de simples et doubles, et 50 % de fausses réponsesComme on peut le voir, nos résultats ne sont pas si bons que cela !
✎ 07° Modifier (et fournir sur la copie) le programme pour réaliser les tests en boucle pour k variant de 1 à 50.
Conclure sur la possibilité de classer les joueurs en fonction uniquement de la taille et de la masse.
Le résultat attendu :
Pour k = 1, 34 % de bonnes réponses, 34 % de simples et doubles, et 66 % de fausses réponses
Pour k = 2, 19 % de bonnes réponses, 56 % de simples et doubles, et 44 % de fausses réponses
Pour k = 3, 31 % de bonnes réponses, 31 % de simples et doubles, et 69 % de fausses réponses
Pour k = 4, 38 % de bonnes réponses, 41 % de simples et doubles, et 59 % de fausses réponses
Pour k = 5, 25 % de bonnes réponses, 50 % de simples et doubles, et 50 % de fausses réponses
Pour k = 6, 25 % de bonnes réponses, 31 % de simples et doubles, et 69 % de fausses réponses
Pour k = 7, 31 % de bonnes réponses, 38 % de simples et doubles, et 62 % de fausses réponses
Pour k = 8, 31 % de bonnes réponses, 47 % de simples et doubles, et 53 % de fausses réponses
Pour k = 9, 22 % de bonnes réponses, 47 % de simples et doubles, et 53 % de fausses réponses
Pour k = 10, 31 % de bonnes réponses, 38 % de simples et doubles, et 62 % de fausses réponses
Pour k = 11, 22 % de bonnes réponses, 34 % de simples et doubles, et 66 % de fausses réponses
Pour k = 12, 28 % de bonnes réponses, 34 % de simples et doubles, et 66 % de fausses réponses
Pour k = 13, 22 % de bonnes réponses, 41 % de simples et doubles, et 59 % de fausses réponses
Pour k = 14, 34 % de bonnes réponses, 38 % de simples et doubles, et 62 % de fausses réponses
Pour k = 15, 25 % de bonnes réponses, 41 % de simples et doubles, et 59 % de fausses réponses
Pour k = 16, 34 % de bonnes réponses, 41 % de simples et doubles, et 59 % de fausses réponses
Pour k = 17, 34 % de bonnes réponses, 47 % de simples et doubles, et 53 % de fausses réponses
Pour k = 18, 41 % de bonnes réponses, 41 % de simples et doubles, et 59 % de fausses réponses
Pour k = 19, 38 % de bonnes réponses, 44 % de simples et doubles, et 56 % de fausses réponses
Pour k = 20, 38 % de bonnes réponses, 44 % de simples et doubles, et 56 % de fausses réponses
Pour k = 21, 31 % de bonnes réponses, 38 % de simples et doubles, et 62 % de fausses réponses
Pour k = 22, 31 % de bonnes réponses, 34 % de simples et doubles, et 66 % de fausses réponses
Pour k = 23, 31 % de bonnes réponses, 34 % de simples et doubles, et 66 % de fausses réponses
Pour k = 24, 34 % de bonnes réponses, 41 % de simples et doubles, et 59 % de fausses réponses
Pour k = 25, 28 % de bonnes réponses, 44 % de simples et doubles, et 56 % de fausses réponses
Pour k = 26, 22 % de bonnes réponses, 38 % de simples et doubles, et 62 % de fausses réponses
Pour k = 27, 28 % de bonnes réponses, 38 % de simples et doubles, et 62 % de fausses réponses
Pour k = 28, 28 % de bonnes réponses, 34 % de simples et doubles, et 66 % de fausses réponses
Pour k = 29, 31 % de bonnes réponses, 31 % de simples et doubles, et 69 % de fausses réponses
Pour k = 30, 31 % de bonnes réponses, 31 % de simples et doubles, et 69 % de fausses réponses
Pour k = 31, 28 % de bonnes réponses, 31 % de simples et doubles, et 69 % de fausses réponses
Pour k = 32, 31 % de bonnes réponses, 34 % de simples et doubles, et 66 % de fausses réponses
Pour k = 33, 28 % de bonnes réponses, 34 % de simples et doubles, et 66 % de fausses réponses
Pour k = 34, 31 % de bonnes réponses, 31 % de simples et doubles, et 69 % de fausses réponses
Pour k = 35, 28 % de bonnes réponses, 31 % de simples et doubles, et 69 % de fausses réponses
Pour k = 36, 31 % de bonnes réponses, 38 % de simples et doubles, et 62 % de fausses réponses
Pour k = 37, 34 % de bonnes réponses, 34 % de simples et doubles, et 66 % de fausses réponses
Pour k = 38, 28 % de bonnes réponses, 38 % de simples et doubles, et 62 % de fausses réponses
Pour k = 39, 28 % de bonnes réponses, 34 % de simples et doubles, et 66 % de fausses réponses
Pour k = 40, 28 % de bonnes réponses, 28 % de simples et doubles, et 72 % de fausses réponses
Pour k = 41, 28 % de bonnes réponses, 34 % de simples et doubles, et 66 % de fausses réponses
Pour k = 42, 25 % de bonnes réponses, 34 % de simples et doubles, et 66 % de fausses réponses
Pour k = 43, 31 % de bonnes réponses, 41 % de simples et doubles, et 59 % de fausses réponses
Pour k = 44, 34 % de bonnes réponses, 44 % de simples et doubles, et 56 % de fausses réponses
Pour k = 45, 31 % de bonnes réponses, 41 % de simples et doubles, et 59 % de fausses réponses
Pour k = 46, 31 % de bonnes réponses, 44 % de simples et doubles, et 56 % de fausses réponses
Pour k = 47, 34 % de bonnes réponses, 41 % de simples et doubles, et 59 % de fausses réponses
Pour k = 48, 31 % de bonnes réponses, 41 % de simples et doubles, et 59 % de fausses réponses
Pour k = 49, 31 % de bonnes réponses, 41 % de simples et doubles, et 59 % de fausses réponses
Pour k = 50, 25 % de bonnes réponses, 44 % de simples et doubles, et 56 % de fausses réponses
On remarque que les meilleurs performances sur le jeu de tests sont obtenues autour de ces réglages :
Pour k = 17, 34 % de bonnes réponses, 47 % de simples et doubles, et 53 % de fausses réponses
Pour k = 18, 41 % de bonnes réponses, 41 % de simples et doubles, et 59 % de fausses réponses
Pour k = 19, 38 % de bonnes réponses, 44 % de simples et doubles, et 56 % de fausses réponses
Pour k = 20, 38 % de bonnes réponses, 44 % de simples et doubles, et 56 % de fausses réponses
S'il faut absolument utiliser cet algorithme sur ce problème, il serait donc judicieux d'utiliser l'une des ces valeurs. k = 19 semble un bon choix.
Mais bon, nous n'avons toujours que 38% de bonnes réponses en moyenne contre 25% au hasard. Pas fameux...
4 - Un peu de recul
Cette imprécision est tout à fait normal ici : les joueurs sont caractérisés par bien d'autres choses que la masse et la taille. Vitesse, précision, accélération, maîtrise du ballon...
Pourquoi avoir fait ce choix ici alors ? Pour vous montrer que ce n'est pas parce qu'un système informatique fournit une réponse qu'elle est pertinente. L'intelligence artificielle et les méthodes de décisions ne sont pas de la magie.
Qu'est-ce qui peut faire que l'algorithme des k plus proches voisins ne donne pas de résultats exploitables :
- Un biais dans les données initiales : trop d'enregistrements d'une catégorie, des enregistrements atypiques...
- Trop peu d'enregistrements
- Un problème où les catégories sont trop peu distinctes par rapport aux variables choisies (c'est le cas ici : dès le départ, on pouvait voir que les 4 catégories étaient très peu délimitées sur le graphique de base)
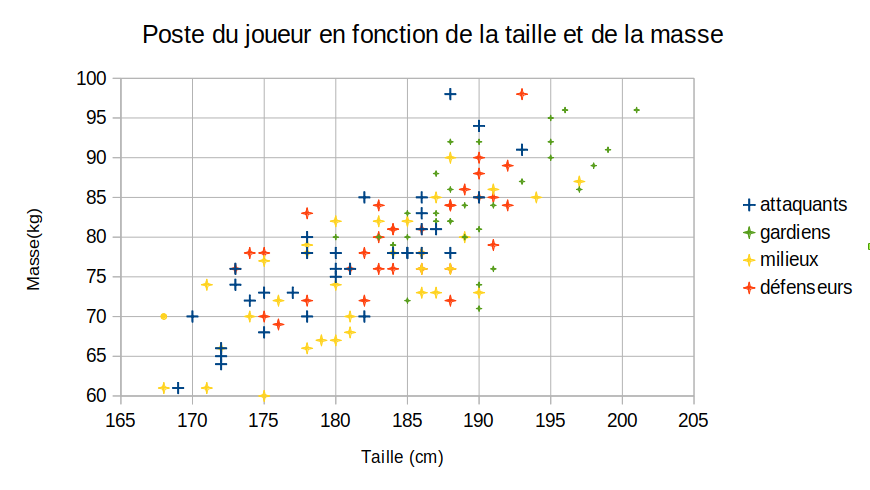
Rien qu'en voyant cela, on aurait pu savoir que les résultats n'allaient pas être très probants. Surtout qu'un même couple (taille,masse) peut être associé à plusieurs postes. Et surtout : qu'un même joueur peut changer de postes en cours de carrière.
Et donc, knn marche ou pas ?
Globalement, oui. Mais il faut savoir choisir les données à étudier et travailler sur un problème où les catégories sont vraiment liées aux variables initiales.
Il existe d'ailleurs deux façons d'utiliser notre algorithme :
- La classification : l'algortihme fournit une réponse parmi un ensemble de réponses prédéfinies : on tente de faire rentrer un enregistrement inconnu dans une catégorie précise comme avec nos joueurs.
- La régression : on tente par exemple de trouver la masse d'un joueur en connaissant sa taille et son poste.
Pour ne pas vous laisser sur votre faim, nous allons voir qu'il est également possible d'améliorer ou dégrader les performances en jouant sur le calcul de la distance. C'est en effet la pierre angulaire de tout le système.
08° Modifier la fonction distance de cette façon :
1
2
3
4
5
6
7
8
9
10
11
12
13
14 | def distance(enr1, enr2):
"""Fonction qui renvoie la distance entre les deux enregistrements
:: param enr1 (dict) :: un dictionnaire correspondant à un enregistrement
:: param enr2 (dict) :: un dictionnaire correspondant à un enregistrement
:: return (float) :: la distance euclidienne entre les deux enregistrements
"""
x1 = enr1['Taille (cm)']
x2 = enr2['Taille (cm)']
y1 = enr1['Masse (kg)'] * 0.66
y2 = enr2['Masse (kg)'] * 0.66
d = sqrt( (x2-x1)**2 + (y2-y1)**2 )
return d
|
On diminue donc la contribution de la masse au calcul de la distance.
Regardons les résultats :
Pour k = 1, 31 % de bonnes réponses, 31 % de simples et doubles, et 69 % de fausses réponses
Pour k = 2, 16 % de bonnes réponses, 56 % de simples et doubles, et 44 % de fausses réponses
Pour k = 3, 28 % de bonnes réponses, 28 % de simples et doubles, et 72 % de fausses réponses
Pour k = 4, 34 % de bonnes réponses, 38 % de simples et doubles, et 62 % de fausses réponses
Pour k = 5, 25 % de bonnes réponses, 44 % de simples et doubles, et 56 % de fausses réponses
Pour k = 6, 22 % de bonnes réponses, 28 % de simples et doubles, et 72 % de fausses réponses
Pour k = 7, 22 % de bonnes réponses, 25 % de simples et doubles, et 75 % de fausses réponses
Pour k = 8, 22 % de bonnes réponses, 31 % de simples et doubles, et 69 % de fausses réponses
Pour k = 9, 25 % de bonnes réponses, 34 % de simples et doubles, et 66 % de fausses réponses
Pour k = 10, 28 % de bonnes réponses, 38 % de simples et doubles, et 62 % de fausses réponses
Pour k = 11, 22 % de bonnes réponses, 31 % de simples et doubles, et 69 % de fausses réponses
Pour k = 12, 16 % de bonnes réponses, 34 % de simples et doubles, et 66 % de fausses réponses
Pour k = 13, 22 % de bonnes réponses, 34 % de simples et doubles, et 66 % de fausses réponses
Pour k = 14, 28 % de bonnes réponses, 34 % de simples et doubles, et 66 % de fausses réponses
Pour k = 15, 34 % de bonnes réponses, 41 % de simples et doubles, et 59 % de fausses réponses
Pour k = 16, 34 % de bonnes réponses, 44 % de simples et doubles, et 56 % de fausses réponses
Pour k = 17, 41 % de bonnes réponses, 44 % de simples et doubles, et 56 % de fausses réponses
Pour k = 18, 44 % de bonnes réponses, 44 % de simples et doubles, et 56 % de fausses réponses
Pour k = 19, 44 % de bonnes réponses, 44 % de simples et doubles, et 56 % de fausses réponses
Pour k = 20, 41 % de bonnes réponses, 44 % de simples et doubles, et 56 % de fausses réponses
Pour k = 21, 38 % de bonnes réponses, 41 % de simples et doubles, et 59 % de fausses réponses
Pour k = 22, 41 % de bonnes réponses, 44 % de simples et doubles, et 56 % de fausses réponses
Pour k = 23, 41 % de bonnes réponses, 41 % de simples et doubles, et 59 % de fausses réponses
Pour k = 24, 38 % de bonnes réponses, 50 % de simples et doubles, et 50 % de fausses réponses
Pour k = 25, 41 % de bonnes réponses, 44 % de simples et doubles, et 56 % de fausses réponses
Pour k = 26, 38 % de bonnes réponses, 50 % de simples et doubles, et 50 % de fausses réponses
Pour k = 27, 50 % de bonnes réponses, 50 % de simples et doubles, et 50 % de fausses réponses
Pour k = 28, 41 % de bonnes réponses, 53 % de simples et doubles, et 47 % de fausses réponses
Pour k = 29, 38 % de bonnes réponses, 41 % de simples et doubles, et 59 % de fausses réponses
Pour k = 30, 38 % de bonnes réponses, 41 % de simples et doubles, et 59 % de fausses réponses
Pour k = 31, 38 % de bonnes réponses, 38 % de simples et doubles, et 62 % de fausses réponses
Pour k = 32, 34 % de bonnes réponses, 38 % de simples et doubles, et 62 % de fausses réponses
Pour k = 33, 28 % de bonnes réponses, 38 % de simples et doubles, et 62 % de fausses réponses
Pour k = 34, 31 % de bonnes réponses, 34 % de simples et doubles, et 66 % de fausses réponses
Pour k = 35, 31 % de bonnes réponses, 31 % de simples et doubles, et 69 % de fausses réponses
Pour k = 36, 31 % de bonnes réponses, 34 % de simples et doubles, et 66 % de fausses réponses
Pour k = 37, 31 % de bonnes réponses, 34 % de simples et doubles, et 66 % de fausses réponses
Pour k = 38, 31 % de bonnes réponses, 31 % de simples et doubles, et 69 % de fausses réponses
Pour k = 39, 28 % de bonnes réponses, 31 % de simples et doubles, et 69 % de fausses réponses
Pour k = 40, 31 % de bonnes réponses, 34 % de simples et doubles, et 66 % de fausses réponses
Pour k = 41, 28 % de bonnes réponses, 31 % de simples et doubles, et 69 % de fausses réponses
Pour k = 42, 31 % de bonnes réponses, 38 % de simples et doubles, et 62 % de fausses réponses
Pour k = 43, 31 % de bonnes réponses, 34 % de simples et doubles, et 66 % de fausses réponses
Pour k = 44, 28 % de bonnes réponses, 34 % de simples et doubles, et 66 % de fausses réponses
Pour k = 45, 28 % de bonnes réponses, 34 % de simples et doubles, et 66 % de fausses réponses
Pour k = 46, 28 % de bonnes réponses, 34 % de simples et doubles, et 66 % de fausses réponses
Pour k = 47, 28 % de bonnes réponses, 34 % de simples et doubles, et 66 % de fausses réponses
Pour k = 48, 25 % de bonnes réponses, 31 % de simples et doubles, et 69 % de fausses réponses
Pour k = 49, 22 % de bonnes réponses, 28 % de simples et doubles, et 72 % de fausses réponses
Pour k = 50, 25 % de bonnes réponses, 34 % de simples et doubles, et 66 % de fausses réponses
Nous sommes parvenus à augmenter la réponse de quelques % pour k compris entre 17 et 20.
Pour k = 17, 41 % de bonnes réponses, 44 % de simples et doubles, et 56 % de fausses réponses
Pour k = 18, 44 % de bonnes réponses, 44 % de simples et doubles, et 56 % de fausses réponses
Pour k = 19, 44 % de bonnes réponses, 44 % de simples et doubles, et 56 % de fausses réponses
Pour k = 20, 41 % de bonnes réponses, 44 % de simples et doubles, et 56 % de fausses réponses
Attention néanmoins : notre échantillon de tests ne comporte que 32 joueurs. Modifier ainsi le calcul de la distance donne de bons résultats sur CE test. Mais le résultat est-il plus fiable sur n'importe quelle entrée ?
Comme vous le voyez, il y a encore bien des choses à dire sur cet algorithme...
Résumons
Algorithme knn des k plus proches voisins
knn pour k-nearest neighbors.
On considère qu'on dispose d'un ensemble d'enregistrements caractérisées par des attributs dont l'un peut servir par exemple de catégories de classement.
L'algorithme consiste à ne garder que les k plus proches voisins d'un enregistrement en regardant les k autres enregistrements les plus proches.
Habituellement
- Etape 1 : On calcule et stocke les k premières distances obtenues sur les premiers enregistrements.
- Etape 2 : On calcule la distance du prochain enregistrement et on ne l'insère dana la liste des k plus proches voisins que si sa distance est plus petites que l'une de celles qui sont mémorisées.
- Etape 3 : On compte les apparitions des différentes catégories parmi les k plus proches voisins.
 Etape 4 : On renvoie la ou les catégories les plus présentes.
Etape 4 : On renvoie la ou les catégories les plus présentes.
La façon dont on réalise le calcul de la distance ainsi que le nombre choisi pour k ont une influence sur les réponses de l'algorithme.
De façon à contrôler les résultats obtenus, on utilise une partie aléatoire des enregistrements connus de façon à avoir un jeu de tests permettant de connaitre les probabilités de bonnes réponses de notre algorithme.
Nous allons finir en fournissant simplement une façon de visualiser les résultats : je vais faire calculer à notre knn un ensemble d'enregistrements imaginaires comprenant toutes les coordonnées voulues.
Si l'algorithme répond par une réponse unique, je place un carré correspondant à la catégorie supposée par knn.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110 | # 1 - Importation
from creation_collection import creer_collection
from matplotlib import pyplot as plt
from math import sqrt
from operator import itemgetter
# 2 - Déclaration des fonctions
def distance(enr1, enr2):
"""Fonction qui renvoie la distance entre les deux enregistrements
:: param enr1 (dict) :: un dictionnaire correspondant à un enregistrement
:: param enr2 (dict) :: un dictionnaire correspondant à un enregistrement
:: return (float) :: la distance euclidienne entre les deux enregistrements
"""
x1 = enr1['Taille (cm)'] * 1
x2 = enr2['Taille (cm)'] * 1
y1 = enr1['Masse (kg)'] * 0.66
y2 = enr2['Masse (kg)'] * 0.66
d = sqrt( (x2-x1)**2 + (y2-y1)**2 )
return d
def knn(k, nouveau, collection):
"""Fonction qui renvoie la catégorie supposée de nouveau
:: param k(int) :: le nombre de plus proches voisins à gérer
:: param nouveau(dict) :: un enregistrement sans connaissance de la clé de catégorie
:: param collection(list) :: une collection d'enregistrements
:: return (tuple) :: un tuple contenant la ou les catégories majoritaires
"""
# Etape 1 - ajout de k couples (distance, catégorie) dans memoire
memoire = []
for index in range(k):
d = distance(nouveau, collection[index])
categorie = collection[index]['Poste']
memoire.append( (d,categorie) )
memoire.sort(key=itemgetter(0))
laPlusGrande = memoire[k-1][0]
# Etape 2 - on rajoute les autres au cas par cas
for index in range(k, len(collection)):
d = distance(nouveau, collection[index])
if d < laPlusGrande:
categorie = collection[index]['Poste']
memoire[k-1] = (d,categorie)
memoire.sort(key=itemgetter(0))
laPlusGrande = memoire[k-1][0]
# Etape 3 - on compte les catégories présentes dans memoire
nombres = {}
for enregistrement in memoire:
categorie = enregistrement[1]
if categorie in nombres:
nombres[categorie] = nombres[categorie] + 1
else:
nombres[categorie] = 1
# Etape 4 - on cherche la catégorie majoritaire
reponse = None
maximum = 0
for cle, valeur in nombres.items():
if valeur > maximum:
reponse = (cle,)
maximum = valeur
elif valeur == maximum:
reponse = reponse + (cle,)
return reponse
# 3 - Programme
if __name__ == '__main__':
# Collection : Création des collections
joueurs = creer_collection("entrainement.csv")
jeu_test = creer_collection("test.csv")
# Collection : transformation en entiers des descripteurs numériques
for index in range(len(joueurs)):
joueurs[index]['Taille (cm)'] = int(joueurs[index]['Taille (cm)'])
joueurs[index]['Masse (kg)'] = int(joueurs[index]['Masse (kg)'])
for index in range(len(jeu_test)):
jeu_test[index]['Taille (cm)'] = int(jeu_test[index]['Taille (cm)'])
jeu_test[index]['Masse (kg)'] = int(jeu_test[index]['Masse (kg)'])
# Création du graphique
k = 19
for taille in range(160, 206):
print(taille)
for masse in range(60,101):
joueur = {'Taille (cm)': taille, 'Masse (kg)': masse}
reponse = knn(k,joueur, joueurs)
if len(reponse) == 1:
if reponse[0] == 'Attaquant':
plt.plot(taille, masse, 'bs', label="Attaquants")
elif reponse[0] == 'Défenseur':
plt.plot(taille, masse, 'rs', label="Défenseurs")
elif reponse[0] == 'Milieu de terrain':
plt.plot(taille, masse, color='orange', marker='s',linewidth=0, label="Milieux de terrain")
elif reponse[0] == 'Gardien':
plt.plot(taille, masse, 'gs', label="Gardiens de but")
plt.xlabel("Taille (cm)")
plt.ylabel("Masse (kg)")
plt.title("Les différents types de joueurs")
plt.show()
|
09° Utiliser ce programme pour obtenir les graphiques correspondants aux zones identifiées par l'algorithme pour k = 5, k=19 et k=27.
Vous devriez obtenir des graphiques semblables à ceux visibles ci-dessous.
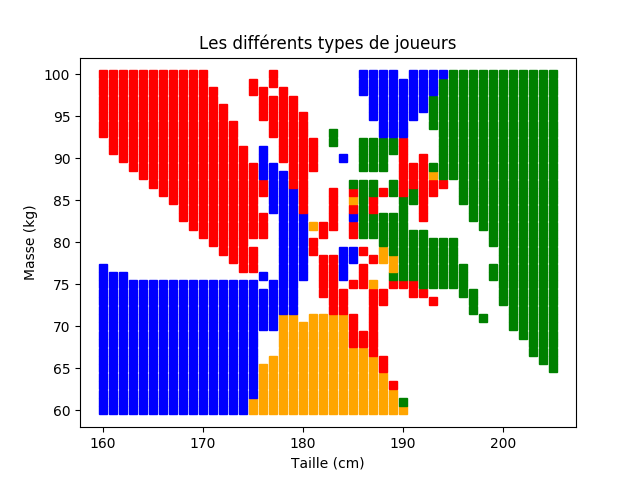
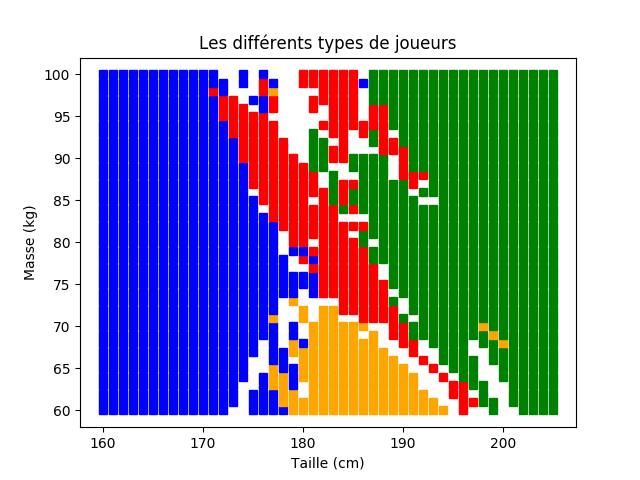
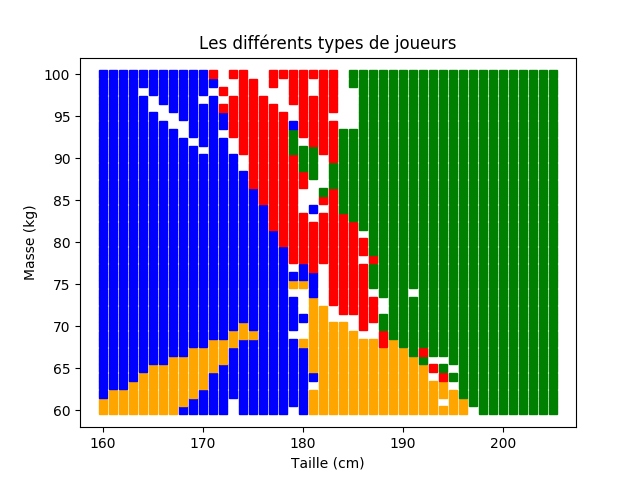
Comme vous le constatez visuellement, chaque valeur de k peut apporter des réponses réellement différentes sur certaines zones des graphiques.
Gardez bien à l'esprit qu'il ne s'agit ici pas d'une réelle catégorisation puisque des joueurs avec un même profil masse-taille peuvent se siter sur des postes différents. Mais cela permet de répondre approximativement à la question initiale.
En se souvenant qu'ici, j'avais pris un exemple où la catégorisation formelle en fonction des simples variables physiques des joueurs est très très simplistes.
Dans la plupart des exemples de knn, on trouve les données d'un dataset comprenant les données sur les Iris. On classifie ces fleurs en trois espèces (les catégories) et on donne les caractéristiques des pétales et des sépales.
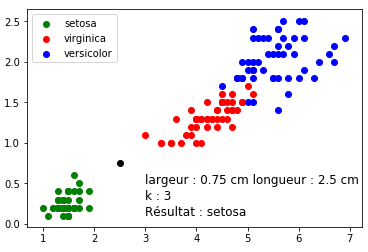
Et ça marche mieux qu'avec les footballeurs car les catégories sont assez peu mélangées.
5 - FAQ
Peut-on créer des graphiques sans créer de liste ?
Oui. Ici, il ne s'agit que de placer des points. Techniquement, il ne s'agit donc pas de courbes et donc nous aurions pu simplement placer des points.
Utiliser les listes me permet simplement de faire des révisions sur leurs créations par compréhension et par extension et ajouts successifs.
Voici une façon alternative (sans liste et donc plus simple) de créer le graphique avec les différents joueurs. Par contre, on notera qu'on ne peut pas juste demander d'afficher les labels : chaque point compte pour un label, il y en aura donc beaucoup. Si vous voulez voir le résultat, vous pouvez enlever le # de la ligne 30.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31 | from creation_collection import creer_collection
from matplotlib import pyplot as plt
# Collection : Création de la collection
joueurs = creer_collection("entrainement.csv")
# Collection : transformation en entiers des descripteurs numériques
for index in range(len(joueurs)):
joueurs[index]['Taille (cm)'] = int(joueurs[index]['Taille (cm)'])
joueurs[index]['Masse (kg)'] = int(joueurs[index]['Masse (kg)'])
# Graphique
for joueur in joueurs:
taille = joueur['Taille (cm)']
masse =joueur['Masse (kg)']
if joueur['Poste'] == 'Attaquant':
plt.plot(taille, masse, 'b+', label="Attaquants")
elif joueur['Poste'] == 'Défenseur':
plt.plot(taille, masse, 'rx', label="Défenseurs")
elif joueur['Poste'] == 'Gardien':
plt.plot(taille, masse, color='orange', marker='+',linewidth=0, label="Milieux de terrain")
elif joueur['Poste'] == 'Milieu de terrain':
plt.plot(taille, masse, 'gx', label="Gardiens de but")
plt.grid()
plt.xlabel("Taille (cm)")
plt.ylabel("Masse (kg)")
plt.title("Les différents types de joueurs")
#plt.legend(loc='upper left')
plt.show()
|
Activité publiée le 23 04 2020
Dernière modification : 02 04 2023
Auteur : ows. h.