2.1 Parcours en largeur d'un graphe
But de l'algorithme du parcours en largeur
Description des attributs nécessaires à l'ALGORITHME
Pour décrire l'algorithme, on utilise souvent les attributs suivants :
- un attribut couleur qui précise l'état du sommet de traitement de ce sommet :
- BLANC : sommet pas encore découvert ;
- GRIS : sommet découvert ;
- NOIR : sommet découvert et totalement traité. On a exploré toutes ses arêtes ou ses arcs sortants. Tous les sommets adjacents sont donc GRIS ou NOIR.
- un attribut distance qui contient le nombre d'arêtes entre ce sommet et le sommet de départ.
INFINI pour les sommets qui n'ont pas encore été découverts. - un attribut parent qui contient le sommet depuis lequel on a découvert ce sommet.
VIDE au départ de l'exploration.
L'algorithme du parcours en largeur d'abord en français
Phase d'initialisation
- Pour chaque sommet u appartenant à l'ensemble S :: on place
- BLANC dans couleur ;
- INFINI dans distance ;
- VIDE dans parent.
- On choisit un sommet de départ qu'on peint en GRIS et qui possède une distance de 0.
- On enfile ce sommet de départ dans une File
Phase de parcours
- TANT QUE la File n'est pas vide
- on défile le prochain sommet qu'on nomme u
- pour chaque sommet v adjacent à u :
- Si v est BLANC
- ↦ On peint v en GRIS
- ↦ On définit la distance de v comme étant la distance de u + 1
- ↦ On définit le parent de v comme étant u
- ↦ On enfile v
- On peint u en NOIR puisqu'on a découvert tous ses sommets adjacents si on arrive ici
- FIN : tous les sommets découvrables ont été traités (NOIR).
Points importants
On agit sur un sommet v que s'il est BLANC. Les actions pointées par la flèche rouge ↦ ne sont donc réalisées qu'une fois sur un sommet donné.
Il est possible que certains sommets ne soient pas découverts à la fin de l'algorithme si le graphe n'est pas connexe. Ils sont alors reconnaissables car leur couleur est BLANC.
2.2 Exemple de parcours en largeur
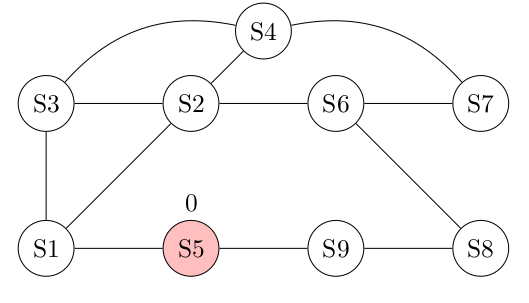
On considère le graphe suivant en prenant le sommet 5 comme point de départ : on cherche donc à déterminer le nombre minimum d'arêtes entre ce sommet et n'importe quel autre sommet du graphe.
Les listes d'adjacence sont considérés être données en suivant les numéros des sommets.
Quelques listes d'adjacence pour que vous comprenniez le principe :
S5 : S1 -> S9
S6 : S2 -> S7 -> S8
Etape initiale
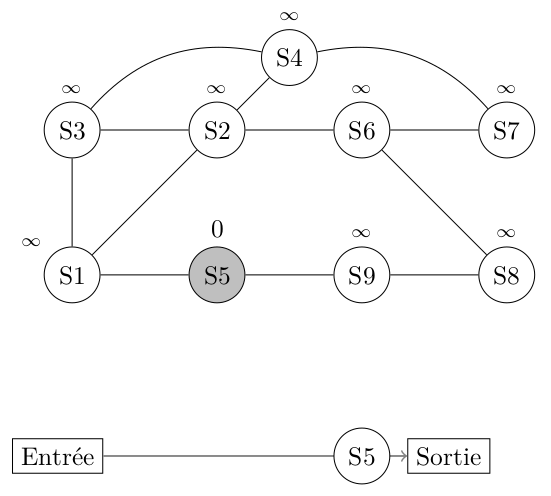
Le sommet 5 est à distance 0 du sommet 5.
Les autres distances sont initialisées à l'infini.
On place le sommet 5 dans la file et on peut commencer.
Défilement de la File -> S5 ->
La File n'est pas vide, on défile et on obtient le sommet S5.
On fait le traitement sur ce sommet 5 puis on lit sa liste d'adjacence : [S1, S9].
- S1 est BLANC, on le peint en GRIS, son parent est S5 et sa distance avec S5 est 0+1, soit 1. On enfile S1.
- S9 est BLANC, on le peint en GRIS, son parent est S5 et sa distance avec S5 est 0+1, soit 1. On enfile S9.
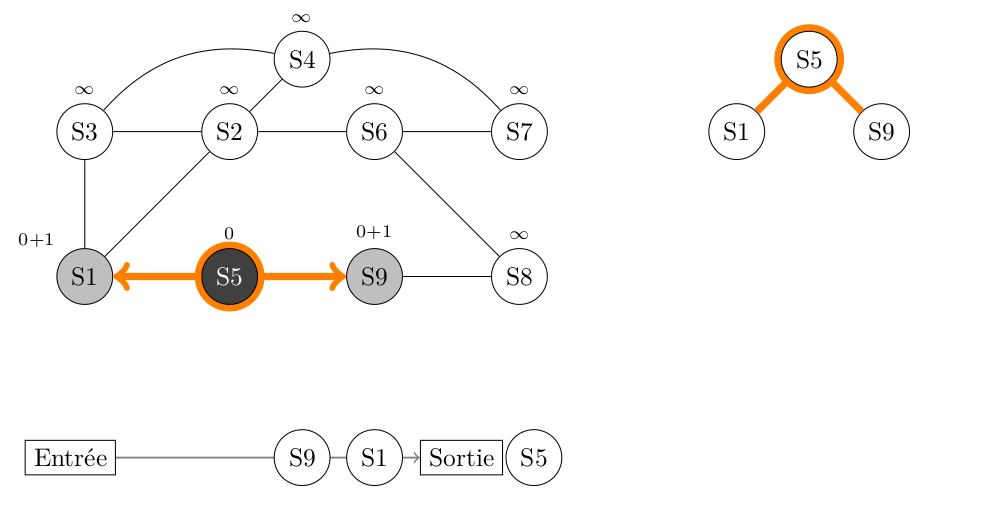
On peint S5 en NOIR pour indiquer que nous avons totalement fini son traitement.
Défilement de la File -> S9 -> S1 ->
La File n'est pas vide, on défile et on obtient le sommet S1.
On fait le traitement sur ce sommet 1 puis on lit sa liste d'adjacence : [S2, S3, S5].
- S2 est BLANC, on le peint en GRIS, son parent est S1 et sa distance avec S5 est 1+1, soit 2. On enfile S2.
- S3 est BLANC, on le peint en GRIS, son parent est S1 et sa distance avec S5 est 1+1, soit 2. On enfile S3.
- S5 n'est pas BLANC, on ne fait rien.
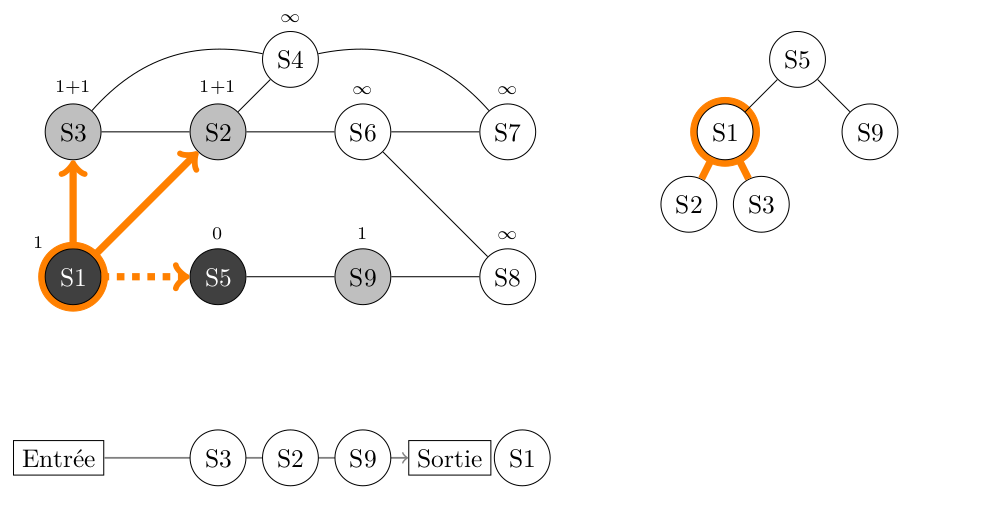
On peint S1 en NOIR pour indiquer que nous avons totalement fini son traitement.
Défilement de la File -> S3 -> S2 -> S9 ->
La File n'est pas vide, on défile et on obtient le sommet S9.
On fait le traitement sur ce sommet 9 puis on lit sa liste d'adjacence : [S5, S8].
- S5 n'est pas BLANC, on ne fait rien.
- S8 est BLANC, on le peint en GRIS, son parent est S9 et sa distance avec S5 est 1+1, soit 2. On enfile S8.
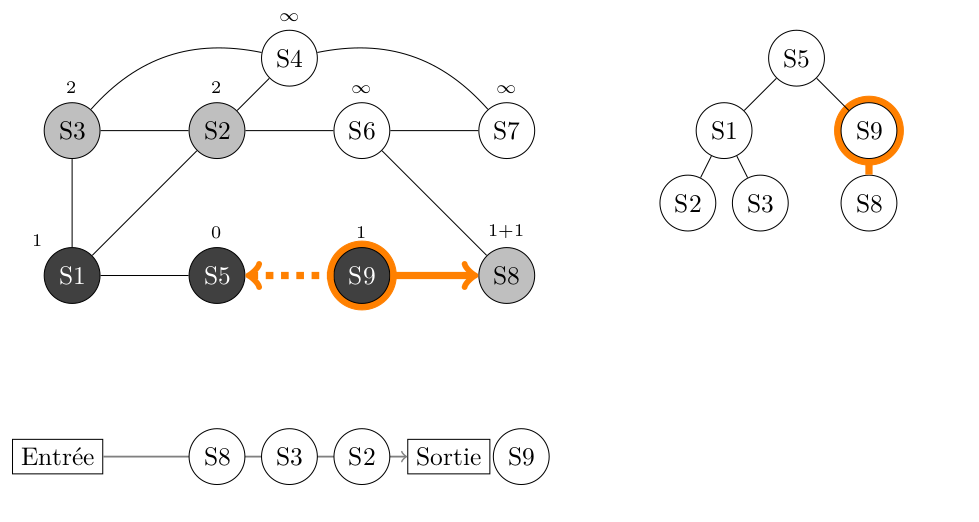
On peint S9 en NOIR pour indiquer que nous avons totalement fini son traitement.
Défilement de la File -> S8 -> S3 -> S2 ->
La File n'est pas vide, on défile et on obtient le sommet S2.
On fait le traitement sur ce sommet 2 puis on lit sa liste d'adjacence : [S1, S3, S4, S6].
- S1 n'est pas BLANC, on ne fait rien.
- S3 n'est pas BLANC, on ne fait rien.
- S4 est BLANC, on le peint en GRIS, son parent est S2 et sa distance avec S5 est 2+1, soit 3. On enfile S4.
- S6 est BLANC, on le peint en GRIS, son parent est S2 et sa distance avec S5 est 2+1, soit 3. On enfile S6.
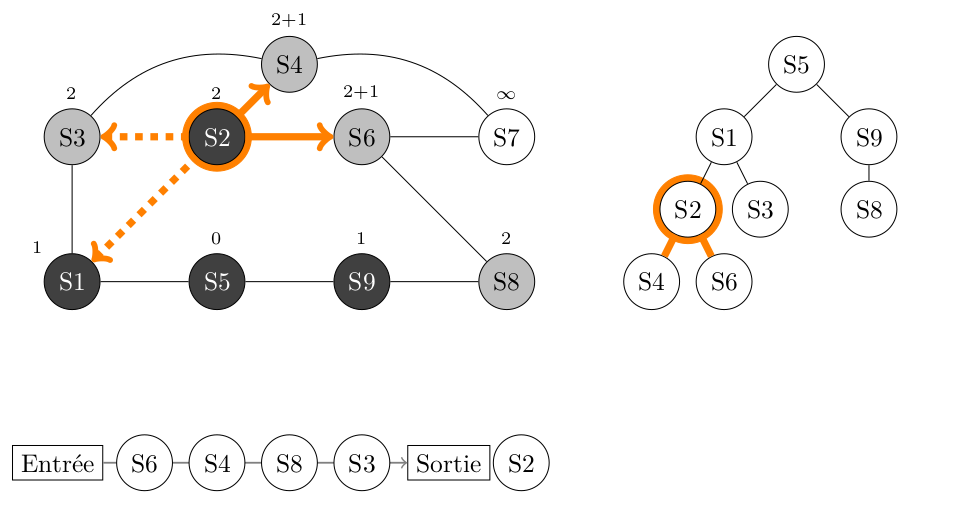
On peint S2 en NOIR pour indiquer que nous avons totalement fini son traitement.
Normalement... vous avez compris le principe.
Défilement de la File -> S6 -> S4 -> S8 -> S3 ->
On traite le sommet S3, on ne fait rien des sommets adjacents à S3 qui sont tous GRIS ou NOIR, puis on place S3 en NOIR.
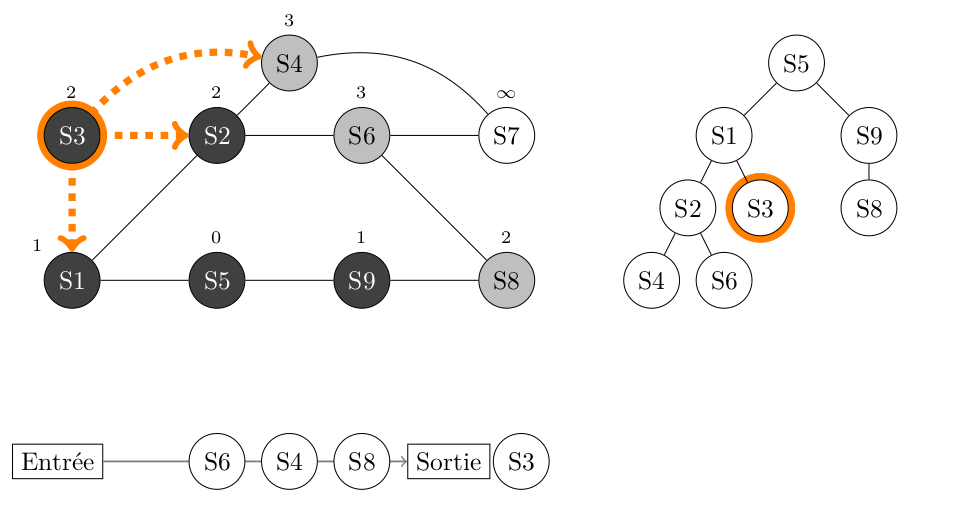
Défilement de la File -> S6 -> S4 -> S8 ->
On traite le sommet S8, on ne fait rien des sommets adjacents à S8 qui sont tous GRIS ou NOIR, puis on place S8 en NOIR.
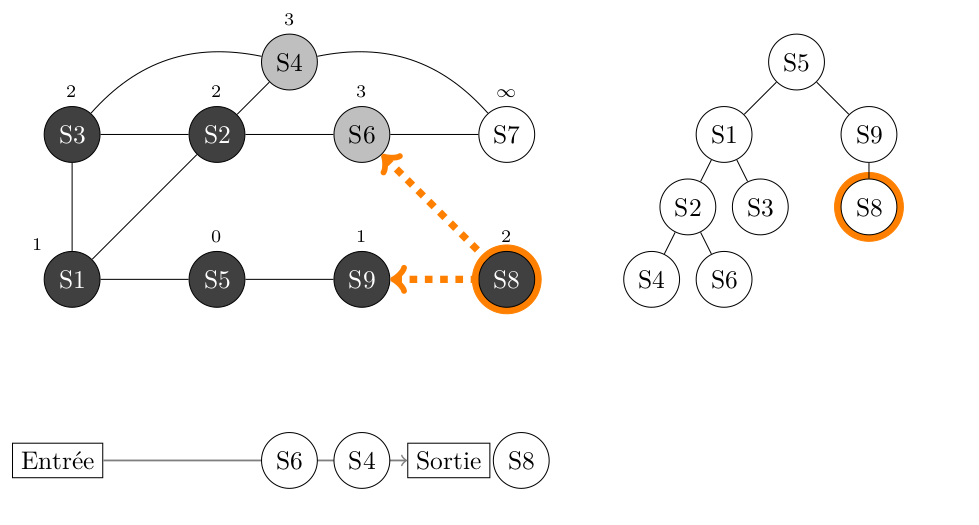
Défilement de la File -> S6 -> S4 ->
La File n'est pas vide, on défile et on obtient le sommet S4.
On fait le traitement sur ce sommet 2 puis on lit sa liste d'adjacence : [S2, S3, S7].
- S2 n'est pas BLANC, on ne fait rien.
- S3 n'est pas BLANC, on ne fait rien.
- S7 est BLANC, on le peint en GRIS, son parent est S4 et sa distance avec S5 est 3+1, soit 4. On enfile S7.
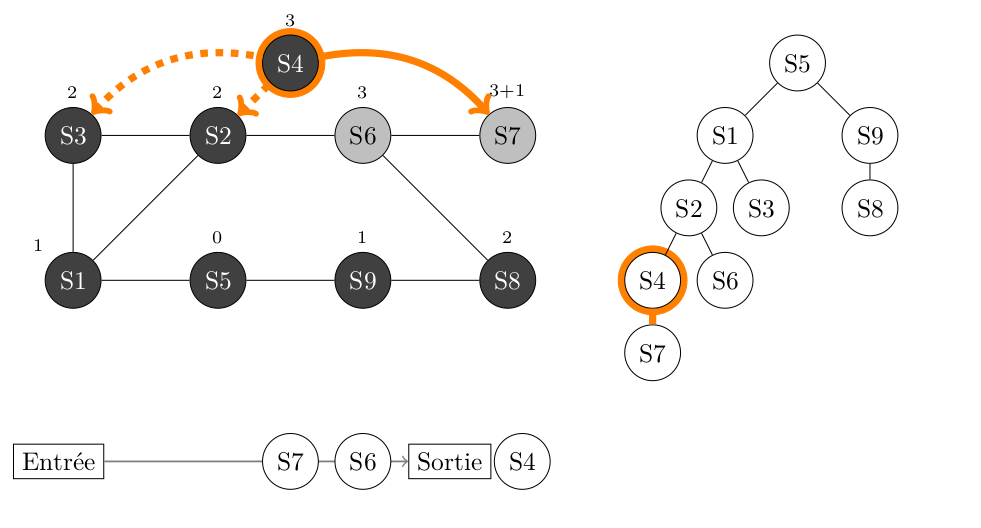
Défilement de la File -> S7 -> S6 ->
On traite le sommet S6, on ne fait rien des sommets adjacents à S6 qui sont tous GRIS ou NOIR, puis on place S6 en NOIR.
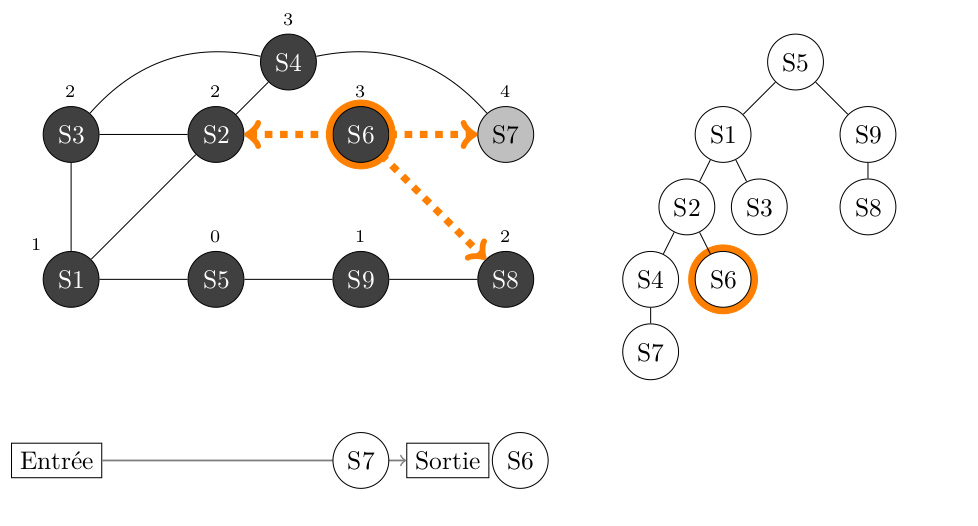
Défilement de la File -> S7 ->
On traite le sommet S7, on ne fait rien des sommets adjacents à S7 qui sont tous GRIS ou NOIR, puis on place S7 en NOIR.
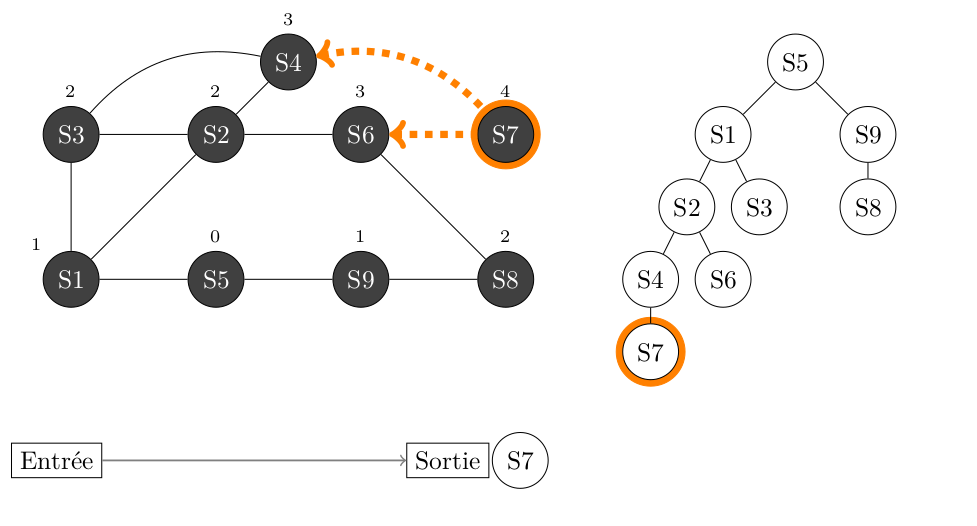
File VIDE : on stoppe la boucle
Après exécution de l'algorithme, on obtient :
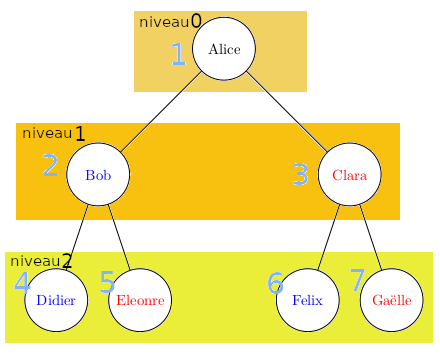
- Un Arbre dont la racine est le sommet de départ et qui mène à tous les autres sommets : cela permet de connaître UN chemin entre le sommet de départ et les autres.
- La distance minimale en nombre d'arêtes entre le sommet de départ et n'importe quel autre sommet : c'est la profondeur du sommet (on prend la convention profondeur 0 pour la racine).
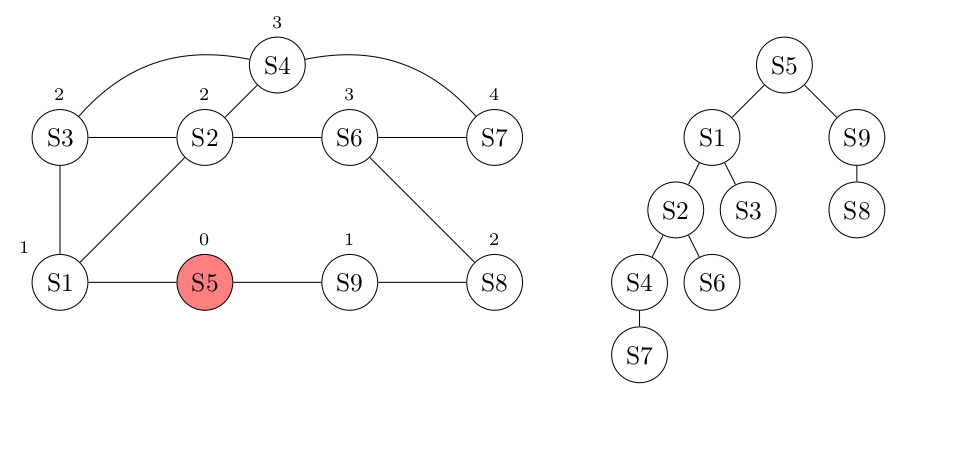
Et voici le graphe correspondant à l'arbre du parcours, obtenu en supprimant les arêtes que nous n'avons pas utilisés lors de la création de l'arbre :
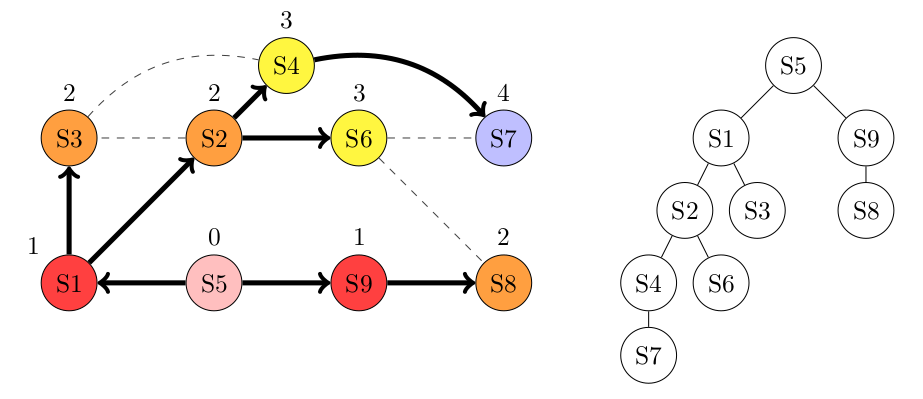
3.3 Questions de compréhension
✎ 01° Sur l'Arbre de parcours obtenu, quel est l'enchaînement de sommets obtenu pour aller du sommet S5 au sommet S6 ?
✎ 02° Compter le nombre d'arêtes utilisées pour aller de S5 à S6. Obtient-on bien une distance de 3 comme indiqué au dessus du sommet 6 sur le graphe ?
✎ 03° Pourquoi la distance indiquée pour S5 sur le graphe est-elle de 0 ?
04° On utilise une fois chaque sommet comme centre de recherches. Combien de fois utilise-t-on les arêtes ?
- On utilise une fois chaque arête
- On utilise deux fois chaque arête
- On utilise trois fois chaque arête
- J'aime ni les arêtes, ni le poisson
...CORRECTION...
On utilise les arêtes dans les deux sens. Donc deux fois.
05° On cherche la complexité de cet algorithme en prenant comme référence le nombre de fois où on teste si un sommet est BLANC. On considère uniquement un graphe connexe. Notons a le nombre d'arêtes. La complexité de cet algorithme est :
- Logarithmique en fonction de a ?
- Linéaire en fonction de a ?
- Quadratique en fonction de a ?
- Exponentielle en fonction de a ?
...CORRECTION...
Puisqu'on utilise deux fois les arêtes, on peut noter 𝞗(2a). Comme on ne s'intéresse pas au facteur multiplicatif, on obtient donc 𝞗(a). La bonne réponse est donc linéaire.
Le coût total d'exécution dépend en réalité du nombre de sommets et du nombre d'arêtes. Par contre, si le graphe n'est pas connexe, on peut très bien ne pas rencontrer ni traiter certains sommets et certains arcs ou arêtes.
On peut donc écrire 𝞞(s+a)
06° En prenant le graphe, donner deux chemins de distance 3 allant de S5 à S6.

Quel est le parent unique de S6 sur l'Arbre de parcours obtenu ? En déduire le chemin qui va être choisi ici si on suit l'Arbre de parcours.
...CORRECTION...
S5-S1-S2-S6 ou S5-S9-S8-S6.
On voit sur l'Arbre qu'on obtiendrait ici le premier choix car le parent de S6 est S2.
Le parent de S2 est S1.
Le parent de S1 est S5.
07° Peut-on trouver un chemin de moins de 3 arêtes menant de S5 à S6 ?
...CORRECTION...
Non : le parcours en largeur donne 3. Il n'y a donc pas de chemin plus court que 3 arêtes.
3 - Algorithme de parcours en largeur
Nous avons vu l'algorithme décrit en français, voyons son pseudo-code.
3 Pseudo-code du parcours en largeur d'un graphe
BUT
découvrir un chemin de plus petite distance entre le sommet de départ et chaque sommet accessible.
ENTREES
- Un graphe noté g
- Un sommet s qui servira de sommet origine
SORTIE
Aucune ici mais on peut facilement modifier l'algorithme pour qu'il renvoie par exemple l'arbre de parcours.
ALGORITHME PARCOURS EN LARGEUR
Phase 1 d'initialisation
POUR chaque sommet u appartenant au graphe g
u.couleur ← BLANC
u.distance ← INFINI
u.parent ← VIDE
Fin Pour
s.couleur ← GRIS
s.distance ← 0
s.parent ← VIDE
a_traiter ← nouvelleFileVide()
enfiler(a_traiter, s)
Phase 2 de parcours
TANT QUE NON estFileVide(a_traiter)
u ← defiler(a_traiter)
POUR chaque sommet v appartenant à la liste d'adjacence du sommet u
SI v.couleur est BLANC
si on arrive ici, c'est que le sommet n'a pas encore été découvert
v.couleur ← GRIS
v.distance ← u.distance + 1
v.parent ← u
enfiler(a_traiter, v)
Fin Si
u.couleur ← NOIR
Fin Pour
Fin Tant Que
Renvoyer VIDE (∅)
4 - Exercices
Maintenant que vous avez vu l'exécution une première fois et que vous avez vu l'algorithme, il est temps de vous l'approprier.
Nous l'utiliserons dans le cadre d'un mini-projet on nous tenterons de faire sortir un personnage d'un labyrinthe, alors que des monstres rodent...
✎ 08° Fournir les listes d'adjacence des sommets ci-dessous. On placera toujours les sommets dans l'ordre alphabétique.
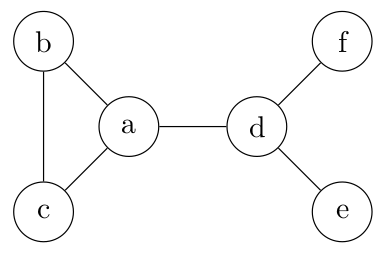
✎ 09° Fournir l'arbre de parcours obtenu à partir du sommet c.
✎ 10° Fournir les listes des successeurs des sommets ci-dessous. Attention, cette fois le graphe est orienté. On placera toujours les sommets dans l'ordre alphabétique.
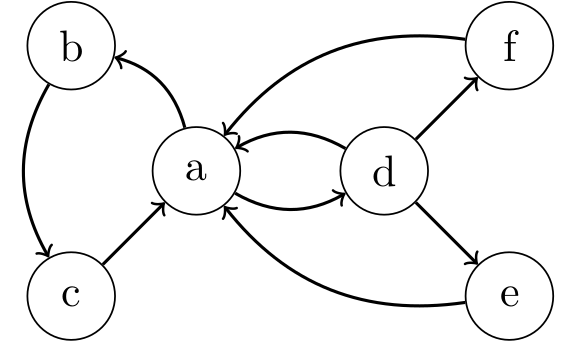
✎ 11° Fournir l'arbre de parcours obtenu à partir du sommet c. Il faudra bien entendu ne prendre que la liste des successeurs.
✎ 12° Fournir l'arbre de parcours obtenu à partir du sommet a.
✎ 13° Fournir l'arbre de parcours obtenu à partir du sommet d.
✎ 14° Quel semble être le sommet le plus central ?
✎ 15° Le parcours en largeur fonctionne pour trouver le plus court chemin dans un graphe orienté non pondéré. Expliquez pourquoi il ne fonctionne pas pour un graphe pondéré.
5 - FAQ
Et on fait comment sur un graphe pondéré ?
On applique l'algorithme de Dijkstra.
Et avec un traitement naïf en Python, ça donne quoi ?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118 | |
Voici le résultat du programme de test précédent :
Graphe en tant que dictionnaire :
{0: [1, 2], 1: [0, 3], 2: [0, 3], 3: [1, 2, 4], 4: [3]}
Résultat du parcours en largeur d'abord
(0, {'couleur': 2, 'distance': 0, 'parent': None})
(1, {'couleur': 2, 'distance': 1, 'parent': 0})
(2, {'couleur': 2, 'distance': 1, 'parent': 0})
(3, {'couleur': 2, 'distance': 2, 'parent': 1})
(4, {'couleur': 2, 'distance': 3, 'parent': 3})
Recherche du chemin entre 0 et 3
[0, 1, 3]
Et avec un bon traitement en Python, ça donne quoi ?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88 | |
Activité publiée le 29 04 2021
Dernière modification : 29 04 2021
Auteur : ows. h.