9 - Preuve du tri par sélection

⏪

⏬

⏩

1 - Rappel

2 - Terminaison

3 - Coût

4 - Correction

5 - Python

6 - FAQ

Une activité-leçon assez théorique et mathématique par certains côtés.

Quasiment toutes les questions sont munies de la correction.

Logiciel nécessaire pour l'activité : Python 3 : Thonny, IDLE ou le site repl.it ...

Prérequis : Algorithme : tri par sélection

Evaluation ✎ : questions -

Documents de cours : open document ou pdf

Résumé de cours : open document ou pdf

MODE COURS (cacher les questions)

1 - Rappel visuel du tri et algorithme

⇩ ⇧ ⤊

Nous avons tout vu dans l'activité précédente. Si vous ne vous en souvenez plus trop, voici l'animation suivi de l'algorithme.

Tri par sélection du plus petit au plus grand


Index	00	01	02	03	04	05	06	07	08	09	10	11	12	13	14	15	16	17	18	19
Elément	60	89	15	56	82	1	86	97	24	86	75	6	14	69	98	31	37	89	91	56

Algorithme de tri par sélection

But : trier sur place un tableau initialement non trié.

(ici par odre croissant)

Description des entrées / sortie

ENTREES :

tableau : un tableau contenant au moins deux éléments.
(optionnelle selon les langages d'implémentation): longueur, le nombre d'éléments dans le tableau

SORTIE : aucune. Le tableau est trié sur place. On modifie directement tableau.

Exemple :

Prenons tableau = [13, 18, 89, 1024, 45, -12, 18]

Initialement le tableau contient donc cela :

Indice	0	1	2	3	4	5	6
Elément	13	18	89	1024	45	-12	18

Après le tri, le tableau contiendra cela :

Indice	0	1	2	3	4	5	6
Elément	-12	13	18	18	45	89	1024

En Français

Pour chaque indice debut possible dans le tableau

On cherche l'indice indice_min contenant le plus petit élément dans le sous-tableau [debut ; longueur - 1].
On intervertit les contenus des cases des indices debut et indice_min.

Algorithme

debut est l'indice (flèche en vert clair dans l'animation) de la case à remplir

POUR debut variant de 0 à (longueur - 1)

indice_min ← minimum(tableau, debut)

on cherche l'indice de la plus petite valeur présente dans la partie non triée [debut ; longueur - 1]

intervertir(tableau, debut, indice_min)

on intervertit les valeurs situées aux indices debut et indice_min

Fin POUR

Renvoyer VIDE (∅)

Algorithme de minimum(tableau, debut)

Algorithme

debut est l'indice (flèche en vert clair dans l'animation) de la case à remplir

indice_min ← debut

POUR i variant de (debut + 1) à (longueur - 1)

SI tableau[i] < tableau[indice_min]

indice_min ← i

Fin SI

Fin POUR

Renvoyer indice_min

Algorithme de intervertir(tableau, i, j)

Algorithme

temp ← tableau[i]

tableau[i] ← tableau[j]

tableau[j] ← temp

Renvoyer Vide

2 - Preuve de terminaison

⇩ ⇧ ⤊

Rappel : Preuve de terminaison

La preuve de terminaison d'un algorithme permet d'affirmer qu'il s'arrête de façon certaine sur toutes les entrées valides qu'on lui fournit (c'est à dire les entrées respectant les préconditions).

Preuve de terminaison : si les deux propositions suivantes sont vraies alors la boucle s'arrête :

Proposition A : les boucles s'expriment sous la forme TANT QUE VARIANT > 0
Proposition B : le VARIANT est une suite d'ENTIERS strictement décroissante.

(A et B) implique alors que l'algorithme se termine.

Attention à la négation

(A et B) implique que l'algorithme s'arrête TOUJOURS.

NON (A et B) ou encore (NON A) ou (NON B) d'après De Morgan n'implique rien de particulier.
Il est possible que l'algorithme ne boucle jamais, boucle parfois ou boucle toujours.

Voici l'algorithme minimum.

debut est l'index (flèche en vert clair dans l'animation) de la case à remplir

indice_min ← debut

POUR index variant de (debut + 1) à (longueur - 1)

SI tableau[index] < tableau[indice_min]

indice_min ← index

Fin SI

Fin POUR

Renvoyer indice_min

01° Montrer la terminaison de cet algorithme minimum.

Correction ?

...CORRECTION...

Nous avons un compteur partant de (debut + 1) et augmentant jusqu'à atteindre (longueur - 1).

Notons k le numéro du tour de boucle.

La boucle bornée POUR peut donc s'écrire :

TANT QUE debut + 1 + k < longueur

TANT QUE 0 < longueur - debut - 1 - k

Il suffit d'écrire l'inégalité dans l'autre sens :

TANT QUE longueur - debut - 1 - k > 0

Si on pose u₀ = longueur - debut - 1, on peut alors écrire le VARIANT sous la forme u_k = u_O - k

Il s'agit d'une suite d'entiers strictement décroissante.

On obtient finalement :

TANT QUE u_k > 0

avec le VARIANT u_k est une suite strictement décroissante d'entiers.

On en conclut que l'algorithme se termine.

Regardons maintenant notre algorithme de tri.

debut est l'index (flèche en vert clair dans l'animation) de la case à remplir

POUR debut variant de 0 à (longueur - 1)

indice_min ← minimum(tableau, debut)

on cherche l'index de la plus petite valeur présente dans la partie non triée (index debut et plus)

intervertir(tableau, debut, indice_min)

on intervertit les valeurs situées aux index debut et indice_min

Fin POUR

Renvoyer VIDE (∅)

02° Montrer la terminaison de cet algorithme de tri.

Correction ?

...CORRECTION...

Nous avons un compteur partant de 0 et augmentant jusqu'à atteindre (longueur - 1).

Notons k le numéro du tour de boucle.

La boucle peut alors s'écrire :

TANT QUE 0 + k < longueur

TANT QUE 0 < longueur - k

TANT QUE longueur - k > 0

On en conclut encore une fois que cette boucle POUR se termine puisque le terme de gauche correspond bien à une suite strictement décroissante d'entiers : il devient de plus en plus petit à chaque tour de boucle.

L'algorithme se termine donc car :

La fonction minimum se termine
La fonction intervertir se termine (il s'agit juste de 3 affectations)
La boucle POUR principale qui contient les deux fonctions précédentes se termine également

Comme il s'agit de boucles FOR, il suffit de façon moins rigoureuse de simplement vérifier qu'on ne modifie pas la variable de boucle en cours de boucle, que la longueur du tableau n'augmente pas par exemple ou que les actions internes à la boucle se termine.

3 - Coût du tri par sélection

⇩ ⇧ ⤊

Nous allons prendre comme critère de coût le nombre de comparaisons à effectuer lorsque notre tableau possède n éléments. La variable longueur contient donc la valeur n.

Algortihme du tri par sélection

debut est l'index (flèche en vert clair dans l'animation) de la case à remplir

POUR debut variant de 0 à (longueur - 1)

indice_min ← minimum(tableau, debut)

on cherche l'indice de la plus petite valeur présente dans la partie non triée [debut; longueur -1]

intervertir(tableau, debut, indice_min)

on intervertit les valeurs situées aux indices debut et indice_min

Fin POUR

Renvoyer VIDE (∅)

Et voici l'algorithme de la fonction minimum.

Algorithme de `minimum(tableau, debut)`

debut est l'indice (flèche en vert clair dans l'animation) de la case à remplir

indice_min ← debut

POUR i variant de (debut + 1) à (longueur - 1)

SI tableau[i] < tableau[indice_min]

indice_min ← i

Fin SI

Fin POUR

Renvoyer indice_min

04° On considère un tableau de n éléments. On considère qu'on effectue le premier tour de boucle. La variable debut contient donc 0. Combien de comparaisons va devoir faire l'algorithme minimum avant de renvoyer sa réponse ?

Attention, dans les versions "Algorithme" des boucles POUR, on donne bien la vraie valeur finale. Pas la borne extrême supérieure qu'on n'atteint pas. Ce n'est pas comme avec le range de Python.

Correction ?

...CORRECTION...

La variable debut contient 0. La variable index commence donc à 1.

La longueur vaut n. La variable i finit donc à n-1.

La lecture de l'algorithme de la fonction nous montre donc que la variable i va prendre les valeurs successives 1 ... jusqu'à n-1. Au total, on a donc n-1 comparaisons.

05° On considère le deuxième tour de boucle. La variable debut contient donc 1. Combien de comparaison va devoir faire la fonction minimum avant de renvoyer sa réponse sur ce tour de boucle ? Combien a-t-il fallu de comparaisons au total pour l'instant ?

Correction ?

...CORRECTION...

La variable debut contient 1. La variable index commence donc à 2.

La longueur vaudra toujours n. La variable index finit donc à n-1.

La lecture de l'algorithme de la fonction nous montre donc que la variable index va prendre les valeurs successives 2 ... jusqu'à n-1. Au total, on a donc n-2 comparaisons.

Au total, on a donc n-1 + n-2 comparaisons.

06° A votre avis, combien de comparaisons au total lors du prochain tour de boucle ?

Correction ?

...CORRECTION...

On va rajouter n-3 comparaisons.

Au total, on a donc n-1 + n-2 + n-3 comparaisons.

07° Combien l'algorithme va-t-il faire de comparaisons pour déterminer le contenu de l'avant-dernière cas, lorsque debut vaut longueur-2 ?

Correction ?

...CORRECTION...

La variable debut contient longueur-2, soit n-2. La variable index commence donc à n-1.

La longueur vaudra toujours n. La variable index finit donc à n-1.

On aura donc une simple comparaison effectuée.

08° Combien l'algorithme va-t-il faire de comparaisons pour déterminer le contenu du dernière cas, lorsque debut vaut longueur-1 ?

Combien de comparaisons aura-t-on effectué au total sur tout le tableau ?

Correction ?

...CORRECTION...

La variable debut contient longueur-1, soit n-1. La variable index commence donc à n.

La longueur vaudra toujours n. La variable index finit donc à n-1.

La boucle ne va donc pas fonctionner (croissant, mais le début est supérieur à la fin) et il n'y aura pas de comparaisons.

Au total, on a donc ce nombre de comparaisons :

C_n = 1 + 2 + 3 + 4 + 5 + ... + (n-5) + (n-4) + (n-3) + (n-2) + (n-1)

Cela devrait vous rappeler des souvenirs. Nous avons déjà rencontré cette série et nous avions démontré sa formule.

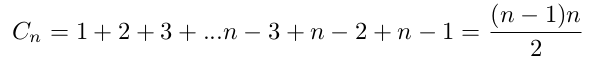
Comme cette somme est longue à écrire, on utilise parfois la notation ci-dessous qui veut dire exactement la même chose :

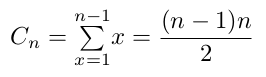
09° Démontrer cette formule (sans utiliser les formules vues éventuellement en spécialité mathématiques de première).

Correction ?

...CORRECTION...

Notre série C_n est la somme de (n-1) éléments :

C_n = 1 + 2 + 3 + 4 + ... + (n - 4) + (n - 3) + (n - 2) + (n - 1)

Nous voudrions associer les éléments deux par deux, mais il est possible qu'ils soient en nombre impair. Comment faire ? Multiplier chacun des membres par deux !

2 * C_n = 1 + 1 + 2 + 2 + 3 + 3 + 4 + 4 + ... + (n - 4) + (n - 4) + (n - 3) + (n - 3) + (n - 2) + (n - 2) + (n - 1) + (n - 1)

Du coup, le membre de droite comporte maintenant le double d'éléments, soit 2(n-1) éléments. Nous sommes certain qu'il y a un nombre pair d'éléments.

Associons alors les 2(n-1) éléments deux par deux, par complément du type 3 + (n - 3).

Cela nous permettra d'obtenir (n-1) couples.

2 * C_n = 1 + (n - 1) + 1 + (n - 1) + 2 + (n - 2) + 2 + (n - 2) + 3 + (n - 3) + 3 + (n - 3) + 4 + (n - 4) + 4 + (n - 4) + ...

2 * C_n = (1 + n - 1) + (1 + n - 1) + (2 + n - 2) + (2 + n - 2) + (3 + n - 3) + (3 + n - 3) + (4 + n - 4) + (4 + n - 4) + ...

Nous voyons donc que nous obtenons (n-1) couples qui valent tous n.

2 * C_n = (n) + (n) + (n) + (n) + (n) + (n) + (n) + (n) + ...

On peut donc écrire

2*C_n = (n-1)n

Au final, cela donne donc :

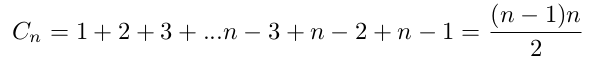
10° Retrouver la formule en utilisant cette fois les formules habituelles sur quelques séries typiques.

Série arithmétique des nombres de 1 à n

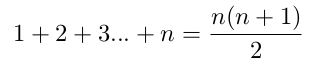
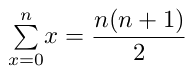formule 1'

Série arithmétique des carrés de 1² à n²

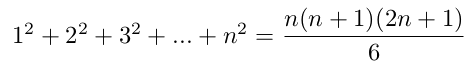
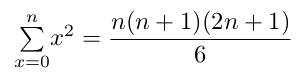formule 2

Série arithmétique des cubes de 1³ à n³

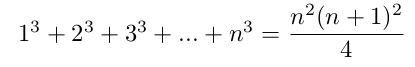
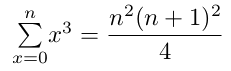formule 3

Série géométrique (un exemple avec x différent de 0)

Formule de la série géométrique de l'exemple

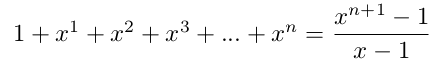
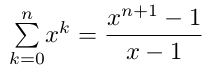formule 4

Correction ?

...CORRECTION...

Il suffit de prendre la formule (1) qui correspond à une somme de 1 à n.

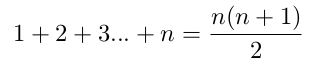
On pose donc n = n' - 1.

On remplace donc

n par n'-1
n+1 par n'-1+1, soit n'

On obtient donc bien la formule suivante en renommant simplement notre variable n.

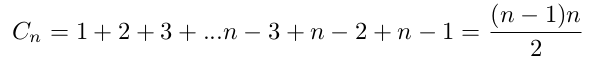
11° QCM : que peut-on écrire de la complexité du tri par sélection ?

A : Elle est logarithmique (𝞗(lg n) ), c'est à dire que la complexité évolue moins vite que le nombre n de données. Exemple : si on multiplie les données par 8, on ne rajoute que 3 opérations.
B : Elle est linéaire ( 𝞗(n) ), c'est à dire que la complexité évolue comme le nombre n de données (par exemple : si on multiplie le nombres de données n par 8, le temps d'exécution est multiplié par 8)
C : Elle est quadratique ( 𝞗(n²) ), c'est à dire que la complexité évolue comme le carré du nombre n de données (par exemple : si on multiplie le nombres de données n par 8, le temps d'exécution est multiplié par 64, 10*10)
D : Elle est exponentielle ( 𝞗(xⁿ) ), c'est à dire que la complexité évolue à terme beaucoup plus vite que n'importe quelle fonction polynomiale du nombre n de données (par exemple : si on passe de 10 à 80 données (x8), le temps d'exécution est multiplié par 10²¹ !)

Correction ?

...CORRECTION...

On cherche à voir uniquement le comportement global de cet algorithme lorsqu'on augmente les données qu'il doit traiter.

On va donc simplifier notre formule : le but est de savoir à quelle type de fonction se rapproche le coût de notre algorithme, pas la formule exacte de cette fonction (nous l'avons déjà !).

On omet donc d'abord les facteurs multiplicateurs ou diviseurs. Ici, le facteur 2.

Pourquoi ? Voyons un exemple : un algorithme a un coût en n²*5.

Cas 1 : on tient compte du facteur 5 pour nos comparaisons sur le même algorithme.

Pour n = 2 données, on obtient un coût de 2*2*5 = 20.

Pour n = 4 données, on obtient un coût de 4*4*5 = 80.

On voit donc que lorsqu'on double les données (on passe de 2 à 4), le coût est lui multiplié par 4 (on passe de 20 à 80).

Cas 2 : on ne tient pas compte du facteur 5 pour nos comparaisons sur le même algorithme.

Pour n = 2 données, on obtient un coût de 2*2 = 4.

Pour n = 4 données, on obtient un coût de 4*4 = 16.

On voit donc que lorsqu'on double les données (on passe de 2 à 4), le coût est lui multiplié par 4 (on passe de 4 à 16).

Conclusion : inutile de tenir compte des facteurs multiplicateurs lorsqu'il s'agit de trouver le comportement d'un même algorithme lorsqu'on change la taille de ses données.

Il nous reste donc (n-1)*n.

Pour les grands nombres, on peut omettre le -1 du n-1. En terme d'évolution globale, il n'y a pas vraiment de différence entre 1 milliard et 1 milliard moins 1...

On voit donc qu'on obtient n*n, soit n².

Le coût est donc quadratique.

Complexité du tri par sélection

On retiendra donc que la complexité du tri par sélection est 𝞗(n²) : le coût est quadratique dans tous les cas.

Si on s'en tient aux comparaisons comme critère de sélection, on peut donc dire que le tri par insertion est meilleur : le coût du tri par insertion est quadratique dans le pire des cas mais linéaire dans le meilleur des cas.

Attention, néanmoins : on pourrait choisir d'autres critères. Comme les déplacements d'éléments. Et dans ce cas, le tri par sélection pourrait être vu comme meilleur que le tri par insertion !

4 - Preuve de correction

⇩ ⇧ ⤊

Nous avons donc démontré

la terminaison du tri par sélection : nous sommes maintenant certain qu'il va s'arrêter pourvu qu'on lui en laisse le temps
le coût quadratique dans tous les cas : nous savons que si on multiplie la taille des données par 10, le temps d'exécution va approximativement être multiplié par 100. Ceci en considérant la comparaison comme étant le critère de rapidité.

Oui mais... Est-ce que notre algorithme marche à chaque fois. Après tout, nous avons fait quelques essais, rajouté quelques doctests. Mais il y a peut-être des cas (même rares) qui risquent de créer un raté. Non ?

Imaginez : vous avez la responsabilité d'un grand nombre de vie en travaillant sur un algorithme de pilotage automatique. L'un des processus que vous avez créé utilise un tri par sélection. S'il disfonctionne, c'est la perte de contrôle de l'appareil. Vous avez fait des tests. Vous savez que ça marche. Mais... Laisseriez-vous l'appareil décoller sans être certain que ça fonctionne toujours ?

Tests

A toujours avoir en tête : on ne peut pas prouver la correction d'un algorithme (et de la fonction programmée correspondante) en réalisant juste un très grand nombre de tests : nous ne parviendrions qu'à prouver que l'algortihme fonctionne dans tous les cas testés.

Cela n'est pas équivalent à affirmer qu'il est réellement correct dans tous les cas.

Attention, tous les cas veut dire : tous les cas dont les entrées vérifient bien les spécifications d'entrée.

Voyons maintenant la preuve de correction de cet algorithme.

Preuve de correction et invariant

Définitions

La preuve de correction d'un algorithme permet d'affirmer

qu'il fournit toujours une réponse correcte
sur toutes les entrées valides qu'on lui fournit.

Pour faire la preuve de correction d'un algorithme, il faut trouver un INVARIANT : une propriété P vérifiable qui reste vraie lors des différentes étapes de l'algorithme.

Un INVARIANT DE BOUCLE est une propriété VRAIE à chaque début de tour, juste avant l'exécution de la première instruction de la boucle.

Cet invariant permettra de prouver que le résultat final après exécution est bien le résultat attendu.

Malheureusement, il n'y a pas de méthodologie automatique miraculeuse pour trouver cet invariant. Il faut réfléchir et tenter des choses, comme avec toute démonstration.

Démonstration en 3 phases : Initialisation-Conservation-Terminaison

Une fois qu'on dispose d'un INVARIANT P, la démonstration se fait en trois temps.

Phase d'initialisation : P₀ est VRAI

On doit prouver que l'INVARIANT est VRAI lorsqu'on commence le premier tour de boucle mais sans l'avoir réalisé en entier. On a donc fait 0 tour en entier.

Le plus souvent, cette partie est triviale. Mais pas toujours...

Phase de conservation : P_k ➡ P_k+1

SI P est vrai après k tours de boucles, ALORS P sera encore vrai en ayant fait un tour de boucles supplémentaire.

Hypothèse de départ :

On fait l'hypothèse qu'on a fait k tours de boucles et qu'on est au début du tour k+1. L'INVARIANT P_k est donc considéré juste.

Déroulement du tour de boucle (k+1) jusqu'au début du prochain

On doit montrer qu'en réalisant ce tour complétement jusqu'au début du prochain, l'invariant P reste vrai à la fin de cette boucle. On aura donc fait k+1 tours de boucle complet, P_k+1 serait encore vérifiée.

On se place dans le cadre d'un tour qui est suivi d'un autre tour. On ne se place pas dans le cadre de la toute dernière boucle ici. On boucle, point.

On peut donc écrire P_k ➡ P_k+1

Phase de terminaison

On doit y prouver qu'à la fin du dernier tour, on obtient la situation voulue. Ni trop tôt, ni trop tard. C'est pour cela qu'on nomme cette partie la phase de terminaison, à ne pas confondre avec la preuve de terminaison.

P₀ ➡ P₁ ➡ P₂ ➡ P₃... ➡ P_final

Le problème est qu'il n'existe pas de méthode automatique pour trouver le bon invariant. Il faut chercher à chaque nouveau problème qui se pose...

Autre difficulté : le numéro de l'étape ne correspond pas nécessairement à la valeur de la variable de boucle si elle commence à 0 : à la fin du premier tour de boucle, k vaut 1 mais la variable de boucle 0. A la fin du deuxième tour de boucle, k vaut 2 mais la variable de boucle 1...

Le cas du tri par sélection peut se résumer à ceci : on décompose le problème en

un sous-tableau trié (à gauche) et
un sous-tableau non-trié (le reste, à droite).

On remplit le sous-tableau trié en ramenant les minimums successifs qu'on trouve dans le sous-tableau non trié.

Invariant du tri par sélection

Au départ, le sous-tableau des éléments triés est vide. On rajoute 1 élément dans ce tableau à chaque tour de boucle.

On considère que notre invariant pourrait être la propriété P_k suivante : après k tours de boucle, k éléments sont triés dans le sous-tableau [0;k-1] de gauche.

Dans le sous-tableau trié (par ordre croissant ici), on doit donc avoir tableau[x] < tableau[x+1].

12° Travaillons sur l'initialisation.

Questions

Si on n'est pas encore rentré dans la boucle, combien a-t-on d'éléments dans notre sous-tableau trié ?
Peut-on considérer que l'invariant est vérifié pour P₀ ?

Correction ?

...CORRECTION...

P₀ signifie qu'on a 0 éléments triés.

Le sous-tableau trié est donc vide. Il ne contient rien. Cela revient à avoir [].

On peut sans peine se convaincre qu'un sous-tableau ne contenant aucun élément est bien trié.

On peut donc dire que l'invariant est vrai avant l'exécution de la première boucle FOR. P₀ est vérifié.

Passons maintenant à la conservation. Pour rappel, voici l'algorithme :

Algorithme de tri par sélection

debut est l'index (flèche en vert clair dans l'animation) de la case à remplir

POUR debut variant de 0 à (longueur - 1)

indice_min ← minimum(tableau, debut)

on cherche l'indice de la plus petite valeur présente dans la partie non triée [debut; longueur -1]

intervertir(tableau, debut, indice_min)

on intervertit les valeurs situées aux indices debut et indice_min

Fin POUR

Renvoyer VIDE (∅)

13° Quelle va être la première valeur prise par debut ? Que va contenir tableau[debut] après la première boucle ? Combien va-t-on avoir d'éléments k triés ?

Quelle va être la deuxième valeur prise par debut ? Combien va-t-on avoir d'éléments triés k dans le sous-tableau de droite ?

En déduire la relation entre le nombre de tours de boucle finalisé k et la valeur de la variable de boucle debut.

Correction ?

...CORRECTION...

POUR debut variant de 0 à (longueur - 1)

Lors du premier tour, debut vaut donc 0.

On cherche donc le minimum sur tout le tableau car on active minimum(tableau, 0).

Ensuite, on intervertit et on place donc ce minimum à l'index 0.

tableau[0] contient donc la plus petite valeur présente dans le tableau.

On voit donc qu'à la fin de la boucle avec debut à 0, on obtient 1 élément trié.

On peut donc écrire k = debut + 1.

Quelques exemples pour se convaincre de la formule.

Avant la boucle (k=0), il n'y a aucun élément trié.

Après le premier tour de boucle (celui où debut vaut 0) on a 1 élément trié : k = 1.

Après le deuxième tour de boucle (celui où debut vaut 1) on a 2 éléments triés : k = 2.

ect ...

On voit bien qu'on retrouve k = debut + 1.

Montrons maintenant la conservation.

On fait l'hypothèse de la véricité de P_k est vraie. Après k tours de boucle, le sous-tableau trié possède donc k éléments et nous avons donc

un sous-tableau d'éléments triés sur les index 0 à k-1 et
un sous-tableau non trié sur les index k et plus.

14° Montrer qu'avec un tour de boucle en plus, P_k implique que P_k+1 est vrai.

Correction ?

...CORRECTION...

Commençons par définir l'état du système à la fin de la boucle k.

A la fin de la boucle k, nous avions k éléments triés dans [0, k-1] et une variable debut contenant k-1 puisque k = debut + 1.

L'hypothèse de départ P_k implique donc que le sous-tableau de 0 à k-1 est trié.

Si on refait un tour de boucle, on incrémente debut qui passe à la valeur k.

On cherche donc l'élément à placer sur l'index k en cherchant le plus petit élément dans le sous-tableau non-trié [k, fin] à l'aide de la fonction minimum et à le placer sur l'index k.

On peut donc dire qu'à l'issue de ce tour de boucle :

Les éléments de 0 à k-1 sont toujours triés puisqu'on n'y touche pas !
L'élément sur l'index k est plus grand que ceux de 0 à k-1, sinon il aurait déjà été dans le sous-tableau trié.
Les éléments de 0 à k sont donc triés.

On vient donc bien de montrer la conservation de l'invariant à chaque tour de boucle.

On écrira donc P_k ➡ P_k+1

La dernière étape est ici assez rapide :

L'invariant P_k est la propriété selon laquel le sous-tableau [0; k-1] est trié.

Avec l'initialisation, nous avons montré que l'invariant P₀ est vrai avant la boucle POUR.

Avec la conservation, nous avons montré que l'invariant restait vrai après chaque tour de boucle.

Passons à la terminaison :

Nous avions remarquer qu'à la fin d'un tour de boucle, la relation entre k et la variable de boucle debut est k = debut + 1 :

A la fin du tour de boucle pour

debut valant 0, on a 1 élément trié (k vaut 1).
debut valant 1, on a 2 éléments triés (k vaut 2).
debut valant 2, on a 3 éléments triés (k vaut 3).
ect...

Or la boucle bornée POUR est POUR debut variant de 0 à (longueur - 1).

A la fin, debut vaut donc longueur - 1.

Le nombre k d'élément contenus dans le sous-tableau trié est donc
k = debut + 1
k = longueur - 1 + 1
k = longueur

Tout le tableau est donc bien trié puisque k correspond au nombre d'éléments triés.

Les réflexions ci-dessus permettent donc de prouver la correction de l'algorithme du tri par insertion.

Cet algorithme fonctionne donc dans tous les cas valides, c'est à dire tous les cas où l'ENTREE (le tableau) respecte bien les préconditions fournies.

5 - Python : Assertion de vérification

⇩ ⇧ ⤊

Nous allons finir en utilisant des assertions pour vérifier que notre invariant est bien un invariant valable.

Comme l'invariant est la propriété d'un sous-tableau d'être trié, nous allons créer une fonction est_trie qui vérifie cela.

On remarque bien la présence, ligne 25, d'une assertion à la fin de la boucle POUR de façon à vérifier si l'invariant est toujours vérifié.

import random as rd
 
serie1 = [rd.randint(0, 100) for x in range(20)]
 
def intervertir(tableau, i, j):
    """Procédure qui intervertit les valeurs stockées aux index a et b
 
    :: param tableau(list) :: un tableau non vide ne contenant que des entiers
    :: param i(int) :: un index valide pour le tableau
    :: param j(int) :: un autre indice valide
    :: return(None) :: "procédure"
 
    .. Effet de bord :: le tableau est modifié par effet de bord
    """
    temp = tableau[i]
    tableau[i] = tableau[j]
    tableau[j] = temp
 
def minimum(tableau, debut):
    """Renvoie l'index de la valeur minimale trouvé dans le sous-tableau commençant à l'index début
 
    :: param tableau(list) :: un tableau non vide ne contenant que des entiers
    :: param debut(int) :: un index valide pour le tableau
    :: return(int) :: renvoie l'index de la valeur minimale
 
    :: exemple ::
    >>> minimum([10,20,-50,100,20,12], 3)
    5
 
    """
    indice_minimum = debut  # Au début, on prend le premier élément, l'index debut, pas 0 !
    for index in range(debut+1, len(tableau)):
        if tableau[index] < tableau[indice_minimum]:
            indice_minimum = index
    return indice_minimum
 
def tri_selection(tableau):
    """Trie le tableau sur place en utilisant le tri par sélection
 
    :: param tableau(list) :: un tableau non vide ne contenant que des entiers
    :: return(None) :: "procédure"
 
    :: exemple ::
    >>> tab_test = [40,50,20]
    >>> tri_selection(tab_test)
    >>> tab_test
    [20, 40, 50]
 
    """
    for debut in range(len(tableau)):
        indice_min = minimum(tableau, debut)
        intervertir(tableau, debut, indice_min)
        assert est_trie(tableau, debut)
 
def est_trie(tableau,k):
    """Renvoie True si le sous-tableau [0;k] est trié dans l'ordre croissant"""
    if len(tableau) < 2:
        return True
    for index in range(k):
        if tableau[index] > tableau[index+1]:
            return False
    return True
 
if __name__ == '__main__':
    import doctest
    doctest.testmod()

15° Ligne 53 : que va-t-il se passer sur le sous-tableau [0;k]

est bien trié
est mal trié

Correction ?

...CORRECTION...

Si le tableau est bien trié, il ne se passe rien : l'assertion est vérifiée mais le système n'active rien de particulier.

Par contre, si l'assertion est évaluée à FAUX, une interruption (Exception) va stopper le programme et afficher le message fourni après la virgule.

16° Tester le programme avec les commandes suivantes pour vérifer que l'assertion n'active rien, ce qui prouve que l'invariant est bien constamment vérifié après chaque tour de boucle.


>>> serie1
[57, 73, 68, 46, 97, 61, 86, 15, 43, 32, 91, 92, 51, 35, 80, 95, 18, 96, 50, 93]
>>> tri_selection(serie1)
>>> serie1
[15, 18, 32, 35, 43, 46, 50, 51, 57, 61, 68, 73, 80, 86, 91, 92, 93, 95, 96, 97]

6 - FAQ

⇩ ⇧ ⤊

Pourquoi justifiez la terminaison d'une boucle FOR ?

Un peu pour l'exercice. Il existe deux cas où une boucle POUR peut mal tourner :

On demande par exemple de commencer à 1, de s'arrêter à 10 et de décrémenter de 1 à chaque tour. Ca donne 1, 0, -1 ... et ça ne s'arrêtera jamais...
On touche à la variable de boucle dans la boucle.

Ici, vous n'avez ni l'un ni l'autre mais ça vous permettra de vous souvenir qu'il faut un peu surveiller les boucles POUR quand même.

J'ai également vu O(log₂ n). C'est quoi ce truc ?

Il s'agit de la fonction logarithme (ici en base 2).

C'est une fonction extrêmement utile : on peut la voir en première approximation comme la fonction qui renvoie la puissance de 2 permettant d'écrire le nombre.

Quelques exemples avec Python


>>> import math
>>> math.log2(1)
0.0

Pourquoi ? Simplement car 1 = 2⁰. On renvoie 0.


>>> math.log2(2)
1.0

Pourquoi ? Simplement car 2 = 2¹. On renvoie 1.


>>> math.log2(4)
2.0

Pourquoi ? Simplement car 4 = 2². On renvoie 2.


>>> math.log2(8)
3.0

Pourquoi ? Simplement car 8 = 2³. On renvoie 3.

Le mieux, c'est que cela fonctionne également avec les valeurs qui ne sont pas une puissance entière de 2 !


>>> math.log2(6)
2.584962500721156

Pourquoi ? Simplement car 6 = 2^{2.584962500721156}. On renvoie 2.584962500721156. Si vous avez bien compris l'activité sur les floats, vous devriez comprendre qu'il s'agit certainement d'une valeur approximative.

Il existe un logarithme pour toutes les bases possibles et imaginables.

Le logarithme base 10 donne ainsi log10(1000) = 3 puisque 1000 = 10³

Ou encore le logarithme népérien ln qui est en lien avec la fonction exponentielle : ln(20) = 2.995732273553991 car on peut écrire

20 = e^{2.995732273553991} ou encore
20 = exp(2.995732273553991)

Et c'est lié au fait qu'avec un tableau de 1 million d'éléments, la méthode dichotomique ne prend qu'une vingtaine d'étapes au pire

Oui.


>>> math.log2(1E6)
19.931568569324174

Log et Lg, c'est différent ?

Oui.

Lorsqu'on parle simplement de log, on parle du log dans une base donnée. Si c'est rien n'est précisé, c'est certainement la base 10.

Habituellement, si on note juste log, on parle du log10.

Si on note lg(x), on parle de log₂(x) dans un contexte informatique. Cela évite de noter log₁₀(x). On note juste lg(x)

Attention donc au contexte dans lequel apparaît un logarithme.

Log et Ln, c'est différent ?

Oui.

Lorsqu'on parle simplement de log, on parle du log dans une base donnée. Si c'est rien n'est précisé, c'est certainement la base 10.

Lorsqu'on parle de ln, on parle du logarithme népérien en mathématiques. Vous le verrez en terminale.

Sauf que dans les documents informatiques, on parle souvent du logarithmique base 2. On devrait le noter log2 ou log₂. Mais souvent, la complexité ou le coût apparaît sous la forme lg (voir au dessous) mais aussi parfois ln. Pourquoi ? Tout simplement car log₂(x) = ln (x) / ln (2). ln 2 n'est donc qu'un coefficient multiplicateur. C'est un peu comme un coût en 0.5n³ qu'on noterait juste n³.

Attention donc au contexte dans lequel apparaît un logarithme.

Petit résumé des notations

On voit juste log : c'est certainement log₁₀.

On voit juste lg : c'est certainement log₂.

On voit juste ln : c'est le logarithme népérien.

Activité publiée le 01 09 2020
Dernière modification : 02 04 2023
Auteur : ows. h.

⏪

⏫

⏩

9 - Preuve du tri par sélection

1 - Rappel visuel du tri et algorithme

Algorithme de tri par sélection

Algorithme de minimum(tableau, debut)

Algorithme de intervertir(tableau, i, j)

2 - Preuve de terminaison

Rappel : Preuve de terminaison

3 - Coût du tri par sélection

Algortihme du tri par sélection

Algorithme de minimum(tableau, debut)

Complexité du tri par sélection

4 - Preuve de correction

Tests

Preuve de correction et invariant

Définitions

Démonstration en 3 phases : Initialisation-Conservation-Terminaison

Invariant du tri par sélection

Algorithme de tri par sélection

5 - Python : Assertion de vérification

6 - FAQ

J'ai également vu O(log2 n). C'est quoi ce truc ?

Et c'est lié au fait qu'avec un tableau de 1 million d'éléments, la méthode dichotomique ne prend qu'une vingtaine d'étapes au pire

Log et Lg, c'est différent ?

Log et Ln, c'est différent ?

Petit résumé des notations

Algorithme de `minimum(tableau, debut)`

J'ai également vu O(log₂ n). C'est quoi ce truc ?