14 - Chiffrement symétrique

⏪

⏬

⏩

1 - Code de César

2 - XOR

3 - FAQ

Nous avons vu que le Web utilise principalement deux protocoles :

le protocole HTTP où les paquets IP transitent de routeurs en routeurs en clair. N'importe qui possédant des droits sur les routeurs peut lire la communication s'il en a envie. Pas terrible pour les transmissions sensibles comme les mots de passe ou les numéros de carte bancaire.
le protocole HTTPS où les paquets IP transitent de routeurs en routeurs en étant chiffrés("cryptés"). Cette fois, même en étant interceptés, les paquets IP ne peuvent pas être compris. Ils peuvent être lus mais le contenu semblera totalement aléatoire et incompréhensible.

Dans cette partie, nous allons nous intéresser à ces techniques de chiffrement.

Evaluation ✎ : -

Documents de cours PDF : .PDF

Sources latex : .TEX, entete.tex et licence.tex

MODE COURS (cacher les questions)

1 - Le code de César

⇩ ⇧ ⤊

Le code de César n'est plus utilisé pour chiffrer (ou "crypter") les communications. Il est beaucoup trop simple à déchiffrer une fois qu'on connaît le principe.

Cette technique est basée sur un simple décalage des lettres.

Par exemple, on décale les lettres de 1 position vers la droite.

A devient B, B devient C... jusqu'à Z qui devient ... A.

Pourquoi César ?

César aurait utilisé un tel chiffrement pour sa correspondance.

Il utilisait un décalage de 3 lettres vers la droite en utilisant l'alphabet ... grec. Deux niveaux de difficultés pour les gens qui cherchaient à intercepter ses courriers.

Appliqué à notre alphabet, le décalage de 3 lettres donne ceci :

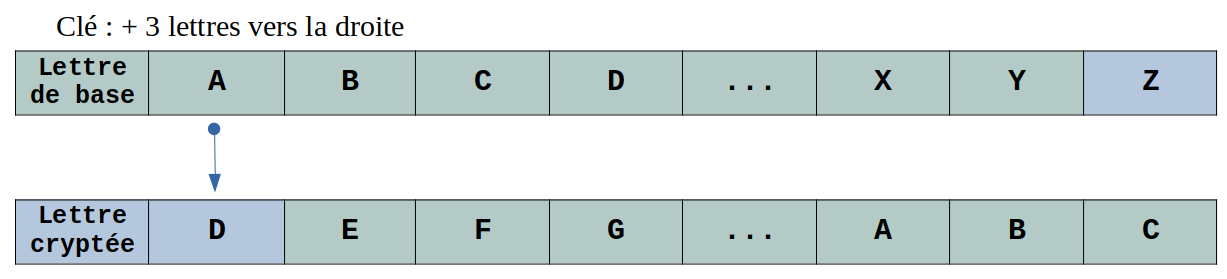
Commençons par voir comment nous pourrions décaler les lettres simplement avec un tableau contenant notre séquence de lettres.

01° Créer la fonction trouve_indice() qui renvoie l'indice de l'élément recherché dans le type construit fourni (un tableau, un tuple, un string). Si plusieurs éléments identiques se trouvent dans le tableau, on renvoie le plus petit. Si l'élément n'est pas présent, la fonction renvoie None.

Voici le prototype :

`1`	`trouve_indice(element:str, sequence:str\|list\|tuple) -> int\|None`

Exemple avec le tableau ALPHABET que vous pouvez visualiser en ligne 1.


>>> trouve_indice('A', ALPHABET)
0
 
>>> trouve_indice('B', ALPHABET)
1

Principe de l'algorithme : pour chaque valeur d'indice, lire l'élément correspondant. S'il correspond à l'élement cherché, on renvoie l'indice actuel.

ALPHABET = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z']
 
def trouve_indice(element, sequence):
    """Renvoie l'indice de element dans l'itérable sequence
 
    :: param element(str)              :: l'élément qu'on cherche à trouver
    :: param sequence(str|list|tuple)  :: un itérable contenant des éléments
    :: return (int|None)               :: l'indice de l'élément (ou None)
 
    >>> lettres = ['A', 'B', 'C', 'D', 'E', 'F']
    >>> trouve_indice('A', lettres)
    0
    >>> trouve_indice('C', lettres)
    2
    >>> trouve_indice('Z', lettres)
 
    """
    pass
 
if __name__ == '__main__':
    import doctest
    doctest.testmod()

Notez bien que dans le dernier exemple, la lettre Z n'apparaît pas dans la variable lettres. C'est pour cela que la fonction ne renvoie rien.

Correction ?

...CORRECTION...

ALPHABET = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z']
 
def trouve_indice(element, sequence):
    """Renvoie l'indice de element dans l'itérable sequence
 
    :: param element(str)              :: l'élément qu'on cherche à trouver
    :: param sequence(str|list|tuple)  :: un itérable contenant des éléments
    :: return (int|None)               :: l'indice de l'élément (ou None)
 
    >>> lettres = ['A', 'B', 'C', 'D', 'E', 'F']
    >>> trouve_indice('A', lettres)
    0
    >>> trouve_indice('C', lettres)
    2
    >>> trouve_indice('Z', lettres)
 
    """
    for i in range(len(sequence)):
        if sequence[i] == element:
            return i
 
if __name__ == '__main__':
    import doctest
    doctest.testmod()

On utilise un for associé à un return. Algorithmiquement, il aurait fallu plutôt utiliser un while. Mais le for+return rend le code plus intuitif à comprendre.

Voici la version avec un while :

ALPHABET = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z']
 
def trouve_indice(element:str, sequence:'str|list|tuple') -> 'int|None':
    """Renvoie l'indice de element dans l'itérable sequence"""
 
    i = 0
    while i < len(sequence) and sequence[i] != element:  # TQ l'indice existe et ne contient pas l'élément voulu 
        i = i + 1  # passe à la case suivante
 
    if i < len(sequence):  # si le i final est valide
        return i
 
    # si on arrive ici, c'est qu'on a dépassé la dernière case, on renvoie None

Comme la recherche d'un élément dans un tableau est une chose courante et que les tableaux sont des objets en Python, il existe déjà une méthode qui fait ce que nous venons de réaliser... Le but de la NSI est néanmoins de parvenir à construire vos propres fonctions avant d'utiliser trop de "boîtes noires" créées par d'autres personnes. Cette méthode n'est donc pas au programme. Pas plus que remove(), pop(0), sort()...

02° Tester les instructions suivantes pour vous persuader que la méthode des lists index() permet de faire (presque) la même chose que la fonction que nous venons de construire. Attention, ALPHABET devra être en mémoire lors de ce test.


>>> ALPHABET.index('A')
0
 
>>> ALPHABET.index('B')
1
 
>>> ALPHABET.index('Z')
25
 
>>> ALPHABET.index('a')

Questions :

avez-vous trouvé la différence qui existe entre cette façon de faire et la fonction que nous avions conçue ?
(hors programme) Comment pourrions-nous créer la fonction trouve_indice() en utilisant à l'interne la méthode index() ?

Correction ?

...CORRECTION...

La méthode index() déclenche une erreur si l'élément n'existe pas.

ALPHABET = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z']
 
def trouve_indice(element:str, sequence:'str|list|tuple') -> 'int|None':
    """Renvoie l'indice de element dans l'itérable sequence"""
 
    try:                                   # Tente
        reponse = sequence.index(element)  # d'utiliser index()
    except:                                # et si cela déclenche une exception
        reponse = None                     # affecte reponse avec None
 
    return reponse

Une fois qu'on a trouvé l'indice de la lettre dans l'alphabet, il suffit de rajouter la clé et on obtient alors le chiffrement qui remplace cette lettre.

Ainsi avec une clé de 3 et une lettre B : l'indice de B est 1, on lui ajoute 3 et on obtient ainsi l'indice 4. Il suffit de renvoyer la lettre située à cet indice : E.

Comme nous allons toujours travailler à priori avec le tableau constant ALPHABET, j'ai rajouté ,en ligne 1 ci-dessous, cette valeur par défaut à ce paramètre. Cela nous évitera de le fournir à chaque fois.

03° Tester maintenant la fonction decale() qui renvoie une lettre présente dans alphabet en la décalant de cle position vers la droite.

Laissez les variables et fonctions précédentes dans script.

PRECONDITION : l'élément est bien présent dans la séquence.

def decale(element, cle, sequence=ALPHABET):
    """Renvoie la lettre chiffrée en décalant de cle case vers la droite (element doit être présent dans sequence)"""
    indice = trouve_indice(element, sequence)
    indice_decale = indice + cle
    return sequence[indice_decale]

Vous pourriez tester des appels comme ceux-ci :


>>> decale(element='A', cle=3)
>>> decale(element='B', cle=3)
>>> decale(element='C', cle=3)
>>> decale(element='W', cle=3)
>>> decale(element='X', cle=3)

Qu'est-ce qui provoque l'erreur qui survient parfois ?

Correction ?

...CORRECTION...

La fonction semble bien fonctionner sauf pour X et plus...

Pourquoi ? Simplement car l'indice de X vaut 23. Or 23 + 3 = 26.

Notre tableau n'ayant des indices valides que dans l'intervalle [0, 25], les lettres X, Y et Z provoquent une demande hors indice.

Pour éviter ce problème, il faut parvenir à faire comprendre à la machine qu'après l'indice 25, on veut l'indice 0.

Ainsi, si on obtient l'indice 23 du 'X' et qu'on rajoute 3, on obtient 26 mais on veut en réalité obtenir 0 pour 'A'.

Pour 'Y' (24), on obtient 24+3=27 mais on veut 'B' (indice 1).

Comment faire ? Utiliser le modulo !

Rappel :


>>> 24 % 26
24
 
>>> 25 % 26
25
 
>>> 26 % 26
0
 
>>> 27 % 26
1
 
>>> 28 % 26
2

04° Modifier decale() pour qu'elle gère bien les recherches dépassant l'indice maximum.


>>> decale(element='W', cle=3)
'Z'
 
>>> decale(element='X', cle=3)
'A'
 
>>> decale(element='Y', cle=3)
'B'

Correction ?

...CORRECTION...

def decale(element, cle, sequence=ALPHABET):
    """Renvoie la lettre chiffrant la lettre element en décalant de cle case vers la droite"""
    indice = trouve_indice(element, sequence)
    indice_decale = (indice + cle) % len(sequence)
    return sequence[indice_decale]

Le problème du code de César est qu'il ne gère pas tous les caractères : on ne travaille qu'avec des lettres majuscules non accentuées ou autres. On acceptera certains caractères de ponctuation qu'on ne modifiera pas d'ailleurs.

05° Expliquer de la façon la plus précise possible comment fonctionne la fonction filtre(). On rappelle que le string Python est une structure de données non mutable et qu'on doit donc recréer un string lorsqu'on veut en "modifier" un.

# Constantes
 
ALPHABET = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z']
PONCTUATION = [' ', '.', '!', '?', ',', "'", ' ']
 
# Déclaration des fonctions
 
def filtre(message:str) -> str:
    """Renvoie un string où les lettres sont toutes en majuscules"""
    message = message.upper()   # Méthode des strings qui renvoie les lettres en majuscules
    reponse = ''                # on va créer un string de réponse progressivement : on l'initialise
    for caractere in message:
        if caractere in ALPHABET or caractere in PONCTUATION :
            reponse = reponse + caractere   # on ne le garde que s'il fait partie d'un des 2 tableaux
    return reponse
 
# Instructions du programme principal
 
if __name__ == '__main__':
    message = "L'épreuve est au mois de mars, vraiment ?"

Expliquer ensuite pourquoi on obtient la réponse suivante en lançant la fonction avec la variable message.


>>> message
"L'épreuve est au mois de mars, vraiment ?"
 
>>> mess_filtre = filtre(message)
>>> mess_filtre
"L'PREUVE EST AU MOIS DE MARS, VRAIMENT ?"

Nous allons maintenant nous intéresser au chiffrement de la chaîne de caractères filtrée qui ne contient donc que des caractères compatibles avec la fonction chiffrement().

Voici le code du projet en l'état. Il reprend les fonctions réalisées plus haut (trouve_indice(), decale() et filtre()) mais rajoute la fonction chiffrement() qui va permettre d'agir sur toute une chaîne de caractères, pas uniquement sur un seul caractère à la fois.

Pour gagner quelques lignes, j'ai décidé d'utiliser la forme de documentation courte pour les trois fonctions déjà étudiées.

06° Mettre le code ci-dessous en mémoire. Utiliser les instructions suivantes pour visualiser son fonctionnement.


>>> message
"L'épreuve est au mois de mars, vraiment ?"
 
>>> message = filtre(message)
>>> message
"L'PREUVE EST AU MOIS DE MARS, VRAIMENT ?"
 
>>> mc = chiffrement(message, 3)
>>> mc
"O'SUHXYH HVW DX PRLV GH PDUV, YUDLPHQW ?"
 
>>> mc = chiffrement(message, 3, debug=True)
L devient O
P devient S
R devient U
E devient H
U devient X
V devient Y
E devient H
E devient H
S devient V
T devient W
A devient D
U devient X
M devient P
O devient R
I devient L
S devient V
D devient G
E devient H
M devient P
A devient D
R devient U
S devient V
V devient Y
R devient U
A devient D
I devient L
M devient P
E devient H
N devient Q
T devient W

"""Permet de gérer le chiffrement par code de César.
 
Fonctions 
---------
 
1 :: trouve_indice(element:str, sequence:list=ALPHABET) -> int
2 :: decale(element:str, cle:int, sequence:list=ALPHABET) -> str
3 :: filtre(message:str) -> str
4 :: chiffrement(message:str, cle:int, sequence:list=ALPHABET, ponctuation:list=PONCTUATION, debug:bool=False)
 
"""
# Constantes
 
ALPHABET = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z']
PONCTUATION = [' ', '.', '!', '?', ',', "'", ' ']
 
 
# Déclarations des fonctions
 
def trouve_indice(element:str, sequence:list=ALPHABET) -> 'int|None':
    """Renvoie l'indice de element dans le tableau sequence """
    for indice in range(len(sequence)):
        if sequence[indice] == element:
            return indice
 
def decale(element:str, cle:int, sequence:list=ALPHABET) -> str:
    """Renvoie la lettre chiffrée en décalant de cle case vers la droite (element doit être présent dans sequence)"""
    indice = trouve_indice(element, sequence)
    indice_decale = (indice + cle) % len(sequence)
    return sequence[indice_decale]
 
def filtre(message:str) -> str:
    """Renvoie un string où les lettres sont toutes en majuscules"""
    message = message.upper()   # Méthode des strings qui renvoie les lettres en majuscules
    reponse = ''                # on va créer un string de réponse progressivement : on l'initialise
    for caractere in message:
        if caractere in ALPHABET or caractere in PONCTUATION :
            reponse = reponse + caractere   # on ne le garde que s'il fait partie d'un des 2 tableaux
    return reponse
 
def chiffrement(message, cle, sequence=ALPHABET, ponctuation=PONCTUATION, debug=False):
    """Renvoie un string en décalant les lettres majuscules de cle rangs vers la droite
 
    :: param message(str)      :: un string filtré ne contenant que des majuscules ou de la ponctuation
    :: param cle(int)          :: la valeur entière du décalage vers la droite pour crypter
    :: param sequence(list)    :: la séquence des caractères cryptables
    :: param ponctuation(list) :: la séquence des caractères inchangées lors du chiffrement 
    :: return (str) :: le string crypté
 
    :: exemple :: 
    >>> chiffrement("ABCé D,XYZ", 3)
    'DEF G,ABC'
 
    """
    reponse = ''
    for caractere in message:
        if caractere in ponctuation:
            reponse = reponse + caractere
        elif caractere in sequence:
            crypte = decale(caractere, cle)
            reponse = reponse + crypte
            if debug: print(f"{caractere} devient {crypte}")
    return reponse
 
 
# Instructions du programme principal
 
if __name__ == '__main__':
    import doctest
    doctest.testmod()
    message = "L'épreuve est au mois de mars, vraiment ?"

07° Expliquer de la façon la plus précise possible comment fonctionne la fonction chiffrement(). On rappelle que le string est en Python une structure de données non mutable et qu'on doit donc recréer un string lorsqu'on veut en "modifier" un.

08° Réaliser la fonction dechiffrement() qui doit pouvoir retrouver le texte de base si on lui fournit le texte chiffré et la clé de chiffrement en entrée.

PRECONDITION : le message chiffré ne doit contenir que des caractères présents dans les paramètres sequence et ponctuation.

def dechiffrement(message, cle, sequence=ALPHABET, ponctuation=PONCTUATION, debug=False):
    """Renvoie un string en décalant les lettres majuscules de cle rangs vers la droite
 
    :: param message(str)      :: un string chiffré ne contenant que des majuscules ou de la ponctuation
    :: param cle(int)          :: la valeur entière du décalage vers la droite pour crypter
    :: param sequence(list)    :: la séquence des caractères chiffrables
    :: param ponctuation(list) :: la séquence des caractères inchangées lors du chiffrement 
    :: return (str) :: le string crypté
 
    :: exemple :: 
    >>> dechiffrement('DEF G,ABC', 3)
    'ABC D,XYZ'
 
    """
    pass

Exemple d'utilisation (mc veut dire message crypté et md message décrypté)


>>> message = filtre(message)
>>> message
"L'PREUVE EST AU MOIS DE MARS, VRAIMENT ?"
 
>>> mc = chiffrement(message, 3)
>>> mc
"O'SUHXYH HVW DX PRLV GH PDUV, YUDLPHQW ?"
 
>>> md = dechiffrement(mc, 3)
>>> md
"L'PREUVE EST AU MOIS DE MARS, VRAIMENT ?"

Correction ?

...CORRECTION...

def dechiffrement(message, cle, sequence=ALPHABET, ponctuation=PONCTUATION, debug=False):
    """Renvoie un string en décalant les lettres majuscules de cle rangs vers la droite
 
    :: param message(str)      :: un string chiffré ne contenant que des majuscules ou de la ponctuation
    :: param cle(int)          :: la valeur entière du décalage vers la droite pour crypter
    :: param sequence(list)    :: la séquence des caractères cryptables
    :: param ponctuation(list) :: la séquence des caractères inchangées lors du chiffrement 
    :: return (str) :: le string crypté
 
    :: exemple :: 
    >>> dechiffrement('DEF G,ABC', 3)
    'ABC D,XYZ'
 
    """
    reponse = ''
    for caractere in message:
        if caractere in ponctuation:
            reponse = reponse + caractere
        elif caractere in sequence:
            crypte = decale(caractere, -cle)
            reponse = reponse + crypte
            if debug: print(f"{caractere} devient {crypte}")
    return reponse

chiffrement symétrique

Une méthode de chiffrement est dite symétrique lorsqu'on a besoin de la même clé pour chiffrer ou déchiffrer le message. Les deux personnages voulant communiquer doivent donc partager une clé commune.

Si quelqu'un intercepte la communication, il ne pourra lire que le message chiffré.

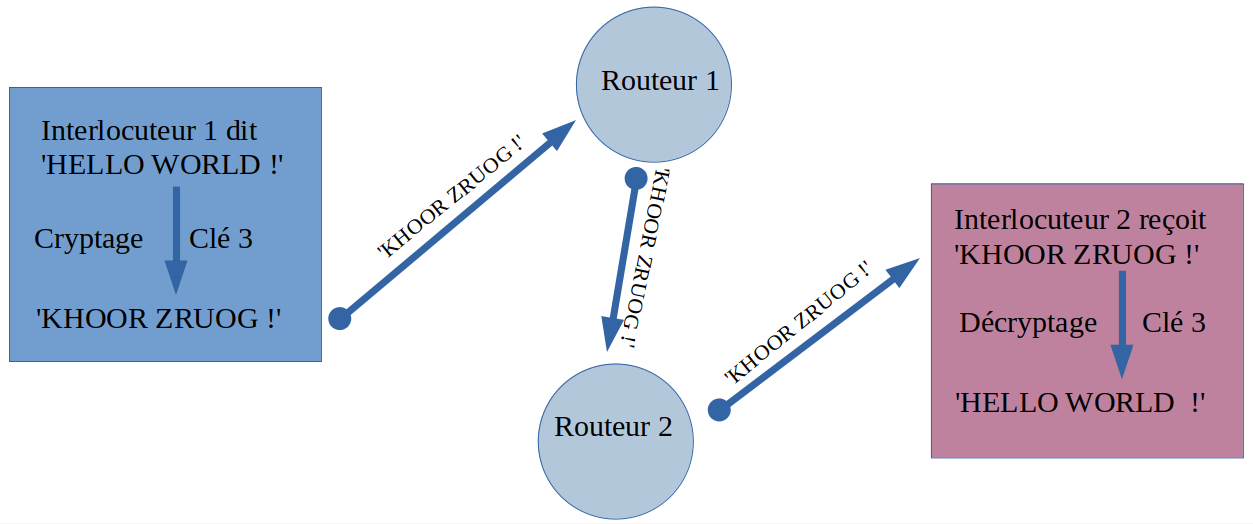
Il est possible qu'on doive utiliser différemment cette clé lors de la phase de chiffrement et lors de la phase de déchiffrement mais la clé est bien la même dans les deux cas.

Initialisation

Les deux personnes qui désirent communiquer doivent donc partager cette clé à un moment ou à un autre AVANT de pouvoir communiquer de façon chiffrée.

Si cet échange se fait physiquement, les deux personnes pourront alors communiquer à distance en utilisant cette clé.

Deux problèmes émergent donc avec cette technique de chiffrement symétrique :

Le chiffrement doit être assez complexe pour qu'on ne puisse pas retrouver le message d'origine en un temps raisonnable (soit par force brute, soit en utilisant une faille permettant de limiter le vrai nombre de clés valides). Ce n'est pas le cas par exemple avec le code de César puisqu'il n'y a que 25 permutations possibles.
On ne peut pas initier une telle communication à distance entre deux inconnus : ils devraient se mettre d'accord à distance sur la clé en la communiquant en clair : on pourrait alors très bien intercepter la clé envoyée en clair puis continuer à écouter les messages chiffrés en les déchiffrant puisqu'on connaît la valeur de la clé, interceptée en clair !

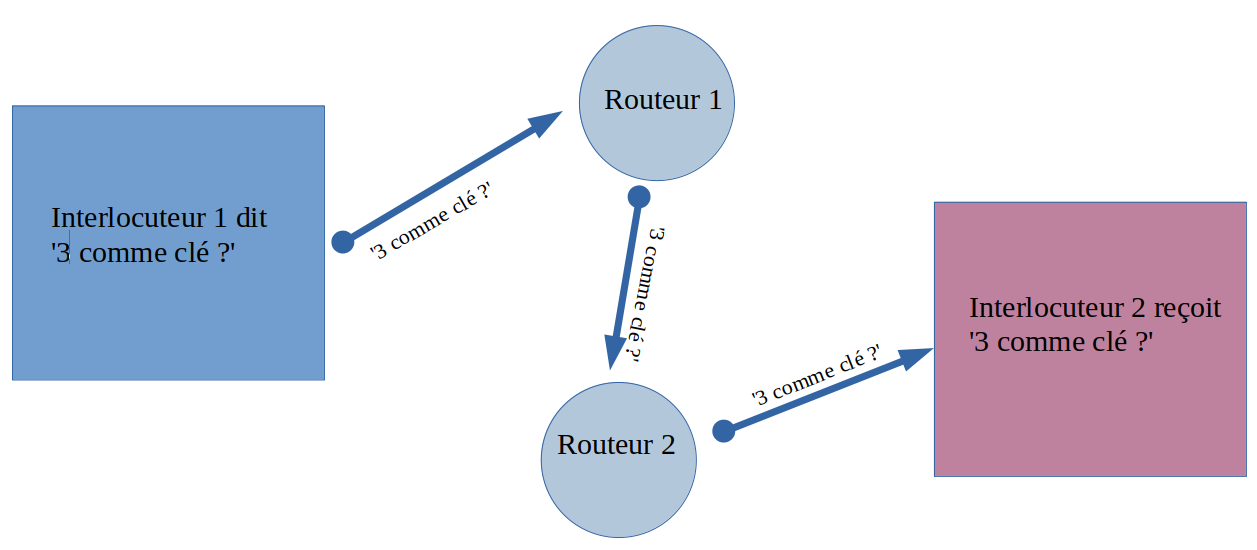
L'échange en clair d'une clé symétrique est donc dangereux et stupide : le but est de garantir la confidentialité de l'échange. S'il suffit d'écouter le premier échange pour parvenir à pénétrer la protection... Autant ne rien faire.

Nous verrons dans la prochaine activité comment parvenir à échanger cette clé symétrique de façon sécurisée.

09° Le chiffrement de César est-il une solution symétrique ou asymétrique. Justifier.

Correction ?

...CORRECTION...

Symétrique puisqu'on utilise la même clé pour la fonction de chiffrement et la fonction de déchiffrement.

10° Combien de clés sont-elles possibles ici ? Ce système est-il résistant à une recherche par force brute ?

Correction ?

...CORRECTION...

Il n'y a que 26 combinaisons avec nos 26 lettres : on peut décaler de 0 à 25 cases. Et encore, le cas 0 est un peu stupide : on ne décale pas...

Bref, 25 valeurs de clé à tester. Non, ce système n'est pas utilisable pour un chiffrement réel.

Chiffrement ou cryptage ?

Puisqu'on stocke tout sous forme d'octets, on parle en réalité plutôt de chiffrement puisqu'on peut toujours interpréter un octet comme un nombre compris entre 0 et 255.

Rappel : un octet correspond à 8 bits.

Il y a donc 2⁸ valeurs possibles (256).

Un octet permet donc d'obtenir des entiers naturels compris entre 0 et 255.

Chiffrement est donc synonyme de cryptage puisqu'on transforme en réalité une donnée en nombre et qu'on transforme ce nombre.

Si on prend le code de César, on pourrait utiliser la simple table ASCII :

A encodé en octet valant 65. Le 65 est transformé en 65 + 3 = 68.
Lors du déchiffrement, on récupère le 68 et on obtient 68 - 3 = 65. Un A.

2 - XOR bit à bit

⇩ ⇧ ⤊

Intéressons nous maintenant à une méthode permettant d'obtenir une meilleure résistance à la force brute.

Imaginons qu'on désire transmettre le message "ABC".

Ce n'est pas cette chaîne de caractères qui transite sur les routeurs mais uniquement la représentation en octets de celle-ci.

Voici la table ASCII complète, en version hexadécimale. Comme je ne suis pas méchant, vous pouvez visualiser la valeur décimale d'un caractère en stabilisant la souris au dessus du caractère.

Table ASCII en version hexadécimale

	_0	_1	_2	_3	_4	_5	_6	_7	_8	_9	_A	_B	_C	_D	_E	_F
0_	NUL	SOH	STX	ETX	EOT	ENQ	ACK	BEL	BS	HT	LF	VT	FF	CR	SO	SI	_0
1_	DLE	DC1	DC2	DC3	DC4	NAK	SYN	ETB	CAN	EM	SUB	ESC	FS	GS	RS	US	1_
2_		!	"	#	$	%	&	'	(	)	*	+	,	-	.	/	2_
3_	0	1	2	3	4	5	6	7	8	9	:	;	<	=	>	?	3_
4_	@	A	B	C	D	E	F	G	H	I	J	K	L	M	N	O	4_
5_	P	Q	R	S	T	U	V	W	X	Y	Z	[	\	]	^	_	5_
6_	`	a	b	c	d	e	f	g	h	i	j	k	l	m	n	o	6_
7_	p	q	r	s	t	u	v	w	x	y	z	{	\|	}	~	DEL	7_
	_0	_1	_2	_3	_4	_5	_6	_7	_8	_9	_A	_B	_C	_D	_E	_F

11° Répondre aux questions suivantes :

Donner la valeur des trois octets qui encodent notre message, en décimal.
Idem en hexadécimal.
Réaliser à la main la conversion de A de l'hexadécimal en décimal pour vous convaincre qu'il s'agit bien de la même valeur représentée de deux façons différentes.
Demander à Python de convertir la valeur hexadécimale de A en décimal.
Demander à Python de convertir la valeur décimale de A en hexadécimal.

Correction ?

...CORRECTION...

En décimal : 65 pour A, 66 pour B et 67 pour C.
En hexadécimal : 41 pour A, 42 pour B et 43 pour C.
41₁₆ = 4*16 + 1*1 = 65.
En Python : hexadécimal vers décimal


>>> 0x41
65

En Python : décimal vers hexadécimal


>>> hex(65)
'0x41'

Nous allons donc envoyer trois octets : 65, 66 et 67 en base 10.

12° Exprimer maintenant vos octets sous forme binaire : donner la suite de bits qui sera envoyé.

Correction ?

...CORRECTION...

65 donne 0100 0001₂, soit 64 + 1.

66 donne 0100 0010₂, soit 64 + 2.

67 donne 0100 0011₂, soit 64 + 2 + 1.

Pour obtenir cette décomposition avec Python :


>>> bin(65)
'0b1000001'

Zut, il y a un 0b au début de la réponse...

Pour supprimer les deux premiers caractères (0b) :


>>> bin(65)[2:]
'1000001'

Zut, il n'y a pas 8 caractères.

Pour imposer 8 caractères :


>>> f"{bin(65)[2:]:8}"
'1000001 '

Zut, il y a 8 caractères mais justifiés à gauche...

Pour justifier à droite :


>>> f"{bin(65)[2:]:>8}"
' 1000001'

Zut, il y a 8 caractères justifiés à droite mais avec un espace. Je veux mon 0 moi...

Pour justifier à droite ET rajouter les 0 nécessaires à gauche :


>>> f"{bin(65)[2:]:0>8}"
'01000001'

Enfin...

Maintenant que nous avons notre message binaire, regardons comment le chiffrer.

13° Compléter (vous pouvez cliquer sur les cases notées ?) la table de vérité du ET(AND), du NON-ET(NAND), du OU(OR) et du NON-OU(NOR) :

Rappel :

ET est évalué à VRAI si toutes les conditions sont vraies
OU est évalué à VRAI si l'une des conditions est vraie

NAND et NOR sont juste des inversions des réponses du AND et du OR.

a	b	a ET b	a NAND b
FAUX	FAUX	?	?
FAUX	VRAI	?	?
VRAI	FAUX	?	?
VRAI	VRAI	?	?

Pour le ET, cela revient à chercher cela avec Python :

a and b

Cela revient à chercher cela avec Javascript, C, C++ :

a && b

a	b	a OR b	a NOR b
FAUX	FAUX	?	?
FAUX	VRAI	?	?
VRAI	FAUX	?	?
VRAI	VRAI	?	?

Pour le OU, cela revient à chercher cela avec Python :

a or b

Cela revient à chercher cela avec Javascript, C, C++ :

a || b

Correction ?

...CORRECTION...

Pour le AND et le NAND

a	b	a ET b	a NAND b
FAUX	FAUX	FAUX	VRAI
FAUX	VRAI	FAUX	VRAI
VRAI	FAUX	FAUX	VRAI
VRAI	VRAI	VRAI	FAUX

Pour le OU et le NOR :

a	b	a OR b	a NOR b
FAUX	FAUX	FAUX	VRAI
FAUX	VRAI	VRAI	FAUX
VRAI	FAUX	VRAI	FAUX
VRAI	VRAI	VRAI	FAUX

14° Compléter la table de vérité du XOR (OU eXclusif) en utilisant simplement le rappel suivant : un OU eXclusif diffère du OU car il n'est évalué à VRAI que si l'une des expressions est VRAIE. Si deux expressions sont vraies, il est évaluée à FAUX.

a	b	a XOR b
0	0	?
0	1	?
1	0	?
1	1	?

Correction ?

...CORRECTION...

a	b	a XOR b
0	0	0
0	1	1
1	0	1
1	1	0

Nous allons utiliser le XOR entre les bits de nos messages et les bits de la clé commune choisie. Vous allez voir qu'on obtient alors un chiffrement efficace et que le déchiffrement se fait avec la même clé.

Imaginons que notre message soit "ABC" (65-66-67) et notre clé soit "D" (68, donc 0100 0100).

Voici le contenu binaire du message, suivi du contenu binaire de la clé.


Message m    : 01000001 01000010 01000011
Cle c        : 01000100

Pour obtenir le message crypté mc à partir du message et de la clé, nous allons simplement écrire m XOR c entre chacun des bits de m et de c.

Pour rappel, voici la table du XOR.

a	b	a XOR b
0	0	0
0	1	1
1	0	1
1	1	0

Premiers bits : 0 XOR 0 donne 0 car il n'y a pas une condition unique vraie.


Message m                   : 01000001 01000010 01000011
Cle c                       : 01000100
Message crypté mc = m XOR c : 0

Les bits suivants : 1 XOR 1 donne 0 car deux conditions vraies : on en veut une seule.


Message m                   : 01000001 01000010 01000011
Cle c                       : 01000100
Message crypté mc = m XOR c : 00

Les bits suivants : 1 XOR 1 donne 0 car deux conditions vraies : on en veut une seule.


Message m                   : 01000001 01000010 01000011
Cle c                       : 01000100
Message crypté mc = m XOR c : 000

15° Trouver les bits du premier octet du message chiffré. Que vaut-il ? Si on ouvrait le fichier chiffré comme un simple fichier texte en ASCII, à quel caractère correspond-t-il ?

Correction ?

...CORRECTION...


Message m                   : 01000001 01000010 01000011
Cle c                       : 01000100
Message crypté mc = m XOR c : 00000101

On obtient donc un octet "valant" 5.

Cela correspondrait à un caractère non imprimable exprimant une demande sur le réseau (ENQ, ENQUIRY).

Comment faire avec les octets suivants ? La clé n'est pas assez longue...

La solution retenue est simple : on copie-colle la clé autant de fois que nécessaire.


Message m                   : 01000001 01000010 01000011
Cle c                       : 01000100 01000100 01000100
Message crypté mc = m XOR c : 00000101

16° Déterminer maintenant le message chiffré complet, sous forme binaire puis en exprimant chaque octet en décimal.

Correction ?

...CORRECTION...


Message m                   : 01000001 01000010 01000011
Cle c                       : 01000100 01000100 01000100
Message crypté mc = m XOR c : 00000101 00000110 00000111

On obtient le message crypté suivant :

00000101 00000110 00000111

5 6 7

L'émetteur veut donc envoyer "ABC", qui correspond aux bits 01000001 01000010 01000011 (65-66-67) mais il va envoyer 00000101 00000110 00000111 (5-6-7).

Comment fait alors le récepteur pour décoder le message crypté ? C'est là toute la beauté du chiffrement en XOR : il suffit de refaire la même chose : on applique un XOR bit à bit entre le message chiffré et la clé.

17° Vous êtes le récepteur. Vous venez de recevoir le message indiqué. Vous savez que la clé commune est 0000 0101. Déchiffrer le message émis. Retrouve-t-on le 'ABC' initial en utilisant la même valeur de clé pour le déchiffrement et le chiffrement ?


Message crypté mc           : 00000101 00000110 00000111
Cle c                       : 01000100
Message m = mc XOR c        :

Correction ?

...CORRECTION...


Message crypté mc           : 00000101 00000110 00000111
Cle c                       : 01000100 01000100 01000100
Message m = mc XOR c        : 01000001 01000010 01000011

On retrouve bien la suite 65 - 66 - 67.

S'il s'agit d'un texte en ASCII, c'est bien "ABC".

18° La technique de chiffrement par XOR est-elle un chiffrement symétrique ou asymétrique ? La clé est-elle commune, partagée entre émetteur et récepteur.

Correction ?

...CORRECTION...

Même clé pour chiffrer/crypter/coder et déchiffrer/décrypter/décoder.

Il s'agit donc d'un chiffrement symétrique.

Par définition même, la clé est donc commune ou partagée.

19° Si votre clé fait 8 bits, combien y-a-t-il de combinaisons possibles à tester ? Si votre clé fait 128 bits, combien chiffrement peut-il résister à une recherche par force brute ?

Correction ?

...CORRECTION...

8 bits : 2⁸ possibilités : soit 256 clés à tester.

128 bits : 2¹²⁸ possibilités : soit 340282366920938463463374607431768211456 clés à tester.

20° Choisir une valeur-clé de 5 bits avec un autre étudiant. Transmettez lui un message codé 3 caractères-octets (48 bits) chiffré avec votre clé. Vérifier que les deux parties parviennent bien à communiquer correctement.

Pourquoi 5 bits et 48 bits? Car vous allez devoir faire un copier-coller non complet de la clé sur le dernier octet. Ce n'est pas grave.

Exemple avec un message de 12 bits et un clé de 5 bits.


Message m                   : 01000001 0100
Cle c                       : 11001
Message crypté mc = m XOR c :


Message m                   : 01000001 0100
Cle c                       : 11001110 0111
Message crypté mc = m XOR c :

Vous allez voir qu'à la main, c'est long... D'où le prochain mini-projet.

Correction ?

...CORRECTION...


Message m                   : 01000001 0100
Cle c                       : 11001110 0111
Message crypté mc = m XOR c : 10001111 0011

On envoie donc sur le réseau le message crypté suivant : 10001111 0011.

Le récepteur reçoit ce message sur sa machine.

Il doit alors utiliser un XOR bit à bit entre le message crypté et la clé partagée.


Message m                   : 10001111 0011
Cle c                       : 11001110 0111
Message crypté mc = m XOR c : 01000001 0100

Le message décrypté est bien identique au message initial.

3 - FAQ

⇩ ⇧ ⤊

Nous avions vu que créer un string par concaténation successive ce n'est pas très malin...

VOIR

C'est vrai !

Le coût de la création par concaténation est linéaire par rapport à n, le nombre de caractères.

Et donc, si vous concaténer ici un caractère à la fois à votre string qui devient peu à peu de plus en plus grand, cela donne ce coût :

𝞗(1 + 2 + 3 +.... n) opérations.

Il faut alors se souvenir de la formule d'Euler :

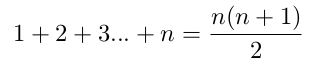
On peut également écrire cette formule ainsi :

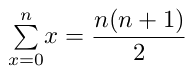
𝞗(1 + 2 + 3 +.... n)

= 𝞗( n*(n+1) / 2 )

= 𝞗( n*(n+1) )

= 𝞗( n*n )

= 𝞗( n² )

Le coût est donc QUADRATIQUE en n, le nombre final de caractères.

Et on fait comment alors ?

VOIR

On transtype le string en tableau avec la fonction list(). Cette phase a un coût linéaire.
On modifie les éléments du tableau, à coût constant pour chaque case puisque le tableau est mutable. Si on modifie toutes les cases, on obtient alors un coût linéaire pour cette phase.
On transtype le tableau en string avec la méthode join(), ce qui se fait à coût linéaire.

3 phases linéaires, donc une transformation globale à coût linéaire.

Quelques exemples d'utilisation de tout cela avant de vous montrer la nouvelle fonction filtre() :


>>> caracteres = list("Bonjour")
>>> caracteres
['B', 'o', 'n', 'j', 'o', 'u', 'r']
 
>>> valeurs = [ord(c) for c in caracteres]
>>> valeurs
[66, 111, 110, 106, 111, 117, 114]
 
>>> "*".join(caracteres)
'B*o*n*j*o*u*r'
 
>>> "".join(caracteres)
'Bonjour'
 
>>> "...".join(caracteres)
'B...o...n...j...o...u...r'

Voici une fonction de filtrage linéaire et non plus quadratique :

# Constantes
 
ALPHABET = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z']
PONCTUATION = [' ', '.', '!', '?', ',', "'", ' ']
 
# Déclaration des fonctions
 
def filtre(message:str) -> str:
    """Renvoie un string où les lettres sont toutes en majuscules"""
	 
	# 1 - On place tout le message en majuscules (linéaire)
    message = message.upper()   
	 
	# 2 - Transtype str -> list en ne gardant que les caractères acceptés (linéaire)
    caracteres = [c for c in message if c in ALPHABET or c in PONCTUATION]
	 
	# 3 - Transtype list -> str (linéaire)
    return "".join(caracteres)
 
# Instructions du programme principal
 
if __name__ == '__main__':
    message = "L'épreuve est au mois de mars, vraiment ?"
	mess_filtre = filtre(message)
	print(mess_filtre)	

Activité publiée le 02 10 2020
Dernière modification : 02 10 2020
Auteur : ows. h.

⏪

⏫

⏩

	_0	_1	_2	_3	_4	_5	_6	_7	_8	_9	_A	_B	_C	_D	_E	_F
0_	NUL	SOH	STX	ETX	EOT	ENQ	ACK	BEL	BS	HT	LF	VT	FF	CR	SO	SI	_0
1_	DLE	DC1	DC2	DC3	DC4	NAK	SYN	ETB	CAN	EM	SUB	ESC	FS	GS	RS	US	1_
2_		!	"	#	$	%	&	'	(	)	*	+	,	-	.	/	2_
3_	0	1	2	3	4	5	6	7	8	9	:	;	<	=	>	?	3_
4_	@	A	B	C	D	E	F	G	H	I	J	K	L	M	N	O	4_
5_	P	Q	R	S	T	U	V	W	X	Y	Z	[	\	]	^	_	5_
6_	`	a	b	c	d	e	f	g	h	i	j	k	l	m	n	o	6_
7_	p	q	r	s	t	u	v	w	x	y	z	{	\|	}	~	DEL	7_
	_0	_1	_2	_3	_4	_5	_6	_7	_8	_9	_A	_B	_C	_D	_E	_F

	_0	_1	_2	_3	_4	_5	_6	_7	_8	_9	_A	_B	_C	_D	_E	_F
0_	NUL	SOH	STX	ETX	EOT	ENQ	ACK	BEL	BS	HT	LF	VT	FF	CR	SO	SI	_0
1_	DLE	DC1	DC2	DC3	DC4	NAK	SYN	ETB	CAN	EM	SUB	ESC	FS	GS	RS	US	1_
2_		!	"	#	$	%	&	'	(	)	*	+	,	-	.	/	2_
3_	0	1	2	3	4	5	6	7	8	9	:	;	<	=	>	?	3_
4_	@	A	B	C	D	E	F	G	H	I	J	K	L	M	N	O	4_
5_	P	Q	R	S	T	U	V	W	X	Y	Z	[	\	]	^	_	5_
6_	`	a	b	c	d	e	f	g	h	i	j	k	l	m	n	o	6_
7_	p	q	r	s	t	u	v	w	x	y	z	{	\|	}	~	DEL	7_
	_0	_1	_2	_3	_4	_5	_6	_7	_8	_9	_A	_B	_C	_D	_E	_F

	_0	_1	_2	_3	_4	_5	_6	_7	_8	_9	_A	_B	_C	_D	_E	_F
0_	NUL	SOH	STX	ETX	EOT	ENQ	ACK	BEL	BS	HT	LF	VT	FF	CR	SO	SI	_0
1_	DLE	DC1	DC2	DC3	DC4	NAK	SYN	ETB	CAN	EM	SUB	ESC	FS	GS	RS	US	1_
2_		!	"	#	$	%	&	'	(	)	*	+	,	-	.	/	2_
3_	0	1	2	3	4	5	6	7	8	9	:	;	<	=	>	?	3_
4_	@	A	B	C	D	E	F	G	H	I	J	K	L	M	N	O	4_
5_	P	Q	R	S	T	U	V	W	X	Y	Z	[	\	]	^	_	5_
6_	`	a	b	c	d	e	f	g	h	i	j	k	l	m	n	o	6_
7_	p	q	r	s	t	u	v	w	x	y	z	{	\|	}	~	DEL	7_
	_0	_1	_2	_3	_4	_5	_6	_7	_8	_9	_A	_B	_C	_D	_E	_F