17 - Projet RSA

⏪

⏬

⏩

1 - principe

2 - RSA

3 - clés RSA

4 - Python-0

5 - Etapes 1-2-3

6 - Tester

7 - exposant e

8 - exposant d

9 - fichier

10 - FAQ

Cette activité est en réalité une activité de programmation qui permettra d'aborder la partie Mise au point des programmes et gestion des bugs : dans la pratique de la programmation, savoir répondre aux causes typiques de bugs :

expression booléenne mal exprimée justement (question 11),
effets de bord non désirés (voir l'activité Python - paradigmes de programmation),
débordements dans les tableaux (nous en avons longuement parlé en 1er),
instruction conditionnelle non exhaustive (question 13),
choix des inégalités (question 14),
mauvaise borne finale dans une boucle dont l'histoire du x-1 final si range(x) (question 23),
mauvaise initialisation d'une boucle non bornée (question 24),
comparaisons et calculs entre flottants,
problèmes liés au typage,
mauvais nommage des variables, etc.

Prérequis : -

Evaluation ✎ : questions -

Documents de cours : open document ou pdf

MODE COURS (cacher les questions)

1 - Principe du chiffrement asymétrique

⇩ ⇧ ⤊

Il y a eu plusieurs types de systèmes de chiffrement asymétrique. Nous ne verrons que la version qui correspond à la version actuelle de ce type de système : le système RSA.

Il comporte un clé Publique et une clé Privée dont voici le principe.

La clé Publique ne permet pas de décrypter les messages cryptés avec la clé Publique.

La clé Privée ne permet pas de décrypter les messages cryptés avec la clé Privée.

On peut décrypter avec la clé Privée les messages cryptés à l'aide de la clé Publique.

On peut décrypter avec la clé Publique les messages cryptés à l'aide de la clé Privée.

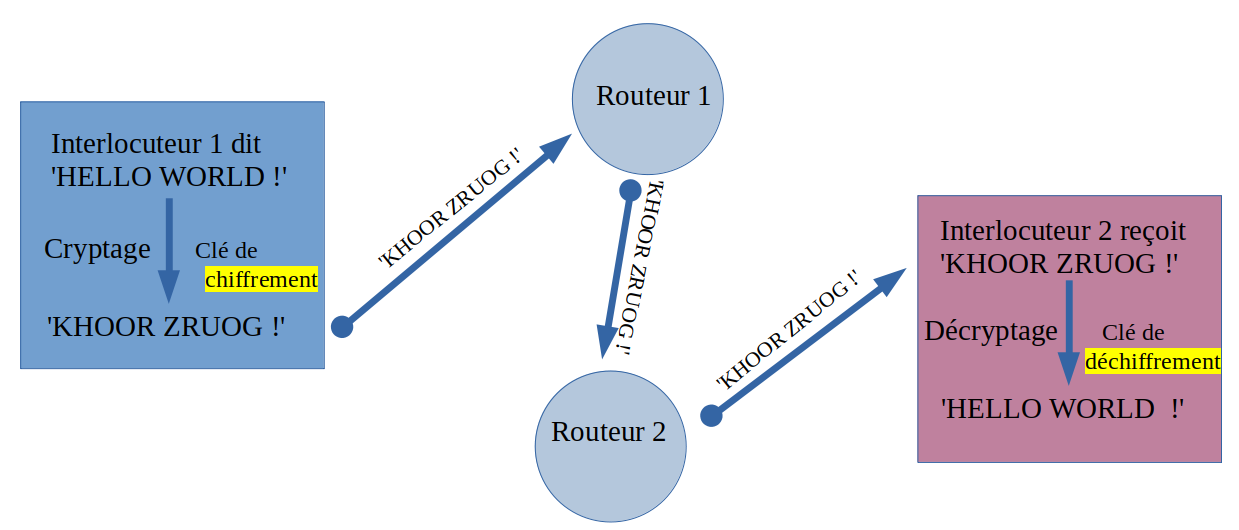
L'une des conditions de l'utilisation d'un tel chiffrement : qu'on ne puisse pas retrouver la valeur de la clé privée connaissant la valeur de la clé privée ou d'un message crypté quelconque. Il faut que cela soit trop compliqué et demande trop de temps ou qu'il existe beaucoup de valeurs possibles par exemple.

RSA est basé sur le principe des fonctions à sens unique : connaissant le message m, il est facile de chiffrer le message en calculant f(m) mais connaissant f(m) il est "difficile" de retrouver m. La notion de complexité algorithmique donne un moyen de quantifier la notion sinon floue de "difficile".

En outre, RSA utilise des fonctions à sens unique possèdant une brêche : connaissant la clé de déchiffrement, il devient "facile" de retrouver m connaissant f(m).

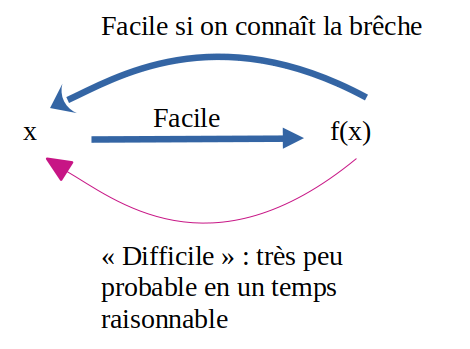
Là où c'est compliqué à mettre en place, c'est que trouver la brêche doit s'avérer "impossible" en un temps raisonnable.

2 - RSA

⇩ ⇧ ⤊

Le chiffrement RSA date de 1977 et doit son nom aux initiales de ses trois inventeurs :

Ronald Rivest (né en 1947, cryptologue américain)
Adi Shamir (né en 1962, mathématicien et cryptologue israélien)
Leonard Adleman (né en 1945, chercheur américain en informatique théorique, et en informatique-biologie moléculaire)

Rivest (par Ronald L. Rivest, CC BY-SA 4.0 , via Wikimedia Commons) - Shamir (par Erik Tews, CC BY-SA 3.0 , via Wikimedia Commons) - Adleman (par len adlmen, CC BY-SA 3.0 , via Wikimedia Commons)

RSA a été breveté par le MIT (Massachusetts Institute of Technology) en 1983 aux États-Unis.

Le brevet a expiré le 21 septembre 2000.

Le chiffrement RSA utilise de grands nombres premiers et le petit théorème de Fermat (lié à la division entière et à la congruence).

La facilité du chifrement et la difficulté du décryptage sont liées au fait qu'il est facile de calculer le produit n = p*q de deux nombres premiers p et q mais qu'il est difficile de retrouver p et q si on ne connaît que n.

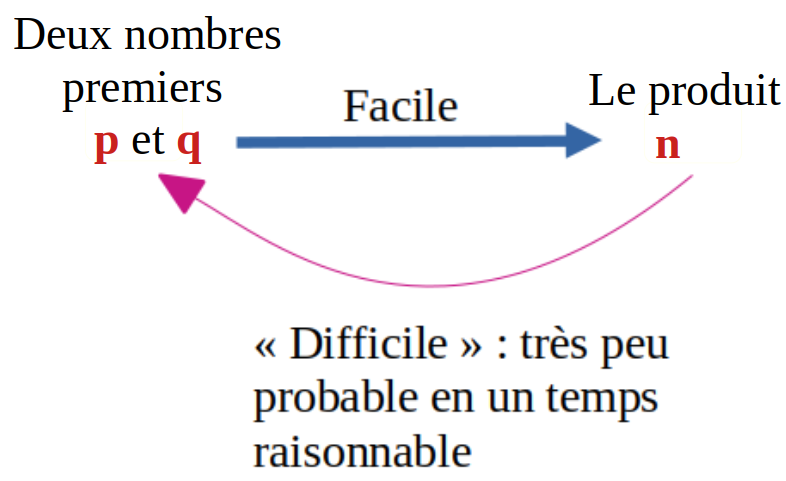
Vous allez donc comprendre l'intérêt qu'on porte aux nombres premiers et aux diviseurs communs.

Division entière ou euclidienne

Nous avons déjà vu la division euclidienne et la notion de reste.

Si a = b*q + r alors

La division euclidienne de a par b donne q : a // b = q .
Le reste de cette division entière est alors r : a % b = r avec r dans [0;b[ .

Exemple

Si on prend 15, on peut écrire que 15 = 2*6 + 3 .

La division euclidienne de 15 par 6 donne 2 : 15 // 6 = 2 .

Le reste de cette division est de 3 : 15 % 6 = 3 .

Congruence (hors programme)

La notion de congruence (hors programme en NSI, on ne l'aborde ici qu'en terme de culture générale) est liée à ce reste.

Exemples sans définition exacte

0, 6, 12, 18, 24, 30... sont congrus modulo 6 entre eux car le reste de leur division euclidienne par 6 donne un reste de 0 à chaque fois.

1, 7, 13, 19, 25, 31... sont congrus modulo 6 entre eux car le reste de leur division euclidienne par 6 donne un reste de 1 à chaque fois.

2, 8, 14, 20, 26, 32... sont congrus modulo 6 entre eux car le reste de leur division euclidienne par 6 donne un reste de 2 à chaque fois.

ect ...

Définition

Soient

n un entier naturel non nul et,
a et b deux entiers relatifs.

On dit que a et b sont congrus modulo n s'ils ont le même reste dans une division euclidienne par n.

En Python, on peut donc écrire a % n == b % n .

On dit aussi que a est congru à b modulo n .

Notation mathématique

La notation mathématique est a ≡ b (mod n) pour signaler que a et b sont congrus modulo n .

Exemple

156 = 17*9 + 3 . Donc 156 % 17 donne un reste de 3 .
105 = 17*6 + 3 . Donc 105 % 17 donne un reste de 3 .
On peut donc écrire que 156 ≡ 105 (mod 17) pour dire que 156 est congru à 105 modulo 17.

Conséquence

On remarquera que a ≡ b (mod n) implique que (a-b) est divisible par n :

En Python : (a-b) % n == 0

Ou encore : (a-b) // n == k avec k entier.

156 ≡ 105 (mod 17) implique que (156-105) / 17 donne un résultat entier.

En Python : (156-105) / 17 = 51 / 17 = 3.0

Exemple d'utilisation

La Clé Publique est un n-uplet cpub = (n, e) contenant deux informations notées n et e.

Sur notre exemple, nous prendrons cpub = (2159, 437)

Si m est un bout du message à chiffrer, on obtient le message chiffré mc correspondant en utilisant cette formule :

mc = (m^e) % n

n se nomme le module de chiffrement car il sert à faire un modulo et
e est l'exposant de chiffrement car on l'utilise en tant que mise à la puissance du message.

En Python, ça donnera :

mc = (m**e) % n

La Clé Privée est un n-uplet cpri = (n, d) contenant

le module de chiffrement n et
l'exposant de déchiffrement d.

Si mc est un bout du message chiffré, on obtient le message déchiffré md correspondant en utilisant cette formule :

md = (mc^d) % n

Bien entendu, si les valeurs sont correctes, on aura md = m !

Pour notre exemple, nous prendrons (pas par hasard !) cpri = (2159, 1181) .

On la gardera secrète de façon à être le seul à pouvoir déchiffrer les messages chiffrés avec la Clé Publique.

01° On désire transmettre par exemple 500 et 1000 de façon cryptée. Calculer les deux messages mc à envoyer après application basique du chiffrement sur 500 et 1000 avec cpub = (2159, 437) .

mc = (m**e) % n

Correction ?

...CORRECTION...

On n'envoie pas 500 mais (500**437) % 2159 ce qui donne 504.

On n'envoie pas 1000 mais (500**437) % 2159 ce qui donne 1746.

Le message envoyé est donc 504 suivi de 1746.

02° Que va donner le chiffrement d'un message valant 6000 ?

Correction ?

...CORRECTION...

En théorie, on calcule (6000**437) % 2159 ce qui donne 900.

03° La personne ayant émis la clé publique reçoit le message suivant : 504 - 1746 - 900. Sa clé privée (tenue secrète) est cpri = (2159, 1181) .

Comment retrouver le message déchiffré ?

Correction ?

...CORRECTION...

Il suffit d'appliquer ceci :

md = (mc^d) % n

On calcule (504**1181) % 2159 ce qui donne 500. Ca fonctione !

On calcule (1746**1181) % 2159 ce qui donne 1000. Ca fonctionne !

On calcule (900**1181) % 2159 ce qui donne 1682. Ca ne fonctione pas, le message de base était 6000 !

Limitation du message chiffré par rapport au module de chiffrement n

La valeur de n permet d'obtenir la plage des valeurs qui seront déchiffrables : les valeurs m à chiffrer doivent impérativement être dans l'intervalle [0, n[ ou [0, n-1], sinon on ne peut parviendra pas à déchiffrer correctement la valeur initiale.

Ici puisque n = 2159, cela veut dire qu'on ne peut chiffrer que des valeurs comprises entre 0 et 2158.

Attention, certaines valeurs ont un chiffrement assez problématique :

Les deux premières valeurs (0 et 1) et la dernière valeur (2158) posent problème :


>>> (0**437) % 2159
0        Un peu inutile car on retrouve le message de base...
 
>>> (2159**437) % 2159
0        Inutile car on obtiendra 0 en déchiffrant !


>>> (1**437) % 2159
1        Pas vraiment un chiffrement...
 
>>> (2158**437) % 2159
2158        Pas vraiment un chiffrement...

Entre 2 et 2157, ça fonctionne correctement :


>>> (2**437) % 2159
389
 
>>> (2157**437) % 2159
1770

Principe d'un vrai chiffrement

Le vrai chiffrement se fait sur un bloc d'octets en réalité sinon, on transforme simplement une valeur comprise entre 0 et 255. C'est problématique dans le cas d'un texte car il suffit alors de connaître la fréquence du "e" dans la langue utilisée, et on pourrait retrouver assez facilement la valeur chiffrée du "e".

On considère donc plutôt un encodage basé sur un ensemble d'octets et pas un octet unique.

On pourrait par exemple vouloir transmettre le string "AB" qui va se retrouver encodé en deux octets YZ: Y = 65 suivi de Z = 66 en ASCII.

On va alors considérer que le message m à envoyer est 65*256 + 66, soit 16706.

Dans ce cas, il faut donc que n soit supérieur à 255*256 + 255, 65535. Il faut donc un module de chiffrement n au moins égal à 65536...

C'est logique, 2 octets correspondent à 16 bits, 2¹⁶ possibilités, donc 2¹⁶ - 1 pour la valeur maximale en entier naturel.

Puisque n = p * q, les nombres premiers p et q ne doivent donc pas être trop petits à cause de cela également.

Une autre technique courante consiste à utiliser des permutations d'octets par exemple. Mais le but ici n'est pas de faire un exposé sur les implémentations réelles de RSA.

04° Quelle doit être la valeur minimale du module de chiffrement si on veut envoyer des blocs chiffrés de 4 octets ?

Correction ?

...CORRECTION...

On aura 4 octets W-X-Y-Z pesant respectivement 2²⁴, 2¹⁶, 2⁸ et 1.

Soit on calcule 255*2²⁴ + 255*2¹⁶ + 255*2⁸ + 255

Soit on voit que 4 octets correspondent à 32 bits, et on calcule 2³² - 1

Dans les deux cas, on obtient : 4 294 967 295.

La valeur de n devra donc être au moins de 4 294 967 296.

05° Peut-on utiliser des blocs de deux octets avec nos clés cpub = (2159, 437) et cpri = (2159, 1181) ?

Correction ?

...CORRECTION...

Non car le module de chiffrement n ne vaut que 2159, et donc moins que la valeur 65536 nécessaire pour deux octets.

06° Envoyer le message "Bonjour à tous" en utilisant simplement UNICODE : on chiffre chaque caractère directement par sa valeur unicode.

On utilisera les clés fournies dans cette activité.

On peut trouver les valeurs unicode des caractères en utilisant la fonction native de Python ord :


>>> ord('A')
65
 
>>> chr(65)
'A'

Attention à l'espace, qui est bien un caractère en lui-même.

Créer une fonction Python pour trouver la valeur UNICODE et une fonction Python pour renvoyer la valeur chiffrée pourrait vous simplifier la vie...

Correction ?

...CORRECTION...

A vous de travailler un peu !

3 - Détermination des clés RSA

⇩ ⇧ ⤊

Le principe de l'utilisation étant posé, regardons comment déterminer les clés.

Etape 1 : choisir deux nombres entiers p et q

Assez facile.

Pour notre exemple, nous prendrons par exemple p = 17 et q = 127 .

Attention, pour obtenir des clés réellement utilisables, il faut prendre de très grands nombres premiers !

Etape 2 : calculer le module de chiffrement n

Facile, c'est une multiplication.

n = p * q

Cette valeur sera transmise à la fois dans la clé publique et la clé privée.

La valeur de n n'est donc pas d'une donnée secrète. Par contre, les valeurs de p et q devront être dissimulées.

Avec nos valeurs de test, on obtient n = 17 * 127 , soit n = 2159 .

Ce nombre n'est pas un nombre premier, puisqu'il est décomposable.

Néanmoins, c'est bien de là que vient la "difficulté" du retour en arrière : si on vous donne un n très grand, on ne pourra pas retrouver p et q en un temps raisonnable.

Avec n = 2159 , ce n'est pas très difficile ok.

Avec n = 35823194494940926873 , c'est déjà plus diffile, non ?

Et encore, ce nombre n'est pas si grand que cela puisqu'il ne nécessite que 65 bits pour être encodé :


>>> n = p*q
>>> n
35823194494940926873
 
>>> bin(n)[2:]
'11111000100100101100011011001011111111110101011101101001110011001'
 
>>> len(_)
65
 
>>> p
3875804809
 
>>> q
9242775697

Si on prend un nombre n beaucoup plus grand, cela va forcément être encore plus difficile.

Taille de la clé asymétrique

Actuellement (2021), on considère que les clés asymétriques basées sur un nombre n de 2048 bits sont valables en terme de sécurité jusqu'en 2030. Au delà, on conseille d'augmenter le nombre de bits car la puissance de calculs aura bien évolué. Est-ce à dire que les clés asymétriques de 1024 bits ne sont plus sécurisées ? Tout dépends de ce que voulez protéger. Augmenter le nombre de bits, augmente en effet le temps d'exécution du chiffrement/déchiffrement.

En effet, contrairement au cas symétrique (où avec 128 bits, on a vraiment presque 2¹²⁸ valeurs possibles), une clé asymétrique de 128 bits ne présente qu'une seule factorisation possible. Cela restreint fortement le nombre de possibilités à tester. Il faut donc augmenter la taille de la clé.

Comment obtenir un nombre n sur 2048 bits

Le plus simple est d'avoir deux nombres premiers p et q de 1024 bits chacun.

Etape 3 : calculer indicatrice d'Euler φ

Etape facile, c'est un simple calcul.

φ = (p-1) * (q-1)

Ici, on obtient φ = (17-1) * (127-1) , soit φ = 2016 .

Etape 4 : choisir l'exposant de chiffrement e

Cette étape est plus délicate à réaliser. Nous allons voir qu'il va falloir utiliser l'algorithme d'Euclide.

Sans un bon algorithme, cette simple recherche peut prendre du temps.

Ce exposant de chiffrement e doit être

un entier inférieur à φ
premier avec φ : e ne doit pas partager de diviseur commun avec φ , d'où l'algorithme d'Euclide.

Ici, on a φ = 2016 et on ne pourrait pas prendre e = 2014 car 2016 et 2014 sont divisibles par 2.

On peut décomposer 2016 de cette façon : 2016 = 2⁵ * 3² * 7 : 2, 3 et 7 sont donc les diviseurs à ne pas prendre pour e.

Il suffit donc de prendre un nombre e qui ne soit divisible ni par 2, ni par 3, ni par 7.

Prenons par exemple e = 19 * 23 , soit e = 437 .

Il existe donc de nombreuses valeurs admissibles de e. Ces valeurs dépendent de φ et donc uniquement indirectement de p et q. Le principe est de ne pas permettre à quelqu'un connaissant la clé publique (donc e) d'obtenir d'indice supplémentaire sur les valeurs possibles de p et q.

Etape 5 : trouver l'exposant de déchiffrement d (connaissant e et φ)

Ce exposant de déchiffrement d doit être l'inverse de e modulo φ.

Cela veut dire qu'il faut respecter cette condition : le reste de la division entière de (e*d) par φ vaut 1.

(e * d) % φ = 1

D'où la notion d'inverse "e = 1 / d".

Dans le cas de notre exemple :

Indicatrice d'Euler φ = 2016
Exposant de chiffrement e = 437
on détermine que l'exposant de déchiffrement est d = 1181

Vérification avec Python :


>>> e = 437
>>> d = 1181
>>> phi = 2016
>>> (e*d) % phi
1

Cette fois, il faudra utiliser l'algorithme d'Euclide étendu. Sinon, encore une fois, cela prendrait un temps énorme pour p et q de grande taille.

Trouver d ?

Pour déterminer d, il faut connaître e (facile, c'est dans la clé publique) et φ (non connue car cette valeur n'est pas publiée). Or pour connaître φ, il faut parvenir à retrouver p et q à partir de n ! C'est donc difficile algorithmiquement.

On vient donc bien de dire que connaître la clé publique (n ,e) ne permet pas de trouver facilement la clé privée ou secrète (n, d).

4 - TP Python - Vérifier la primalité d'un entier

⇩ ⇧ ⤊

Le but de cette activité est d'automatiser tout cela pour générer une clé privée et une clé publique automatiquement.

Il ne s'agit pas de réaliser une véritable implémentation de RSA permettant de générer une clé de 2048 bits ! Juste de manipuler un peu le système pour voir qu'il fonctionne et que manipuler des grands nombres nécessite de faire attention à nos algorithmes, sinon c'est looooooooooong.

07° Installer matplotlib.

Nous allons devoir trouver deux nombres premiers.

Il va donc falloir vérifier qu'un entier donné est un nombre premier ou pas. Une tâche pas trop compliqué si ce nombre est petit mais un calcul qui devient de plus en plus long lorsque le nombre devient important.

Nombre premier

Définition : un nombre premier est un nombre entier naturel qui n'est divisible que par 1 et par lui-même.

Exemples :

5 est premier car il n'est divisible que par 1 et 5.
6 n'est pas premier car il est divisible par 1, 2, 3 et 6.
7 est premier car il n'est divisible que par 1 et 7.
8 n'est pas premier car il est divisible par 1, 2, 4 et 8.

Les nombres premiers inferieurs à 100 sont : 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61,67,71, 73, 79, 83, 89 et 97.

Jusque là, tout va bien.

Mais comment faire pour un nombre de grande taille, disons 170141183460469231731687303715884105727 ?

Une version naïve d'une fonction vérifiant si un nombre est premier est donc de vérifier qu'il ne soit pas divisible par l'un des entiers qui lui sont strictement inférieurs (à part 1).

Algorithme le plus brute et naïf qui soit

On tente de diviser x un par un par tous les nombres entiers dans [2;x[.

La version avec un while :

def est_premier_v1(x):
    """Fonction très naïve qui recherche si un nombre est premier par force brute"""
    assert type(x) == int
    d = 2
    while x % d != 0:  # tant que d n'est pas un diviseur de x
        d = d + 1
    if d < x:  # on a rencontré un diviseur avant d'atteindre x
        reponse = False
    else:
        reponse = True
    return reponse

La version avec un for :

def est_premier_v1(x):
    """Fonction très naïve qui recherche si un nombre est premier par force brute"""
    assert type(x) == int
    for d in range(2, x, 1):
        if x % d == 0:  # si d est un diviseur de x
            return False  # On vient de rencontrer un diviseur
    return True  # Nous n'avons pas rencontré de diviseur

Prenons le cas de 18. On voit bien que pour tester la primalité, il suffira de le diviser par deux et c'est plié : le reste est nul.

08° Première question : un nombre (et donc pair) peut-il être divisible par 4, 8, 16... sans être divisible par 2 ?

Deuxième question : une fois qu'on a vérifié la division par 2, quels sont les prochains diviseurs à tester ?

Correction ?

...CORRECTION...

Non, il ne sert à rien de vérifier les diviseurs pairs à part 2 : si un nombre est pair, il sera divisible par 2. A part s'il s'agit de x = 2 justement, x n'est donc pas un nombre premier.

Il suffit donc de tester 2 puis 3, 5, 7... : les nombres impairs.

09° Version avec un peu d'algorithmique : modifier la fonction (version avec while) de façon à ce qu'elle renvoie bien la bonne réponse mais en utilisant le petit truc de la parité :

Si x est égal à 2 : on renvoie True.
Sinon si x est pair : on renvoie False.
Sinon : on effectue la boucle TANT QUE mais cette fois, on commence à 3 et on augmente de 2 pour ne prendre que les nombres impairs.

Correction ?

...CORRECTION...

def est_premier_v1(x):
    """Fonction naïve qui recherche si un nombre est premier par force brute (version sans la racine)"""
    assert type(x) == int
    if x == 2:  # si x vaut 2, on renvoie True
        reponse = True
    elif x % 2 == 0:  # sinon si x est pair, on renvoie False
        reponse = False
    else:  # sinon, il faut chercher
        d = 3
        while x % d != 0:  # tant que d n'est pas un diviseur de x
            d = d + 2
        if d < x:  # on est sorti avant d'avoir atteint x
            reponse = False
        else:
            reponse = True
    return reponse

Prenons le cas de 100. Voici les différentes façons de décomposer 100 (qui n'est pas premier)

100 = 1 * 100
100 = 2 * 50
100 = 4 * 25
100 = 5 * 20
100 = 10 * 10.

Au delà de la racine de 100, 10, on va donc retrouver les mêmes valeurs mais en inversant leur ordre :

100 = 20 *5
100 = 25 * 4
100 = 50 * 2
100 = 100 * 1

Prenons le cas de 103. Sa racine vaut approximativement 10.14889156509222. Pour savoir s'il est premier, il est inutile de chercher un diviseur éventuel supérieur à 10 :

soit on trouve un diviseur inférieur à 10 et on saura que 103 n'est pas premier.

103 % 2 = 1 car 103 = 2 * 51 + 1
103 % 3 = 1 car 103 = 3 * 34 + 1
103 % 5 = 3 car 103 = 5 * 20 + 3
103 % 7 = 5 car 103 = 7 * 14 + 5
103 % 9 = 4 car 103 = 9 * 11 + 4

il est inutile de continuer : il faudrait écrire 11 * quelque chose de supérieur à 10 sinon nous l'aurions trouvé avant ! Or, même 10*11 donne 110 donc quelque chose de supérieur à 103...

Trouver un diviseur avec la racine

Pour un nombre x, s'il existe un diviseur supérieur à la racine de x, c'est qu'il existe nécessairement un diviseur inférieur à la racine de x.

x = a * b

S'il existe a plus grand que la racine de x, c'est que b est plus petit que la racine de x
S'il existe a plus petit que la racine de x, c'est que b est plus grand que la racine de x.

Moralité : si on cherche les diviseurs du plus grand ou plus petit, on finira pas tomber d'abord sur le plus petit : inutile de continuer après la racine si on n'a pas trouver avant la racine.

10° Considérons un nombre x et notons r sa racine carrée. Montrer par l'absurde qu'on ne peut pas écrire x = a * b avec a et b supérieurs à r.

Correction ?

...CORRECTION...

Supposons qu'on puisse écrire ceci :

x = a * b avec a = (r + u) et b = (r + v) où u et v sont des entiers supérieurs ou égaux à 0.

On part donc de ceci :

x = (r + u) * (r + v)

Si on distribue :

x = r² + r*(u+v) + u*v

Si r, u et v sont positifs, le terme de droite est donc supérieur à r²
Or, r est la racine de x : x = r²
On devrait alors écrire ceci :

r² = r² + r*(u+v) + u*v

Cela revient à écrire qu'un nombre est inférieur à lui-même ou que deux nombres différents sont égaux !

Ce résultat est clairement faux (ou absurbe). C'est donc que l'hypothèse de base est fausse.

On ne peut donc pas écrire que x soit le produit de deux nombres supérieurs à la racine de x.

11 - Programmation et bugs° Quelqu'un veut créer un programme en utilisant cette notion de a et b supérieurs à r. Voici l'un de ses tests. Que teste-on réellement ici ?

`1`	`if a and b > r:`

Que faut-il écrire pour réellement tester a et b supérieurs à r ?

Correction ?

...CORRECTION...

Python lit ceci : (a) et (b supérieurs à r).

On teste si a est non nul (ou non vide, non ""...) et si b est lui supérieur à r. Le and est prioritaire.

Rappel : a and b peut s'écrire a.b dans l'algèbre de Bool.

Il faudrait écrire :

`1`	`if a > r and b > r:`

Attention : c'est une source assez courante d'erreurs dans les programmes produits par les élèves et les étudiants.

12° Utiliser cette (mauvaise) version du prédicat est_premier_v1(x) pour vérifier qu'il renvoie bien True si x est premier et False sinon.

Cette fonction va au delà de la racine et est donc assez mal conçue.

def est_premier_v1(x):
    """Fonction naïve qui recherche si un nombre est premier par force brute"""
    assert type(x) == int
    if x % 2 == 0:  # sinon si x est pair, on renvoie False
        reponse = False
    elif x == 2:  # si x vaut 2, on renvoie True
        reponse = True
    else:  # sinon, il faut chercher
        d = 3
        while x % d != 0:  # tant que d n'est pas un diviseur de x
            d = d + 2
        if d < x:  # on a rencontré un diviseur avant d'atteindre x
            reponse = False
        else:
            reponse = True
    return reponse

La fonction gère déjà le cas 2 ou pair. Le TANT QUE doit gérer le cas d'un diviseur supérieur ou égal à 3 puisqu'on commence à diviser x par 3. Il faut continuer à modifier d dans la boucle non bornée TANT QUE la division euclidienne de x par d ne donne par un reste nul et que d est inférieur à x.


>>> est_premier_v1(13)
True
 
>>> est_premier_v1(8191)
True
 
>>> est_premier_v1(131071)
True
 
>>> est_premier_v1(524287)
True
 
>>> est_premier_v1(1008001)
True
 
>>> est_premier_v1(10003199)
True
 
>>> est_premier_v1(100003679)
True

La fonction a l'air de fonctionner mais...

13 - Programmation et bugs° Pourquoi la fonction ne fonctionne-t-elle pas pour 2 alors qu'elle ne provoque pas d'erreur et qu'elle semble fonctionner pour les valeurs supérieures à deux ?

Modifier la fonction pour qu'elle fonctionne, même pour 2.


>>> est_premier_v1(2)
False

Correction ?

...CORRECTION...

L'interpréteur Python n'effectue que l'UN des blocs d'une instruction conditionnelle. Or, il teste les conditions dans l'ordre proposé.

Le problème vient ici de la mauvaise organisation du test : on teste si x est un multiple de 2 avant de tester s'il s'agit de 2.

En réalité, on ne poura jamais atteindre la ligne 7 ! Si on transmet l'argument 2, alors la condition est vraie en ligne 4 et donc on exécute le bloc constitué de la ligne 5, puis, on sort de l'instruction conditionnelle pour atteindre la ligne 16.

Attention : c'est une source assez courante d'erreurs dans les programmes produits par les élèves et les étudiants. Il convient de bien réflechir :

à l'ordre des conditions d'exécution : intervertir deux tests peut conduire à ne pas demander à l'interpréteur réellement ce qu'on désire. Dans certains cas comme ici, un test écrase un autre test : le cas multiple de deux écrase ici le cas deux tout court.

if a > 10:
    fait un truc
elif a > 20:
    fait un autre truc
else:
    fait le truc par défaut

Ici, on fera toujours le premier bloc même si on a 20, 21 ou 1089000. Pourquoi ? Tout simplement car tous ces nombres sont bien supérieurs à 10 !

à vérifier que tous les cas sont bien traités : parfois, on oublie toute une gamme de valeurs possibles et on se retrouve avoir une valeur vide ou une valeur par défaut qui ne correspond à rien.

if a > 0:
    fait un truc
elif a < 0:
    fait un autre truc

On remarque qu'ici, on ne fait donc rien pour a = 0 !

Dans notre cas, il faut donc intervertir les lignes 4-5 et 6-7.

def est_premier_v1(x):
    """Fonction naïve qui recherche si un nombre est premier par force brute"""
    assert type(x) == int
    if x == 2:  # si x vaut 2, on renvoie True
        reponse = True
    elif x % 2 == 0:  # sinon si x est pair, on renvoie False
        reponse = False
    else:  # sinon, il faut chercher
        d = 3
        while x % d != 0 :  # tant que d n'est pas un diviseur de x
            d = d + 2
        if d < x:  # on est sorti avant d'avoir atteint x
            reponse = False
        else:
            reponse = True
    return reponse

14 - Programmation et bugs° Aidez ce pauvre programmeur qui ne comprend pas pourquoi sa propre fonction ne fonctionne pas alors qu'il a bien fait ce qu'on lui demande : on divise par les entiers de 3 jusqu'à l'entier x dont on veut tester la primalité. Il a pourtant "presque" la même chose que nous... Et c'est ce "presque" qui pose problème.


>>> est_premier_v1(13)
False

Voici sa fonction :

def est_premier_v1(x):
    """Fonction naïve qui recherche si un nombre est premier par force brute"""
    assert type(x) == int
    if x == 2:  # si x vaut 2, on renvoie True
        reponse = True
    elif x % 2 == 0:  # sinon si x est pair, on renvoie False
        reponse = False
    else:  # sinon, il faut chercher
        d = 3
        while x % d != 0:  # tant que d n'est pas un diviseur de x
            d = d + 2
        if d <= x:  # on est sorti avant d'avoir atteint x
            reponse = False
        else:
            reponse = True
    return reponse

Correction ?

...CORRECTION...

Le problème vient de la ligne 12 : il a utilisé un ≤ et pas un <.

Il s'agit d'une cause courante de mauvais fonctionnement. Cela ne provoque pas d'erreurs détectables par l'interpréteur mais provoque juste une mauvaise réponse.

15° Mettre le code suivant en mémoire. Il comporte 5 fonctions :

le prédicat est_premier_v1(x) qui teste naïvement si x est premier en allant au delà de la racine
le prédicat est_premier_v2(x) qui teste naïvement si x est premier en allant uniquement jusqu'à racine de x.
la fonction duree_v1(x, nb_essais=10) qui renvoie un float correspondant au nombre de secondes pour que la fonction est_premier_v1 réponde, sur une moyenne de 10 essais par défaut.
la fonction duree_v2(x, nb_essais=10) fait la même chose mais pour est_premier_v2.
la fonction trace_duree(t, nb_essais=10) qui trace un graphique correspondant aux durées moyennes pour répondre à la primalité des entiers contenus dans le tableau t, entier par entier. Elle ne renvoie rien, c'est une fonction-procédure d'interface créant un simple affichage.

"""
Module maison de recherche de primalité pour RSA.
Ne propose que la version la plus naïve de trouver si un nombre est premier ou pas
Plus de performance ? Il faudra plus de maths :o)
"""
 
# Importations
 
import random
import math
import matplotlib.pyplot as plt
import timeit
 
# CONSTANTES : deux tableaux contenant quelques nombres premiers
 
NBP = [3, 7, 13, 29, 47, 127, 179, 257, 521, 1039, 2111]
NBP2 = [3, 7, 13, 29, 47, 127, 179, 257, 521, 1039, 2111, 8191, 131071, 524287, 1008001]
 
# Fonctions pour l'étape 1
 
def est_premier_v1(x):
    """Fonction naïve qui recherche si un nombre est premier par force brute (version sans la racine)"""
    assert type(x) == int
    if x == 2:  # si x vaut 2, on renvoie True
        reponse = True
    elif x % 2 == 0:  # sinon si x est pair, on renvoie False
        reponse = False
    else:  # sinon, il faut chercher
        d = 3
        while x % d != 0:  # tant que d n'est pas un diviseur de x
            d = d + 2
        if d < x:  # on est sorti avant d'avoir atteint x
            reponse = False
        else:
            reponse = True
    return reponse
 
def est_premier_v2(x):
    """Fonction naïve qui recherche si un nombre est premier par force brute (version avec la racine)"""
    assert type(x) == int
    if x == 2:  # si x vaut 2, on renvoie True
        reponse = True
    elif x % 2 == 0:  # sinon si x est pair, on renvoie False
        reponse = False
    else:  # sinon, il faut chercher
        d = 3
        r = math.floor(math.sqrt(x))
        while x % d != 0 and d <= r:
            d = d + 2
        if d <= r:  # il y a bien un diviseur avant x
            reponse = False
        else:
            reponse = True
    return reponse
 
def duree_v1(x, nb_essais=10):
    """Renvoie la durée pour déterminer avec est_premiers_v1 si x est premier ou pas"""
    duree_totale = timeit.timeit(
        f"est_premier_v1({x})",
        setup="from __main__ import est_premier_v1",
        number = nb_essais)
    return duree_totale / nb_essais
 
def duree_v2(x, nb_essais=10):
    """Renvoie la durée pour détermineravec est_premiers_v2 si x est premier ou pas"""
    duree_totale = timeit.timeit(
        f"est_premier_v2({x})",
        setup="from __main__ import est_premier_v2",
        number = nb_essais)
    return duree_totale / nb_essais
 
def trace_duree(t, f, nb_essais=10):
    """Trace la courbe moyenne du temps de recherche de primalité avec la fonction f des entiers dans t"""
 
    # Création de durées par extentsion et ajouts successifs pour voir le déroulement
    durees = []
    for n in t:
        print(f"Travail en cours avec {n}")
        durees.append(f(n, nb_essais))
    print("Terminé")
 
    # Création de nb_bits par compréhension
    nb_bits = [math.floor(math.log2(n)) + 1 for n in t]
    # ou nb_bits = [len(bin(n)[2:]) for n in t]
 
    # Choix des axes
    axe_x = nb_bits  # Abscisse
    axe_y = durees  # Ordonnée  
    x_max = max(axe_x)
    y_max = max(axe_y)
 
    # Création du graphique
    plt.plot(axe_x, axe_y, label="Temps de recherche 1er essai", color="red")
    # plt.plot(axe_x, [2**(b/2)/((2**(axe_x[-1]/2))/axe_y[-1]) for b in axe_x], color='blue', label="Temps de recherche théorique")
    plt.xlabel("Bits d'encodage")
    plt.ylabel("Temps d'exécution moyen(s)")
    plt.title("Comparaison des temps d'exécution")
    plt.legend(loc='upper left')
    plt.axis([0, x_max, 0, y_max])
    plt.grid()
    plt.show() # Affichage à l'écran des courbes

16° Tester la rapidité des deux fonctions en utilisant les nombres premiers stockés dans NBP, le tableau de NomBres Premiers.

`16`	`NBP = [3, 7, 13, 29, 47, 127, 179, 257, 521, 1039, 2111]`


>>> duree_v1(NBP[0])
1.8533000911702402e-06
 
>>> duree_v1(NBP[1])
3.363799987710081e-06
 
>>> duree_v1(NBP[2])
4.335299854574259e-06
 
>>> duree_v1(NBP[3])
6.7793998823617585e-06
 
>>> duree_v1(NBP[4])
1.0627700066834223e-05
 
>>> duree_v1(NBP[5])
1.2311300088185817e-05
 
>>> duree_v1(NBP[6])
1.2284100012038835e-05
 
>>> duree_v1(NBP[7])
4.099059988220688e-05
 
>>> duree_v1(NBP[8])
5.155100006959401e-05
 
>>> duree_v1(NBP[9])
0.00012017009994451655
 
>>> duree_v1(NBP[10])
0.000294514900087961

Question : que constate-t-on au niveau des temps de réponses lorsque le nombre premier devient de plus en plus grand ? A quoi est-ce dû ?

17° Comparer plusieurs durées d'exécution pour un même nombre premier en fournissant un seul essai à chaque fois. Pourquoi a-t-on de telles différentes ?


>>> duree_v1(2111, 1)
0.0002949560002889484
 
>>> duree_v1(2111, 1)
0.00023148800028138794
 
>>> duree_v1(2111, 1)
0.00027341500026523136
 
>>> duree_v1(2111, 1)
0.0007015280007180991

Correction ?

...CORRECTION...

La durée nécessaire pour répondre n'est pas une grandeur propre à notre fonction et à ses données d'entrée. Cette durée est fortement dépendante de l'occupation du microprocesseur par d'autres tâches.

18° Pour obtenir un temps d'exécution moyen, on peut donc demander à notre fonction d'évaluer cette durée non pas sur un seul essai mais sur plusieurs milliers par exemple.


>>> duree_v1(2111, 1000)
0.00017470132400012516
 
>>> duree_v1(2111, 1000)
0.0001734132050005428
 
>>> duree_v1(2111, 1000)
0.0001750983299989457
 
>>> duree_v1(2111, 1000)
0.00017563680700004625

Que vaut cette durée ici avec un seul nombre significatif ?

Correction ?

...CORRECTION...

En moyenne, on voit qu'on peut écrire :


0.0002

Le 2 est à la 4e position derrière la virgule. On peut don également écrire ceci :


2.10^-4


2E-4

19° Comparer les temps d'exécution pour notre deuxième fonction de recherche, celle qui ne cherche les diviseurs que jusqu'à la racine carré de x.


>>> duree_v2(2111, 1000)
4.331548000563634e-06

Exprimer les durées des questions 18 et 19 en puissance de 10^-6 puis comparer les durées moyennes d'exécution des questions 16 et 17.

Correction ?

...CORRECTION...

Ici la durée moyenne est de 4.10^-6.

Lors de la question précédente, nous avions 2.10^-4, soit 20.10^-5 ou encore 200.10^-6.

On compare les deux durées en calculant la plus grande sur la plus petite.

Cela revient à calculer 200/4, ce qui donne 50.

Pour le cas NBP[10] = 2111, la fonction gérant la recherche jusqu'à la racine carrée est donc 50 fois plus rapide que l'autre.

20° La durée est liée aux nombres de diviseurs à vérifier (nombre de fois où on effectue la boucle), à la taille (en octets) du nombre x par rapport aux nombres d'octets ainsi qu'à la taille (en octets) du diviseur...


>>> duree_v2(1008001, 10000)
8.181419499996992e-05
 
>>> duree_v2(1008003, 10000)
1.609260599980189e-06
 
>>> duree_v2(1008005, 10000)
1.8608375999974668e-06
 
>>> duree_v2(1008002, 10000)
6.398853001883253e-07

Questions

Pourquoi les temps de réponses pour 1008003, 1008005 et 108002 (ces 3 nombres ne sont pas premiers) sont-ils bien plus bas que pour le nombre premier 1008001 ?
Pourquoi la réponse pour 108002 est-elle encore plus rapide ?
Que devrait faire cette durée pour vérifier de vrais nombres premiers de plus en plus grands ?

Correction ?

...CORRECTION...

Pour les 3 nombres non premiers, la réponses est rapidement car on tombe rapidement sur un diviseur qui donne un reste nul.

Dans le cas du nombre pair, c'est encore plus rapide car on ne rentre même pas dans la boucle : on teste le fait que le nombre soit pair avec le IF de la ligne 43.

Plus le nombre va devenir grand, plus le temps de réponse va augmenter considérablement s'il s'agit bien d'un nombre premier.

21° Utiliser les appels suivants qui vont permettre de comparer les durées mais également les allures des coûts. Gagne-t-on simplement en temps en utilisant la limite de la racine carrée ?


>>> trace_duree(NBP, duree_v1, 1000)
 
>>> trace_duree(NBP, duree_v2, 100000)

Correction ?

...CORRECTION...

Version 1

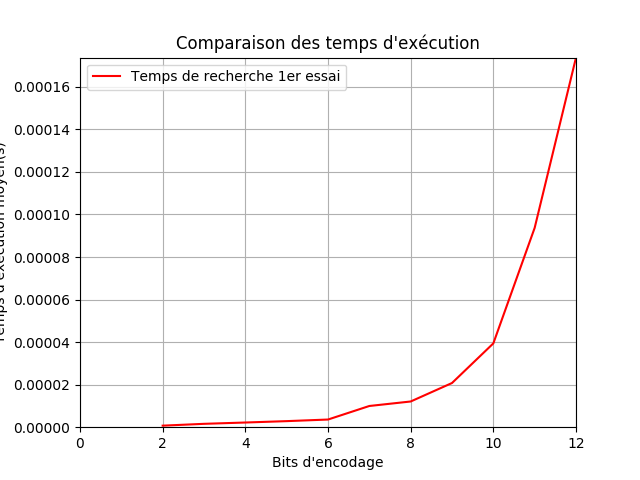
Version 2

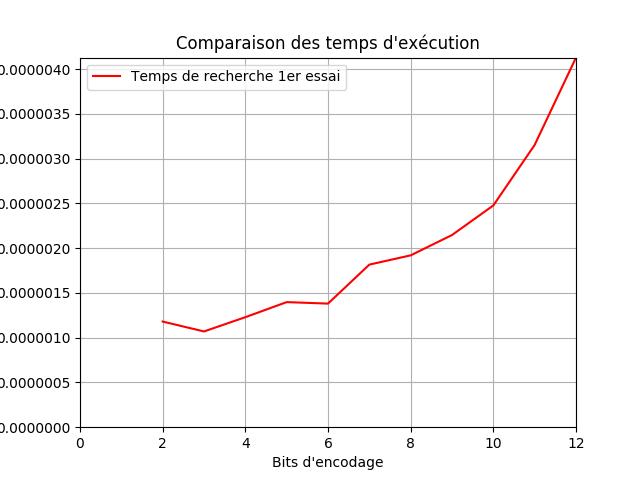
On voit donc clairement qu'en plus de la valeur brute de la durée, on gagne également sur l'allure du coût.

Complexité de l'algorithme naïf

Nous avons vu qu'avec un peu d'algorithmique (on teste uniquement les entiers impairs) et de mathématique (on teste uniquement les diviseurs jusq'à la racine carrée), on était parvenu à améliorer la rapidité de la réponse pour un entier premier.


>>> trace_duree(NBP2, duree_v2, 100000)

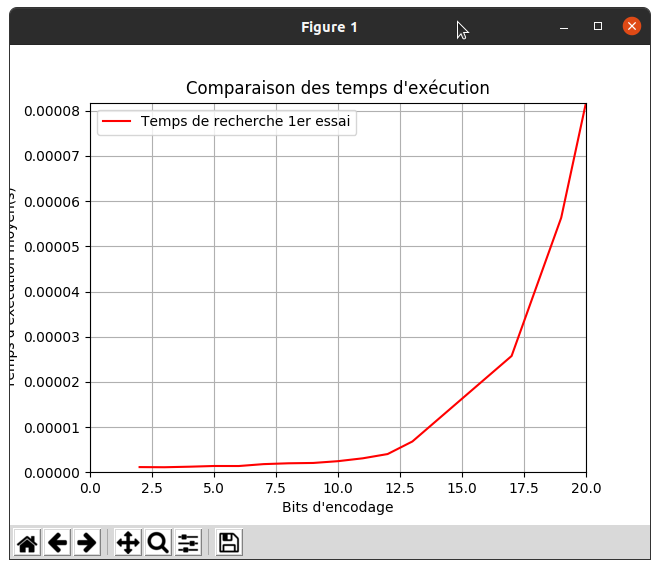
Réfléchissons un peu au coût d'une réponse sur un nombre premier x.

Avec 2 bits b, on peut écrire des nombres de 0 à 3.

Avec 3 bits b, on peut écrire des nombres de 0 à 7.

Avec 4 bits b, on peut écrire des nombres de 0 à 15.

Avec b bits, on peut écrire des nombres de 0 à 2^b-1.

Le lien entre n et b est donc de type 2^b.

Cela veut donc dire que le lien entre b et n est de type log2(n).

Si on en revient à notre algorithme :

Au pire, on doit faire autant de tours de boucle que la racine carrée de x. La complexité semble donc liée à ceci :

On pourrait croire que le coût de l'algorithme est lié à la racine carré mais en réalité la difficulté du travail demandé dépend du nombre de bits nécessaires à l'encodage du nombre.

Or, puisque la racine carré n'est rien d'autres que la mise à la puisance 1/2, on peut donc écrire que :

Le coût de la recherche de primalité d'un nombre quelconque s'exprimant avec b bits est en O(2^b/2)
Le coût de la recherche de primalité d'un nombre premier s'exprimant avec b bits est en Θ(2^b/2)

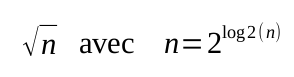
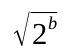
Conclusion : on ne pourra pas utiliser cet algorithme pour créer des nombres premiers de 512 bits au moins.

Déçu ? Eh oui. Il va falloir cette fois abandonner les méthodes de résolution purement informatique et sortir l'arsenal des mathématiques. Mais ce n'est pas pour tout de suite, ni pour cette année. Nous allons donc nous limiter à des recherches sur des nombres premiers d'une vingtaine de bits chacune. C'est déjà pas mal. Ca permettra de créer des clés de 40 bits.

En prenant quelques minutes, on pourrait rajouter quelques bits supplémentaires mais rien qui permettent de vraiment d'atteindre 1024 bits ou plus. Pour cela, il va falloir gagner quelques niveaux en mathématiques d'abord.

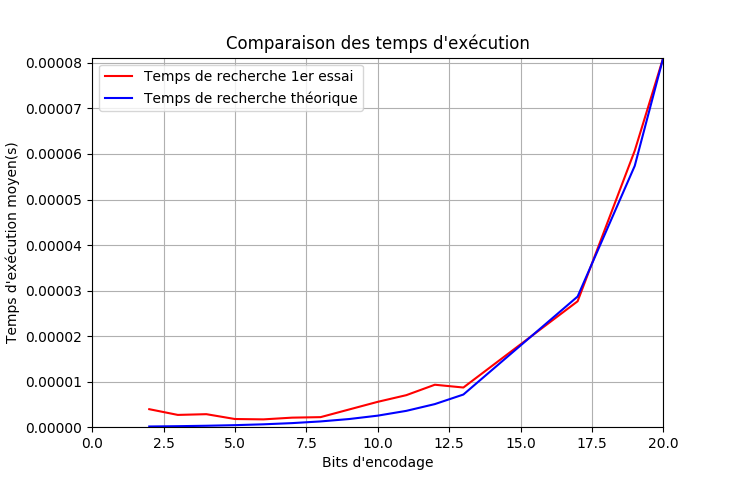
22° Décommenter la ligne 94. Vous allez pouvoir obtenir la comparaison entre la courbe réelle des durées d'exécution et la courbe théorique exponentielle.

1
2
3

# Création du graphique
plt.plot(axe_x, axe_y, label="Temps de recherche 1er essai", color="red")
plt.plot(axe_x, [2**(b/2)/((2**(axe_x[-1]/2))/axe_y[-1]) for b in axe_x], color="blue", label="Temps de recherche théorique")

Pour finir avec cette partie, voici l'allure des durées de traitement pour déterminer la primalité des entiers jusqu'à 1 million (à peine 20 bits donc)

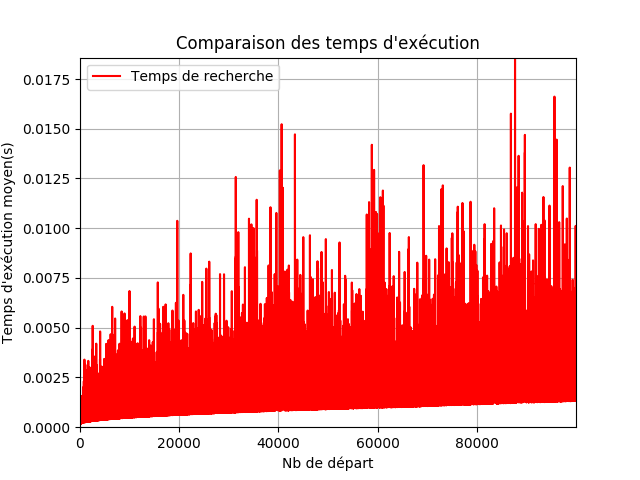
On peut voir que la durée évolue à peine dans le cas d'un nombre non-premier (le bas de la courbe) mais qu'il devient de plus en plus long d'estimer si un grand nombre premier est premier.

23 - programmation et bugs° Dernière chose : quelqu'un propose une dernière implémentation de la fonction. Plutôt que d'utiliser un while pour implémenter le TANT QUE, il est passé par un for associé au fait qu'on sorte de la fonction après avoir rencontré un return.

Questions :

qu'est-ce qui provoque l'exécution des exemples du docstring (qui normalement ne sont que des exemples présents dans la documentation ?
Pourquoi les exemples ne font-ils pas se lancer automatiquement si on importe le module et qu'on le lance depuis un autre script ?
Pourrait-on la ligne vide 21 ?
où se trouve l'erreur ? Modifier le code pour qu'elle fonctionne.

def est_premier_v3(x:int) -> bool:
    """Fonction naïve qui recherche si un nombre est premier par force brute
 
    :: param x(int)   :: un entier positif
    :: return (bool)  :: True si x est premier, False sinon
    .. ATTENTION : cette version disfonctionne si elle n'est pas modifée
 
    :: exemples ::
    >>> est_premier_v3(7)
    True
    >>> est_premier_v3(5)
    True
    >>> est_premier_v3(25)
    False
    >>> est_premier_v3(4)
    False
    >>> est_premier_v3(11)
    True
    >>> est_premier_v3(15)
    False
 
    """
 
    if x == 2:
        return True
    elif x % 2 == 0:
        return False
    else:
        limite = math.floor(math.sqrt(x))
        for d in range(3, limite, 2):
            if x % d == 0 :
                return False
    return True
 
if __name__ == '__main__':
    import doctest
    doctest.testmod()


**********************************************************************
File "activite_prog_rsa.py", line 31, in __main__.est_premier_v3
Failed example:
    est_premier_v3(25)
Expected:
    False
Got:
    True
**********************************************************************
File "activite_prog_rsa.py", line 37, in __main__.est_premier_v3
Failed example:
    est_premier_v3(15)
Expected:
    False
Got:
    True
**********************************************************************
1 items had failures:
   2 of   6 in __main__.est_premier_v3
***Test Failed*** 2 failures.

Correction ?

...CORRECTION...

Révision "Python - Documenter et Tester" : C'est la fonction testmod du module doctest qui va lire les docstrings des fonctions et va comparer les résultats obtenus avec ceux indiqués dans les exemples.
Révision "Python - Création de module" : Tel que l'appel à cette fonction est faite (ligne 35), on voit qu'elle ne sera activée que si on lance directement le script : le nom interne du module doit bien être MAIN, comme module principal. La fonction ne serait pas lancé si on importe ce module dans un autre script.
Révision "Python - Documenter et Tester" : ce n'est pas une erreur. Si on ne laisse pas de vide, la fonction va croire que le dernier appel doit renvoyer ceci :


    False
    '''

L'erreur vient encore une fois d'une erreur assez courante avec Python : la mauvaise valeur finale dans la boucle puisqu'on n'atteint pas la valeur mais on s'arrête juste avant.

29
30

        limite = math.floor(math.sqrt(x))
        for d in range(3, limite, 2):

Ici, on récupère donc l'arrondi inférieur de la racine (floor comme plancher).

Or dans la boucle, on mentionne cette valeur : on s'arrête donc 1 avant !

Avec 25, on obtient 5.0 arrondi à 5 ok. Mais dans la boucle, on ira que jusqu'à ... 4. Et donc, la fonction renvoie que c'est un nomvre premier. Et ça fonctionne mal avec tous ! 9 donne 3 et donc on s'arrête au diviseur 2. 100 donne 10 et on s'arrête à 9.

Comment corriger ? En rajoutant 1, soit à la limite, soit dans la boucle.

29
30

        limite = math.floor(math.sqrt(x))
        for d in range(3, limite + 1, 2):

29
30

        limite = math.floor(math.sqrt(x)) + 1
        for d in range(3, limite, 2):

5 - Etapes 1-2-3

⇩ ⇧ ⤊

Maintenant que nous savons déterminer (avec un algorithme assez peu performant) si un entier est premier ou pas, nous allons pouvoir réaliser les trois premières étapes de RSA :

Etape 1 : choisir deux nombres entiers p et q de b bits.

Etape 2 : calculer le module de chiffrement n.

n = p * q

Etape 3 : calculer indicatrice d'Euler φ

φ = (p-1) * (q-1)

Commençons par nous souvenir qu'avec b bits, on peut encoder un entier naturel dont la valeur varie de 0 à 2^b - 1 , soit 2^b entiers au total.

On veut créer un nombre qui nécessite vraiment b bits et qui ne soit pas zéro : il faut donc que le bit de poids fort et le bit de poids faible ne soient pas 0 : 1-------1 .

Au minimum : seuls ces deux bits sont à 1. On a alors 2^b-1 + 1 .
Au maximum : tous les bits sont à 1. On a alors la valeur maximale 2^b - 1

Si on désire créer un nombre premier aléatoire de b bits, il suffit naïvement d'utiliser cet algorithme (on ne considèrera pas le cas où 2 est un premier possible, puisqu'on désire générer des grands nombres):

La fonction trouver_premier(b)

Calcule le plus petit et le plus grand nombre possible
Tire un nombre aléatoire IMPAIR entre ces deux nombres
Renvoie le premier nombre premier qu'on trouve à partir de ce nombre IMPAIR

24 - programmation et bugs° Mettre ce programme en mémoire.

"""
Module maison de chiffrement RSA. Non sécurisé. Maison quoi...
Contact : www.infoforall.fr
Email : contact@infoforall.fr
"""
 
# Importations
 
import random as rd
import math
 
# CONSTANTES : aucune
 
# Déclaration des fonctions internes pour l'étape 1
 
def est_premier_v2(x:int) -> bool:
    """Fonction naïve qui recherche si un nombre est premier par force brute
 
    :: param x(int)   :: un entier positif
    :: return (bool)  :: True si x est premier, False sinon
    .. ATTENTION : cette version disfonctionne si elle n'est pas modifée
 
    :: exemples ::
    >>> est_premier_v2(7)
    True
    >>> est_premier_v2(5)
    True
    >>> est_premier_v2(25)
    False
    >>> est_premier_v2(4)
    False
    >>> est_premier_v2(11)
    True
    >>> est_premier_v2(15)
    False
 
    """
 
    assert type(x) == int
    if x == 2:  # si x vaut 2, on renvoie True
        reponse = True
    elif x % 2 == 0:  # sinon si x est pair, on renvoie False
        reponse = False
    else:  # sinon, il faut chercher
        d = 3
        r = math.floor(math.sqrt(x))
        while x % d != 0 and d <= r:
            d = d + 2
        if d <= r:  # il y a bien un diviseur avant x
            reponse = False
        else:
            reponse = True
    return reponse
 
def nombre_impair(minimum:int, maximum:int) -> int:
    """Renvoie un nombre impair aléatoire dans [minimum ; maximum]
 
    :: param minimum(int)  :: le plus petit entier IMPAIR voulu
    :: param maximum(int)  :: le plus grand entier IMPAIR voulu
    :: return (int)        :: un entier IMPAIR aléatoire, dans [minimum ; maximum]
 
    """
 
    while x % 2 == 0 or x < minimum or x > maximum:
        x = rd.randint(minimum, maximum)
        if x % 2 == 0:
            x = x + 1
    return x
 
def renvoyer_premier(b:int) -> int:
    """Renvoie un nombre premier aléatoire de b bits compris entre les deux extrêmes 2**(b-1) + 1 et 2**b - 1"""
 
    assert b > 1
    pass

Lancer l'appel suivant puis corriger l'erreur qui apparaît.


>>> est_premier_v2(13)
True
 
>>> est_premier_v2(23)
True
 
>>> nombre_impair(13, 23)
    while x % 2 == 0 or x < minimum or x > maximum:
UnboundLocalError: local variable 'x' referenced before assignment

Correction ?

...CORRECTION...

Encore une erreur typique avec les boucles non bornées dans Python : on crée une condition avec une variable qui va évoluer lors du déroulement de la boucle mais qui n'existe pas initialement.

Ici, il faut donc donner à x une valeur qui permette de rentrer une première fois dans la boucle.

Il faudra donc que x ne respecte pas l'une des 3 conditions du TANT QUE. Facile du coup. Prenons 0 comme valeur de départ, de toutes manières, on tire un numéro aléatoire dès qu'on arrive ligne 65.

def nombre_impair(minimum:int, maximum:int) -> int:
    """Renvoie un nombre impair aléatoire dans [minimum ; maximum]
 
    :: param minimum(int)  :: le plus petit entier IMPAIR voulu
    :: param maximum(int)  :: le plus grand entier IMPAIR voulu
    :: return (int)        :: un entier IMPAIR aléatoire, dans [minimum ; maximum]
 
    """
 
    x = 0  # Initialisation de la variable de boucle du TANT QUE !    
    while x % 2 == 0 or x < minimum or x > maximum:
        x = rd.randint(minimum, maximum)
        if x % 2 == 0:
            x = x + 1
    return x

Finalisons.

Algorithme pour obtenir un nombre premier au hasard

Remarque : l'algorithme utilise

la fonction est_premier, ici dans sa version 2.
la fonction nombre_impair(minimum, maximum) qui renvoie un nombre impair aléatoire dans l'intervalle [minimum, maximum]

Description de l'algorithme de recherche renvoyer_premier(b)

minimum ← le plus petit nombre IMPAIR voulu (2^b-1 + 1)

maximum ← le plus grand nombre IMPAIR voulu (2^b - 1)

x ← nombre_impair(minimum, maximum)

TANT QUE NON est_premier_v2(x)

x ← x + 2

SI x > maximum

x ← minimum

Fin SI

Fin TANT QUE

Renvoyer x

25° Réaliser l'implémentation de la fonction renvoyer_premier.

Correction ?

...CORRECTION...

def renvoyer_premier(b:int) -> int:
    """Renvoie un nombre premier aléatoire de b bits compris entre les deux extrêmes 2**(b-1) + 1 et 2**b - 1"""
 
    minimum = 2**(b-1) + 1  # c'est un nombre impair
    maximum = 2**b - 1      # c'est un nombre impair aussi
    x = nombre_impair(minimum, maximum)  # x est impair
 
    while not est_premier_v2(x):
        x = x + 2
        if x > maximum:
            x = minimum
    return x

Ouf. Presque fini avec l'étape 1, 2 et 3 :

Structure d'un programme ou d'un module

On place les éléments dans un ordre précis et en séparant clairement les parties :

les importations
les CONSTANTES éventuelles
les déclarations de Classes
les déclarations de fonctions en séparant si possible :

les fonctions internes (pas d'appel depuis l'extérieur)
les fonctions d'interface (utilisables)

le programme qu'on veut voir s'exécuter uniquement en cas d'appel direct

Voici ci-dessous le programme permettant de (presque) gérer les étapes 1, 2 et 3.

26° Observer la fonction creer_cles puis lancer le programme. Observer les erreurs d'exécution fournies par le module doctest.

Questions

Où se trouve l'appel de la fonction creer_cles ?
Sous quelle condition cet appel ne se fera-t-il pas ?
Modifier alors les deux fonctions problématiques jusqu'à résolution du problème.

"""
Module maison de chiffrement RSA. Non sécurisé. Maison quoi...
Contact : www.infoforall.fr
Email : contact@infoforall.fr
"""
 
# Importations
 
import random as rd
import math
 
# CONSTANTES : aucune
 
# Déclaration des fonctions internes pour l'étape 1
 
def est_premier_v2(x:int) -> bool:
    """Fonction naïve qui recherche si un nombre est premier par force brute
 
    :: param x(int)   :: un entier positif
    :: return (bool)  :: True si x est premier, False sinon
    .. ATTENTION : cette version disfonctionne si elle n'est pas modifée
 
    :: exemples ::
    >>> est_premier_v2(7)
    True
    >>> est_premier_v2(5)
    True
    >>> est_premier_v2(25)
    False
    >>> est_premier_v2(4)
    False
    >>> est_premier_v2(11)
    True
    >>> est_premier_v2(15)
    False
 
    """
 
    assert type(x) == int
    if x == 2:  # si x vaut 2, on renvoie True
        reponse = True
    elif x % 2 == 0:  # sinon si x est pair, on renvoie False
        reponse = False
    else:  # sinon, il faut chercher
        d = 3
        r = math.floor(math.sqrt(x))
        while x % d != 0 and d <= r:
            d = d + 2
        if d <= r:  # on est sorti avant d'avoir atteint r
            reponse = False
        else:
            reponse = True
    return reponse
 
def nombre_impair(minimum:int, maximum:int) -> int:
    """Renvoie un nombre impair aléatoire dans [minimum ; maximum]
 
    :: param minimum(int)  :: le plus petit entier IMPAIR voulu
    :: param maximum(int)  :: le plus grand entier IMPAIR voulu
    :: return (int)        :: un entier IMPAIR aléatoire, dans [minimum ; maximum]
 
    """
 
    x = 0
    while x % 2 == 0 or x < minimum or x > maximum:
        x = rd.randint(minimum, maximum)
        if x % 2 == 0:
            x = x + 1
    return x
 
def renvoyer_premier(b:int) -> int:
    """Renvoie un nombre premier aléatoire de b bits compris entre les deux extrêmes 2**(b-1) + 1 et 2**b - 1"""
 
    minimum = 2**(b-1) + 1  # c'est un nombre impair
    maximum = 2**b - 1      # c'est un nombre impair aussi
    x = nombre_impair(minimum, maximum)  # x est impair
 
    while not est_premier_v2(x):
        x = x + 2
        if x > maximum:
            x = minimum
    return x
 
# Fonctions internes : pour l'étape 2
 
def calculer_module(p:int, q:int) -> int:
    """Renvoie le module n = p * q
 
    :: param p(int)   :: un nombre premier
    :: param q(int)   :: un deuxième nombre premier
    :: return (int)   :: le résultat de p * q
 
    >>> calculer_module(5, 7)
    35
 
    """
 
    return 0
 
# Fonctions internes : pour l'étape 3
 
def calculer_indicatrice(p:int, q:int) -> int:
    """Renvoie l'indicatrice d'Euler φ = (p-1) * (q-1)
 
    :: param p(int)   :: un nombre premier
    :: param q(int)   :: un deuxième nombre premier
    :: return (int)   :: le résultat de (p-1) * (q-1)
 
    >>> calculer_indicatrice(5, 7)
    24
 
    """
 
    return 0
 
# Fonctions d'interface
 
def creer_cles(b:int) -> tuple:
    """Renvoie un tuple contenant la clé publique et la clé privée"""
 
    # Etape 1 - choisir deux nombres premiers
    p = renvoyer_premier(b)
    q = renvoyer_premier(b)
    while p == q:
        q = renvoyer_premier(b)
 
    # Etape 2 - calculer le module de chiffrement
    n = calculer_module(p, q)
 
    # Etape 3 - déterminer l'indicatrice d'Euler
    φ = calculer_indicatrice(p, q)
 
    # Etape 4 - choisir un exposant de chiffrement et créer la clé publique
    e = 0
    cpub = (n, e)
 
    # Etape - déterminer l'exposant de déchiffrement et créer la clé privée
    d = 0
    cpri = (n, d)
 
    # Renvoyer les clés
    return (cpub, cpri)
 
# Instructions du programme principal de test si utilisation en appel direct (pas en importation)
if __name__ == '__main__':
    import doctest
    doctest.testmod()
    nb_bits = 20
    cpub, cpri = creer_cles(nb_bits)

Correction ?

...CORRECTION...

Où se trouve l'appel de la fonction creer_cles ? Dans le programme principal, en ligne 149.
Sous quelle condition cet appel ne se fera-t-il pas ? Si on importe ce programme en tant que module (voir la ligne 145)
Modifier alors les deux fonctions problématiques jusqu'à résolution du problème : voir la partie suivante mais bon...

6 - Tester

⇩ ⇧ ⤊

Avant de continuer, voyons comment vérifier le bon déroulement du programme même si un utilisateur envoie un mauvais argument à l'une des fonctions d'interface.

Nous allons revoir qu'on gère différemment

les fonctions d'interface : l'utilisateur a potentiellement envoyé n'importe quoi, il convient donc de vérifier les paramètres avant de demander aux fonctions internes de travailler sur ces données.
les fonctions internes : normalement, ces fonctions ont été testées et validées avant utilisation, si on leur transmet de bons arguments, pas de raison qu'elles dysfonctionnent.

Tester les fonctions avec des assertions

Première façon de faire : on stoppe l'exécution du programme

si l'une des préconditions est fausse (conditions sur les paramètres d'ENTREES)
si l'une des postconditions est fausse (conditions sur la réponse en SORTIE)

Avantage : on surveille tout et on détecte tous les dysfonctionnements qu'on peut tenter de gérer ensuite

Désavantage : ça coupe tout au moindre problème et ça ralentit le tout à cause du nombre importants de tests.

On peut voir cela comme de la programmation "offensive" : on accepte de travailler qu'avec des données valides et on refuse de continuer au moindre problème. Ca peut être bien sur certaines applications où les problèmes engendrés peuvent être pires qu'une simple interruption.

27° Placer les deux fonctions suivantes en mémoire pour remplacer les votre.

En vous aidant de la première, créer des assertions pour la seconde fonction :

les préconditions AVANT de commencer à calculer phi.
vérifiez les deux postconditions suivantes APRES avec calculer phi mais avant de faire répondre la fonction :

phi est bien un entier et
phi < p*q

# Fonctions internes : pour l'étape 2
 
def calculer_module(p:int, q:int) -> int:
    """Renvoie le module n = p * q
 
    :: param p(int)   :: un grand nombre premier
    :: param q(int)   :: un deuxième grand nombre premier
    :: return (int)   :: le résultat de p * q
 
    >>> calculer_module(5, 7)
    35
 
    """
 
    # Préconditions
    assert type(p) == int, "p doit être un entier"
    assert type(q) == int, "q doit être un entier"
    assert p > 2, "p doit être supérieur à 2"
    assert q > 2, "q doit être supérieur à 2"
    assert p % 2 == 1, "p doit être impair"
    assert q % 2 == 1, "q doit être impair"
    assert est_premier_v2(p), "p n'est pas premier"
    assert est_premier_v2(q), "q n'est pas premier"
 
    n = p * q
 
    # Postconditions
    assert type(n) == int, "n devrait être un entier, ce n'est pas le cas"
    assert n % 2 == 1, "n devrait être impair, ce n'est pas le cas..."
 
    return n
 
# Fonctions internes : pour l'étape 3
 
def calculer_indicatrice(p:int, q:int) -> int:
    """Renvoie l'indicatrice d'Euler φ = (p-1) * (q-1)
 
    :: param p(int)   :: un nombre premier
    :: param q(int)   :: un deuxième nombre premier
    :: return (int)   :: le résultat de (p-1) * (q-1)
 
    >>> calculer_indicatrice(5, 7)
    24
 
    """
 
    phi = (p-1) * (q-1)
    return phi

28° Tester si p et q sont premiers est-il rapide ou lent ?

Est-ce bien utile d'ailleurs pour une fonction qui est juste censée renvoyer une multiplication ?

Correction ?

...CORRECTION...

Ce test va être long, nous l'avons vu.

D'ailleurs, si le programme est exécuté dans le bon sens, n et p sont fournis par une autre fonction qui elle, doit garantir de renvoyer des nombres premiers.

Conclusion sur l'utilisation des assertions

Tout vérifier est contre-productif. Il faut vérifier ce qui est important pour la fonction en elle-même, sans oublier qu'elle s'insère dans un ensemble.

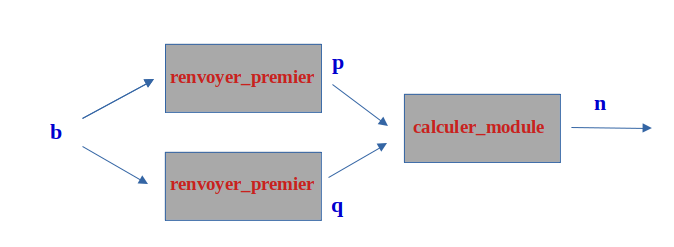
29° Pourquoi n'est-ce pas la peine de vérifier la primalité de p et q dans calculer_module si on a bien vérifié la fonction renvoyer_premier ?

Correction ?

...CORRECTION...

Si on a vérifié que renvoyer_premier renvoie bien un premier, inutile de lui redemander une deuxième fois. En plus, si elle a mal répondu la première fois, elle redira pareil la deuxième fois !

Habituellement (sauf exception), on va donc supprimer une bonne partie des asertions après la phase de développement. En garder quelques unes bien choisies permet de détecter plus facilement les dysfonctionnements pour une cause non prévue si on a pas montrer la correction de toutes les fgonctions.

Une fois toutes les fonctions internes validées, il ne reste qu'à bien filtrer les arguments envoyés aux fonctions d'interface.

Filtrer les paramètres des fonctions d'interface (hors programme, simple présentation de culture générale)

Avec les fonctions d'interface, c'est plus compliqué : le contenu des paramètres est potentiellement mauvais.

Soit on met des assertions : tant pis pour l'utilisateur qui fait n'importe quoi (on protège les données). Mais ça fait stopper le système.

def creer_cles(b:int) -> tuple:
    """Renvoie un tuple contenant la clé publique et la clé privée ou None
 
    :: param b(int)        :: le nombre de bits voulus pour les entiers premiers
    :: return (tuple|None) :: un tuple contenant les clés ou None en cas de problème
 
    """
 
    assert type(b) == int, "b n'est pas un entier"
    assert b > 0
 
    .. code normal ..

Soit on fait des tests d'erreurs (avec des if) sur les erreurs d'entrée qu'on peut prévoir, et on réalise autre chose que la séquence normale si c'est le cas. Il faut penser à tout et dire à l'utilisateur qu'on va renvoyer un mauvais résultat s'il envoie n'importe quoi... Est-ce mieux ?

def creer_cles(b:int) -> tuple:
    """Renvoie un tuple contenant la clé publique et la clé privée ou None
 
    :: param b(int)        :: le nombre de bits voulus pour les entiers premiers
    :: return (tuple|None) :: un tuple contenant les clés ou None en cas de problème
 
    """
 
    if type(b) == int and b > 0:
 
        ... code normal...
 
    else:
 
        return None

Soit on tente de faire fonctionner le système (avec des try) et en cas déclenchement d'une erreur, on prévoit autre chose (avec des except). Mais on n'en parlera pas plus que ça, ce n'est pas au programme et il faut faire attention à ce qu'on fait aussi : si on envoie un flottant, ça passera ici ! Je n'en parle qu'en terme de culture générale, pour que vous sachiez ce que cela fait si vous tombez sur un tel code. On en parlera plus ensuite.

def creer_cles(b:int) -> tuple:
    """Renvoie un tuple contenant la clé publique et la clé privée ou None
 
    :: param b(int)        :: le nombre de bits voulus pour les entiers premiers
    :: return (tuple) :: un tuple contenant les clés
    .. on utilisera des premiers sur 20 bits en cas de problème quelconque
 
    """
 
    try:
        b = int(b)
    except:
        b = 20
 
    if not b > 0:
        b = 20
 
 
    .. code normal ..

Le problème des méthodes 2 et 3 : il n'y pas toujours facile de retrouver la raison initiale d'une erreur à un moment si on a modifier les 'mauvaises' données envoyées par l'utilisateur. Bref, comme vous le voyez c'est un vrai sujet qui mérite des heures de formation.

A retenir pour cette année :

On distinguera 3 grands types d'erreur :

les erreurs de syntaxe : facile à détecter par l'interpréteur (on a oublié un :, on a écrit dec plutôt que def...)
les erreurs d'exécution : le code est "propre" mais l'un des contenus n'est pas du bon type ou ne contient pas ce qu'il faut. Il faut vérifier le contenu des variables pour savoir d'où vient le problème. Et si on a trop filtrer les arguments, il est possible que cela soit encore plus difficile !
Les erreurs logiques ou sémantiques : le code a l'air propre mais l'algorithme est faux. Cela ne déclenche pas d'erreur mais renvoie de mauvaises réponses. Comme elles ne déclenchent pas d'erreur en elles-même, ces erreurs sont compliquées à gérer. C'est l'un qu'un bon choix d'assertions permet de couper le programme à l'endroit où les préconditions ou postconditions ne sont plus bonnes.

Quelques bonnes pratiques pour limiter le nombre d'erreurs :

Faire de petites fonctions ET les tester avant de passer à autre chose : c'est l'intéret des jeux de tests
Placer des assertions permettant de vérifer les préconditions et les postconditions (cela coupe le déroulement du processus lorsqu'on détecte un problème)
Choisir judicieusement les assertions en prenant en compte la position de la fonction dans le programme ou le module (fonction d'interface, fonction interne...)
Le filtrage des paramètres est possible mais nécessite des précautions et n'est pas une solution miracle non plus : cela peut même compliquer la recherche de la source d'un bug.

7 - Déterminer l'exposant e de chiffrement

⇩ ⇧ ⤊

Rappel :

Etape 4 : choisir l'exposant de chiffrement e

Cette étape est plus délicate à réaliser. Nous allons voir qu'il va falloir utiliser l'algorithme d'Euclide.

Sans un bon algorithme, cette simple recherche peut prendre du temps.

Ce exposant de chiffrement e doit être

un entier inférieur à φ
premier avec φ : e ne doit pas partager de diviseur commun avec φ , d'où l'algorithme d'Euclide.

Ici, on a φ = 2016 et on décompose 2106 de cette façon : 2016 = 2⁵ * 3² * 7 : 2, 3 et 7 sont donc les diviseurs à ne pas prendre pour e.

Il suffit donc de prendre un nombre e qui ne soit divisible ni par 2, ni par 3, ni par 7.

Le plus grand commun diviseur de deux nombres premiers entre eux est donc ... 1 !

Il existe donc de nombreuses valeurs admissibles de e. Ces valeurs dépendent uniquement de φ (et donc indirectement de p et q).

Commençons par voir comment fonctionne l'algorithme d'Euclide qui permet de déterminer le plus grand commun diviseur (PGCD) entre deux entiers.

Le principe est de diviser un dividence par un diviseur pour trouver le reste.

Le diviseur devient alors le dividence et le reste devient le diviseur.

Si avant de faire la division, on voit que le diviseur est 0, on renvoie le dividence et il s'agit alors du PGCD.

Cherchons le plus grand commun diviseur de 20 et 12 :

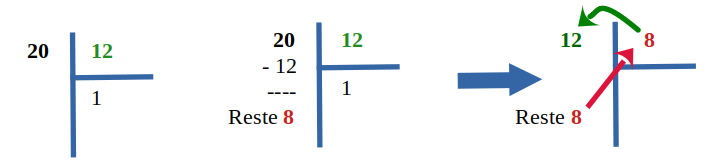
Le reste (qui est devenu le diviseur 8 maintenant) n'est pas nul, on continue.

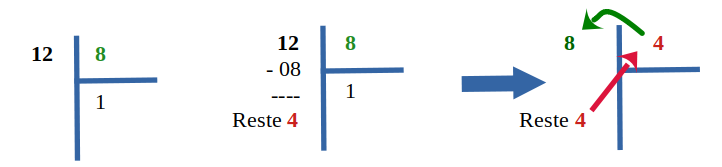
Le reste (qui est devenu le diviseur 4 maintenant) n'est pas nul, on continue.

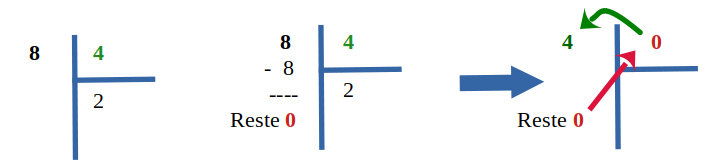
Le reste (qui est devenu le diviseur 0 maintenant) est nul : on arrête et on renvoie le nouveau dividende qui est le ... dernier diviseur non nul.

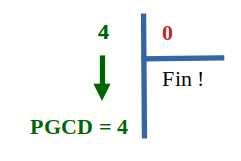
C'est bien la bonne réponse puisque 20 = 4 * 5 et que 12 = 3 * 4. 4 est bien le Plus Grand Commun Diviseur.

Notez bien qu'avec Python, ce sera simple à coder puisqu'on peut obtenir le reste directement.


>>> 20 % 12
8
 
>>> 12 % 8
4
 
>>> 8 % 4
0

Si vous voulez un deuxième exemple, vous pouvez trouvez ci-dessous la recherche de PGCD de 1416481 et 198434 :

Deuxième exemple ?

...DEUXIEME EXEMPLE...

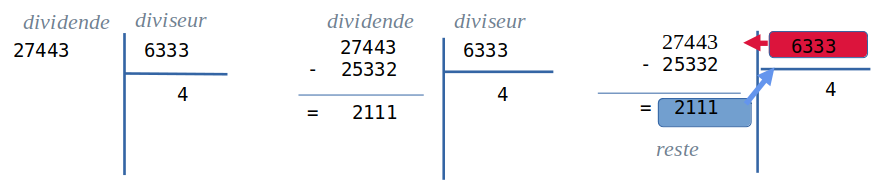
Cette fois, on atteint la configuration d'un diviseur nul.

On arrête la boucle non bornée et on renvoie le dividende actuel : 2111.

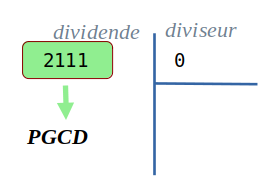
Le principe de l'algorithme est simple à appliquer (je ne parlerai pas des justifications, et démonstration ici)

Algorithme d'Euclide

BUT

Renvoyer le plus grand commun diviseur de deux nombres entiers.

Si on travaille avec :

1614915 qu'on peut décomposer sous cette forme 5 * 9 * 17 * 2111 de multiplication d'entiers et
25455706711 dont la décomposition est 23 * 2111 * 524287
le plus grand commun diviseur est 2111

ENTREES

Deux nombres a et b

Préconditions

Ce sont bien des entiers
Si a < b, on rajoute juste une étape supplémentaire : l'algorithme parvient automatiquement à inverser a et b !

Description de l'algorithme

dividende ← a

diviseur ← b

TANT QUE diviseur est différent de 0

reste ← dividende % diviseur

dividende ← diviseur

on remplace le dividence par l'ancien diviseur

diviseur ← reste

on remplace le diviseur par le reste obtenu

Fin TANT QUE

Renvoyer dividende

on renvoie donc le diviseur ayant mené à un reste nul

30-programmation et bugs°Réaliser l'implémentation de l'algorithme via la fonction pgcd en ligne 100 : quelqu'un vous a déjà tapé deux lignes de code pour récupérer a et b. Il vous suffit donc de remplacer le pass par l'implémentation du while.

Votre fonction doit passer les tests.

Attention, une faute d'inattention se cache dans les quelques lignes déjà tapées. Mais les jeux de tests devraient vous dire clairement ce qui ne va pas.

"""
Module maison de chiffrement RSA. Non sécurisé. Maison quoi...
Contact : www.infoforall.fr
Email : contact@infoforall.fr
"""
 
# Importations
 
import random as rd
import math
 
# CONSTANTES : aucune
 
# Déclaration des fonctions internes pour l'étape 1
 
def est_premier_v2(x:int) -> bool:
    """Fonction naïve qui recherche si un nombre est premier par force brute
 
    :: param x(int)   :: un entier positif
    :: return (bool)  :: True si x est premier, False sinon
    .. ATTENTION : cette version disfonctionne si elle n'est pas modifée
 
    :: exemples ::
    >>> est_premier_v2(7)
    True
    >>> est_premier_v2(5)
    True
    >>> est_premier_v2(25)
    False
    >>> est_premier_v2(4)
    False
    >>> est_premier_v2(11)
    True
    >>> est_premier_v2(15)
    False
 
    """
 
    assert type(x) == int
    if x == 2:  # si x vaut 2, on renvoie True
        reponse = True
    elif x % 2 == 0:  # sinon si x est pair, on renvoie False
        reponse = False
    else:  # sinon, il faut chercher
        d = 3
        r = math.floor(math.sqrt(x))
        while x % d != 0 and d <= r:
            d = d + 2
        if d <= r:  # on est sorti avant d'avoir atteint r
            reponse = False
        else:
            reponse = True
    return reponse
 
def nombre_impair(minimum:int, maximum:int) -> int:
    """Renvoie un nombre impair aléatoire dans [minimum ; maximum]
 
    :: param minimum(int)  :: le plus petit entier IMPAIR voulu
    :: param maximum(int)  :: le plus grand entier IMPAIR voulu
    :: return (int)        :: un entier IMPAIR aléatoire, dans [minimum ; maximum]
 
    """
 
    x = 0
    while x % 2 == 0 or x < minimum or x > maximum:
        x = rd.randint(minimum, maximum)
        if x % 2 == 0:
            x = x + 1
    return x
 
def renvoyer_premier(b:int) -> int:
    """Renvoie un nombre premier aléatoire de b bits compris entre les deux extrêmes 2**(b-1) + 1 et 2**b - 1"""
 
    minimum = 2**(b-1) + 1  # c'est un nombre impair
    maximum = 2**b - 1      # c'est un nombre impair aussi
    x = nombre_impair(minimum, maximum)  # x est impair
 
    while not est_premier_v2(x):
        x = x + 2
        if x > maximum:
            x = minimum
    return x
 
# Fonctions internes : pour l'étape 2
 
def calculer_module(p:int, q:int) -> int:
    """Renvoie le module n = p * q"""
 
    return p * q
 
# Fonctions internes : pour l'étape 3
 
def calculer_indicatrice(p:int, q:int) -> int:
    """Renvoie l'indicatrice d'Euler φ = (p-1) * (q-1)"""
 
    return (p-1) * (q-1)
 
# Fonctions internes : pour l'étape 4
 
def pgcd(a, b):
    """Renvoie le plus grand diviseur commun de deux entiers a et b
 
    (ALGO EUCLIDE VERSION EXPLICITE) 
    :: param a(int) :: l'un des deux nombres
    :: param b(int) :: l'un des deux nombres
    :: return (int) :: le PGCD
 
    :: exemple ::
    >>> pgcd(500, 200)
    100
    >>> pgcd(5, 20)
    5
    >>> pgcd(5, 21)
    1
    >>> pgcd(15, 6)
    3
 
    """
 
    dividence = a
    diviseur = b
 
    pass
 
def euclide_bis(a:int, b:int) -> int:
    """Renvoie le plus grand diviseur commun de deux entiers a et b"""
 
    while b != 0:
       t = b
       b = a % b
       a = t
    return a
 
def choisir_e(phi):
    """Détermine un exposant de chiffrement e (pas forcement sécurisé) en utilisant le théorème d'Euclide"""
 
    e = rd.randint(5,phi-1)
    while pgcd(phi, e) != 1:  # Tant que e ne convient pas
        e = e + 1
        if e >= phi:  # si e ne peut plus convenir car trop grand
            e = rd.randint(5,phi-1)
 
    return e
 
# Fonctions internes : pour l'étape 5
 
def calculer_d_naif(e, phi):
    """Calcule d en utilisant juste les propriétés de e et d : (e*d) % phi = 1
 
    :: param e(int)   :: un exposant de chiffrement valide
    :: param phi(int) :: l'indicatrice d'Euler correspondante
    :: return (int)   :: un exposant de déchiffrement adapté
 
    """
 
    pass
 
def calculer_d(e, phi):
    """Calcule d en utilisant le théorème d'Euclide étendu
 
    :: param e(int)   :: un exposant de chiffrement valide
    :: param phi(int) :: l'indicatrice d'Euler correspondante
    :: return (int)   :: un exposant de déchiffrement adapté
 
    """
 
    a = e
    b = phi
    (r,u,v,rr,uu,vv) = (a,1,0,b,0,1)
    while rr != 0:
        q = r//rr
        (r,u,v,rr,uu,vv) = (rr,uu,vv, r-q*rr, u-q*uu, v-q*vv)
    while u <= 0:
        u = u + phi
    return u
 
# Fonctions d'interface
 
def creer_cles(b:int) -> tuple:
    """Renvoie un tuple contenant la clé publique et la clé privée"""
 
    # Etape 1
    p = renvoyer_premier(b)
    q = renvoyer_premier(b)
    while p == q:
        q = renvoyer_premier(b)
 
    # Etape 2
    n = calculer_module(p, q)
 
    # Etape 3
    φ = calculer_indicatrice(p, q)
 
    # Etape 4
    e = choisir_e(φ)
 
    # Etape 5
    d = calculer_d(e, φ)
 
    # Etape finale
    cpub = (n, e)
    cpri = (n, d)
    return (cpub, cpri)
 
# Programme
 
if __name__ == '__main__':
    import doctest
    doctest.testmod()

Correction ?

...CORRECTION...

def pgcd(a, b):
    """Renvoie le plus grand diviseur commun de deux entiers a et b
 
    (ALGO EUCLIDE VERSION EXPLICITE) 
    :: param a(int) :: l'un des deux nombres
    :: param b(int) :: l'un des deux nombres
    :: return (int) :: le PGCD
 
    :: exemple ::
    >>> pgcd(500, 200)
    100
    >>> pgcd(5, 20)
    5
    >>> pgcd(5, 21)
    1
    >>> pgcd(15, 6)
    3
 
    """
 
    dividende = a
    diviseur = b
 
    while diviseur != 0:
       reste = dividende % diviseur  # Le reste devient le diviseur
       dividende = diviseur
       diviseur = reste
 
    return dividende

Bug typique

Il s'agissait donc ici d'un mauvais nommage de variables

D'où l'intérêt d'utiliser les propositions automatiques qui s'affichent sur les bons éditeurs de code.

31° Observer euclide_bis. Les noms ne sont pas explicites cette fois : certaines préfèrent de telles versions "épurées" avec des noms courts. Le problème vient de la compréhension du code quelques semaines, mois ou années plus tard.

32° Votre fonction renvoie le plus grand commun diviseur. Quel doit être le PGCD de deux nombres premiers entre eux (tels que e et φ) ?

Correction ?

...CORRECTION...

Si deux nombres sont premiers entre eux, c'est qu'ils ne partagent aucun diviseur, à part le diviseur qu'ils ont tous : 1.

Le PGCD de deux nombres premiers entre eux est donc nécessairement 1.

Si il est plus grand, c'est que les deux nombres ne sont pas premiers entre eux.

33° Expliquer comment fonctionne choisir_e pour renvoyer un exposant valable.

34° Observer et comprendre creer_cles. Lancer quelques tests pour vérifier son bon fonctionnement.

Remarque : d est déterminé par une fonction que vous n'avez pas codé vous-même pour le moment.

8 - Déterminer l'exposant d de déchiffrement

⇩ ⇧ ⤊

Voici le code si vous redemarrez à partir d'ici pendant une nouvelle séance et que vous n'êtes plus certain d'avoir un code valide :

Code étapes 1 à 5

...CODE...

"""
Module maison de chiffrement RSA. Non sécurisé. Maison quoi...
Contact : www.infoforall.fr
Email : contact@infoforall.fr
"""
 
# Importations
 
import random as rd
import math
 
# CONSTANTES : aucune
 
# Déclaration des fonctions internes pour l'étape 1
 
def est_premier_v2(x:int) -> bool:
    """Fonction naïve qui recherche si un nombre est premier par force brute
 
    :: param x(int)   :: un entier positif
    :: return (bool)  :: True si x est premier, False sinon
    .. ATTENTION : cette version disfonctionne si elle n'est pas modifée
 
    :: exemples ::
    >>> est_premier_v2(7)
    True
    >>> est_premier_v2(5)
    True
    >>> est_premier_v2(25)
    False
    >>> est_premier_v2(4)
    False
    >>> est_premier_v2(11)
    True
    >>> est_premier_v2(15)
    False
 
    """
 
    assert type(x) == int
    if x == 2:  # si x vaut 2, on renvoie True
        reponse = True
    elif x % 2 == 0:  # sinon si x est pair, on renvoie False
        reponse = False
    else:  # sinon, il faut chercher
        d = 3
        r = math.floor(math.sqrt(x))
        while x % d != 0 and d <= r:
            d = d + 2
        if d <= r:  # on est sorti avant d'avoir atteint r
            reponse = False
        else:
            reponse = True
    return reponse
 
def nombre_impair(minimum:int, maximum:int) -> int:
    """Renvoie un nombre impair aléatoire dans [minimum ; maximum]
 
    :: param minimum(int)  :: le plus petit entier IMPAIR voulu
    :: param maximum(int)  :: le plus grand entier IMPAIR voulu
    :: return (int)        :: un entier IMPAIR aléatoire, dans [minimum ; maximum]
 
    """
 
    x = 0
    while x % 2 == 0 or x < minimum or x > maximum:
        x = rd.randint(minimum, maximum)
        if x % 2 == 0:
            x = x + 1
    return x
 
def renvoyer_premier(b:int) -> int:
    """Renvoie un nombre premier aléatoire de b bits compris entre les deux extrêmes 2**(b-1) + 1 et 2**b - 1"""
 
    minimum = 2**(b-1) + 1  # c'est un nombre impair
    maximum = 2**b - 1      # c'est un nombre impair aussi
    x = nombre_impair(minimum, maximum)  # x est impair
 
    while not est_premier_v2(x):
        x = x + 2
        if x > maximum:
            x = minimum
    return x
 
# Fonctions internes : pour l'étape 2
 
def calculer_module(p:int, q:int) -> int:
    """Renvoie le module n = p * q"""
 
    return p * q
 
# Fonctions internes : pour l'étape 3
 
def calculer_indicatrice(p:int, q:int) -> int:
    """Renvoie l'indicatrice d'Euler φ = (p-1) * (q-1)"""
 
    return (p-1) * (q-1)
 
# Fonctions internes : pour l'étape 4
 
def pgcd(a, b):
    """Renvoie le plus grand diviseur commun de deux entiers a et b
 
    (ALGO EUCLIDE VERSION EXPLICITE) 
    :: param a(int) :: l'un des deux nombres
    :: param b(int) :: l'un des deux nombres
    :: return (int) :: le PGCD
 
    :: exemple ::
    >>> pgcd(500, 200)
    100
    >>> pgcd(5, 20)
    5
    >>> pgcd(5, 21)
    1
    >>> pgcd(15, 6)
    3
 
    """
 
    dividende = a
    diviseur = b
 
    while diviseur != 0:
       reste = dividende % diviseur  # Le reste devient le diviseur
       dividende = diviseur
       diviseur = reste
 
    return dividende
 
def euclide_bis(a:int, b:int) -> int:
    """Renvoie le plus grand diviseur commun de deux entiers a et b"""
 
    while b != 0:
       t = b
       b = a % b
       a = t
    return a
 
def choisir_e(phi):
    """Détermine un exposant de chiffrement e (pas forcement sécurisé) en utilisant le théorème d'Euclide"""
 
    e = rd.randint(5,phi-1)
    while pgcd(phi, e) != 1:  # Tant que e ne convient pas
        e = e + 1
        if e >= phi:  # si e ne peut plus convenir car trop grand
            e = rd.randint(5,phi-1)
 
    return e
 
# Fonctions internes : pour l'étape 5
 
def calculer_d_naif(e, phi):
    """Calcule d en utilisant juste les propriétés de e et d : (e*d) % phi = 1
 
    :: param e(int)   :: un exposant de chiffrement valide
    :: param phi(int) :: l'indicatrice d'Euler correspondante
    :: return (int)   :: un exposant de déchiffrement adapté
 
    """
 
    pass
 
def calculer_d(e, phi):
    """Calcule d en utilisant le théorème d'Euclide étendu
 
    :: param e(int)   :: un exposant de chiffrement valide
    :: param phi(int) :: l'indicatrice d'Euler correspondante
    :: return (int)   :: un exposant de déchiffrement adapté
 
    """
 
    a = e
    b = phi
    (r,u,v,rr,uu,vv) = (a,1,0,b,0,1)
    while rr != 0:
        q = r//rr
        (r,u,v,rr,uu,vv) = (rr,uu,vv, r-q*rr, u-q*uu, v-q*vv)
    while u <= 0:
        u = u + phi
    return u
 
# Fonctions d'interface
 
def creer_cles(b:int) -> tuple:
    """Renvoie un tuple contenant la clé publique et la clé privée"""
 
    # Etape 1
    p = renvoyer_premier(b)
    q = renvoyer_premier(b)
    while p == q:
        q = renvoyer_premier(b)
 
    # Etape 2
    n = calculer_module(p, q)
 
    # Etape 3
    φ = calculer_indicatrice(p, q)
 
    # Etape 4
    e = choisir_e(φ)
 
    # Etape 5
    d = calculer_d(e, φ)
 
    # Etape finale
    cpub = (n, e)
    cpri = (n, d)
    return (cpub, cpri)
 
# Programme
 
if __name__ == '__main__':
    import doctest
    doctest.testmod()

Etape 5 : trouver l'exposant de déchiffrement d (connaissant e et φ)

Ce exposant de déchiffrement d doit être l'inverse de e modulo φ.

Cela veut dire qu'il faut respecter cette condition : le reste de la division entière de (e*d) par φ vaut 1.

(e * d) % φ = 1

D'où la notion d'inverse "e = 1 / d".

Dans le cas de notre exemple :

Indicatrice d'Euler φ = 2016
Exposant de chiffrement e = 437
on détermine que l'exposant de déchiffrement est d = 1181

Vérification avec Python :


>>> e = 437
>>> d = 1181
>>> phi = 2016
>>> (e*d) % phi
1

Cette fois, il faudra utiliser l'algorithme d'Euclide étendu. Sinon, encore une fois, cela prendrait un temps énorme pour p et q de grande taille.

Nous n'allons pas l'étudier, il est déjà codé et fonctionnel ici.

Par contre, vous aller créer une fonction qui fait la même chose mais en version naïve et nous verrons que notre RSA maison ne fonctionnera plus trop bien sur cette dernière étape : trop lent pour de grandes clés.

35° Coder la fonction calculer_d_naif pour qu'elle renvoie la valeur de d en respectant cette technique :

Connaissant e et φ, tester toutes les valeurs possibles de d jusqu'à trouver celle qui répond à :

(e * d) % φ = 1

Correction ?

...CORRECTION...

def calculer_d_naif(e, phi):
    """Calcule d en utilisant juste les propriétés de e et d : (e*d) % phi = 1
 
    :: param e(int)   :: un exposant de chiffrement valide
    :: param phi(int) :: l'indicatrice d'Euler correspondante
    :: return (int)   :: un exposant de déchiffrement adapté
 
    """
 
    for d in range(3, phi):
        if (e*d) % phi == 1:
            return d

Prenons le premier exemple du cours :

p = 17
q = 127
n = 2159
φ = 2016
e = 437

La valeur de d est alors 1181.

36° Tester ceci pour voir que les deux fonctions fonctionnent :


>>> e = 437
>>> φ = 2016
>>> calculer_d(e,φ)
1181
 
>>> calculer_d_naif(e,φ)
1181

Voilà, vous avez codé de bout en bout la génération de clés RSA. Même la fin visiblement. Les oiseaux chantent, un arc-en-ciel apparâit, tout va bien dans le meilleur des mondes.

Prenons cet exemple :

p = 703837
q = 844127
n = 594127815299
φ = 594126267336
e = 135478415797

La valeur de d est alors 378707856781.

37° Tester ceci pour voir que les deux fonctions fonctionnent, ou de façon problématique pour l'une d'entre elles, devinez laquelle ;o) :


>>> e = 135478415797
>>> φ = 594126267336
>>> calculer_d(e,φ)
378707856781
 
>>> calculer_d_naif(e,φ)
378707856781

9 - Et avec un vrai fichier ?

⇩ ⇧ ⤊

Pas trop le temps de décrire cette partie qui mériterait un TP en lui-même.

Mais bon, maintenant que vous avez un moyen de générer de (petites) clés RSA, il est tenté de partager une clé publique avec quelqu'un que vous connaissez pour qu'il puisse vous transmettre des fichiers cryptés.

38 - documentation et programmation° Placer le gros programme suivant en mémoire. Ensuite, taper ceci dans la console pour comprendre comment fonctionne le chiffrement et le déchiffrement d'un fichier quelconque.


>>> cpub, cpri = creer_cles(20)
>>> cpub
(524019377303, 89243442031)
 
>>> cpri
(524019377303, 453869594791)
 
>>> help(chiffrer_fichier)
 
>>> help(dechiffrer_fichier)

Correction ?

...CORRECTION...


>>> help(chiffrer_fichier)

Help on function chiffrer_fichier in module __main__:
 
chiffrer_fichier(cle: tuple, fichier_base: str, fichier_chiffre: str, affichage: bool = False) -> None
    Chiffre le fichier_base avec la clé RSA cle en créant un fichier_chiffre
     
    :: param cle(tuple)           :: une clé RSA sous forme (module, exposant de chiffrement)
    :: param fichier_base(str)    :: le nom du fichier à chiffrer
    :: param fichier_chiffre(str) :: le nom du fichier chiffré qu'on veut créer
    :: param affichage(bool)      :: False par défaut, True pour afficher des indications sur le premier bloc
    :: return (None)              :: "fonction-procédure" Python
    .. ATTENTION                  .. Ecrasera l'ancien fichier_chiffre s'il existe déjà

 
>>> help(dechiffrer_fichier)

Help on function dechiffrer_fichier in module __main__:
 
dechiffrer_fichier(cle: tuple, fichier_chiffre: str, fichier_dechiffre: str, affichage: bool = False) -> None
    Déchiffre le fichier_chiffre avec la clé RSA cle en créant un fichier_dechiffre
     
    :: param cle(tuple)             :: une clé RSA sous forme (module, exposant de chiffrement)
    :: param fichier_chiffre(str)   :: le nom du fichier chiffré à déchiffrer
    :: param fichier_dechiffre(str) :: le nom du fichier déchiffré qu'on veut créer
    :: param affichage(bool)        :: False par défaut, True pour afficher des indications sur le premier bloc
    :: return (None)                :: "fonction-procédure" Python
    .. ATTENTION                    .. Ecrasera l'ancien fichier_dechiffre s'il existe déjà

"""
Module maison de chiffrement RSA. Non sécurisé. Maison quoi...
Contact : www.infoforall.fr
Email : contact@infoforall.fr
"""
 
# Importations
 
import random as rd
import math
 
# CONSTANTES : aucune
 
# Déclaration des fonctions internes pour l'étape 1
 
def est_premier_v2(x:int) -> bool:
    """Fonction naïve qui recherche si un nombre est premier par force brute
 
    :: param x(int)   :: un entier positif
    :: return (bool)  :: True si x est premier, False sinon
    .. ATTENTION : cette version disfonctionne si elle n'est pas modifée
 
    :: exemples ::
    >>> est_premier_v2(7)
    True
    >>> est_premier_v2(5)
    True
    >>> est_premier_v2(25)
    False
    >>> est_premier_v2(4)
    False
    >>> est_premier_v2(11)
    True
    >>> est_premier_v2(15)
    False
 
    """
 
    assert type(x) == int
    if x == 2:  # si x vaut 2, on renvoie True
        reponse = True
    elif x % 2 == 0:  # sinon si x est pair, on renvoie False
        reponse = False
    else:  # sinon, il faut chercher
        d = 3
        r = math.floor(math.sqrt(x))
        while x % d != 0 and d <= r:
            d = d + 2
        if d <= r:  # on est sorti avant d'avoir atteint r
            reponse = False
        else:
            reponse = True
    return reponse
 
def nombre_impair(minimum:int, maximum:int) -> int:
    """Renvoie un nombre impair aléatoire dans [minimum ; maximum]
 
    :: param minimum(int)  :: le plus petit entier IMPAIR voulu
    :: param maximum(int)  :: le plus grand entier IMPAIR voulu
    :: return (int)        :: un entier IMPAIR aléatoire, dans [minimum ; maximum]
 
    """
 
    x = 0
    while x % 2 == 0 or x < minimum or x > maximum:
        x = rd.randint(minimum, maximum)
        if x % 2 == 0:
            x = x + 1
    return x
 
def renvoyer_premier(b:int) -> int:
    """Renvoie un nombre premier aléatoire de b bits compris entre les deux extrêmes 2**(b-1) + 1 et 2**b - 1"""
 
    minimum = 2**(b-1) + 1  # c'est un nombre impair
    maximum = 2**b - 1      # c'est un nombre impair aussi
    x = nombre_impair(minimum, maximum)  # x est impair
 
    while not est_premier_v2(x):
        x = x + 2
        if x > maximum:
            x = minimum
    return x
 
# Fonctions internes : pour l'étape 2
 
def calculer_module(p:int, q:int) -> int:
    """Renvoie le module n = p * q"""
 
    return p * q
 
# Fonctions internes : pour l'étape 3
 
def calculer_indicatrice(p:int, q:int) -> int:
    """Renvoie l'indicatrice d'Euler φ = (p-1) * (q-1)"""
 
    return (p-1) * (q-1)
 
# Fonctions internes : pour l'étape 4
 
def pgcd(a, b):
    """Renvoie le plus grand diviseur commun de deux entiers a et b
 
    (ALGO EUCLIDE VERSION EXPLICITE) 
    :: param a(int) :: l'un des deux nombres
    :: param b(int) :: l'un des deux nombres
    :: return (int) :: le PGCD
 
    :: exemple ::
    >>> pgcd(500, 200)
    100
    >>> pgcd(5, 20)
    5
    >>> pgcd(5, 21)
    1
    >>> pgcd(15, 6)
    3
 
    """
 
    dividende = a
    diviseur = b
 
    while diviseur != 0:
       reste = dividende % diviseur  # Le reste devient le diviseur
       dividende = diviseur
       diviseur = reste
 
    return dividende
 
def choisir_e(phi):
    """Détermine un exposant de chiffrement e (pas forcement sécurisé) en utilisant le théorème d'Euclide"""
 
    e = rd.randint(5,phi-1)
    while pgcd(phi, e) != 1:  # Tant que e ne convient pas
        e = e + 1
        if e >= phi:  # si e ne peut plus convenir car trop grand
            e = rd.randint(5, phi-1)
 
    return e
 
# Fonctions internes : pour l'étape 5
 
def calculer_d(e, phi):
    """Calcule d en utilisant le théorème d'Euclide étendu"""
 
    a = e
    b = phi
    (r,u,v,rr,uu,vv) = (a,1,0,b,0,1)
    while rr != 0:
        q = r//rr
        (r,u,v,rr,uu,vv) = (rr,uu,vv, r-q*rr, u-q*uu, v-q*vv)
    while u <= 0:
        u = u + phi
    return u
 
# Fonctions internes de chiffrements / déchiffrement
 
def exp_rapide(m:int, cle:tuple) -> int:
    """Permet de calcul rapidement m**e % n par exponentiation rapide"""
 
    (n, e) = cle
    if e == 1:
        return m % n
    else:
        if e % 2 == 0:
            return exp_rapide(m**2 % n, (n, e//2)) % n
        else:
            return (m * exp_rapide(m**2 % n, (n, e//2))) % n
 
 
def est_valide(liste:list, n:int) -> bool :
    """Fonction booléen qui vérifie qu'aucune valeur dans la liste du message n'est trop grande"""
    for valeur in liste :
        if valeur >= n :
            return False
    return True
 
# Fonctions d'interface
 
def creer_cles(b:int) -> tuple:
    """Renvoie un tuple contenant la clé publique et la clé privée"""
 
    # Etape 1
    p = renvoyer_premier(b)
    q = renvoyer_premier(b)
    while p == q:
        q = renvoyer_premier(b)
 
    # Etape 2
    n = calculer_module(p, q)
 
    # Etape 3
    φ = calculer_indicatrice(p, q)
 
    # Etape 4
    e = choisir_e(φ)
 
    # Etape 5
    d = calculer_d(e, φ)
 
    # Etape finale
    cpub = (n, e)
    cpri = (n, d)
    return (cpub, cpri)
 
 
 
 
 
def chiffrer_message(m:int, cle:tuple) -> int:
    """Chiffre (ou déchiffre le message m en utilisant m**e % n en utilisant cle=(n,e)"""
    return exp_rapide(m, cle)
 
def chiffrer_tableau(tableau:list, cle:tuple) -> list :
    """Chiffre (ou déchiffre) les valeurs dans le tableau de valeurs à l'aide de la clé (n,e)"""
 
    (n, e) = cle
    if est_valide(tableau, n) :
        chiffrement = [exp_rapide(m, cle) % n for m in tableau]
        return chiffrement
    else :
        print(f'Echec : les valeurs à chiffrer doivent être inférieures à n = {n}')
        return []
 
def chiffrer_fichier(cle:tuple, fichier_base:str, fichier_chiffre:str, affichage:bool=False) -> None:
    """Chiffre le fichier_base avec la clé RSA cle en créant un fichier_chiffre
 
    :: param cle(tuple)           :: une clé RSA sous forme (module, exposant de chiffrement)
    :: param fichier_base(str)    :: le nom du fichier à chiffrer
    :: param fichier_chiffre(str) :: le nom du fichier chiffré qu'on veut créer
    :: param affichage(bool)      :: False par défaut, True pour afficher des indications sur le premier bloc
    :: return (None)              :: "fonction-procédure" Python
    .. ATTENTION                  .. Ecrasera l'ancien fichier_chiffre s'il existe déjà
 
    """
    assert fichier_base != fichier_chiffre, "Les deux noms de fichiers ne doivent pas être identiques"
    assert type(fichier_base) == str, "Le paramètre fichier_base doit être un string"
    assert type(fichier_chiffre) == str, "Le paramètre fichier_chiffre doit être un string"
    assert type(cle) == tuple, "Clé non valide : votre clé n'est pas un nuplet"
    assert type(cle[0]) == int, "Module de chiffrement non valide : il doit être un entier"
    assert type(cle[1]) == int, "Exposant non valide : il doit être un entier"
    assert cle[0] > cle[1], "Clé non valide : elle doit être sous la forme d'un nuplet (module, exposant)"
 
    # 1 - on détermine le nombre d'octets du bloc d'octets, adapté à n : m < n
    (n, e) = cle
    nb_lecture = math.floor(math.log(n)/math.log(256))  # Nb d'octets à lire d'un coup
    nb_ecriture = math.ceil(math.log(n)/math.log(256))  # Nb d'octets à écrire d'un coup
 
    # 2 - on crée ou écrase l'ancien contenu du fichier chiffré
    fc = open(fichier_chiffre, 'wb')
    fc.close()
 
    # 3 - on ouvre les deux fichiers en mode , l'un en lecture, l'autre en ajout/append
    fb = open(fichier_base, 'rb')
    fc = open(fichier_chiffre, 'ab')
 
    # 4 - on lit et chiffre les blocs du fichier de base tant qu'ils sont pas vides
    bloc = fb.read(nb_lecture)
    if affichage: print(f"Premier bloc d'octets dans le fichier : {bloc}")
    nb = 0
    prochain = 50000 # message tous les 10 ko
    print("Chiffrement en cours...")
    while bloc:
 
        # Affichage d'un petit message dans la console tous les 10 ko traités        
        nb = nb + nb_lecture
        if nb > prochain:
            print(f"{nb//50000*50} ko", end=" - ")
            prochain = prochain + 50000
 
        # On transforme les octets en tableau de valeurs 0-255
        t = list(bloc)
        if affichage: print(f"Bloc donnant ces valeurs 0-255 : {t}")
 
        # On calcule l'entier m représentant cette séquence de valeurs 
        m = 0
        for i in range(len(t)):
            m = m + t[i]*256**(nb_lecture-i-1)
        if affichage: print(f"Transformation de ces octets en m = {m}")
 
        # On chiffre ce message m
        mc = exp_rapide(m, cle) % n
        if affichage: print(f"Message codé mc = {mc}")
 
        # On transforme ce mc en un tableau de valeurs 0-255 à écrire
        tc = [(mc // 256**(nb_ecriture-x-1)) % 256 for x in range(nb_ecriture)]
        if affichage: print(f"Transformation en suite de valeurs 0-255 : {tc}")
 
        # On transforme ce tableau en octets
        bc = bytes(tc)  # pour bloc chiffré
        if affichage: print(f"Bloc d'octets chiffrant finalement ce bloc de départ : {bc}")
 
        # On écrit ces octets codés dans le fichier chiffré
        fc.write(bc)
 
        # On passe au bloc suivant dans le fichier de base
        bloc = fb.read(nb_lecture)
        if affichage: affichage = False
 
    # 5 - on ferme les deux fichiers
    fb.close()
    fc.close()
    print("\nChiffrement terminé")
 
def dechiffrer_fichier(cle:tuple, fichier_chiffre:str, fichier_dechiffre:str, affichage:bool=False) -> None:
    """Déchiffre le fichier_chiffre avec la clé RSA cle en créant un fichier_dechiffre
 
    :: param cle(tuple)             :: une clé RSA sous forme (module, exposant de chiffrement)
    :: param fichier_chiffre(str)   :: le nom du fichier chiffré à déchiffrer
    :: param fichier_dechiffre(str) :: le nom du fichier déchiffré qu'on veut créer
    :: param affichage(bool)        :: False par défaut, True pour afficher des indications sur le premier bloc
    :: return (None)                :: "fonction-procédure" Python
    .. ATTENTION                    .. Ecrasera l'ancien fichier_dechiffre s'il existe déjà
 
    """
 
    assert fichier_chiffre != fichier_dechiffre, "Les deux noms de fichiers ne doivent pas être identiques"
    assert type(fichier_chiffre) == str, "Le paramètre fichier_base doit être un string"
    assert type(fichier_dechiffre) == str, "Le paramètre fichier_chiffre doit être un string"
    assert type(cle) == tuple, "Clé non valide : votre clé n'est pas un nuplet"
    assert type(cle[0]) == int, "Module de chiffrement non valide : il doit être un entier"
    assert type(cle[1]) == int, "Exposant non valide : il doit être un entier"
    assert cle[0] > cle[1], "Clé non valide : elle doit être sous la forme d'un nuplet (module, exposant)"
 
 
    # 1 - on détermine le nombre d'octets du bloc d'octets, adapté à n : m < n
    (n, e) = cle
    nb_lecture = math.ceil(math.log(n)/math.log(256))    # Pour trouver jusqu'à n
    nb_ecriture = math.floor(math.log(n)/math.log(256))  # Pour adapter à m
 
    # 2 - on crée ou écrase l'ancien contenu du fichier déchiffré
    fd = open(fichier_dechiffre, 'wb')
    fd.close()
 
    # 3 - on ouvre les deux fichiers en mode bytes
    fc = open(fichier_chiffre, 'rb')  # en mode lecture seule
    fd = open(fichier_dechiffre, 'ab')  # en mode ajout-append
 
    # 4 - on lit et déchiffre les blocs du fichier chiffré tant qu'ils sont pas vides
    bloc = fc.read(nb_lecture)
    if affichage: print(bloc)
    nb = 0
    prochain = 50000 # message tous les 10 ko
    print("Déchiffrement en cours...")
 
    while bloc:
 
        # Affichage d'un petit message dans la console tous les 10 ko traités
        nb = nb + nb_lecture
        if nb > prochain:
            print(f"{nb//50000*50} ko", end=" - ")
            prochain = prochain + 50000
 
        # On transforme les octets en tableau de valeurs 0-255
        t = list(bloc)
        if affichage: print(t)
 
        # On transforme ces valeurs successives en un entier mc
        mc = 0
        for i in range(len(t)):
            mc = mc + t[i]*256**(nb_lecture-i-1)
        if affichage: print(mc)
 
        # On décode le message
        md = exp_rapide(mc, cle) % n
        if affichage: print(md)
 
        # On transforme ce message décodé en un tableau de valeurs 0-255        
        td = [(md // 256**(nb_ecriture-x-1)) % 256 for x in range(nb_ecriture)]
        if affichage: print(td)
 
        # On transforme ce tableau en octets-bytes
        bd = bytes(td)
        if affichage: print(bd)
 
        # On écrit ces octets dans le fichier déchiffré
        fd.write(bd)
 
        # On passe au bloc suivant dans le fichier chiffré
        bloc = fc.read(nb_lecture)
        if affichage: affichage = False
 
    # 5 - On ferme les deux fichiers
    fc.close()
    fd.close()
    print("\nDéchiffrement réalisé")
 
 
def prog_test():
 
    b = 20
    cpub, cpri = creer_cles(b)

Voici un exemple d'utilisation :


>>> cpub, cpri = creer_cles(20)
>>> cpub
(501751207679, 233074674377)
 
>>> cpri
(501751207679, 316864673033)
>>> chiffrer_fichier(cpub, "test.png", "chiffre.png")
 
Chiffrement en cours...
50 ko - 100 ko - 150 ko - 200 ko -
Chiffrement terminé
>>> dechiffrer_fichier(cpri, "chiffre.png", "dechiffre.png")
 
Déchiffrement en cours...
50 ko - 100 ko - 150 ko - 200 ko - 250 ko -
Déchiffrement réalisé

39° Générer deux clés. Gardez les valeurs de la privées. Envoyer via l'ENT ou par mail la clé publique à vos destinataires.

40° Demander à cette personne de créer un fichier (texte, musique, pdf, video...) et de vous l'envoyer après l'avoir crypté avec la clé publique.

Il ne restera qu'à la décrypter avec la clé privée.

Attention : ça peut être long. C'est pour cela qu'on préférera utiliser un chiffrement symétrique une fois le canal sécurisé par le système asymétrique.

Enfin, le chiffrement et le déchiffrement sont moins gourmands en temps avec un système symétrique.

10 - FAQ

⇩ ⇧ ⤊

-

Petit théorème de Fermat (hors programme)

Enoncé

Si p est un nombre premier et
si a est un entier non divisible par p ,

alors a^p–1 – 1 est un multiple de p.

On pourrait donc écrire a^p–1 – 1 = k*p .

Ou on peut aussi écrire a^p–1 = k*p + 1 .

Or, le reste de la division de 1 par n'importe quel nombre donne bien un reste de 1. On peut donc écrire :

a^p–1 % p == 1 % p

Conséquence

Version 1 a^p–1 ≡ 1 (mod p)

Version 2 a^p ≡ a (mod p) (en multipliant par a de chaque côté)

Exemple

Prenons le nombre premier p = 17.

Prenons le nombre entier a = 50, non divisible par 17 : 50 / 17 =


>>> p = 17
>>> a = 50
 
>>> (a**(p-1)) % p == 1 % p
True
 
>>> (a**p) % p == a % p
True

Activité publiée le 16 02 2021
Dernière modification : 11 03 2021
Auteur : ows. h.

⏪

⏫

⏩