4 - Dépassement sur les entiers

⏪

⏬

⏩

1 - Dépass. capa +

2 - Dépass. capa -

3 - Log10

4 - Log2

5 - Multiplication

6 - Tronque addition

Nous avons vu une première fois le dépassement avec les entiers naturels.

Avec les entiers naturels, il y a dépassement dès qu'on tente d'affecter un bit qui sort de la zone réservée. C'est ainsi que sur un octet, un 255 se transforme en 0 lorsqu'on l'incrémente.

Nous allons voir que l'addition de deux nombres négatifs provoque nécessairement un dépassement de la zone mémoire mais pas un mauvais calcul puisqu'on ne tient pas compte du bit de dépassement.

Alors, comment savoir si un calcul est possible ou non ?

Cette activité est surtout une bonne excuse pour réviser l'encodage des entiers et les fonctions avant le DS !

Documents de cours : open document ou pdf

Logiciel nécessaire : Python ou Thonny, et le module Python matplotlib.

MODE COURS (cacher les questions)

1 - Addition et dépassement de capacité (cas positif)

⇩ ⇧ ⤊

Un dépassement de capacité est un dépassement des capacités de calculs corrects.

Dans le cas des entiers naturels, un dépassement caractérise toujours un dépassement des capacités de calcul : 255 + 1 donne 0 sur un octet !

Par contre, avec les entiers relatifs, il peut y avoir

dépassement sans dépassement des capacités de calculs
dépassement des capacités de calculs sans dépassement de la zone mémoire

Du coup, il va falloir être vigilant !

Addition de deux entiers positifs

Nous allons prendre le cas d'entiers signés sur un octet.

Exemple sans dépassement de capacité de calcul

Les bits codent		Sig.	64	32	16	8	4	2	1
+65		0	1	0	0	0	0	0	1
+33		0	0	1	0	0	0	0	1
(+65) + (+33) = +98	Ok	0	1	1	0	0	0	1	0

Exemple avec dépassement de capacité de calcul

Les bits codent		Sig.	64	32	16	8	4	2	1
+65		0	1	0	0	0	0	0	1
+66		0	1	0	0	0	0	1	0
(+65) + (+33) = +131 ?	Echec	1	0	0	0	0	0	1	1

On constate un grave problème : l'addition des bits de la représentation de deux nombres positifs donne un bit de signe à 1 ! L'ordinateur ne parvient donc pas à faire cette addition.

C'est normal : avec un entier signé sur un octet, on dispose de 7 bits pour la valeur. La valeur extrême positive est donc 2⁷ - 1, soit +127.

Comment détecter le dépassement de capacité de calcul lors de l'addition de deux entiers positifs ?

C'est "simple" : lorsqu'on additionne deux nombres positifs signés, il y a dépassement de capacité si le bit de signe change de valeur.

Si les deux nombres qu'on additionne ont un bit de signe à 0, on sait qu'on a un dépassement de capacité s'il passe à 1.

Si on cherche un test de vérification, on pourrait écrire

ENTREES : a et b, deux entiers positifs signés
On calcule et mémorise c = a + b
Si c est positif
- SORTIE : on renvoie True
Sinon

SORTIE : on renvoie False

01° On additionne un ensemble d'entiers positifs sur 8 ou 16 bits.

Sans même savoir quels sont les deux entiers positifs, donner les numéros des cas où il y a visiblement eu dépassement de capacités.

1 : 0101 0101 0101 0101
2 : 1101 0101
3 : 1111 1111 1111 1111
4 : 0000 0001
5 : 1000 0000

Correction ?

...CORRECTION...

Il suffit de chercher les résultats pour lesquels le bit de signe est devenu 1.

1 : 0101 0101 0101 0101 : ok
2 : 1101 0101 : dépassement
3 : 1111 1111 1111 1111 : dépassement
4 : 0000 0001 : ok
5 : 1000 0000 : dépassement

Reste à voir l'addition de deux valeurs négatives.

2 - Addition et dépassement de capacité (cas négatif)

⇩ ⇧ ⤊

Commençons par revoir comment obtenir deux nombres négatifs avec la méthode du complément à deux.

Commençons par un petit rappel sur le complément à deux

Exemple avec -6

Utilisons la méthode du complément à deux : on part de 6, on inverse et on rajoute de 1

Code	signe	64	32	16	8	4	2	1
Encodage de +6	0	0	0	0	0	1	1	0
Inversion	1	1	1	1	1	0	0	1
Rajout de 1	1	1	1	1	1	0	1	0

Comment obtenir le résultat plus rapidement ? On utilise un octet donc 8 bits. Il y a 256 cas possibles (2⁸). On obtient l'encodage de -6 en réalisant le complément à deux de 6 : 256 - 6 = 250, soit 1111 1010 .

Exemple avec -126

Cherchons l'encodage de -126 en partant de 126, en inversant et en rajoutant 1 :

Code	signe	64	32	16	8	4	2	1
Encodage de +126	0	1	1	1	1	1	1	0
Inversion	1	0	0	0	0	0	0	1
Rajout de 1	1	0	0	0	0	0	1	0

Comment obtenir le résultat plus rapidement ? On utilise un octet donc 8 bits. Il y a 256 cas possibles (2⁸). On obtient l'encodage de -6 en réalisant le complément à deux de 6 : 256 - 126 = 130, soit 1000 0010 .

Addition de deux entiers négatifs

Nous allons prendre le cas d'entiers signés sur un octet.

Exemple sans dépassement de capacité de calcul

-6		1	1	1	1	1	0	1	0
-6		1	1	1	1	1	0	1	0
Retenue	^⁺¹	^⁺¹	^⁺¹	^⁺¹	^⁺¹		^⁺¹
(-6) + (-6) = -12		1	1	1	1	0	1	0	0

On ne tient pas compte du dernier dépassement. Mais est-ce que cela donne bien -12 ?

Pour le savoir, il faut utiliser le complément à deux ! Soit avec la méthode de l'inversion et du plus 1 ou avec la méthode de 256 - la valeur de l'octet si c'était un entier naturel.

1er méthode

On part de 1111 0100

Inversion : 0000 1011

Rajout de 1 : 0000 1100

Lecture : 8+4 = 12. Il s'agit donc bien de l'encodage de -12.

2e méthode

On part de 1111 0100

Le contenu de l'octet lu comme un entier est 128+64+32+16+4 = 244.

On calcule 256 - 244 et on obtient bien 12.

Exemple avec dépassement de capacité de calcul

Les bits codent		Sig.	64	32	16	8	4	2	1
-6		1	1	1	1	1	0	1	0
-126		1	0	0	0	0	0	1	0
(-6) + (-126) = -132 ?	+1	0	1	1	1	1	1	0	0

On ne tient pas compte du dépassement avec cette méthode puisque l'addition de deux nombres négatifs provoque toujours un dépassement.

On constate un grave problème : l'addition des bits de la représentation de deux nombres négatifs donne un bit de signe à 0 ! L'ordinateur ne parvient donc pas à faire cette addition.

On retrouve le problème vu avec les nombres positifs.

Comment détecter le dépassement de capacité de calcul lors de l'addition de deux entiers négatifs ?

C'est "simple" : il y a dépassement de capacité si le bit de signe change de valeur.

Si on cherche un test de vérification, on pourrait écrire

ENTREES : a et b, deux entiers négatifs
On calcule et mémorise c = a + b
Si c est négatif
- SORTIE : on renvoie True
Sinon

SORTIE : on renvoie False

02° On additionne un ensemble d'entiers négatifs sur 8 ou 16 bits.

Sans même savoir quels sont les deux entiers positifs, donner les numéros des cas où il y a visiblement eu dépassement de capacités.

1 : 0101 0101 0101 0101
2 : 1101 0101
3 : 1111 1111 1111 1111
4 : 0000 0001
5 : 1000 0000

Correction ?

...CORRECTION...

Il suffit de chercher les résultats pour lesquels le bit de signe est devenu 0.

1 : 0101 0101 0101 0101 : dépassement
2 : 1101 0101 : ok
3 : 1111 1111 1111 1111 : ok
4 : 0000 0000 0000 0001 : dépassement
5 : 1000 0000 : ok

3 - Fonction logarithme base 10

⇩ ⇧ ⤊

Comment connaitre le nombre de chiffre nécessaire à l'écriture d'un nombre dans une base donnée ?

Pour cela, il suffit d'utiliser une fonction mathématique très connue et exploitée, la fonction logarithme.

Logarithme base 10

La fonction logarithme base 10 peut être vue en première approximation comme une fonction qui renvoie la puissance de 10 d'un nombre qu'on écrirait sous la forme N = 10 ^X.

Ainsi :

log₁₀(0,01) = log₁₀(10^-2) = -2

log₁₀(0,1) = log₁₀(10^-1) = -1

log₁₀(1) = log₁₀(10⁰) = 0

log₁₀(10) = log₁₀(10¹) = 1

log₁₀(100) = log₁₀(10²) = 2

La fonction logarithme est définie dans ℝ^*₊ , c'est à dire l'intervalle ] 0 ; +∞ ] .

On peut également rechercher des valeurs qui ne tombent pas juste. Par exemple pour 200 :

log₁₀(200) = 2.3010299956639813...

Cela veut néanmoins dire qu'on peut écrire approximativement

200 = 10^{2.3010299956639813...}

L'intérêt pour le traitement des nombres ? Cette fonction permet facilement de trouver le nombre de chiffres nécessaires pour écrire un nombre en base 10 !

Si on regarde bien :

1 + log₁₀(100) = 1 + log₁₀(10²) = 1 + 2 = 3

Le nombre 100₁₀ nécessite bien 3 chiffres en base 10.

On peut faire de même en ne prenant que la partie entière du résultat pour 200

1 + int(log₁₀(200)) = 1 + int(2.3010299956639813...) = 1 + 2 = 3 !

Ou même plus simplement

int(1 + log₁₀(200)) = int(1 + 2.3010299956639813...) = 3 !

A l'aide d'une simple formule, on parvient donc à trouver que 200₁₀ nécessite 3 chiffres pour s'écrire en base 10.

Voici donc à titre d'exemple une fonction Python utilisant le module math et permettant d'obtenir le nombre de chiffres nécessaires à l'écriture d'un nombre lorsqu'on l'écrit en base 10

# 1 - Importation des modules nécessaires
import math
 
# 2 - Déclaration des fonctions
 
def chiffres10(nombre):
    """Renvoie le nombre de chiffres nécessaires pour exprimer nombre en base 10
 
    ::param nombre (int/float) :: Un nombre > 0
    ::return (int) :: Le nombre de chiffres nécessaires en base 10
 
    """
    return int(1 + math.log10(nombre))

03° Placer le programme précédent en mémoire dans Thonny ou simplement IDLE Python.

Utiliser ensuite la console pour vérifier que la fonction fonctionne avec quelques exemples.

Vous devriez pouvoir obtenir des résultats de ce type

>>> chiffres_base10(200)
3
>>> chiffres_base10(2000)
4
>>> chiffres_base10(-2000)
    return 1 + int(math.log10(nombre))
ValueError: math domain error

04° Utiliser le code ci-dessous basé sur le module matplotlib. Il faudra peut-être l'importer dans Thonny. Visualiser les courbes obtenues en traçant la fonction log10 et le nombre de chiffres nécessaires.

Le code est fourni sans plus d'explications car une activité traitera du module matplotlib.

Pour importer un module dans Thonny, il faut aller dans le menu Tools - Manage Packages.

Si vous utilisez directement Python sans passer par Thonny, il est plus que propable que le module ne soit pas importé de base. Dans ce cas, ouvrir votre console Windows ou votre terminal Linux et taper ceci :


C:\Users\moi>python -m pip install --user matplotlib


rv@rv-HP2:~$ python3 -m pip install --user matplotlib

# 1 - Importation des modules nécessaires
import math
import matplotlib.pyplot as plt
 
# 2 - Variables globales
xmax = 150 # Valeur maximum du nombre à gérer
 
# 3 - Déclaration des fonctions
 
def chiffres_base10(nombre):
    """Renvoie le nombre de chiffres nécessaires pour exprimer nombre en base 10
 
    ::param nombre (int/float) :: Un nombre > 0
    ::return (int) :: Le nombre de chiffres nécessaires en base 10
 
    """
    return int(1 + math.log10(nombre))
 
# 4 - Programme principal
 
# Création des tableaux de données
abscisse = [ valeur/10 for valeur in range(1, xmax*10) ] # Entiers, la borne inférieure doit être >= 1
valeurs_log = [ math.log10(x) for x in abscisse ] # Ordonnée
nbr_chiffres = [ chiffres_base10(x) for x in abscisse ] # Ordonnée
ymax = max(nbr_chiffres) + 1
 
# Création des courbes
plt.plot(abscisse, valeurs_log, label="log10", color='orange')
plt.plot(abscisse, nbr_chiffres, label="Nbr chiffres", color="red")
plt.xlabel("Nombre")
plt.ylabel("Log10 et nbr de chiffres")
plt.title("Courbe du log10 pour en déduire le nombre de chiffres")
plt.legend(loc='upper center')
plt.axis([0, xmax, 0, ymax])
plt.grid()
plt.show() # Affichage à l'écran des courbes

Vous devriez obtenir une application graphique proche de ceci

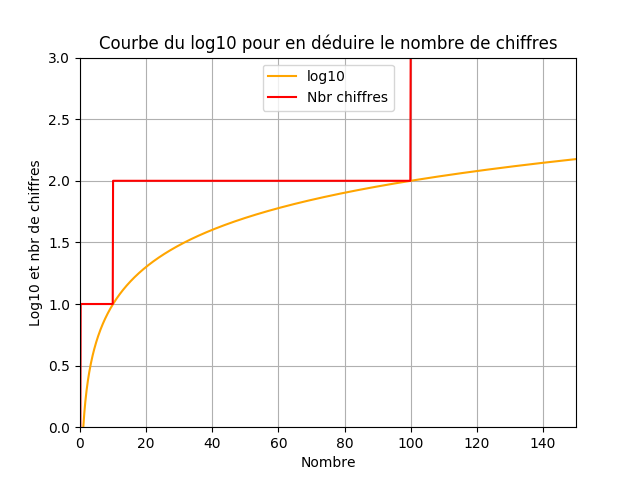
On constate bien qu'on a besoin

De 1 chiffre de 1 à 9
De 2 chiffres de 10 à 99
De 3 chiffres de 100 à 999
...

4 - Fonction logarithme base 2

⇩ ⇧ ⤊

Comment connaitre le nombre de chiffre nécessaire à l'écriture d'un nombre en base 2 ?

La solution : la fonction logarithme base 2 !

Logarithme base 2

La fonction logarithme base 2 peut être vue en première approximation comme une fonction qui renvoie la puissance de 2 d'un nombre qu'on écrirait sous la forme N = 2 ^X.

Ainsi :

log₂(0,25) = log₂(2^-2) = -2

log₂(0,5) = log₂(2^-1) = -1

log₂(1) = log₂(2⁰) = 0

log₂(2) = log₂(2¹) = 1

log₂(4) = log₂(2²) = 2

La fonction logarithme est définie dans ℝ^*₊ , c'est à dire l'intervalle ] 0 ; +∞ ] .

On peut également rechercher des valeurs qui ne tombent pas juste. Par exemple pour 6 :

log₂(6) = 2.584962500721156...

Cela veut néanmoins dire qu'on peut écrire approximativement

6 = 2^{2.584962500721156...}

L'intérêt pour le traitement des nombres ? Cette fonction permet facilement de trouver le nombre de chiffres nécessaires pour écrire un nombre en base 2 !

Si on regarde bien :

1 + log₂(4) = 1 + log₂(2²) = 1 + 2 = 3

Le nombre 4₁₀ nécessite bien 3 chiffres en base 2 : 100 ₂.

On peut faire de même en ne prenant que la partie entière du résultat pour 6

int(1 + log₂(6)) = int(1 + 2.584962500721156...) = int(3.584962500721156...) = 3 !

A l'aide d'une simple formule, on parvient donc à trouver que 6₁₀ nécessite 3 chiffres pour s'écrire en base 2 : 110

Le module math contient la fonction log2 qui permet de calculer le log en base 2 de l'argument fourni.

05° Compléter le code de la fonction ci-dessous. Pour l'instant, la fonction renvoie toujours 300.

# 1 - Importation des modules nécessaires
import math
 
# 2 - Déclaration des fonctions
 
def chiffres2(nombre):
    """Renvoie le nombre de chiffres nécessaires pour exprimer nombre en base 2
 
    ::param nombre (int/float) :: Un nombre > 0
    ::return (int) :: Le nombre de chiffres nécessaires en base 2
 
    """
    return 300

06° Utiliser le code ci-dessous basé sur le module matplotlib. Il faudra peut-être l'importer dans Thonny. Visualiser les courbes obtenues en traçant la fonction log2 et le nombre de chiffres nécessaires.

Le code est fourni sans plus d'explications car une activité traitera du module matplotlib.

# 1 - Importation des modules nécessaires
import math
import matplotlib.pyplot as plt
 
# 2 - Variables globales
xmax = 150 # Valeur maximum du nombre à gérer
 
# 3 - Déclaration des fonctions
 
def chiffres_base2(nombre):
    """Renvoie le nombre de chiffres nécessaires pour exprimer nombre en base 2
 
    ::param nombre (int/float) :: Un nombre > 0
    ::return (int) :: Le nombre de chiffres nécessaires en base 2
 
    """
    return int(1 + math.log2(nombre))
 
# 4 - Programme principal
 
# Création des tableaux de données
abscisse = [ valeur/10 for valeur in range(1, xmax*10) ] # Entiers, la borne inférieure doit être >= 1
valeurs_log = [ math.log2(x) for x in abscisse ] # Ordonnée
nbr_chiffres = [ chiffres_base2(x) for x in abscisse ] # Ordonnée
ymax = max(nbr_chiffres) + 1
 
# Création des courbes
plt.plot(abscisse, valeurs_log, label="log2", color='orange')
plt.plot(abscisse, nbr_chiffres, label="Nbr chiffres", color="red")
plt.xlabel("Nombre")
plt.ylabel("Log2 et nbr de chiffres")
plt.title("Courbe du log2 pour en déduire le nombre de chiffres")
plt.legend(loc='upper center')
plt.axis([0, xmax, 0, ymax])
plt.grid()
plt.show() # Affichage à l'écran des courbes

Vous devriez obtenir une application graphique proche de ceci

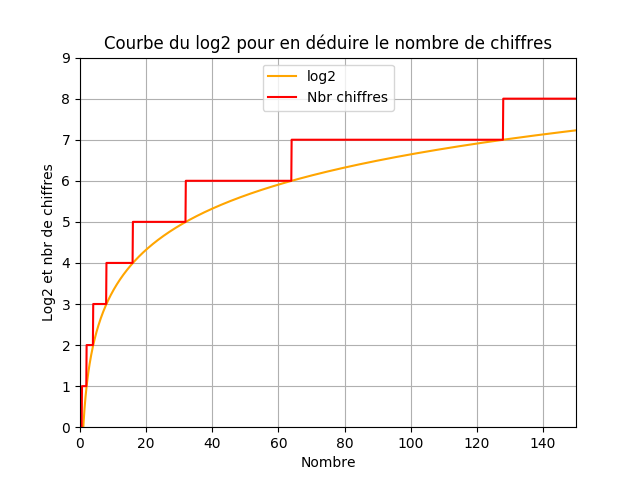
On constate bien qu'on a besoin

De 1 chiffre de 0 à 1
De 2 chiffres de 2 à 3
De 3 chiffres de 4 à 7
De 4 chiffres de 8 à 15
...

5 - Prévision des dépassements après multiplication

⇩ ⇧ ⤊

C'est maintenant que l'utilisation de la fonction logarithme prend tout son sens.

Nbr de bits THEORIQUEMENT nécessaires pour stocker a*b

La fonction logarithme possède la propriété suivante quelque soit la base utilisée :

log₂(a*b) = log₂(a) + log₂(b)

On constate donc que la multiplication se transforme en addition de log.

Lors d'une multiplication, nous aurons donc ceci

Pour le nombre a, le nombre N_a de bits est : N_a = int( 1 + log₂(a) )
Pour le nombre b, le nombre N_b de bits est : N_b = int( 1 + log₂(b) )
Pour le nombre a*b : N_a*b = int( 1 + log₂(a*b) ) = int( 1 + log₂(a) + log₂(b) ).

Si on considère le cas le plus favorable : N_a*b = N_a + N_b - 1

Si on considère le cas le plus défavorable : N_a*b = N_a + N_b

Bref, ce n'est pas si simple de prévoir à coup sur le nombre de bits qu'il faudra en connaissant juste le nombre de bits pour chacun des nombres de base...

Mais on peut faire plus simple !

Un moyen facile de vérifier si le résultat de la multiplication c = a * b est bon est de tester ceci pour b != 0 :

c / a == b

Si on cherche un test de vérification, on pourrait écrire

ENTREES : a et b, deux entiers, b étant non nul
On calcule et mémorise c = a * b
Si b == c // a
- SORTIE : on renvoie True
Sinon

SORTIE : on renvoie False

07° Combien faut-il de bits pour stocker la valeur a = 100 en base 2 ? Répondre en non signé et en signé.

Correction ?

...CORRECTION...

100₁₀ nécessite int(1 + math.log2(100)) chiffres en base 2.

Le calcul donne 7 chiffres.

C'est cohérent avec le fait que 2⁷ donne 128.

Recherche de la décomposition avec 1-2-4-8-16-32-64 qu'on utilisera dans le sens 64-32-16-8-4-2-1:

On active 64. Il 100-64 = 36.
On active donc 32. Il reste 36-32 = 4.
On active 4.

La décomposition de 100₁₀ sur 7 bits est donc 110 0100₂.

Pour un entier signé, il faudrait un bit supplémentaire pour le signe : 0110 0100 ₂

08° Combien faut-il de bits pour stocker la valeur b = 50 en base 2 ? Répondre en non signé et en signé.

Correction ?

...CORRECTION...

50₁₀ nécessite int(1 + math.log2(50)) chiffres en base 2.

Le calcul donne 6 chiffres.

C'est cohérent avec le fait que 2⁶ donne 64.

Recherche de la décomposition avec 1-2-4-8-16-32 qu'on utilisera dans le sens 32-16-8-4-2-1:

On active 32. Il 50-32 = 18.
On active donc 16. Il reste 18-16 = 2.
On active 2.

La décomposition de 50₁₀ sur 6 bits est donc 11 0010₂.

Pour un entier signé, il faudrait un bit supplémentaire pour le signe : 011 0010

09° Si on considère qu'il faut 7 bits pour stocker la valeur 100 et 6 bits pour stocker la valeur 50, la multiplication risque-t-elle de créer un problème de dépassement sur 16 bits dans le cas d'un entier non signé ? dans un entier signé ?

Correction ?

...CORRECTION...

Pour stocker 500 = 100 * 50, il prendra donc 7 + 6, soit 13 bits pour un entier non signé.

S'il s'agit d'entiers signés, il faudra 14 bits.

Dans les deux cas, utiliser un octet (8 bits) provoquera un débordement.

Dans les deux cas, utiliser deux octets (16 bits) permet d'obtenir le résultat sans problème.

10° On travaille avec des entiers naturels (non signés) encodés sur 2 octets. Peut-on calculer 30000 * 200 ?

Correction ?

...CORRECTION...

1er réponse rapide si on peut calculer le nombre : 30000*200 = 6 000 000.

Or avec 16 bits, on ne peut aller que jusqu'à 2¹⁶ -1 , soit 65535. La réponse est donc NON.

Si on ne peut pas calculer le résultat final ? Il suffit d'utiliser la formule.

L'encodage de 30000 nécessite 15 bits ( int(1 + math.log2(30000)) ou len(bin(30000)[2:]) ).

L'encodage de 200 nécessite 8 bits ( int(1 + math.log2(200)) ou len(bin(200)[2:]) ).

Stocker le résultat demande en gros 23 bits (15+8).

Voir 24 bits s'il s'agit d'entiers signés.

Sur 2 octets (16 bits), il y aura donc débordement de capacité.

Par contre, sur 4 octets (32 bits), le calcul ne posera pas problème.

Comme Python ne vous permet pas de gérer la taille de vos entiers, voici une courte fonction qui permet de simuler cela (en utilisant la manipulation des strings et les fonctions bin et int).

def tronque(nombre, nombre_bits):
    """Renvoie l'entier non signé décodé lorsqu'on ne gère qu'un nombre limité de bits
 
    ::param nombre(int) :: un entier > 0
    ::param nombre_bits (int) :: un entier > 0
    ::return (int) :: le résultat tronqué par le nombre de bits disponibles
 
    """
    bits = bin(nombre)
    bits = bits[2:] # Permet de supprimer le 0b du début
    if len(bits) > nombre_bits :
        calcul = '0b' + bits[-nombre_bits:] # On ne prend que qqs bits depuis la droite
        return int(calcul,2)
    else :
        return nombre

11° Mémoriser la fonction dans Thonny ou IDLE. Lancer les calculs suivants dans la console :


>>> tronque(10*10,8)
>>> tronque(100*10,8)

Vérification PRATIQUE de non dépassement en cas de multiplication

Dans le cas d'entiers signés de même signe, on peut affirmer qu'il y a dépassement si l'entier obtenu n'a pas le même signe.

Dans le cas d'entiers non signés, on peut vérifier le non-dépassement éventuel de c = a * b en vérifiant que a = c // b . Si on n'obtient pas le bon résultat, c'est que l'opération a provoqué un dépassement.

6 - Tronque et addition

⇩ ⇧ ⤊

Détection de dépassement par addition

La détection a déjà été vue dans le cas de nombres signés : il y a débordement si l'addition de deux nombres de même signe donnent un entier de signe différent.

L'addition de deux nombres de signes différents ne peut pas donner lieu à de dépassement du fait du mécanisme du complément à deux.

Dans le cas d'entiers non signés, on peut voir l'existence d'un dépassement si a+b est inférieur à a !

12° Mémoriser la fonction dans Thonny ou IDLE. Lancer les calculs suivants dans la console :


>>> tronque(250+100,16)
>>> tronque(250+100,8)

Bien entendu, en Python ces vérifications sont inutiles puisque l'interpréteur se charge de tout. Mais avec d'autres langages, il va falloir mettre des fonctions de vérifications au point si vous voulez éviter les dysfonctionnements !

Activité publiée le 22 10 2019
Dernière modification : 25 10 2019
Auteur : ows. h.

⏪

⏫

⏩