4 - Encodage des grands entiers naturels

⏪

⏬

⏩

1 - entiers naturels

2 - plusieurs octets

3 - Dépassement

4 - FAQ

Nous avons vu comment stoker un entier naturel dont la valeur est comprise entre 0 et 255.

Oui, mais... Comment stocker un entier valant plus que 255 ?

Documents de cours : open document ou pdf

Exercices corrigés complémentaires de cours : exos

MODE COURS (cacher les questions)

1 - Entiers naturels

⇩ ⇧ ⤊

1.1 Encodage des entiers naturels : unsigned integers

Voir

Les entiers naturels sont les entiers positifs.

Ils appartiennent à l'ensemble noté ℕ.

On les encode en utilisant un certain nombre de bits dont le poids est 1, 2, 4, 8...

Dans la plupart des langages, cet encodage est nommé unsigned : le nombre n'est pas signé, on ne peut pas représenter de nombre négatif.

Pour rappel, voici des exemples sur un octet (8 bits) :

Votre nombre binaire M :

Nombre M =
Les bits codent	128	64	32	16	8	4	2	1
On obtient donc

D'où la valeur de M en base 10 : M = = .

Avec un octet, on dispose de x = 8 bits.

Valeur minimale : 0
Valeur maximale : 2⁸-1, donc 255.

Avec deux octets, on dispose de x = 16 bits.

Valeur minimale : 0
Valeur maximale : 2¹⁶-1, donc 65 535.

Avec quatre octets, on dispose de x = 32 bits.

Valeur minimale : 0
Valeur maximale : 2³²-1, donc 4 294 967 295.

Conclusion : plus on a d'octets, plus on peut encoder de grands nombres.

Dans cette partie, nous allons voir quelques fonctions Python qui vont nous permettre de travailler facilement sur ces représentations binaires.

01° Utiliser le convertisseur contenu dans la partie de cours ci-dessus pour répondre aux questions suivantes :

Quelle est la valeur du plus grand entier naturel encodable avec 8 bits (tous les bits sont à 1) : 1111 1111 ₂.
Quelle formule permet de connaître la valeur maximale encodable par 8 bits ?
Donner la valeur en base 10 de 0000 1111 ₂
Donner la valeur en base 10 de 0000 1001 ₂.

Correction ?

...CORRECTION...

On peut voir que (1111 1111)₂ = (255)₁₀

La formule permettant de retrouver cette valeur est 2⁸ - 1.

0000 1111 ₂ = (8+4+2+1) ₁₀ = 15 ₁₀, qu'on notera juste 15.

0000 1001 ₂ = (8+1) ₁₀ = 9 ₁₀, qu'on notera juste 9.

Si on veut encoder des valeurs supérieures à 255, il suffit donc de rajouter des bits supplémentaires à gauche. Ces bits pèseront donc

2⁸, c'est à dire 256
2⁹, c'est à dire 512
2¹⁰, c'est à dire 1024
...

02° Quels sont les entiers naturels encodables avec les deux suites de 9 bits suivantes :

1 0000 0000
1 0000 0001

Correction ?

...CORRECTION...

Premier cas : seul le bit de poids fort est activé. Le nombre vaut donc 256₁₀.

Nombre M =	1	0	0	0	0	0	0	0	0
Les bits codent	256	128	64	32	16	8	4	2	1
On obtient donc	256

Deuxième cas : seuls les bits de poids faible et de poids fort sont activés.

Comme nous avons 9 bits, il s'agit des bits de poids 256 et 1.

Nombre M =	1	0	0	0	0	0	0	0	0
Les bits codent	256	128	64	32	16	8	4	2	1
On obtient donc	256								1

On encode donc le nombre 256 + 1, soit 257₁₀.

Vérifions cela avec Python :

1.2 Décimal vers binaire avec bin()

Voir

Description

La fonction native bin() a besoin d'un paramètre de type integer contenant le nombre à traiter et renvoie un string contenant la représentation binaire.

bin(number:int) -> str


>>> bin(255)
'0b11111111'

Python précise avec 0b que ce string est une représentation d'un encodage binaire.

Enlever 0b

Pour obtenir une copie sans les 2 premiers caractères d'un string, on peut rajouter [2:] derrière le nom du string.

L'interpréteur Python comprend que vous ne voulez que les indices 2 et plus.


>>> bin(255)[2:]
'11111111'
 
>>> bin(255)
'0b11111111'


>>> bin(256)[2:]
'100000000'
 
>>> bin(257)[2:]
'100000001'

On voit qu'il faut 9 bits pour encoder 256 ou 257.

Obtenir le nombre de bits nécessaires

On utilise la fonction native len() sur la réponse tronquée des deux premiers caractères de bin().

En deux lignes :


>>> s = bin(257)[2:]
>>> len(s)
9

En une ligne :


>>> len(bin(257)[2:])
9

03° Lancer les instructions suivantes dans une console Python :


>>> bin(255)
'0b11111111'
 
>>> bin(256)
'0b100000000'
 
>>> bin(257)
'0b100000001'

Question

Qu'est-ce qui indique clairement que la réponse de la fonction native bin() est de type string ?
Dans cette réponse, qu'est-ce qui indique qu'il s'agit d'un contenu affiché en binaire ?

Correction ?

...CORRECTION...

La présence de guillemets simples autour de la réponse permet de voir qu'il s'agit d'un string.


>>> bin(255)
'0b11111111'

Ce string contient les valeurs des différents bits. On le différencie des autres strings par le fait qu'il commence par 0b.


>>> bin(255)
'0b11111111'

On peut également travailler dans l'autre sens : fournir un nombre sous forme binaire et voir sa valeur en décimal.

1.3 Binaire vers décimal

Voir

On peut fournir un entier naturel sous forme binaire en transmettant la valeur binaire précédée du suffixe 0b.


>>> nombre = 0b11
>>> nombre
3

04° Utiliser le code ci-dessous qui enregistre une valeur sous forme binaire dans une variable nombre. On affiche ensuite le contenu.


>>> nombre = 0b100000001
>>> nombre
257

Comme vous pouvez le voir, Python est configuré pour afficher les nombres en base 10 quelque soit la façon dont ils ont été fournis.

Pour obtenir un nombre si on dispose d'un string ? Il suffit d'utiliser la fonction native int() qui tente de convertir le contenu que vous allez lui fournir en integer, en entier.

05° Utiliser le code suivant qui vous montre plusieurs tentatives possibles de conversion en entier. Comme vous pouvez le voir, si on fournit un string, il faut indiquer à l'interpréteur la base avec laquelle décoder.

Nous avons déjà rencontré la fonction native int(), elle permet notamment de convertir une entrée clavier en integer. On lui transmet parfois un deuxième argument : 2, pour indiquer qu'elle doit tenter de décoder ce qu'on lui donne comme un nombre en binaire, la base 2.


>>> int('0b11', 2)
3
 
>>> int('11', 2)
3

2 - Plusieurs octets

⇩ ⇧ ⤊

Alors, comment décoder une série de 4 octets A B C D ?

Par exemple :

A = 0000 0001 ₂
B = 0000 0010 ₂
C = 0000 0011 ₂
D = 0000 0100 ₂

En mémoire, nous avons donc la suite de bits suivante :

0000 0001 0000 0010 0000 0011 0000 0100

Cas de l'encodage sur un seul octet

Explications (lecture directe 0 à 255)

Voir

Un seul octet, on fait donc des paquets de 8 bits.

Les nombres sont

N₁ = A = 0000 0001 ₂ = 1 en décimal
N₂ = B = 0000 0010 ₂ = 2 en décimal
N₃ = C = 0000 0011 ₂ = 3 en décimal
N₄ = D = 0000 0100 ₂ = 4 en décimal

Facile.

Cas de l'encodage sur deux octets

Explications version 1 : lecture directe 0 à 65535

Voir

Deux octets, on fait donc des paquets de 16 bits.

Les nombres sont encodés par la concaténation des octets A B et la concaténation des octets C D.

N₁ = A B = 0000 0001 0000 0010 ₂ = 258 en décimal
N₂ = C D = 0000 0011 0000 0100 ₂ = 772 en décimal

Voyons pourquoi.

Voici le poids des bits de la suite A B des 16 bits suivants : 0000 0001 0000 0010 :

N₁ =	0	0	0	0	0	0	0	1	0	0	0	0	0	0	1	0
Poids	32768	16384	8192	4096	2048	1024	512	256	128	64	32	16	8	4	2	1

On obtient donc N₁ = 256 + 2 = 258.

Voici le poids des bits de la suite C D des 16 bits suivants : 0000 0011 0000 0100 :

N₂ =	0	0	0	0	0	0	1	1	0	0	0	0	0	1	0	0
Poids	32768	16384	8192	4096	2048	1024	512	256	128	64	32	16	8	4	2	1

On obtient donc N₂ = 512 + 256 + 4 = 772.

C'est facile à comprendre, mais long à décoder puisqu'il faut rechercher le poids de toutes les cases.

Explications version 2 : lecture indirecte via deux octets 0 à 255

Voir

Voyons comment faire plus rapide avec les puissances de 2 :

Prérequis

Il suffit d'utiliser quelques formules sur les exposants et les fonctions exponentielles :

2^a+b = 2^a * 2^b

Quelques exemples pour montrer que cela fonctionne :

2⁶ = 2⁴ * 2² = 16 * 4 = 64
2⁸ = 2⁸ * 2⁰ = 256 * 1 = 256
2⁹ = 2⁸ * 2¹ = 256 * 2 = 512
2¹⁰ = 2⁸ * 2² = 256 * 4 = 1024
...

Principe d'un encodage sur deux octets

L'idée est donc d'écrire :

les poids des 8 bits de gauche sous la forme 256 * 2^X ou 2⁸ * 2^X
les poids des 8 bits de droite sous la forme 1 * 2^X.

Nombre N₁ =	0	0	0	0	0	0	0	1	0	0	0	0	0	0	1	0
Poids	2¹⁵ = 2⁸ * 2⁷	2¹⁴ = 2⁸ * 2⁶	2¹³ = 2⁸ * 2⁵	2¹² = 2⁸ * 2⁴	2¹¹ = 2⁸ * 2³	2¹⁰ = 2⁸ * 2²	2⁹ = 2⁸ * 2¹	2⁸ = 2⁸ * 2⁰	2⁷ = 1 * 2⁷	2⁶ = 1 * 2⁶	2⁵ = 1 * 2⁵	2⁴ = 1 * 2⁴	2³ = 1 * 2³	2² = 1 * 2²	2¹ = 1 * 2¹	2⁰ = 1 * 2⁰
On obtient donc	Octet de poids fort Y = 0000 0001 = 1 mais sa case pèse 2⁸								Octet de poids faible Z = 0000 0010 = 2 mais sa case pèse 1

Avec cette façon de faire, on obtient donc :

N₁ = 256 * Y + 1 * Z

N₁ = 256 * 1 + 1 * 2

N₁ = 256 + 2

N₁ = 258

Conclusion

On voit qu'on peut simplifier la lecture des 16 bits en les séparant en deux lectures de 8 bits Y et Z. Il suffit de multiplier le premier octet Y par 256 et Z par 1.

Si on résume ceci par un graphe :

2.1 Encodage d'un entier non signé sur 2 octets

Voir

A - Lecture directe des 16 bits

Avec une séquence de 2 octets, on dispose de 16 bits.

Le nombre de cas est 2¹⁶, soit 65536.
Les 16 bits à 0 - La plus petite valeur est 0
Les 16 bits à 1 - La plus grande valeur est 2¹⁶-1, soit 65535

On peut donc représenter des nombres variant de 0 à 65535.

Pour obtenir la valeur, il suffit de faire la somme des bits activés. Facile, mais long.

B - Lecture indirecte de 2 octets

Soit un nombre N encodé comme une suite de deux octets N = Y Z .

On lit Y comme un nombre entre 0 et 255.
On lit Z comme un nombre entre 0 et 255.

On obtient la valeur de N en base 10 en calculant :

N = Y * 256 + Z.

On peut bien entendu écrire cela avec les puissances de 2, ce qui permet de voir que les octets de Y sont en réalité à décaler de 8 cases et que les octets de Z n'ont pas à être décalés.

N = Y * 2⁸ + Z * 2⁰

C - Remarque : base 256 ?

On travaille ici presque en base 256 :

chaque case (Y et Z) contient un nombre compris entre 0 et 255
chaque case possède un poids lié à une puissance de 256 : 256⁰ pour Z, 256¹ pour Y.
La seule différence avec une "vraie" base 256 : on ne dispose pas des 256 symboles de chiffres, mais on pourrait.

D - Exemple sous forme de graphe

Une remarque en passant : Encodage Base 64

On peut recevoir des pièces jointes directement encodées sous forme de suite de caractères avec la base 64.

Notation du contenu en bits d'un octet

Donner les bits un par un, c'est un peu long.

S = 0000 0101

Dans la suite de ce cours, nous allons souvent donner le contenu d'un octet sans donner directement ses bits.

Pour décrire les bits d'un octet, on peut donner l'entier naturel que ces bits pourraient encoder.

Ainsi, plutôt que de noter S = 0000 0101 , on peut noter S = 5 pour indiquer que les bits de S sont 0000 0101 .

06° En considérant un encodage sur 2 octets d'entiers naturels, déterminer les entiers N_A et N_B décodables à partir des suites de bits suivantes :

Nombre N_A : 6 4 ( ou en version binaire 0000 0110 0000 0100 )
Nombre N_B : 3 4 ( ou en version binaire 0000 0011 0000 0100 )

Correction ?

...CORRECTION...

Nombre N_A = 6 * 256 + 4 = 1540
Nombre N_B = 3 * 256 + 4 = 772

07° En considérant un encodage sur 2 octets d'entiers naturels, déterminer les entiers N_C et N_D décodables à partir des suites de bits suivantes :

Nombre N_C : 5 130 ( ou en version binaire 0000 0101 1000 0010 )
Nombre N_D : 130 5 ( ou en version binaire 1000 0010 0000 0101 )

Question supplémentaire : l'ordre des octets reçus a-t-il un impact sur le nombre décodé ?

Correction ?

...CORRECTION...

Nombre N_C = 5 * 256 + 130 = 1410
Nombre N_D = 130 * 256 + 5 = 33285

On voit donc bien que l'ordre des octets est important. On ne donne pas le même sens à 5 130 et à 130 5 .

08° En considérant un encodage sur 2 octets d'entiers naturels, déterminer les entiers N_E et N_F décodables à partir des suites de bits suivantes :

Nombre N_E : 0 65 ( ou en version binaire 0000 0000 0100 0001 )
Nombre N_F : 65 0 ( ou en version binaire 0100 0001 0000 0000 )

Question supplémentaire : si on veut exprimer l'entier 10 en l'encodant avec deux octets, l'octet ne comportant que des 0 doit-il être à gauche ou à droite ? Ecrire la suite de 16 bits obtenue.

Correction ?

...CORRECTION...

Nombre N_E = 0 * 256 + 65 = 65
Nombre N_F = 65 * 256 + 0 = 16640

Si on veut écrire 10 sur deux octets, on écrit donc 0 10 pour que le deuxième octet compte bien juste pour 10 : 0*256 + 10*1.

La suite de bits est donc : 0000 0000 0000 1010

Cas de l'encodage sur quatre octets

Sur 4 octets, c'est donc toujours une sorte de base 256 avec plus de cases. Regardons.

2.2 Encodage d'un entier non signé sur 4 octets

Voir

A - Lecture directe des 32 bits

Avec une séquence de 4 octets, on dispose de 32 bits.

Le nombre de cas est 2³², soit 4 294 967 296, un peu plus de 4 milliards.
Les 32 bits à 0 - La plus petite valeur est 0
Les 32 bits à 1 - La plus grande valeur est 2³²-1, soit 4 294 967 295

On peut donc représenter des nombres variant de 0 à 4 294 967 295.

Pour obtenir la valeur, il suffit de faire la somme des bits activés. Facile, mais très long.

B - Lecture indirecte de 4 octets

Soit un nombre N encodé comme une suite de quatre octets N = W X Y Z .

On lit W comme un nombre entre 0 et 255.
On lit X comme un nombre entre 0 et 255.
On lit Y comme un nombre entre 0 et 255.
On lit Z comme un nombre entre 0 et 255.

On obtient la valeur de N en base 10 en calculant :

N = W * 16777216 + X * 65536 + Y * 256 + Z

On peut bien entendu écrire cela avec les puissances de 2, ce qui permet de voir que les octets de W sont en réalité à décaler de 24 cases, ceux de X de 16 cases...

N = W * 2²⁴ + X * 2¹⁶ + Y * 2⁸ + Z

On peut le comprendre en l'exprimant en respectant la notion de base 256 :

Poids des cases exprimés de trois façons différentes mais pour un résultat similaire :

Nombre N =	W	X	Y	Z
Le poids de cette case est	2²⁴	2¹⁶	2⁸	2⁰
Le poids de cette case est	16777216	65536	256	1
Le poids de cette case est	256³	256²	256¹	256⁰

N = W * 256³ + X * 256² + Y * 256¹ + Z

D - Exemple sous forme de graphe

09° En considérant un entier naturel N_G encodé sur 4 octets, déterminer sa valeur à l'aide de la suite d'octets suivante :

N_G : 1 2 3 4

Pour information, cela donne la suite de bits suivante en mémoire :

0000 0001 0000 0010 0000 0011 0000 0100

Correction ?

...CORRECTION...

Il suffit de réaliser le calcul suivant :

N_G = 1*256**3 + 2*256**2 + 3*256**1 + 4

N_G = 16 909 060

Vous auriez pu également passer par les puissances de 2.

N_G = 1*2**24 + 2*2**16 + 3*2**8 + 4

10° En considérant un entier naturel N_H encodé sur 4 octets, déterminer la valeur encodée par la suite d'octets suivante :

N_H : 10 20 255 0

Correction ?

...CORRECTION...

Il suffit de réaliser le calcul suivant :

N_H = 10*256**3 + 20*256**2 + 255*256**1 + 0

N_H = 169 148 160

11° En considérant un entier naturel N_I encodé sur 4 octets, déterminer la valeur encodée par la suite d'octets suivante :

N_I : 255 255 255 255

Question supplémentaire : comparer votre résultat à 2³²-1. Justifiez l'égalité.

Correction ?

...CORRECTION...

Il suffit de réaliser le calcul suivant :

N_I = 255*256**3 + 255*256**2 + 255*256**1 + 255

N_I= 4 294 967 295

Nous venons de remplir tous les octets. Cela forme donc une suite de 32 bits. Or, la valeur maximale encodable avec 32 bits est 2³²-1.

12° Combien d'octets faut-il pour encoder un entier naturel valant 6 milliards :

1 octet
2 octets
4 octets
8 octets

Correction ?

...CORRECTION...

Nous venons de voir qu'avec 4 octets, on peut encoder un peu plus de 4 milliards.

Pour 6 milliards, il faudra donc 8 octets, 4 ou moins est insuffisant.

2.3 Tableau et largeur des cases

Voir

Dans un tableau, toutes les cases doivent contenir le même nombre d’octets. C'est à dire que si vous voulez que l'une des cases contienne 600 (2 octets nécessaires) même si toutes les autres sont inférieures à 255 (1 octet est suffisant), il faudra que toutes les cases soient de deux octets.

Ainsi, il faudra encoder

0 par 0000 0000 0000 0000 .
1 par 0000 0001 0000 0000 .
2 par 0000 0010 0000 0000 .
...

Cela va perdre de la place mémoire mais nous verrons que cela permet d'accéder à n'importe quelle case du tableau très rapidement.

13° Quelle place mémoire doit-on réserver si on veut créer un tableau de 100 cases pouvant contenir des valeurs allant jusqu'à 200 ?

Correction ?

...CORRECTION...

Un octet suffit pour chaque case (avec un octet, on peut encoder des valeurs entre 0 et 255).

Il faut 100 cases donc 100 octets.

14° Quelle place mémoire doit-on réserver si on veut créer un tableau de 100 cases pouvant contenir des valeurs allant jusqu'à 65535 ?

Correction ?

...CORRECTION...

65535 est la valeur maximale encodable avec deux octets.

Il faut 100 cases donc 100*2 = 200 octets.

15° Quelle place mémoire doit-on réserver si on veut créer un tableau de 100 cases pouvant contenir des valeurs allant jusqu'à 4 milliards ?

Correction ?

...CORRECTION...

Nous avons vu qu'avec 4 octets, on peut encoder une valeur maximale un peu plus grande que 4 milliards.

Il faut 100 cases donc 100*4 = 400 octets.

3 - Dépassement

⇩ ⇧ ⤊

Le problème du dépassement de zone mémoire allouée

A partir du moment où on a demandé une place mémoire pour stocker notre entier, l'ordinateur va donc réserver cette place. Par exemple deux octets.

Mais il fait attention à un cas de figure particulier : on additionne deux entiers de 2 octets chacun mais le résultat final ne tient pas sur deux octets : il en faudrait au moins un troisième.

Par exemple :

65534 tient bien sur 2 octets (c'est bien un nombre entre 0 et 65535)

1111 1111 1111 1110

100 tient bien sur 2 octets (c'est bien un nombre entre 0 et 65535)

0000 0000 0110 0100

Mais 65534 + 100 vaut 65634. Et c'est supérieur à 65535 ! Il faudrait donc plus de 2 octets pour le stocker.

1 0000 0000 0110 0010

3.1 Addition de deux nombres binaires, bit à bit

Voir

Rappel des additions en binaire

0 + 0 = 0 qu'on écrirait en décimal 0+0 = 0
0 + 1 = 1 qu'on écrirait en décimal 0+1 = 1
1 + 0 = 1 qu'on écrirait en décimal 1+0 = 1
1 + 1 = 10 qu'on écrirait en décimal 1+1 = 2
1 + 1 + 1 = 11 qu'on écrirait en décimal 1+1+1 = 3

Principe de l'addition colonne par colonne

Nous avons vu comment incrémenter de 1 un nombre dans l'activité précédente : on additionne notre nombre et un autre nombre ne comportant qu'un bit activé celui du bit de poids faible.

Avec deux nombres différents de 1, c'est pareil, si ce n'est qu'on travaille sur tous les bits à la fois. Il est donc possible d'avoir deux 1 et une retenu +1 issue de la case de droite. D'où le cas 1+1+1.

Exemple (animation)

Addition N = A+B — CLIQUER SUR L'IMAGE pour ANIMER ou STOPPER

On remarquera que calculer en base 2 ou en base 10 ne change rien au résultat.


>>> 0b0101010101010101
21845
 
>>> 0b0100100100100100
18724
 
>>>bin(0b0101010101010101 + 0b0100100100100100)
'0b1001111001111001'
 
>>> 0b1001111001111001
40569
 
>>> 21845+18724
40569

Même exemple mais en pas à pas

voir ?

...exemple pas à pas...

Nombre A	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
Nombre B	0	1	0	0	1	0	0	1	0	0	1	0	0	1	0	0
Retenue ?
N = A + B																1

Nombre A	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
Nombre B	0	1	0	0	1	0	0	1	0	0	1	0	0	1	0	0
Retenue ?
N = A + B															0	1

Nombre A	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
Nombre B	0	1	0	0	1	0	0	1	0	0	1	0	0	1	0	0
Retenue ?													^⁺¹
N = A + B														0	0	1

Nombre A	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
Nombre B	0	1	0	0	1	0	0	1	0	0	1	0	0	1	0	0
Retenue ?													^⁺¹
N = A + B													1	0	0	1

Nombre A	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
Nombre B	0	1	0	0	1	0	0	1	0	0	1	0	0	1	0	0
Retenue ?													^⁺¹
N = A + B												1	1	0	0	1

Nombre A	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
Nombre B	0	1	0	0	1	0	0	1	0	0	1	0	0	1	0	0
Retenue ?													^⁺¹
N = A + B											1	1	1	0	0	1

Nombre A	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
Nombre B	0	1	0	0	1	0	0	1	0	0	1	0	0	1	0	0
Retenue ?													^⁺¹
N = A + B										1	1	1	1	0	0	1

Nombre A	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
Nombre B	0	1	0	0	1	0	0	1	0	0	1	0	0	1	0	0
Retenue ?													^⁺¹
N = A + B									0	1	1	1	1	0	0	1

Nombre A	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
Nombre B	0	1	0	0	1	0	0	1	0	0	1	0	0	1	0	0
Retenue ?							^⁺¹						^⁺¹
N = A + B								0	0	1	1	1	1	0	0	1

Nombre A	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
Nombre B	0	1	0	0	1	0	0	1	0	0	1	0	0	1	0	0
Retenue ?							^⁺¹						^⁺¹
N = A + B							1	0	0	1	1	1	1	0	0	1

Nombre A	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
Nombre B	0	1	0	0	1	0	0	1	0	0	1	0	0	1	0	0
Retenue ?							^⁺¹						^⁺¹
N = A + B						1	1	0	0	1	1	1	1	0	0	1

Nombre A	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
Nombre B	0	1	0	0	1	0	0	1	0	0	1	0	0	1	0	0
Retenue ?							^⁺¹						^⁺¹
N = A + B					1	1	1	0	0	1	1	1	1	0	0	1

Nombre A	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
Nombre B	0	1	0	0	1	0	0	1	0	0	1	0	0	1	0	0
Retenue ?							^⁺¹						^⁺¹
N = A + B				1	1	1	1	0	0	1	1	1	1	0	0	1

Nombre A	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
Nombre B	0	1	0	0	1	0	0	1	0	0	1	0	0	1	0	0
Retenue ?							^⁺¹						^⁺¹
N = A + B			0	1	1	1	1	0	0	1	1	1	1	0	0	1

Nombre A	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
Nombre B	0	1	0	0	1	0	0	1	0	0	1	0	0	1	0	0
Retenue ?	^⁺¹						^⁺¹						^⁺¹
N = A + B		0	0	1	1	1	1	0	0	1	1	1	1	0	0	1

Au final

Nombre A	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
Nombre B	0	1	0	0	1	0	0	1	0	0	1	0	0	1	0	0
Retenue ?	^⁺¹						^⁺¹						^⁺¹
N = A + B	1	0	0	1	1	1	1	0	0	1	1	1	1	0	0	1

16° Réaliser l'addition suivante sur votre copie. Le contenu du tableau est éditable.

Nombre A	0	1	0	1	0	1	0	1	0	1	0	1	0	1	1	1
Nombre B	0	1	0	0	1	0	0	1	0	0	1	0	0	1	1	0
Retenue ?
N = A + B

Correction ?

...CORRECTION...

Nombre A	0	1	0	1	0	1	0	1	0	1	0	1	0	1	1	1
Nombre B	0	1	0	0	1	0	0	1	0	0	1	0	0	1	1	0
Retenue ?	^⁺¹						^⁺¹						^⁺¹	^⁺¹
N = A + B	1	0	0	1	1	1	1	0	0	1	1	1	1	1	0	1

17° Réaliser l'addition suivante sur votre copie. Le contenu du tableau est éditable.

Quel est le problème ?

Nombre A	1	1	0	1	0	1	0	1	0	1	0	1	0	1	1	1
Nombre B	0	1	0	0	1	0	0	1	0	0	1	0	0	1	1	0
Retenue ?
N = A + B

Correction ?

...CORRECTION...

Nombre A	1	1	0	1	0	1	0	1	0	1	0	1	0	1	1	1
Nombre B	0	1	0	0	1	0	0	1	0	0	1	0	0	1	1	0
Retenue ?	^⁺¹						^⁺¹						^⁺¹	^⁺¹
1	0	0	0	1	1	1	1	0	0	1	1	1	1	1	0	1

Le problème est donc qu'on écrit en dehors de notre zone de 16 bits. On pourrait écraser le contenu du bit situé à gauche. Or ce contenu est peut être utilisé pour encoder quelque chose d'autre et n'a rien demandé à personne. Il s'agit d'un dépassement.


     11010101 01010111  
 +   01001001 00100110
 --------------------- 
 = 1 00011110 01111101

Et même si on n'écrase rien et qu'on garde uniquement le bon nombre d'octets, on obtient ainsi un retour à 0.

3.2 Dépassement

Voir

Principe

On parle de dépassement lorsque la somme réelle devrait donner un résultat supérieur à la valeur maximale encodable avec ce nombre d'octets.

Exemple 1 (sur un octet)

C'est ce qui s'est passé avec notre robot fou de l'activité précédente.


     11111111  (A = 255)
 +          1  (B = 1)
 ------------ 
 = 1 00000000  (C = A + B = 0 sur deux octets !)

Exemple 2 (sur un octet)

Un entier A sur un octet contient 250. Un autre entier B contient 10. La somme de A + B provoquerait un dépassement puisqu'on ne peut pas stocker 260 sur un seul octet !


     11111010  (A = 250) 
 +   00001010  (B = 10)
 ------------ 
 = 1 00000100  (C = A + B = 4 sur deux octets!)

Exemple 3 (sur deux octets)

On encode le nombre A = 16384 sur deux octets : 64 0

En effet, on peut obtenir 16384 en calculant 64 * 256 + 0.

La suite des 16 bits donne donc 01000000 00000000

On encode le nombre B = 49152 sur deux octets : 192 0

En effet, on peut obtenir 49152 en calculant 192 * 256 + 0.

La suite des 16 bits donne donc 11000000 00000000

Si on calcule de tête A + B = 16384 + 49152, cela donne 65536. Cela veut dire qu'un système traitant les entiers sur 2 octets ne parviendra pas à obtenir le bon résultat : avec deux octets, on ne peut travailler correctement que jusqu'à 65535 !


     01000000 00000000  (A = 16384)
 +   11000000 00000000  (B = 49152)
 --------------------- 
 = 1 00000000 00000000  (C = A + B = 0 sur deux octets !)

A cause du dépassement du résultat sur 2 octets, le système informatique dira donc que 16384 + 49152 = 0 !

Exemple 4 (sur deux octets)

Sur 2 octets, 16384 + 49154 = 2.


     01000000 00000000  (A = 16384)
 +   11000000 00000010  (B = 49154)
 --------------------- 
 = 1 00000000 00000010  (C = A + B = 2 sur deux octets !)

3.3 Dépassement avec Python ?

Voir

Python est un langage qui gère la taille nécessaire pour l'utilisateur. S'il faut 8 octets, il en prendra 8. Ou 16, ou 32...

Par contre, avec Arduino (une version légère de C++), c'est possible. C'est à cause d'un dépassement que le robot de l'activité 1 retournait à une vitesse de 0.

La vitesse maximale 1111 1111 était encodée sur un octet (byte) et devenait 1 0000 0000 lorsqu'on tentait de l'incrémenter.

1111 1111
+ 1
-------------
= 1 0000 0000

3.4 Détection de dépassement sur l'addition d'entiers naturels

Voir

Puisque Python gère les débordements automatiquement, c'est qu'il y a un moyen de prévoir qu'il va y avoir dépassement.

Dépassement sur l'addition

L'un des moyens de détecter si la somme C = A + B de deux entiers A et B a provoqué un dépassement est d'utiliser ceci :

Avec des entiers naturels non nuls, le calcul de C = A + B n'a pas subi de dépassement si ces deux assertions sont vraies :

C > A
C > B

Si l'une des assertions ci-dessus est fausse, c'est que le résultat n'est pas bon !

Exemple

Sur deux octets, nous avions vu cet exemple :


     01000000 00000000  (A = 16384)
 +   11000000 00000010  (B = 49154)
 --------------------- 
 = 1 00000000 00000010  (C = A + B = 2 sur deux octets !)

Ici, nous aurions C = A + B évaluée à 2 en ne tenant compte que des deux octets de base.

Le dépassement est facilement détectable par un système informatique : 2 n'est pas supérieur ou égal à 16384. La première assertion est donc fausse.

3.5 Détection de dépassement sur la multiplication d'entiers naturels

Voir

Plus compliqué à détecter que l'addition

Sur un calcul sur deux octets, 400 * 500 donne 3392 plutôt que 200 000. C'est un dépassement, mais on ne peut pas le découvrir aussi simplement qu'avec une addition : la valeur obtenue 3392 est plus grande que 400 et 500...


      00000001 10010000  (A, 400)
 *    00000001 11110100  (B, 500)
 ----------------------
 = 11 00001101 01000000  (C, 3392 sur 2 octets !)

Avec 2 octets, on ne peut aller que jusqu'à 65535. On sait donc bien que 200 000 ne tiendrait pas. Mais pour savoir que c'est 200 000, il faut avoir fait le calcul... Alors comment faire ?

Dépassement sur la multiplication

La détection est assez simple mais il faut y penser : on prend le résultat fourni par le système informatique, on réalise une division dans l'autre sens et on vérifie qu'on retombe sur le résultat attendu.

Avec des entiers naturels non nuls, le calcul de C = A * B n'a pas subi de dépassement si cette assertion est vraie :

C // A == B, avec A non nul

Cela signifie que le calcul de C // A doit redonner B.

On remarquera qu'on aurait pu prendre plutôt C // B == A, avec B non nul.

Exemple

Exemple avec 400*500 qui donne 3392 sur deux octets.


      00000001 10010000  (A, 400)
 *    00000001 11110100  (B, 500)
 ----------------------
 = 11 00001101 01000000  (C, 3392 sur 2 octets !)

Assez facile à détecter.

C donne 3392.
A vaut 400, c'est bien différent de 0.
On évalue C // A = 3392 // 400, on obtient 8.
Puisque 8 ne vaut pas B (500), on peut en déduire que la multiplication n'a pas fonctionné et qu'il y a eu un problème de dépassement.

Nous aurions pu travailler plutôt avec B :

On évalue C // B = 3392 // 500, on obtient 6.
Puisque 6 ne vaut pas A (400), on peut en déduire qu'il y a eu dépassement.

18° Déterminer (sans faire le calcul direct bien entendu) si il y a ou non dépassement lors les calculs suivants, tous réalisés sur 16 bits :

On considère l'addition de A = 16000 par B = 2000. On obtient C = 18000.
On considère la multiplication de A = 16000 par B = 2000. On obtient C = 18432.
On considère la multiplication de A = 1600 par B = 2000. On obtient C = 54272.
On considère la multiplication de A = 160 par B = 2000. On obtient C = 57856.
On considère la multiplication de A = 16 par B = 2000. On obtient C = 32000.

Correction ?

...CORRECTION...

On considère l'addition de A = 16000 par B = 2000. On obtient C = 18000.

A et B sont non nuls.

Aucun dépassement puisque 18000 > 16000 et 18000 > 2000.

On considère la multiplication de A = 16000 par B = 2000. On obtient C = 18432.

On a A = 16000 qui est donc non nul.

Si on calcule C // A, on obtient 18432 // 16000, soit 1 puisque c'est une division euclidienne.

Nous avons donc eu un dépassement puisqu'on n'obtient pas la bonne valeur de B, 2000 en calculant C // A.

On considère la multiplication de A = 1600 par B = 2000. On obtient C = 54272.

On a A = 1600 qui est donc non nul.

Si on calcule C // A, on obtient 54272 // 1600, soit 33 puisque c'est une division euclidienne.

Nous avons donc eu un dépassement puisqu'on n'obtient pas la bonne valeur de B, 2000 en calculant C // A.

On considère la multiplication de A = 160 par B = 2000. On obtient C = 57856.

On a A = 160 qui est donc non nul.

Si on calcule C // A, on obtient 57856 // 160, soit 174 puisque c'est une division euclidienne.

Nous avons donc eu un dépassement puisqu'on n'obtient pas la bonne valeur de B, 2000 en calculant C // A.

On considère la multiplication de A = 16 par B = 2000. On obtient C = 32000.

On a A = 16 qui est donc non nul.

Si on calcule C // A, on obtient 32000 // 16, soit 2000 puisque c'est une division euclidienne.

Nous avons donc le bon résultat de B attendu, il n'y pas eu dépassement.

3.6 Simuler un calcul sur X bits avec Python

Voir

Principe sur 16 bits

Pour simuler un dépassement sur un calcul d'entiers 16 bits en Python, il suffit de faire ce calcul :


>>> (16000*2000) % 65536
18432

Pourquoi 65536 ? Tout simplement car il s'agit du nombre de cas possibles avec 2 octets (16 bits) : 2¹⁶ ou 256².


>>> (16000*2000) % 2**16
18432

Gestion d'une addition sur X bits

Nous allons pour cela utiliser le mot-clé assert qui permet de vérifier une assertion, une propriété normalement vraie.

Python vérifie l'assertion, continue son chemin si elle est vraie et provoque l'arrêt prématuré du programme sinon en déclenchant une erreur nommée AssertionError.

def addition(a, b, x):
	"""Simule une addition a+b sur x bits"""
	c = (a + b) % 2**x
	assert c > a  # Provoque l'arrêt si le test est faux
	assert c > b  # Provoque l'arrêt si le test est faux
	return c

Exemples d'utilisation


>>> addition(200, 40, 8)
240
 
>>> addition(200, 50, 8)
250
 
>>> addition(200, 60, 8)
AssertionError

Gestion d'une multiplication sur X bits

def multiplication(a, b, x):
	"""Simule une multiplication a*b NONS NULS sur x bits"""
	c = (a * b) % 2**x
	if a != 0:
		assert c // a == b # Provoque l'arrêt si le test est faux
	else:
		assert c == 0 # Provoque l'arrêt si le test est faux
	return c

Exemples d'utilisation


>>> multiplication(2, 100, 8)
200
 
>>> multiplication(0, 100, 8)
0
 
>>> multiplication(3, 100, 8)
AssertionError

19° On considère la multiplication de A = 22000 par B = 1250 sur 32 bits. On obtient C = 27500000.

Déterminer (sans faire le calcul direct bien entendu) si il y a ou non dépassement.
Simuler ensuite le résultat du calcul sur 16 bits (2 octets) comme ci-dessous. Le calcul est-il bon ?.

>>> (22000*1250) % (2**16)

Correction ?

...CORRECTION...

Déterminer (sans faire le calcul direct bien entendu) si il y a ou non dépassement.

On a A = 22000 qui est donc non nul.

Si on calcule C // A, on obtient 27500000 // 22000, soit 1250 puisque c'est une division euclidienne.

Nous avons donc le bon résultat de B attendu, il n'y pas eu dépassement.

Simuler ensuite le résultat du calcul sur 16 bits (2 octets) comme ci-dessous. Le calcul est-il bon ?.

>>> (22000*1250) % (2**16)
40416

On a A = 22000 qui est donc non nul.

Si on calcule C // A, on obtient 40416 // 22000, soit 1 puisque c'est une division euclidienne.

Nous avons dépassement, puisqu'on obtient pas le B attendu, 1250.

On a B = 2000 qui est donc bien différent de 0.

Si on calcule C // A, on obtient 32 000 000 // 16000, soit 2000 puisque c'est une division euclidienne.

Nous n'avons donc pas eu de dépassement et 32 000 000 est le bon résultat.

Avec 3 octets, on a 24 bits (3*8). La valeur maximale est donc 2²⁴-1, soit 16 777 215.

Nous aurions donc eu un mauvais résultat dû à un dépassement puisque le vrai résultat de 32 millions est supérieur à la capacité maximale de 16 777 215 avec 24 bits.

On aurait alors obtenu :


>>> (16000*2000) % (2**24)
15222784

20° Voici un exercice de synthèse final.

On veut multiplier les entiers A et B dont on vous donne l'encodage sur 4 octets.

Questions

A combien de bits correspondent 4 octets ?
Donner la valeur de A à l'aide de ses 4 octets : 200 50 0 250 .
Donner la valeur de B à l'aide de ses 4 octets : 5 10 20 150 .
Expliquer s'il y a eu dépassement lors du calcul par le programme sachant que A * B donne C = 556014204.
Donner le résultat C = A * B en le réalisant sur la console Python. Vérifier que Python réponde bien C = 283 968 746 947 877 500. Expliquer s'il y a eu dépassement lors de ce calcul.
Combien d'octets sont nécessaires à ce calcul ? 1, 2, 4, 8 ou 16 ?

Correction ?

...CORRECTION...

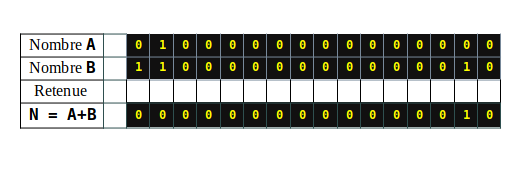
A combien de bits correspondent 4 octets ?

8 bits par octet. Il faut donc 4*8 = 32 bits.

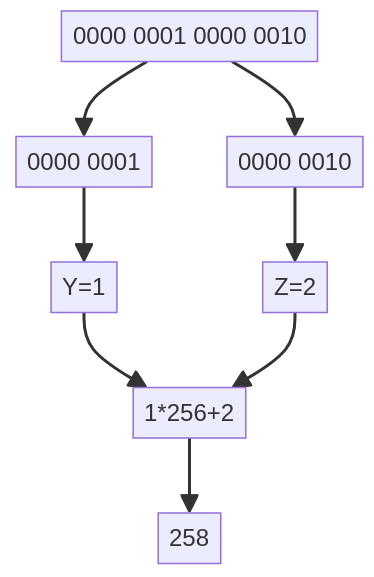
Donner la valeur de A à l'aide de ses 4 octets : 200 50 0 250 .

A = 200*256**3 + 50*256**2 + 0*256 + 250

A = 3 358 720 250

Plus de 3 milliards.

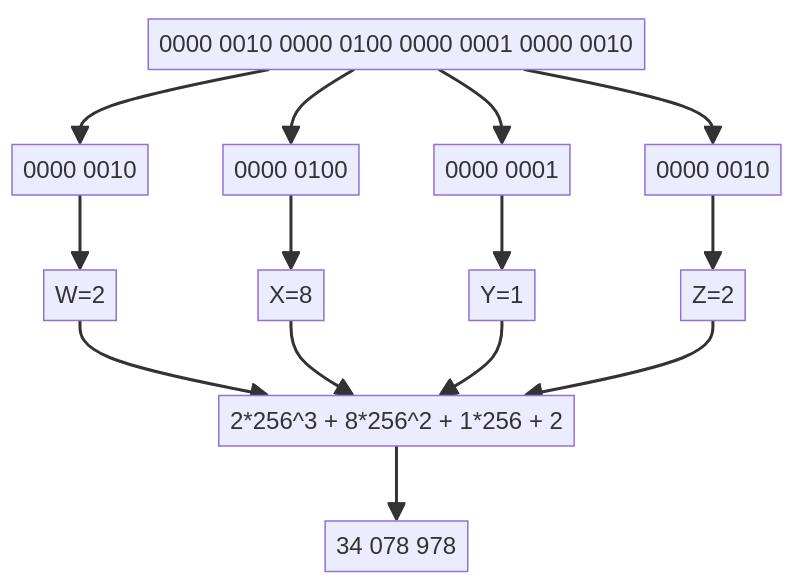
Donner la valeur de B à l'aide de ses 4 octets : 5 10 20 150 .

B = 5*256**3 + 10*256**2 + 20*256 + 150

B = 84 546 710

Plus de 84 millions.

Expliquer s'il y a eu dépassement lors du calcul par le programme sachant que A * B donne C = 556014204.

On peut effectuer la vérification puisque B n'est pas nul. On peut vérifier que C // B donne bien A (pour changer un peu).

C // B = 556014204 // 84546710 = 6

On n'obtient pas la valeur de A. Nous avons donc subi un dépassement.

Donner le résultat C = A * B en le réalisant sur la console Python. Vérifier que Python réponde C = 283 968 746 947 877 500. Expliquer s'il y a eu dépassement lors de ce calcul.


>>> C = 3358720250 * 84546710
>>> C
283968746947877500
 
>>> C // 84546710
3358720250

On peut effectuer la vérification puisque B n'est pas nul. On peut vérifier que C // B donne bien A (pour changer un peu).

C // B = 283 968 746 947 877 500 // 84546710 = 3 358 720 250

On obtient bien la valeur de A. Python a réalisé le calcul sans dépassement.

Combien d'octets sont nécessaires à ce calcul ? 1, 2, 4, 8 ou 16 ?

On doit obtenir 283 968 746 947 877 500, soit plus de 283 millions de milliards. C'est beaucoup...


>>> C = 3358720250 * 84546710
>>> C
283968746947877500
 
>>> C // 1E9
283968746.0
 
>>> C // 1E15
283.0

Avec un octet, on peut aller jusqu'à 2⁸-1, soit 255.

Pas suffisant.

Avec deux octets, on peut aller jusqu'à 2¹⁶-1, soit 65 535.

Pas suffisant.

Avec quatre octets, on peut aller jusqu'à 2³²-1, soit 4 294 967 295

Plus de 4 milliards.

Pas suffisant.

Avec huit octets, on peut aller jusqu'à 2⁶⁴-1, soit 18 446 744 073 709 551 615.

Plus de 18 milliards de milliards.

C'est suffisant.

4 - FAQ

⇩ ⇧ ⤊

J'ai vu qu'en C ou en Java, il y a plein de types d'intégers.

En fonction du nombre d'octets voulus pour le stockage, il existe souvent plusieurs types d'integers. Selon les langages de programmation, les noms et les tailles correspondantes sont variables.

Dans la plupart des langages, il existe des integers qu'on nomme :

byte : en Arduino, on stocke un entier sans signe (non signé) sur un seul octet. On peut donc encoder des nombres allant de 0 à 255. En Java, il se nomme unsigned byte.
unsigned short : 2 octets (16 bits) en Java, au moins 2 octets en C (valeur exacte fonction du processeur).
unsigned int : 4 octets (32 bits) en Java, au moins 2 octets en C (valeur exacte fonction du processeur).
unsigned long : 8 octets (64 bits) en Java, au moins 4 octets en C (valeur exacte fonction du processeur).
unsigned long long : au moins 8 octets en C (valeur exacte fonction du processeur).

En Python, c'est plus facile pour l'utilisateur : il n'y a que le type int. C'est l'interpréteur qui se charge de choisir le nombre d'octets nécessaires pour toutes nouvelles affectations.

En Javascript, c'est encore plus simple : il n'y a même pas de type int et float mais uniquement un type number !

J'ai entendu parler de big endian et little endian... C'est quoi ce truc ?

Imaginons qu'on veuille stocker N = 25800 en mémoire. Plus grand que 255 mais inférieur à 65535, on peut donc se contenter de deux octets.

N = 100*256 + 200 = 25800

On a donc les deux octets 100 200 .

100 en tant qu'octet de poids fort et 200 en tant qu'octet de poids faible.

Un problème technique arrive lorsqu'on veut stocker puis relire un contenu composé de plusieurs octets : il faut savoir dans quel ordre on les reçoit !

On nomme cela le boutisme.

En gros boutisme ou big endian, l'octet de poids fort est écrit et lu en premier.

L'octet de poids fort 100 apparaît en premier lors de la lecture des octets en mémoire :

-->-- -->-- -->-- -->-- -->-- -->--
xxx xxx 100 200 xxx xxx

On en déduit N = 100 200 .

En petit boutisme ou little endian, l'octet de poids faible est écrit et lu en premier.

L'octet de poids fort 100 apparaît en dernier lors de la lecture des octets en mémoire :

-->-- -->-- -->-- -->-- -->-- -->--
xxx xxx 200 100 xxx xxx

On doit donc inverser les octets lus et on en déduit N = 100 200 aussi. Ouf.

Il est donc nécessaire de savoir comment ont été stockés ces deux octets si on veut savoir ce qu'ils encodent vraiment.

Activité publiée le 22 09 2019
Dernière modification : 23 12 2023
Auteur : ows. h.

⏪

⏫

⏩