Quelques exercices sur les arbres avant d'aborder les algorithmes qui nous permettront de traiter les données contenues dans les noeuds, données identifiées par un élément qu'on nomme parfois
Documents de cours : open document ou pdf
Exercices supplémentaires 🏠 : Exercices
Un arbre enraciné est un noeud (racine) portant une étiquette et menant à 0, 1 ou plusieurs noeuds enfants.
Un arbre binaire est :
01° Donner la racine de l'arbre, la taille de l'arbre et la hauteur de l'arbre en considérant que la hauteur de la racine est de 1.
Terminer en donnant le nombre de feuilles.
...CORRECTION...
La racine est le noeud noté HTML.
Taille de 23 car 23 noeuds.
Si on prend une profondeur de 1 pour la racine, on obtient une hauteur d'Arbre de 5.
On compte 15 feuilles.
02° Pourquoi ne peut-on pas considérer qu'il s'agit d'un Arbre Binaire ? Comment nomme-t-on ce type d'arbre qui possède une hiérarchie ?
Quel critère est ici utilisé pour créer la hiérarchie ?
...CORRECTION...
Non : certains noeuds ont plus de 2 fils.
Il s'agit d'une arborescence.
Le critère de sélection est le fait que certaines balises sont contenues dans d'autres balises : la balise HTML contenant toutes les autres balises, elle est la racine.
03° Alice désire représenter ses ancêtres directs de cette façon.
Quelle est la taille de cet arbre ? Sa racine ? La hauteur de l'arbre ?
...CORRECTION...
La taille de l'arbre est 1+2+4 = 7.
La racine est le noeud Alice.
Sa hauteur est de 3 si on considère que la hauteur d'Alice est de 1.
04° En terme de nombre d'enfants par noeud, peut-on considérer qu'il s'agit d'un Arbre Binaire ? Est-ce suffisant ?
...CORRECTION...
Chaque noeud a bien deux enfants au maximum.
On peut ainsi dire que chaque arbre possède deux sous-arbres, au pire des arbres vides.
Mais pour dire qu'il s'agit d'un Arbre Binaire, il faut que la place d'un noeud à gauche ou à droite ai une signification.
05° Quelle est l'information encodée par la position gauche ou droite d'un enfant dans cet arbre ? Peut-on alors dire qu'il s'agit d'un arbre binaire ?
...CORRECTION...
Placer un noeud à gauche signifie qu'il s'agit d'un homme. Placer un noeud à droite signifie qu'il s'agit d'une femme.
Il s'agit donc bien d'un Arbre Binaire car on distingue le rôle d'un enfant-gauche et d'un enfant-droite.
06° Devinez quelle pourrait être l'information encodée par la position gauche ou droite d'un enfant dans cet autre Arbre Binaire...
Remarque : comme je signale qu'il s'agit d'un Arbre Binaire, gauche et droite ont nécessairement une signification.
...CORRECTION...
On place à droite un enfant dont le prénom-étiquette est du même sexe que le prénom-étiquette du noeud lui même.
Si le sexe est différent, il s'agit d'un fils gauche.
Le plus simple est d'apprendre par coeur ces trois formules, valables avec la convention profondeur 1 :
h = n (avec convention profondeur 1)
h = log2(n+1) (avec convention profondeur 1)
n = 2h - 1 (avec convention profondeur 1)
Les deux cas extrêmes sont :
A savoir : pour un arbre filiforme, l'ordre de grandeur de h est en n.
A savoir : pour un arbre parfait, l'ordre de grandeur de h est en lg(n).
Un arbre binaire quelconque est situé entre ces deux cas extrêmes. On peut encadrer la hauteur de l'arbre binaire quelconque à l'aide de l'une des formules suivantes.
Pour un arbre binaire quelconque :
⌈log2(n+1)⌉ ≤ h ≤ n (formule valable si profondeur 1 pour la racine)
Les signes ⌈ ⌉ indiquent un arrondi à l'entier supérieur (demi-crochets vers le haut).
>>> import math
>>> math.log2(15+1)
4.0
# n = 15 donc h=4 au minimum
>>> math.log2(16+1)
4.087462841250339
# Pour n = 16, on arrondi à 5 : h=5 au minimum
On voit alors qu'un arbre de 15 noeuds a une hauteur comprise dans [4; 15].
Par contre, avec 16 noeuds, on obtient une hauteur comprise dans [5;16].
C'est normal : avec 15 noeuds, l'arbre peut être parfait. Si on en rajoute un, il faut nécessairement rajouter un étage...
Pour un arbre binaire quelconque :
⌈log2(n+1)⌉ - 1 ≤ h ≤ n - 1 (formule valable si profondeur 0 pour la racine)
>>> import math
>>> math.log2(15+1)
4.0
# Pour n = 15, on calcule donc h=(4-1)=3 au minimum
>>> math.log2(16+1)
4.087462841250339
# Pour n = 16, on arrondit à 5 et on calcule h=(5-1)=4 au minimum
Ou encore cette autre formule :
⌊log2(n)⌋ ≤ h ≤ n - 1 (formule valable si profondeur 0 pour la racine)
Les signes ⌊ ⌋ indiquent un arrondi à l'entier inférieur (demi-crochets vers le bas).
>>> import math
>>> math.log2(15)
3.9068905956085187
Pour n=15, on arrondit donc à 3 et on a h=3 au minimum
>>> math.log2(16)
4.0
Pour n=16, on arrondit donc à 4 et on a h=4 au minimum
L'ordre de grandeur de la hauteur d'un Arbre Binaire est compris entre log2(n) et n.
07° Encadrer (sans calculatrice) la hauteur d'un Arbre Binaire quelconque possédant 120 noeuds. On prendra une profondeur de 0 pour la racine. Est-ce qu'il peut s'agir d'un Arbre Binaire parfait ?
⌈log2(n+1)⌉ - 1 ≤ h ≤ n - 1 (formule valable si profondeur 0 pour la racine)
...CORRECTION...
Profondeur 0 pour la racine : ⌈log2(n+1)⌉ - 1 ≤ h ≤ n - 1
La borne maximale est 119, facile (120-1).
Pour la borne minimale, il faut calculer log2(120+1). De tête !
Enfin, pas vraiment : il faut trouver l'arrondi au supérieur de log2(120+1) et retrancher un.
Or, on sait que :
Puisque la fonction logarithme est croissante, on peut donc en déduire que log2(121) est entre 6 et 7.
Si on arrondit au supérieur, on aura 7 et finalement 6 en retranchant 1.
On peut donc écrire ceci pour un Arbre Binaire quelconque de 120 noeuds
6 ≤ h ≤ 119
Il ne peut pas s'agit d'un Arbre Binaire parfait : il aura fallu 63 ou 127 noeuds.
08° Encadrer (sans calculatrice) la hauteur d'un Arbre Binaire quelconque possédant 50 noeuds. On prendra une profondeur de 1 pour la racine.
⌈log2(n+1)⌉ ≤ h ≤ n (formule valable si profondeur 1 pour la racine)
...CORRECTION...
Profondeur 1 pour la racine : ⌈log2(n+1)⌉ ≤ h ≤ n
La borne maximale est 50, facile.
Pour la borne minimale, il faut trouver log2(51)
On peut donc en déduire que log2(51) vaut 5 virgule quelque chose.
Si on arrondit au supérieur, on aura 6.
On peut donc écrire ceci pour un Arbre Binaire quelconque de 50 noeuds
6 ≤ h ≤ 50
09° Encadrer (sans calculatrice) la hauteur d'un Arbre Binaire quelconque possédant 34 noeuds. Attention, on prendra cette fois la formule pour une profondeur de 0 pour la racine.
⌊log2(n)⌋ ≤ h ≤ n - 1 (formule valable si profondeur 0 pour la racine)
...CORRECTION...
Profondeur 0 pour la racine :⌊log2(n)⌋ ≤ h ≤ n - 1
La borne maximale est 33 (n-1), facile.
Pour la borne minimale, il faut trouver l'arrondi inférieur de log2(34)
On peut donc en déduire que log2(34) vaut 5 virgule quelque chose.
Si on arrondit à l'inférieur, on aura 5.
On peut donc écrire ceci pour un Arbre Binaire quelconque de 34 noeuds
5 ≤ h ≤ 33
10° Quelle est la taille d'un Arbre Binaire Parfait de hauteur 0, 1, 2 jusqu'à 5 si on considère que la profondeur de la racine est de 0 ?
Trouver (sans la démontrer) la formule permettant de calculer directement cette taille n connaissant h.
...CORRECTION...
Pour une profondeur de racine de 0 :
Hauteur h = 0 : Taille n = 1, facile.
Hauteur h = 1 : Taille n = 1 + 2 = 3
Hauteur h = 2 : Taille n = 1 + 2 + 4 = 7
Hauteur h = 3 : Taille n = 1 + 2 + 4 + 8 = 15
Hauteur h = 4 : Taille n = 1 + 2 + 4 + 8 + 16 = 31
Hauteur h = 5 : Taille n = 1 + 2 + 4 + 8 + 16 + 32 = 63
On voit qu'il suffit de faire ceci :
n = 2h+1 - 1
11° Quelle est la taille d'un Arbre Binaire Parfait de hauteur 0, 1, 2 jusqu'à 5 si on considère que la profondeur de la racine est de 1 ?
Trouver (sans la démontrer) la formule permettant de calculer directement cette taille n connaissant h.
...CORRECTION...
Dans le cas d'une profondeur 1 pour la racine, on a
Hauteur h = 1 : Taille n = 1, facile.
Hauteur h = 2 : Taille n = 1 + 2 = 3
Hauteur h = 3 : Taille n = 1 + 2 + 4 = 7
Hauteur h = 4 : Taille n = 1 + 2 + 4 + 8 = 15
Hauteur h = 5 : Taille n = 1 + 2 + 4 + 8 + 16 = 31
Hauteur h = 6 : Taille n = 1 + 2 + 4 + 8 + 16 + 32 = 63
n = 2h - 1
12° Doit-on considérer cet Arbre comme un Arbre Binaire ou pas ? Que porte l'étiquette des noeuds-parents comme information ?
...CORRECTION...
A priori ici gauche et droite n'ont pas de signification réelle : les deux fils sont simplement les deux équipes qui se rencontrent et le père porte comme clé le nom de l'équipe qui a gagné.
Il s'agit donc d'un Arbre où chaque noeud-parent a au plus deux enfants mais il ne s'agit pas d'un Arbre Binaire a proprement parlé car on peut inverser la position gauche-droite d'un fils sans que cela n'ai de conséquence sur l'information stockée.
13° Dans un Arbre, des noeuds différents peuvent-ils porter des étiquettes identiques ?
...CORRECTION...
Oui, aucun problème.
On voit bien que l'étiquette France est attaché à trois noeuds différents.
14° Même si ce problème n'est pas exactement représentable comme un Arbre Binaire (si on ne donne pas de sens particulier à l'enfant gauche par rapport à l'enfant droite), peut-on utiliser les formules permettant de trouver n=f(h) ou h=f(n) pour un Arbre Binaire Parfait ?
...CORRECTION...
Oui : dans le cas des matchs, chaque noeud aura bien 2 enfants ou sera une feuille.
On peut donc utiliser les formules vues sur l'Arbre Binaire PArfait puisque la propriété de distinction n'a aucun rapport à la démonstration de la formule qui n'utilise que la notion de série géométrique.
15° Quelle est la hauteur de l'arbre qui représenterait une compétition du type précédent où il y aurait 64 équipes au départ (et donc 64 feuilles) ? On prendra une profondeur de 1 pour la racine.
...CORRECTION...
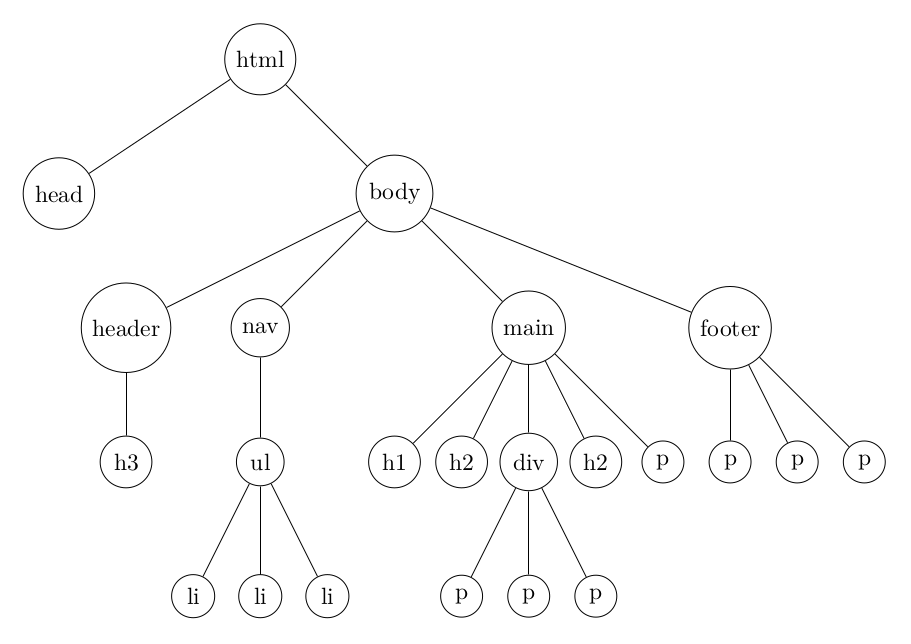
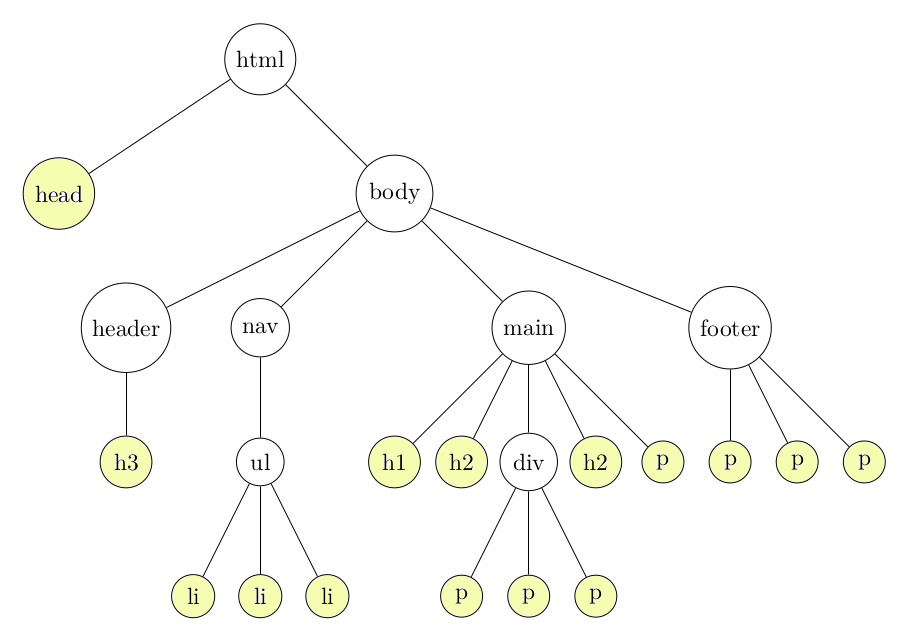
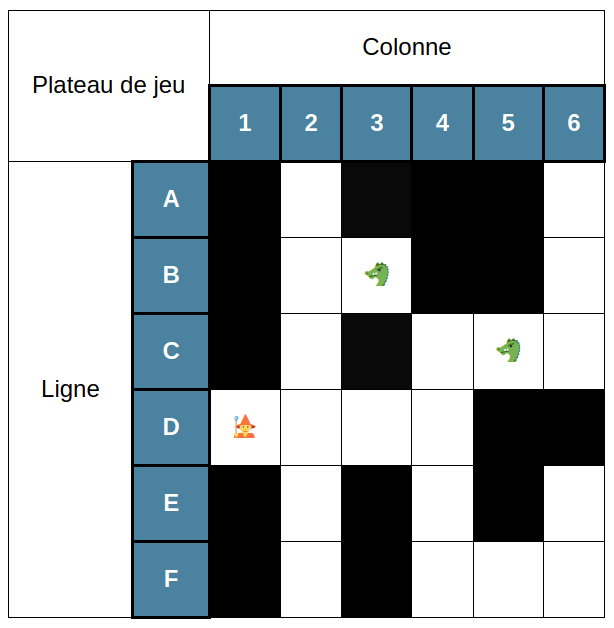
Il suffit de compter les étages pour obtenir la hauteur puisqu'il s'agit de l'équivalent d'un Arbre Binaire Parfait.
Les feuilles sont 64 (profondeur +1)
Au dessus, on trouve 32 noeuds (profondeur +2)
Puis encore 16 noeuds (profondeur +3)
Puis encore 8 noeuds (profondeur +4)
Puis encore 4 noeuds (profondeur +5)
Puis encore 2 noeuds (profondeur +6)
Puis la racine : si on lui donne une profondeur de 1, on obtient donc une hauteur de 7.
Nous aurions pu retrouver ce résultat en utilisant simplement la formule valable pour un arbre parfait (avec la convention profondeur 1):
h =
⌊ log2(n + 1) ⌋ =
⌊ log2(64+32+16+8+4+2+1 +1) ⌋ =
⌊ log2(128) ⌋ =
⌊ log2(27) ⌋ =
⌊ 7 ⌋ =
6
Si on considère que la profondeur de la racine est 0, on obtient 6. Si la profondeur est 1, on prendra 7.
Voici un mini-labyrinthe que nous avions utilisé pendant l'activité sur les matrices :
16° Dessiner l'arbre obtenu en prenant comme point de départ le magicien (c'est la racine). Déterminer la hauteur du labyrinthe. Déterminer alors les cases du plateau les plus éloignées où vous pourriez mettre la sortie.
17° Montrer, à partir de l'arbre, qu'on n'offre que 3 vrais choix au joueur et qu'il faut 8 mouvements au maximum pour sortir du labyrinthe.
Ce type de problèmes avec prise de décisions multiples est assez courant. Et à chaque fois, on en revient à une réprésentation sous forme d'arbres. Du coup, quelque soit le problème réel (un labyrinthe, un livre dont vous êtes le héros, une chaîne de production de voitures, un choix de position des thèmes dans un célèbre magasin d'ammeublements), on en revient à un simple arbre. Le tout, c'est qu'il n'y ai pas de boucles (sinon, c'est un problème de graphes).
Il est donc temps de voir comment parcourir ces arbres à l'aide de méthodes algorithmiques. La suite est donc dans la partie ALGO.
Activité publiée le 29 11 2020
Dernière modification : 29 11 2020
Auteur : ows. h.