11 - type abstrait de données Liste

⏪

⏬

⏩

1 - 1 Liste

2 - 2 Listes !

3 - Liste (Tête, Queue)

4 - Implémentation

5 - FAQ

L'an dernier, vous avez vu la différence entre un algorithme et son implémentation concrète en programme : un même algorithme peut être implémenté par un programme dans différents langages ou même en différentes versions de programmes pour un même langage. Tant que les programmes vont la même chose, l'utilisateur ne verra pas la différence.

ALGORITHME ⇒ Implémentation ⇒ PROGRAMME

Nous allons cette année faire la même chose pour les données : on fait travailler les algorithmes sur des types abstraits de données. On va ensuite les implémenter en machine sous différents types (implémentés).

ALGORITHME ⇒ Implémentation ⇒ PROGRAMME

TYPE ABSTRAIT ⇒ Implémentation ⇒ TYPE (implémenté)

Le mot structure de données fait lui référence à n'importe quel type de données ayant un rôle de conteneur et sur lequel on peut agir en utilisant des fonctions bien précises.

Conclusion de cette présentation

Les Types Abstraits vont nous permettre de résoudre les problèmes sans avoir à savoir comment les données sont réellement stockées et implémentées en machine.

Nous allons simplement nous concentrer sur les deux points fondamentaux suivants :

Comment classifier les données de notre problème ?
Comment utiliser ces données ?

Documents de cours : open document ou pdf

Exercices supplémentaires 🏠 : Exercices

MODE COURS (cacher les questions)

1 - La Liste en tant que type abstrait de données

⇩ ⇧ ⤊

1.1 1er partie de la définition de Liste : l'idée générale

Voir

A - Propriétés générales d'organisation

Le type abstrait Liste a les propriétés suivantes :

Une Liste est une structure LINÉAIRE composée d'une séquence finie et ordonnée de Places contenant chacune un Élement . Si on réalise une analogie avec une armoire à casiers ou dossiers suspendus :

L'armoire est la Liste
Chaque casier ou dossier suspendu est une Place
Chaque objet placé dans un casier ou un dossier suspendu est un Élément

On doit pouvoir insérer et supprimer au moins une Place (au choix du concepteur : au début, ou à la fin, ou partout...)
On doit pouvoir accéder à toutes les Places.
On doit pouvoir lire un Elément en connaissant la Place qu'il occupe
On doit pouvoir trouver le successeur unique de chaque Place : en partant d'un casier on doit pouvoir trouver le casier suivant.

On peut donc accéder librement à n'importe quelle donnée de la Liste.

Remarque

Ici, les propriétés ont été données sous forme de simples phrases mais vous verrez dans le supérieur qu'il est possible de les décrire sous forme de propriétés mathématiques.

B - Vocabulaire

La première Place de la Liste est nommée tête (head en anglais).
L'ensemble des autres Places de la Liste forme la queue (tail en anglais).
La dernière Place de la Liste est nommée fin. Attention, on trouve parfois également le mot queue pour désigner la fin. Ici, nous utiliserons bien uniquement fin.
L'indice d'une Place correspond au nombre de sauts nécessaires pour l'atteindre à partir de la tête : la tête est à l'indice 0, la suivante 1...
La Liste est homogène si tous les éléments stockés sont de même type. Sinon elle est inhomogène.

C - Exemple

On considère une Liste dont

La Tête est 5
La Queue est 8 → 2 → 3

Deux façons de la représenter :

5 → 8 → 2 → 3
3 ← 2 ← 8 ← 5

Vous répondrez aux questions 01 à 05 sous la forme de d'un tableau à quatre colonnes :

Question	Tête	Queue	Fin
01
...
05

01° Sur la Liste, ci-dessous :

Quel est l'élément contenu dans la tête ?
Quelle est la séquence d'éléments qui forme la queue ?
Quel est l'élément contenu dans la fin ?

12 → 4 → 5 → -15

Correction ?

...CORRECTION...

La tête est ici identifiée par la couleur ET le sens des flèches.

La tête contient donc l'élément 12.

La queue est donc composée de la séquence (4, 5, -15).

La fin référence -15.

02° Sur la Liste, ci-dessous :

Quel est l'élément contenu dans la tête ?
Quelle est la séquence d'éléments qui forme la queue ?
Quel est l'élément contenu dans la fin ?

23 ← 12 ← 460 ← 1

Correction ?

...CORRECTION...

La tête est ici identifiée par la couleur ET le sens des flèches.

La tête contient donc 1.

La queue est donc composée de (460, 12, 23).

La fin référence 23.

03° Idem mais sans couleur :

Quel est l'élément contenu dans la tête ?
Quelle est la séquence d'éléments qui forme la queue ?
Quel est l'élément contenu dans la fin ?

21 → 12 → 13 → 0

Correction ?

...CORRECTION...

La tête est ici identifiée par le sens des flèches : c'est le premier élément.

La tête contient donc 21.

La queue est donc composée de (12, 13, 0).

La fin référence 0.

04° Idem mais sans couleur :

Quel est l'élément contenu dans la tête ?
Quelle est la séquence d'éléments qui forme la queue ?
Quel est l'élément contenu dans la fin ?

20 ← 45 ← 10 ← 18

Correction ?

...CORRECTION...

La tête est ici identifiée par le sens des flèches : c'est le premier élément.

La tête contient donc 18.

La queue est donc composée de (10, 45, 20).

La fin référence donc 20.

05° Seule la tête est indiquée. Mêmes questions :

Quel est l'élément contenu dans la tête ?
Quelle est la séquence d'éléments qui forme la queue ?
Quel est l'élément contenu dans la fin ?

23 - 12 - 460 - 1

Correction ?

...CORRECTION...

La tête est ici identifiée par la couleur.

La tête contient donc 1.

La queue est donc composée des éléments situés linéairement derrière cette tête : (460, 12, 23).

La fin référence donc 23.

1.2 Représentations d'une Liste

Voir

A - Représentation graphique Tête → Queue

Une Liste NON VIDE est fondamentalement une tête menant à une queue.

5 → 8 → 2 → 3

Si le 5 est la tête d'une Liste nommée lst1, on peut noter sa queue lst2.

5 → lst2

On pourrait alors noter ceci : lst1 = (5, lst2).

D'ailleurs, lst2 est également une Liste : sa tête contient 8 et mène à une queue lst3...

8 → lst3

lst2 = (8, lst3)

On obtient alors l'enchaînement suivant, qui est assez proche des appels de fonctions récursives :

lst1 = (5, lst2)
lst2 = (8, lst3)
lst3 = (2, lst4)
lst4 = (3, lst5)
lst5 = ()

B - Définition (en français)

Une Liste peut être :

soit une liste vide (c'est le cas de base)
soit un couple (tête, queue), la queue étant elle-même une liste (c'est le cas récursif)

On pourrait remonter dans l'autre sens dans nos déclarations et obtenir ceci :

lst4 = (3, ())
lst3 = (2, (3, ()))
lst2 = (8, (2, (3, ())))
lst1 = (5, (8, (2, (3, ()))))

Remarquez bien que la queue de lst4 est vide. C'est possible puisque qu'une queue est une liste et qu'une liste peut être vide.

C - Définition formelle (en mathématique)

Liste = ListeVIDE | (Element, Liste)

On remarque immédiatement la nature récursive d'une Liste puisque pour définir le mot Liste, on utilise le mot Liste.

D - Représentations : imbrication ou séquence ordonnée

On peut représenter de façon abstraite les listes soit comme des imbrications, soit comme des séquences ordonnées. Reste le choix du symbole pour définir le début et la fin d'une déclaration :

Avec des parenthèses : (5, (8, (2, (3)))) ou plus facilement par (5, 8, 2, 3)

Avec des crochets : [5, [8, [2, [3]]]] ou plus facilement par [5, 8, 2, 3]

Avec chevrons : <5, <8, <2, <3>>>> ou plus facilement par <5, 8, 2, 3>

Avec des accolades : {5, {8, {2, {3}}}} ou plus facilement par {5, 8, 2, 3}

On évitera cette notation "accolades" car on pourrait confondre avec les ensembles mathématiques, où un élément ne peut être présent qu'une fois. Or, dans une liste, une même valeur peut être présente plusieurs fois.

Il faut juste choisir, le noter clairement.

Dans le cadre de ce cours, nous utiliserons les parenthèses et placerons la tête à gauche systématiquement.

(5, 8, 2, 3)

E - Représentation de la liste VIDE

De la même façon, on peut choisir de représenter, ou pas, la Liste VIDE.

Les deux représentations ci-dessous représentent donc strictement la même Liste :

(5, 8, 2, 3)

(5, 8, 2, 3, VIDE)

06° Donner deux représentations de la liste suivante :

comme une imbrication (tête, queue)
comme une simple séquence linéaire d'éléments :

12 → 4

Correction ?

...CORRECTION...

En représentation (tête, queue)

(12, (4, ()))

En séquence linéaire : (12, 4, vide)

07° Donner deux représentations de la liste suivante :

comme une imbrication (tête, queue)
comme une simple séquence linéaire d'éléments :

5 → 2 → 10

Correction ?

...CORRECTION...

Première représentation

(5, (2, (10, ())))

La deuxième représentation est donc (5, 2, 10, vide).

1.3 Signatures et erreur de Type

Voir

A - Signature : définition

Une signature est une formulation précise de la syntaxe et des types pour utiliser correctement un opérateur ou une fonction. Elle signale :

le symbole de l'opérateur ou le nom de la fonction
les types des entrées
où placer les entrées par rapport à l'opérateur ou lors de l'appel d'une fonction
le type de la réponse

Exemple 1 : signature de la fonction native len() :

len(str) → int
len(list) → int
len(tuple) → int
len(dict) → int
len(str|list|tuple|dict) → int

Le signe | (touche ALT-GR 6) symbolise le OU.

Exemple 2 : quelques signatures disponibles sur les strings en Python :

str + str → str
str * int → str
int * str → str
str in str → bool
str in list → bool
str < str → bool
str.lower() → str

Intérêt :

Lorsqu'on respecte une signature, il n'y aura pas d'erreur de SYNTAXE. La demande est correctement formulée.
C'est comme cela que Python sait si une expression que vous transmettez est "valide" ou non. L'interpréteur cherche à trouver un motif correspondant à une signature connue.
Il s'agit de contraintes liées uniquement au type, pas au contenu réel envoyé : même si le contenu est du bon type, il peut y avoir une erreur d'EXÉCUTION.

B - Signature non valide : erreur de Type


>>> "Pom !" * 4
'Pom ! Pom ! Pom ! Pom !'
 
>>> "Pom !" * 4.0
TypeError: can't multiply sequence by non-int of type 'float'

Selon les langages, l'erreur de type sera détectée avant l'exécution ou pendant l'exécution.

Python les détecte pendant l'exécution de l'expression problématique. Il est donc possible que le problème n'apparaisse pas pendant les tests mais apparaisse en production...
Ocaml les détecte avant exécution. Le problème sera donc mis en évidence dès la conception du programme.

C - Signature valide

Respecter une signature implique qu'il n'y aura pas d'erreur de SYNTAXE.

Par contre, il peut encore y avoir une erreur d'EXÉCUTION ou une erreur SÉMANTIQUE.

Exemple d'erreur d'EXÉCUTION : la signature int // int → int existe mais :


>>> 6 // (5 - 5)
ZeroDivisionError: division by zero

Ici, nous avons bien une erreur d'exécution : la signature est bonne mais pas l'exécution de la demande.

Exemple d'erreur SÉMANTIQUE : la signature float + float → float existe mais également la signature tuple + tuple → tuple !


>>> 6,2 + 1,3
(6, 3, 3)

Ici, nous avons bien une erreur sémantique si vous avez voulu additionner deux flottants : vous avez oublié que c'est le point qui fait office de virgule et Python a lui traité la demande comme ce qu'elle veut dire : elle a utilisé la deuxième signature puisque pour lui 6,2 est le tuple (6, 2).


>>> 6,2
(6, 2)

08° Taper ceci dans la console Python et, pour chaque opération :

Dire si l'opération est acceptée ou pas (exemple int + str : Non acceptée).
Si elle existe, donner la signature fournie par cette syntaxe (exemple int + int -> int )
Si elle existe, donner la sémantique de cette signature (exemple : ADDITION : int + int -> int ).

>>> 46 // 10
 
>>> 46 % 10
 
>>> [46] + [10]
 
>>> [46] * [10]
 
>>> [46] * 10

Correction ?

...CORRECTION...

>>> 46 // 10
4

Quotient d'une division euclidienne : int // int -> int

>>> 46 % 10
6

Reste d'une division euclidienne : int % int -> int

>>> [46] + [10]
[46, 10]

Concaténation : list + list -> list

>>> [46] * [10]
TypeError: can't multiply sequence by non-int of type 'list'

Signature non acceptée : list * list

>>> [46] * 10
[46, 46, 46, 46, 46, 46, 46, 46, 46, 46]

Répétition : list * int -> list

1.4 Spécification d'une fonction

Voir

Le respect de la signature permet d'éviter les erreurs de syntaxe et de type, mais pas certaines erreurs d'exécution.

Pour éviter les erreurs d'exécution, il faut fournir une spécification : une description encore plus précise de la fonction.

La SPECIFICATION d'une fonction contient :

son NOM,
sa SIGNATURE,
une DESCRIPTION textuelle de ce que fait cette fonction.
les éventuelles PRECONDITIONS : quelles sont les conditions supplémentaires en plus du simple type (entier NON NUL, texte SANS ESPACE...) que le concepteur demande sur les entrées.
les éventuelles POSTCONDITIONS : quelles sont les propriétés supplémentaires que le concepteur garantit sur la sortie.

1.5 Opérations primitives

Voir

Deux idées caractérisent ces fonctions particulières :

Les opérations primitives sont les actions fondamentales permettant d'agir sur ce type de données.

En combinant les primitives, on doit pouvoir créer toutes les autres opérations permettant d'agir sur ce type.

Même si la notion de coût n'existe pas réellement pour une idée abstraite, les futures implémentations des primitives devront avoir le coût le plus faible possible (un coût constant si possible).

1.6 2nd partie de la définition de Liste : spécifications des primitives

Voir

A - Dépendances du type abstrait Liste

Pour définir notre Liste, nous allons avoir besoin des autres types suivants (ce sont les dépendances) :

Vide pour référencer l'absence d'information,
Booléen,
Entier Naturel,
Elément (le type des données que nous allons pouvoir ranger dans la Liste),
Place (le conteneur permettant de stocker un Elément). On décide du fait qu'une Place ne peut pas être vide : si elle existe, c'est qu'elle contient un Element.

B - Spécifications : définition

Voici les primitives d'une Liste immuable.

Fondamentales

nLV() ou nouvelleListeVide() → Liste VIDE

Renvoie une nouvelle Liste VIDE initialement.

estLV() ou estListeVide(lst:Liste) → Booléen

Prédicat qui renvoie VRAI si la liste lst fournie est vide, FAUX sinon.

ins() ou inserer(lst:Liste, elt:Elément, ...) → Liste NON VIDE

Renvoie une nouvelle Liste comportant le nouvel élément à une position choisie. Certaines valeurs seront donc décalées par rapport à la Liste initiale.

POSTCONDITIONS : la Liste renvoyée est NON VIDE et possède un emplacement en plus mais lst est inchangée.

Voici plusieurs versions qui pourraient convenir, la première étant la plus générique :

ins() ou inserer(lst:Liste, elt:Elément, i:Entier Naturel VALIDE) → Liste NON VIDE

Renvoie une nouvelle Liste comportant le nouvel élément à la position indiquée par l'indice fourni.

insT() ou insererTete(lst:Liste, elt:Elément) → Liste NON VIDE

Renvoie une nouvelle Liste où l'élément est placé en tête de liste, provoquant le décalage de tous les autres élements.

Equivalent à un appel à ins() en lui envoyant i=0.

insF() ou insererFin(lst:Liste, elt:Elément) → Liste NON VIDE

Renvoie une nouvelle Liste où l'élément est placé en fin de liste.

Equivalent à un appel à ins() en lui envoyant i=longueur puisque les indices possibles de la liste vont de 0 à longueur-1 avant insertion.

Un appel à ins() en lui envoyant i=longueur-1 veut dire qu'on veut placer l'élément en avant dernière position, l'ancienne fin est toujours la même.

Exemples d'utilisation

lstA = nouvelleListeVide()
lstB = inserer(lstA, 5, 0)
lstB contient alors (5, () ) qu'on pourrait noter (5, VIDE).

lstC = inserer(lstB, 15, 0)
lstC contient alors (15, (5, () )) qu'on pourrait noter (15, 5, VIDE).

lstD = inserer(lstC, 25, 1)
lstD contient alors (15, (25, (5, () ))) qu'on pourrait noter (15, 25, 5, VIDE).

lstE = inserer(lstD, 50, 3)
lstE contient alors (15, (25, (5, (50, () )))) qu'on pourrait noter (15, 25, 5, 50, VIDE).

sup() ou supprimer(lst:Liste NON VIDE, ...) → Liste

Renvoie une nouvelle Liste dans laquelle on a supprimé un emplacement prédéfini dans la Liste NON VIDE reçue. Certains emplacements sont donc décalés d'une position par rapport à la Liste initiale.

PRECONDITION : la Liste reçue est NON VIDE.

POSTCONDITION : la Liste renvoyée possède un emplacement en moins mais lst est inchangée.

Voici plusieurs versions qui pourraient convenir, la première étant la plus générique :

supprimer(lst:Liste NON VIDE, i:Entier Naturel vALIDE) → Liste

Renvoie une nouvelle Liste dans laquelle on a supprimé l'ancien emplacement ayant cet indice.

supT() ou supprimerTete(lst:Liste NON VIDE) → Liste

Renvoie une nouvelle Liste dans laquelle on a supprimé l'ancien emplacement en tête de liste.

Equivalent à un appel à sup() en lui envoyant i=0.

supF() ou supprimerFin(lst:Liste NON VIDE) → Liste

Renvoie une nouvelle Liste dans laquelle on a supprimé l'ancien emplacement en fin de liste.

Equivalent à un appel à sup() en lui envoyant i=longueur-1.

Exemple d'utilisation

Partons de lstE contenant (15, (25, (5, (50, () )))) ou (15, 25, 5, 50, VIDE).
lstF = sup(lstE, 1)
lstF contient alors (15, (5, (50, () ))) ou (15, 5, 50, VIDE).

lstG = sup(lstF, 2)
lstG contient alors (15, (5, () )) ou (15, 5, VIDE).

Importante si on utilise les indices

longueur(lst:Liste) → Entier Naturel

Renvoie le nombre d'éléments stockés dans la liste.

Interactions avec les Places

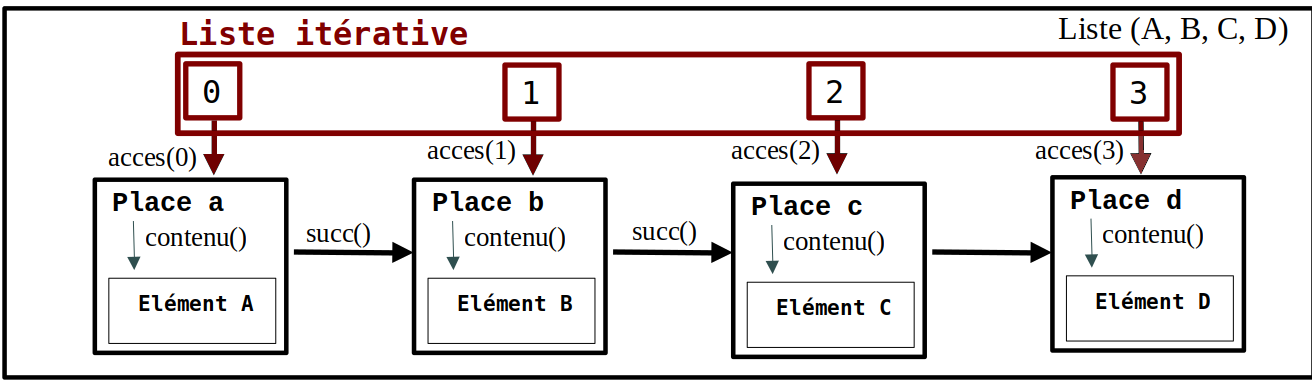
acc() ou acces(lst:Liste NON VIDE, ...) → Place

Renvoie la Place correspondant à une position définie.

POSTCONDITION : la Liste est inchangée.

Voici plusieurs versions qui pourraient convenir, la première étant la plus générique :

acc() ou acces(lst:Liste NON VIDE, i:Entier Naturel) → Place

Renvoie la Place correspondant à l'indice i fourni.

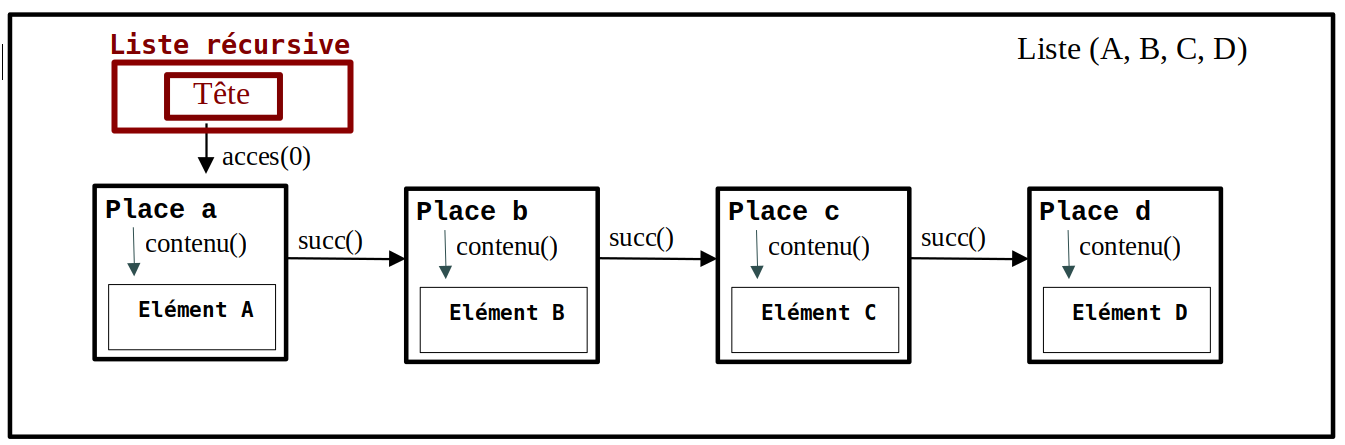
accT() ou accesTete(lst:Liste NON VIDE) → Place

Renvoie la Place correspondant à la tête.

Equivalent à un appel à acc() en lui envoyant i=0.

accF() ou accesFin(lst:Liste NON VIDE) → Place

Renvoie la Place correspondant à la fin.

Equivalent à un appel à acc() en lui envoyant i=longueur-1.

Les deux dernières primitives (numérotées 7 et 8 ici) interagissent directement avec une Place : la connaissance d'une Place doit venir de l'utilisation de acces().

contenu(plc:Place) → Elément

Renvoie l'Elément référencé par plc.

POSTCONDITION : si la Liste est homogène le type de l'Elément est compatible avec ceux de la Liste.

succ() ou successeur(plc:Place) → Place|Vide

Renvoie la Place qui succède à plc, ou l'information Vide si elle est la dernière.

Le type abstrait Liste possède donc une définition est plutôt large car

on n'explique pas vraiment ce qu'est une Place.
on n'impose pas spécifiquement d'endroit où agir. Il faut juste pouvoir agir à un endroit.

Toutes les structures de données qui collent à la définition et qui possèdent ces primitives sont donc des Listes.

Résumé : les 8 types de primitives qu'il faudra avoir ou reconstruire à partir des autres :

Fondamentales

nLV() ou nouvelleListeVide() → Liste VIDE
estLV() ou estListeVide(lst:Liste) → Booléen
ins() ou inserer(lst:Liste, elt:Elément, i:Entier Naturel VALIDE) → Liste NON VIDE
sup() ou supprimer(lst:Liste NON VIDE, i:Entier Naturel VALIDE) → Liste

Importante si on utilise les indices

longueur(lst:Liste) → Entier Naturel

Interactions avec les Places

acc() ou acces(lst:Liste NON VIDE, i:Entier Naturel VALIDE) → Place
contenu(plc:Place) → Elément
succ() ou successeur(plc:Place) → Place|Vide

09° Donner le contenu des variables au fur et à mesure de l'exécution de cette suite d'actions. Notez que j'utilise une syntaxe Python en tant que pseudo-langage algorithmique.

lstA = inserer(nouvelleListeVide(), 4, 0)
lstB = inserer(lstA, 6, 1)
lstB = inserer(lstB, 10, 0)
x = contenu(acces(lstB, 2))
lstC = supprimer(lstB, 2)
lstC = inserer(lstC, 100, 1)
a = contenu(successeur(acces(lstC, 0)))

Attention, ce n'est pas un algorithme : un algorithme doit résoudre un problème ou répondre à une question. Ici, il ne s'agit que d'une suite d'actions.

Correction ?

...CORRECTION...

lstA = inserer(nouvelleListeVide(), 4, 0)
lstB = inserer(lstA, 6, 1)
lstB = inserer(lstB, 10, 0)
x = contenu(acces(lstB, 2))

Ligne 1 : lstA contient (4, () ) ou (4, VIDE)

Ligne 2 : lstB contient (4, (6, () )) ou (4, 6, VIDE)

Ligne 3 : on modifie lstB en lui affectant la réponse de la fonction, qui contient (10, (4, (6, () ))) ou (10, 4, 6, VIDE)

Ligne 4 : x contient 6

5
6
7

lstC = supprimer(lstB, 2)
lstC = inserer(lstC, 100, 1)
a = contenu(successeur(acces(lstC, 0)))

Ligne 5 : lstC contient (10, (4, () )) ou (10, 4, VIDE)

Ligne 6 : lstC contient (10, (100, (4, () ))) ou (10, 100, 4, VIDE)

Ligne 7 : on récupère la Place de tête, on cherche son successeur et on lit l'élément qui s'y trouve : c'est donc 100.

10° On vous donne ci-dessous l'affectation d'une Liste générée en rajoutant des éléments au fur et à mesure à une Liste vide.

`1`	`lstA = ins(ins(ins(nLV(), 4, 0), 6, 0), 8, 0)`

Expliquer que le contenu de cette Liste soit (8, 6, 4, VIDE) en détaillant le fonctionnement en 3 étapes.
Fournir ensuite les instructions qui permettraient de passer de la Liste lstA contenant (8, 6, 4, VIDE) à une Liste lstB (10, 6, 4, VIDE)

Correction ?

...CORRECTION...

`1`	`lstA = ins(ins(ins(nLV(), 4, 0), 6, 0), 8, 0)`

Python exécute cette première fonction et on récupère donc une première liste contenant (4, VIDE) en position 0.

`1`	`lstA = ins(ins( (4, ), 6, 0), 8, 0)`

`1`	`lstA = ins(ins( (4, ), 6, 0), 8, 0)`

Python doit maintenant générer, à partir de (4, VIDE), une nouvelle liste où 6 est en position de tête (indice 0).

`1`	`lstA = ins( (6, 4), 8, 0)`

Il exécute et on récupère donc une liste contenant (6, 4, VIDE).

`1`	`lstA = ins( (6, 4), 8, 0)`

On voit qu'on doit maintenant rajouter à la liste (6, 4, VIDE) un élément 8 et se trouvant en place 0.

On obtient donc au final (8, 6, 4, VIDE).

Pour créer la liste B, il suffit de demander d'utiliser les primitives de cette façon&nbs:;

2
3

lstB = sup(lstA, 0)
lstA = ins(lstA, 10, 0)

1.7 Muable/Mutable ou immuable ?

Voir ?

Reconnaître un type Immuable via son prototype

Les primitives inserer() supprimer() d'une Liste immuable renvoie la référence d'une nouvelle Liste. Cela apparaît donc dans les signatures.

insT(lst:Liste, elt:Elément) → Liste NON VIDE
supT(lst:Liste NON VIDE) → Liste

Exemple d'utilisation :

...
...
...

lstA = nLV()
lstB = insT(lstA, 8)
lstC = supT(lstB)

Reconnaître un type Muable / Mutable via son prototype

On aurait également pu créer des primitives pour un type abstrait muable/mutable.

Dans ce cas, on ne renvoie pas une nouvelle structure, on modifie directement en mémoire les données de la liste fournie en entrée. On ne renvoie donc rien.

insT(lst:Liste, elt:Elément) → Vide
supT(lst:Liste NON VIDE) → Vide

Exemple d'utilisation :

...
...
...

lstA = nLV()
insT(lstA, 8)
supT(lstA)

On utilise souvent la sortie de sup() pour renvoyer l'élément qu'on vient de supprimer.

insT(lst:Liste, elt:Elément) → Vide
supT(lst:Liste NON VIDE) → Element supprimé

Exemple d'utilisation :

...
...
...

lstA = nLV()
insT(lstA, 8)
x = supT(lstA)

11° On suppose pour cette question qu'on dispose d'un type abstrait Liste muable / mutable. Que doit-on noter pour indiquer qu'on veut obtenir une modification de la Liste lstA contenant (10, 100) en (1, 10, 100) ?

lstA = inserer(lstA, 1, 0)
lstA = inserer(lstA, 0, 1)
inserer(lstA, 1, 0)
inserer(lstA, 0, 1)

Donner la bonne réponse et expliquer le problème engendré par les 3 autres propositions.

Pour rappel, voici le prototype de la fonction sur la version immuable :

inserer(lst:Liste, elt:Elément, i:Entier Naturel VALIDE) → Liste NON VIDE

Correction ?

...CORRECTION...

Les cas A et B sont nécessairement faux puisque la fonction inserer() ne renvoie rien dans le cas d'un type muable.

C'est donc C ou D.

Regardons le prototype :

inserer(lst, elt, i)

On veut insérer 1 en position 0, il faut donc faire cet appel :

inserer(lst, 1, 0)

La bonne réponse est donc C.

Avec D, on demande d'insérer un 0 en position 1.

Liste et LISP : un peu d'histoire...

Voir ?

LISP est le premier langage permettant de travailler à la fois en impératif et en fonctionnel.

Que veut dire LIPS ?

LIPS veut dire LISt Processing (traitement de listes en français).

C'est un langage fonctionnel : ces fonctions sont des fonctions pures qui ne peuvent travailler qu'avec les données immuables transmises par les paramètres : pas de variables globales par exemple.

Créé en 1958 par John McCarthy, l'un des fondateurs de l'intelligence artificiel, LISP reste l'un des langages fonctionnels les plus répandus et les plus simples. Il est utilisé à grande échelle dans le domaine de l'intelligence artificielle. LIPS est également particulièrement adapté à l'utilisation de la récursivité.

Dans les langages qui ont largement diffusé, on trouve dans l'ordre chronologique

le langage machine, puis
le langage d'assemblage, puis
FORTRAN et juste derrière
LISP (en 1958)

Le C ne viendra que plus tard (en 1972).

Python, encore plus tard (en 1991).

2 - Deux Listes en tant que type abstrait de données !

⇩ ⇧ ⤊

Pour aller plus loin et décrire plus précisément ce qu'est une Liste, il va falloir définir ... Place.

Comme pour les fonctions itératives et récursives, il existe deux grandes familles de Listes :

Les Listes itératives
Les Listes récursives

2.1 Liste itérative

Principe

La Liste itérative est une liste dans laquelle :

Les Places sont des cases qui ne "bougent" pas : elles possèdent un indice constant
les Eléments peuvent éventuellement changer de Place.

Voir

Idée sous-jacente : l'armoire avec des casiers fixes.

La Liste est l'armoire.
Les Places sont des casiers fixés dans la structure, sur lequel un numéro est inscrit définitivement
Les Eléments sont les choses qu'on place dans les casiers.

Dans la logique itérative, la fonction f() assemble elle-même les sous-réponses fournies par les autres fonctions a() b() c() qu'elle appelle.

Si on ramène cela au problème de la localisation des Places, cela donne la Liste Itérative : si on lui fournit un indice, la Liste peut localiser elle-même immédiatement la Place correspondante :

Cela ressemble énormément aux tableaux.

Avantage : facilité d'accès à un élément

Connaissant simplement un indice, on accède immédiatement à une Place et son Element.

Désavantage : insertion ou permutation plus long

Il est difficile d'effectuer des permutations de valeurs ou d'insérer une nouvelle donnée. Voici un exemple où on tente de produire (D, A, B, C) à partir de (A, B, C, D).

Les liaisons Liste-Places sont fixes mais on peut modifier l'association Place-Elément. On ne déplace donc pas les Places. mais on permute les Elements dans les Places.

On se rend compte que le nombre de déplacements est linéaire par rapport au nombre d'éléments dans la Liste.

C'est exactement l'analogie d'une armoire possèdant des casiers numérotés : on ne peut pas démonter le meuble pour bouger les casiers !

2.2 Liste récursive

Principe

La Liste récursive permet d'atteindre directement la tête. Les autres cases devant alors être localisées de proche en proche.

Depuis la Place de tête, on peut atteindre son successeur.
Depuis le successeur, on peut atteindre le successeur du successeur...
On peut modifier la Place vers laquelle pointe la Liste récursive pour indiquer où se trouve la tête.

Voir

Idée sous-jacente : le tiroir à dossier suspendus.

La Liste est le tiroir.
Les Places sont les dossiers suspendus, sans numérotation
Les Eléments sont les choses qu'on place dans les dossiers suspendus

Dans la logique récursive, la fonction délègue une partie des calculs à une autre fonction qui délègue elle-même le travail jusqu'à tomber sur une fonction "cas de base" qui pourra enfin répondre seule à une partie du problème. Les réponses remontent alors peu à peu jusqu'à la première fonction.

Si on ramène cela au problème de la localisation des Places, cela donne la Liste Récursive : cette fois, on ne peut accéder directement qu'à la Place de Tête. On peut accéder à toutes les autres places, mais il faudra les parcourir une à une puisque chaque Place est l'unique détentrice de l'identité de la Place suivante :

Désavantage : accès aux Places et Eléments plus long

Le nombre d'opérations nécessaire à la lecture de toute la Liste récursive est linéaire par rapport au nombre d'éléments dans la Liste puisqu'on part de la tête pour parcourir une à une toutes les Places.

Avantage : facilité d'insertion ou permutation

Il n'y pas de liaison imposée et constante entre Liste-Place. Chaque Place gère son successeur. Il suffit donc de modifier quelques liaisons de successeurs pour parvenir à modifier le déroulé de la séquence.

Si on étudie la modification, on se rend compte qu'on aura toujours que 3 modifications de liaisons à faire quelque soit le nombre d'éléments dans la Liste.

C'est exactement l'analogie d'un meuble à dossiers suspendus. On peut prendre un dossier et le mettre devant tous les autres sont avoir à bouger les autres dossiers.

2.3 Utilisation usuelle du mot "Liste"

Voir

Nous venons de passer plusieurs minutes à expliquer que l'idée abstrait Liste est en réalité trop vaste et qu'elle doit être précisée, soit via la Liste itérative, soit via la Liste récursive.

Ok.

En réalité, la plupart des gens utilisent

le mot tableau lorsqu'ils parlent d'une implémentation d'une liste itérative et
le mot liste pour désigner l'implémentation d'une liste récursive.

2.4 Et le type list de Python alors ?

Plusieurs choses à comprendre :

Le type list-Python n'est pas un type abstrait mais une implémentation.
La list-Python est une implémentation d'une Liste Itérative mutable .
Néanmoins, la list-Python est une amélioration de cette idée basique : on peut insérer en fin de liste avec la méthode append(), et supprimer en fin de liste avec la méthode pop().


>>> t = [10, 100, 6]
>>> t.append(1000)
>>> t
[10, 100, 6, 1000]
 
>>> t.pop()
1000
 
>>> t
[10, 100, 6]

La list-Python est donc l'implémentation d'une Liste Itérative possédant en apparence quelques fonctionnalités des Listes Récursives. Un savant mélange des deux.

3 - Liste récursive couple (Tête, Queue)

⇩ ⇧ ⤊

3.1 La Liste Récursive couple (Tête, Queue)

C'est une Liste Récursive IMMUABLE très simple : on accède, insère ou supprime uniquement au niveau de la tête de liste.

Voir ?

En réalité, on obtient donc une version très proche de la Liste de la partie 1 : celle où la Queue d'une Liste est fondamentalement une Liste elle-même.

3.2 Primitives de la Liste (Tête, Queue)

Voir ?

On donne les opérations primitives les plus basiques qui soient (sous entendu "il semble logique de pouvoir les implémenter par des fonctions ayant un coût constant").

L'accès, la lecture et la suppression se feront donc uniquement sur la Place de tête puisque c'est la seule directement accessible.

Les opérations primitives restreintes semblent donc différentes de celles d'une Liste classique. Voici les noms qu'on leur donne (ainsi que quelques alias plus courts à noter).

Fondamentales

nLV() ou nouvelleListeVide() → Liste VIDE

Exemple d'utilisation

lstA = nouvelleListeVide()
Le contenu de lstA est alors () par exemple.

estLV() ou estListeVide(lst:Liste) → Booléen

Exemple d'utilisation

lstA = nouvelleListeVide()
estListeVide(lstA) renvoie alors VRAI.

insT() ou insererTete(lst:Liste, elt:Elément) → Liste NON VIDE
cons()

La Liste est ici immuable puisqu'on renvoie une nouvelle Liste, plutôt que de juste modifier l'ancienne en mémoire.
Dans LISP, cette fonction se nomme cons() (comme construct).

Exemple d'utilisation

lstA = nouvelleListeVide()
lstB = insererTete(lstA, 5)
lstB contient alors (5, ()) qu'on pourrait noter simplement (5,).

lstB = insererTete(lstB, 15)
lstB contient alors quelque chose comme (15, (5, ())), qu'on peut plutôt représenter par (15, 5, vide) ou (15, 5).

Graphiquement, les relations entre les Places donnent alors ceci :

supT() ou supprimerTete(lst:Liste NON VIDE) → Liste
cdr()
queue()

Historiquement, dans LISP cette fonction se nomme cdr (contents of decrement register).
On pourrait égalemnet la nommer queue() puisque la liste qui est renvoyée est en réalité la queue de la liste fournie en l'entrée.

Exemple d'utilisation

On considère que lstB contient (25, (15, (5, ()))) ou (25, 15, 5)
lstC = supprimerTete(lstB)
lstC contiendra alors (15, (5, ())) ou (15, 5).
lstB contient toujours (25, (15, (5, ())))

Importante si on utilise les indices (ce qui n'est pas les cas avec les listes récursives)

~~longueur()~~

On décide de ne pas mettre longueur() ici car il faudrait d'autres informations que la simple localisation de la tête pour agir efficacement. Mais on pourra la construire à l'aide des autres primitives au besoin.

Interactions avec les Places

accT() ou accesTete(lst:Liste NON VIDE) → Place
tete()

On la nomme parfois tete() puisqu'elle renvoie la Place de tête.

contenu(plc:Place) → Elément

Exemple d'utilisation

On considère que lstB contient (25, (15, (5, ())))
ref = accesTete(lstB)
recup = contenu(ref)
recup contient alors 25. La liste lstB n'a pas été modifiée.

On aurait pu noter directement :
recup = contenu(accesTete(lstB))

succ() ou successeur(plc:Place) → Place|Vide

Exemple d'utilisation

On considère que lstB contient (25, (15, (5, ())))
ref = accesTete(lstB)
ref = successeur(ref)
ref = successeur(ref)
recup = contenu(ref)
On obtient alors la valeur 5 dans recup. La liste lstB n'a pas été modifiée.

Nous prendrons uniquement les 7 opérations primitives suivantes :

nLV() ou nouvelleListeVide() → Liste VIDE
estLV() ou estListeVide(lst:Liste) → Booléen
insT() ou insererTete(lst:Liste, elt:Elément) → Liste NON VIDE
supT() ou supprimerTete(lst:Liste NON VIDE) → Liste
tete() ou accesTete(lst:Liste NON VIDE) → Place
contenu(plc:Place) → Elément
succ() ou successeur(plc:Place) → Place|Vide

On remarquera que l'utilisateur ne crée jamais directement de Place : c'est la structure de données qui s'en charge lorsqu'on active insererTete().

La suite ?

Vous allez voir maintenant :

qu'on peut manipuler les données abstraites sans toucher un clavier
qu'on peut recréer les fonctionnalités manquantes de la Liste généraliste en utilisant ces 7 primitives
qu'il s'agit donc bien d'une Liste
qu'avec juste l'idée de cette Liste, on peut prévoir quelles actions seront rapides ou longues lorsqu'on réalisera l'implémentation réelle.

12° Donner le contenu des variables au fur et à mesure de l'exécution de cette suite d'actions. J'utilise une syntaxe Python en tant que pseudo-langage algorithmique.

lstA = insT(nLV(), 4)
lstB = insT(lstA, 6 )
lstC = insT(lstB, 0)
x = contenu(tete(lstC))
lstD = supT(lstC)
a = contenu(succ(tete(lstD)))

Attention, ce n'est pas un algorithme : un algorithme doit résoudre un problème ou répondre à une question. Ici, il ne s'agit que d'une suite d'actions.

Correction ?

...CORRECTION...

Ligne 1 : lstA contient (4, ()) ou (4,)

Ligne 2 : lstB contient (6, (4, ())) ou (6, 4)

Ligne 3 : lstC contient (0, (6, (4, ()))) ou (0, 6, 4)

Ligne 4 : x contient 0

Ligne 5 : lstD contient (6, (4, ())) ou (6, 4)

Ligne 6 : on récupère la zone de tête, on cherche son successeur et on lit l'élément qui s'y trouve : c'est donc 4.

PSEUDO-CODE

Pour les algorithmes de cette section, on utilisera du pseudo-code Python françisé mais en respectant globalement la façon de faire de Python (sans s'embêter avec les : en fin de déclaration par exemple).

L'appartenance à un bloc SI, POUR, TANT QUE ect... est signalée par

L'indentation en pseudo-Python
Le fait de ne pas avoir rencontré Fin POUR, Fin SI ect... en pseudo-langage classique.

L'affectation est signalée par

Le symbole = en pseudo-Python
La flèche ← en pseudo-langage classique.

RENVOYER x plutôt que return x
NON plutôt que not
POUR i variant de 0 à 10 plutôt que for i in range(11):
|
|
Fin POUR
POUR chaque valeur v du tableau t plutôt que for v in t:
|
|
Fin POUR
TANT QUE v est différent de a plutôt que while v != a:
|
|
Fin TANT QUE
SI-SINON SI-SINON qui remplaceront les if-elif-else
|
|
Fin SI

13° Deux questions.

Question 13.a

Réaliser l'algorithme premier() qui correspond au fait de récupérer la valeur de la tête directement, plutôt que de devoir utiliser et taper deux primitives.

ALGORITHME premier(lst:Liste NON VIDE) → Elément

ENTREE : lst, une Liste NON VIDE

SORTIE : l'Elément contenu dans la tête

Question 13.b

Si on suppose que les primitives contenu() et tete() seront implémentables par des fonctions à coût constant, que pouvez-vous dire du coût supposé de la fonction premier() une fois implémentée ?

Correction ?

...CORRECTION...

ALGORITHME de premier(lst:Liste NON VIDE) → Elément

RENVOYER contenu(accesTete(lst))

Coût futur expliqué avec les notations asymptotiques

𝞗(1+1+1)

= 𝞗(1)

Coût CONSTANT

Coût futur expliqué avec des phrases

Si accesTete() est coût constant, si contenu() est à coût constant, il ne faudra que deux actions à coût constant et un retour à coût constant.

Trois actions à coût constant donc l'algorithme est à coût constant.

14-A° Comment traduire ce test en français ?

SI (NON estListeVide(lst))

Correction ?

...CORRECTION...

Traduction mot à mot : on veut agir si la liste est NON VIDE.

Traduciton : on veut agir si la liste n'est pas vide, c'est à dire si elle contient au moins un élément.

14-B° Quelle est l'expression équivalente à celle de la question précédente :

SI NON estListeVide(lst)

SINON estListeVide(lst)

Correction ?

...CORRECTION...

SI NON estListeVide(lst)

On agit ici si la liste est NON VIDE.

L'opérateur NON a priorité plus forte que le SI : c'est donc comme si on avait mis les parenthèses :

SI (NON estListeVide(lst))

SINON estListeVide(lst)

Ici, c'est totalement différente. Il s'agit de l'idée abstraite du elif de Python.

On dit donc ici d'agir sinon si la liste est VIDE !

15° Deux questions.

Question 15.a

Fournir les actions de l'algorithme longueur() ci-dessous, qui correspond au fait de récupérer le nombre d'éléments dans la Liste. Il faudra utiliser une version itérative utilisant un TANT QUE.

ALGORITHME longueur(lst:Liste) → Entier Naturel

ENTREE : lst, une Liste (attention, elle pourrait être vide, aucune précondition autre que le type)

SORTIE : le nombre d'éléments contenus dans lst

POSTCONDITION :lst est inchangé puisqu'on décide de travailler sur un type Liste immuable.

Question 15.b

Si on suppose que les 7 primitives de base devraient être implémentables par des fonctions à coût constant, que pouvez-vous dire du coût supposé de la fonction longueur() une fois implémentée ?

Question 15.c

Après avoir regardé ma correction, un élève pense que la liste est modifiée. Expliquez lui pourquoi il se trompe.

Correction ?

...CORRECTION...

ALGORITHME longueur(lst:Liste) → Entier Naturel

nb ← 0

TANT QUE NON estListeVide(lst)

nb ← nb + 1

lst ← supprimerTete(lst)

Fin du TANT QUE

RENVOYER nb

Coût futur expliqué avec les notations asymptotiques

𝞗(1 + 3*n + 1)

= 𝞗(3*n)

= 𝞗(n), donc linéaire en n.

Coût futur expliqué avec des phrases :

On a une première affectation simple à coût constant 𝞗(1).
On réalise la boucle n fois (puisqu'il faut couper n têtes) et lors de cette boucle, on réalise 3 actions à coût constant (une primitive, une incrémentation et une autre primitive). On a donc du 𝞗(n*3) et donc du linéaire.
On renvoie la réponse à coût constant 𝞗(1)

On ne garde que le coût le plus important : l'algorithme est donc linéaire.

Pour la question C, il suffit de signaler que lorsqu'on écrit lst ← supprimerTete(lst), cela veut dire qu'on stocke la nouvelle liste supprimerTete(lst) dans une nouvelle variable locale : elle porte le même nom mais désigne bien une autre donnée que la liste reçue initialement.

16° Réaliser l'algorithme longueur() en utilisant cette fois une version récursive.

Pour cela, demandez-vous

Pour quel cas de base un appel de la fonction pourra répondre seule ?
Que devra faire la fonction qui s'occupe d'une Place une fois qu'elle aura reçu la réponse du successeur ?

ALGORITHME longueur(lst:Liste) → Entier Naturel

ENTREE : lst, une Liste (attention, elle pourrait être vide, aucune précondition autre que le type)

SORTIE : le nombre d'éléments contenus dans lst

On rappelle qu'on a décidé de travailler sur un type Liste immuable.

Correction ?

...CORRECTION...

Le principe général est de considèrer qu'une Liste dit que sa longueur est 0 si elle est vide et que sinon, la fonction répondra 1 + la réponse de la queue de la liste.

ALGORITHME longueur(lst:Liste) → Entier Naturel

SI estListeVide(lst)

RENVOYER 0

SINON

RENVOYER 1 + longueur(supprimerTete(lst))

Fin du SI

Dans la suite des exercices, on considère donc qu'on peut désormais utiliser ces deux fonctions.

premier(lst:Liste NON VIDE) → Elément
longueur(lst:Liste) → Entier Naturel

17° Trouver l'algorithme de inverser(), qui doit renvoyer une nouvelle Liste où tous les éléments sont inversés : le dernier est le premier, l'avant-dernier est le deuxième...

ALGORITHME inverser(lst:Liste) → Liste

DESCRIPTION : renvoie une nouvelle Liste où l'ordre des éléments est inversé par rapport à lst.

POSTCONDITION : la Liste renvoyée à la même longueur que lst et lst est inchangée.

Si on envoie (5, 15, 100, 1), on doit recevoir (1, 100, 15, 5).

Vous pouvez utiliser les opérations primitives ainsi que longueur(), et premier().

Evaluer ensuite son coût supposé après implémentation.

Correction ?

...CORRECTION...

ALGORITHME inverser(lst:Liste) → Liste

lst_inverse ← nouvelleListeVide()

TANT QUE NON estListeVide(lst)

element ← premier(lst)

lst ← supprimerTete(lst)

lst_inverse ← insererTete(lst_inverse, element)

Fin du TANT QUE

RENVOYER lst_inverse

Une version avec une boucle bornée POUR est bien entendu possible : il suffit de lancer un appel à longueur() pour connaître le nombre de tours de boucle à faire.

Coût futur expliqué avec les notations asymptotiques

𝞗(1 + 4*n + 1)

= 𝞗(4*n)

= 𝞗(n), donc linéaire en n.

Coût futur expliqué avec des phrases

On a un appel à une primitive, donc à coût constant.

Pour la boucle, on aura 4 opérations à coût constant par tour de boucle. Or, on va réaliser un nombre de tour de boucle qui dépend de la longueur de la liste initiale. On a donc un coût linéaire puisqu'on fait autant n fois des actions à temps constant.

Le coût final est donc linéaire.

18-A° Le but de cette question en trois parties est de créer la fonction inserer() avec gestion de l'indice pour savoir où réaliser l'insertion (équivalent à la notation [i] en Python).

Vous pouvez utiliser les 7 primitives ainsi que premier()

ALGORITHME inserer(lst:Liste, elt:Elément, i:Entier Naturel VALIDE) → Liste NON VIDE

DESCRIPTION : Renvoie une nouvelle Liste comportant le nouvel élément à la position indiquée par l'indice fourni. Certains emplacements sont donc décalés d'une position par rapport à la Liste initiale.

Pour insérer comme nouvelle Tête, on doit donc envoyer i valant 0.
Pour insérer comme nouvelle fin, on doit envoyer longueur qui correspond à un indice "vide" pour la liste de départ.
Pour insérer juste avant la fin, on doit envoyer longueur -1. Cela doit avoir comme conséquence de pousser la fin en position longueur.

PRECONDITIONS : l'indice i caractérise une indice valide pour l'insertion et elt doit avoir un type compatible avec le reste des Eléments si la Liste est homogène.

POSTCONDITION : la Liste renvoyée possède un emplacement en plus mais lst est inchangée.

Exemples d'utilisation

lstA = nouvelleListeVide()
lstB = inserer(lstA, 5, 0)
lstB contient alors (5, () ) qu'on pourrait noter simplement (5, vide).

lstC = inserer(lstB, 15, 0)
lstC contient alors (15, (5, () )) qu'on pourrait noter (15, 5, vide).

lstD = inserer(lstC, 25, 1)
lstD contient alors (15, (25, (5, () ))) qu'on pourrait noter (15, 25, 5, vide).

lstE = inserer(lstD, 50, 3)
lstE contient alors (15, (25, (5, (50, () )))) qu'on pourrait noter (15, 25, 5, 50, vide).

Correction ?

...CORRECTION...

ALGORITHME inserer(lst:Liste, elt:Elément, i:Entier Naturel VALIDE) → Liste NON VIDE

/// Etape 1 : on supprime et mémorise les i premières têtes

memoire ← nouvelleListeVide()

POUR k variant de 0 à (i - 1) . . . . . . . . . . on fait la boucle i fois

element ← premier(lst) . . . . . . . . on lit la 1er valeur de lst

lst ← supprimerTete(lst) . . . . . . . . . . on supprime la tête

memoire ← insererTete(memoire, element) . . . . on rajoute en mémoire

Fin du POUR

/// Etape 2 : on insère le nouvel élément

lst ← insererTete(lst, elt)

/// Etape 3 : on replace les i éléments supprimés

POUR k variant de 0 à (i - 1) . . . . . . . . on fait la boucle i fois

element ← premier(memoire) . . . . . . on lit la 1er valeur en mémoire

memoire ← supprimerTete(memoire) . . . . . on supprime la tête

lst ← insererTete(lst, element) . . . . . . . on rajoute dans lst

Fin du POUR

RENVOYER lst

18-B° Passons à une fonction presque similaire au niveau de l'algorithme :

ALGORITHME supprimer(lst:Liste NON VIDE, i:Entier Naturel VALIDE) → Liste

DESCRIPTION : Renvoie une nouvelle Liste dans laquelle on a supprimé l'ancien emplacement ayant cet indice. Certains emplacements sont donc décalés d'une position par rapport à la Liste initiale.

Pour supprimer l'élément de Tête, on doit donc envoyer i valant 0.
Pour supprimer l'élément de fin, on doit envoyer longueur -1.

PRECONDITION : l'indice i est un indice valide, la Liste reçue doit être NON VIDE.

POSTCONDITION : la Liste renvoyée possède un emplacement en moins mais lst est inchangée.

Exemple d'utilisation

Partons de lstE contenant (15, (25, (5, (50, () )))) ou simplement (15, 25, 5, 50, ).
lstF = supprimer(lstE, 1)
lstF contient alors (15, (5, (50, () ))) ou simplement (15, 5, 50, ).

lstG = supprimer(lstF, 2)
lstG contient alors (15, (5, () )) ou simplement (15, 5, ).

Correction ?

...CORRECTION...

Pour cet algorithme, il n'y a que l'étape 2 qui change par rapport à l'insertion : on supprime une tête en plus plutôt que d'en insérer une nouvelle.

ALGORITHME supprimer(lst:Liste NON VIDE, i:Entier Naturel VALIDE) → Liste

/// Etape 1 : on supprime et mémorise les i premières têtes

memoire ← nouvelleListeVide()

POUR k variant de 0 à (i - 1) . . . . . . . . . . on fait la boucle i fois

element ← premier(lst) . . . . . . . . on lit la 1er valeur de lst

lst ← supprimerTete(lst) . . . . . . . . . . on supprime la tête

memoire ← insererTete(memoire, element) . . . . on rajoute en mémoire

Fin du POUR

/// Etape 2 : on insère le nouvel élément

lst ← supprimerTete(lst)

/// Etape 3 : on replace les i éléments supprimés

POUR k variant de 0 à (i - 1) . . . . . . . . on fait la boucle i fois

element ← premier(memoire) . . . . . . on lit la 1er valeur en mémoire

memoire ← supprimerTete(memoire) . . . . . on supprime la tête

lst ← insererTete(lst, element) . . . . . . . on rajoute dans lst

Fin du POUR

RENVOYER lst

18-C° Estimer le coût des deux fonctions une fois qu'elles seront correctement implémentées dans un langage de programmation.

Correction ?

...CORRECTION...

Futur coût expliqué avec les notations asymptotiques

Si on cumule les coûts des phases 1, 2 et 3, on obtient

𝞗(1 + i*3 + 1 + i*3 + i) =
𝞗(3 + 6*i) =
𝞗(6*i) =
𝞗(i) = 𝓞(n)

Explication du passage de i à n : puisqu'on a montré que l'algorithme est exactement linéaire en i, et que i ≤ n, on a le droit de noter que l'algorithme à un coût inférieur à un coût linéaire en n puisque i est compris entre 0 et n.

Futur coût expliqué avec des phrases

Phase 1

Créer une nouvelle Liste VIDE est à coût constant (noté 1).
Supprimer et mémoriser i têtes consiste à faire i fois 3 opérations à coût constant (noté 3*i). C'est donc linéaire en i.

Phase 2

Insérer ou supprimer une tête supplémentaire est à coût constant (noté 1).

Phase 3

Remettre en place les i têtes précédentes consiste à faire i fois 3 opérations à coût constant (noté 3*i). C'est donc linéaire par rapport à i.
Renvoyer la nouvelle liste est à coût constant (noté 1).

Pour l'analyse asymptotique du coût, on garde uniquement le coût le plus important, soit ici un coût linéaire sur i.

i peut avoir comme valeur (n-1) dans le pire des cas, on en déduit que le coût est également coût linéaire sur n.

19° Réaliser un algorithme ieme() qui ramène l'élément placé en position i d'une Liste NON VIDE. L'autre précondition est que l'indice fourni soit valide pour cette liste.

ALGORITHME ieme(lst:Liste NON VIDE, i:Entier Naturel VALIDE) -> Element

Correction ?

...CORRECTION...

Le principe est de supprimer i têtes.

Pas la peine de stocker, la liste est IMMUABLE : on ne coupe donc pas vraiment la liste de base.

Il suffit ensuite de renvoyer le premier élément de la liste obtenue.

/// Etape 1 : on supprime i têtes

POUR k variant de 0 à (i - 1)

lst ← supprimerTete(lst)

Fin POUR

/// Etape 2 : on renvoie le premier

RENVOYER premier(lst)

20° Réaliser un algorithme recherche() qui renvoie l'indice du premier élément ayant la bonne valeur présent dans une Liste NON VIDE. Si l'élément n'est pas présent, la fonction renvoie -1.

ALGORITHME recherche(lst:Liste, x:Elément) -> Entier

Correction ?

...CORRECTION...

4 - Implémentation

⇩ ⇧ ⤊

4.1 Vocabulaire retenu sur ce site

un algorithme manipule des types abstraits de données (c'est la phase de conception théorique)
le passage de l'idée abstraite à sa réalisation concrète en machine se nomme l'implémentation.
un programme manipule des types (implémentés) (c'est la phase de réalisation pratique).

ALGORITHME ⇒ Implémentation ⇒ PROGRAMME

TYPE ABSTRAIT ⇒ Implémentation ⇒ TYPE (implémenté)

Type abstrait de données une idée abstraite mais précise de la façon de traiter les données. On trouve souvent l'acronyme TAD.
Type : l'implémentation en machine d'une donnée. Cela regroupe donc les types simples et les types construits.
Type simple : l'implémentation en machine d'une donnée unique, comme un entier, un flottant...
Type construit, type structuré : l'implémentation en machine d'une donnée se comportant comme un conteneur : elle contient d'autres données.

D'où le nom de la fonction native Python type().

Une structure de données est le nom qu'on donne à l'ensemble d'un type associé aux fonctions qu'on peut appliquer aux données stockées.

4.2 Implémentation de certains types abstraits en Python

Selon les langages, certains types abstraits sont déjà implémentés efficacement en pratique. Le langage de programmation possède alors déjà des types natifs permettant de les utiliser.

Par exemple, en Python :

On gère le type abstrait booléen en utilisant le type natif bool.
On gère le type abstrait entier en utilisant le type natif int.
On gère le type abstrait nombre à virgule en utilisant le type natif float.
Donc tous les nombres réels ne seront pas réellement tous bien enregistrés.
On gère le type abstrait tableau statique (array en anglais) en utilisant le type natif ... list.
On gère le type abstrait tableau dynamique (vector en anglais) en utilisant le type natif list.
On gère le type abstrait tableau associatif en utilisant le type natif dict.
On gère le type abstrait p-uplet nommé en utilisant le type natif dict.
On gère le type abstrait p-uplet en utilisant le type natif tuple.
On gère le type abstrait ensemble en utilisant le type natif set.

🏠 TRAVAIL PERSONNEL° Réaliser les exercices supplémentaires Maison (voir le lien) en rédigeant correctement vos réponses.

Exercices

5 - FAQ

⇩ ⇧ ⤊

C'est quoi le coût déjà ?

Voir

Après deux mois de vacances, il est possible que vos souvenirs soient plutôt flous. Les rappels de cours ci-dessous vous permettront de vous y retrouver.

(Rappel).1 - Introduction à la notion de coût d'un algorithme

Voir

Définition

Le coût d'un algorithme exprime la façon dont l'algorithme réagit globalement à l'augmentation du nombre n de données à traiter.

On évalue souvent le coût dans le pire des cas car il borne le comportement de l'algorithme : s'il se comporte bien dans le pire des cas, c'est qu'à priori nous allons pouvoir l'utiliser.

PROBLEMES FACILES

Facile veut dire qu'on peut utiliser un programme qui fournira la réponse en un temps raisonnable.

Coût constant (noté 1 ou CST)

Si n*2 alors op inchangé

Si on modifie le nombre n de données, le nombre d'opérations élémentaires op reste le même.

Exemple

Avec n = 6 données, on a besoin de op = 5 opérations élémentaires.
Si n*2 (n = 12), alors op = 5.
Si n*4 (n = 24), alors op = 5.
Si n*8 (n = 48), alors op = 5.

C'est donc pas mal !

Les coûts logarithmiques (notés log_k(n)

si n*k alors op+1

Si on multiple par k le nombre n de données, alors on augmente juste op de 1.

Plus k est grand, plus l'algorithme va être rapide. Quelques exemples où le coût devient de moins en moins bon :

log₁₀ : n*10 alors op+1. Celui-ci est souvent utilisé en physique-chimie.
log₃ : n*3 alors op+1
log_e ou juste ln : n*e alors op+1. e est la constante de Néper qui vaut approximativement 2,71. Ce logarithme particulier se nomme d'ailleurs le logarithme népérien.
log₂ ou juste lg : n*2 alors op+1. C'est celui qu'on rencontre le plus souvent en informatique.

dont le coût logarithmique base 2 (noté log₂(n) ou lg(n) )

si n*2 alors op+1

Si on multiple par 2 le nombre n de données, alors on augmente juste op de 1.

De façon plus détaillée,

si n est multiplié par 2, alors on augmente juste op de 1;
si n est multiplié par 4, alors on augmente juste op de 2;
si n est multiplié par 8, alors on augmente juste op de 3;
...

Exemple

Avec n=6 données, on a besoin de op=5 opérations élémentaires.
Si n*2 (12 données), on aura op+1 soit 5+1=6 opérations.
Si n*4 (24 données), on aura op+2 soit 5+2=7 opérations.
Si n*8 (48 données), on aura op+3 soit 5+3=8 opérations.

Ce coût se situe donc entre CONSTANT et LINEAIRE.

Les coûts polynomiaux (notés n^k)

Si n*2 alors op*constante (on notera que la constance vaut 2^k)

Si on multiple par 2 le nombre n de données, on multiple par la constante 2^k le nombre op d'opérations élémentaires.

Plus k est grand, plus l'algorithme va être lent. Quelques exemples où le coût devient de moins en moins bon :

n¹ : n*2 alors op*2 : le coût linéaire.
n² : n*2 alors op*2² : le coût quadratique.
n³ : n*2 alors op*2³ : le coût cubique.

dont le coût linéaire (noté n)

Si n*2 alors op*2

Si on double le nombre n de données, on double le nombre op d'opérations élémentaires.

De façon plus mathématique,

si n est multiplié par 2, alors on multiple op par 2;
si n est multiplié par 3, alors on multiple op par 3;
si n est multiplié par 4, alors on multiple op par 4
...

Exemple

Avec n=6 données, on a besoin de op=5 opérations élémentaires.
Si n*2 (12 données), on aura op*2 soit 5*2=10 opérations.
Si n*4 (24 données), on aura op*4 soit 5*4=20 opérations.
Si n*8 (48 données), on aura op*8 soit 5*8=40 opérations.

C'est un peu plus long que du coût constant.

dont le coût quadratique (noté n²)

Si n*2 alors op*(2²)

Si on double le nombre n de données, on quadruple le nombre op d'opérations élémentaires.

De façon plus mathématique,

si n est multiplié par 2, alors on multiple op par 2²;
si n est multiplié par 3, alors on multiple op par 3²;
si n est multiplié par 4, alors on multiple op par 4²
...

Exemple

Avec n=6 données, on a besoin de op=5 opérations élémentaires.
Si n*2 (12 données), on aura op*2² soit 5*4=20 opérations.
Si n*4 (24 données), on aura op*4² soit 5*16=80 opérations.
Si n*8 (48 données), on aura op*8² soit 5*64=320 opérations.

Cela devient réellement de plus en plus grand lorsque les données deviennent importantes.

et tous les autres coûts polynomiaux (notés n^k)

Si n*2 alors op*(2^k)

Si on double le nombre n de données, on multiplie par la constante 2^k le nombre op d'opérations élémentaires.

De façon plus mathématique,

si n est multiplié par 2, alors on multiple op par 2^k;
si n est multiplié par 3, alors on multiple op par 3^k;
si n est multiplié par 4, alors on multiple op par 4^k
...

PROBLEMES DIFFICILES

Difficile veut dire qu'on peut utiliser un programme mais qu'il fournira la réponse en un temps déraisonnable lorsque le nombre de données n deviendra grand.

Coût exponentiel (noté kⁿ)

Si n*2 alors op*(kⁿ), ou encore si n+1 alors op*k

Si on double le nombre n de données, on multiplie par kⁿ le nombre op d'opérations élémentaires. Notez bien que le facteur multiplicatif n'est donc plus une constante par rapport à n.

Cela veut également dire que si on augmente juste de 1 le nombre n de données, on multiplie par k le nombre op d'opérations élémentaires.

Plus k est grand, plus l'algorithme va être lent.. Quelque exemples où le coût devient de moins en moins bon :

2ⁿ : n+1 alors op*2. L'exponentielle base 2 est rencontrée assez souvent en informatique.
eⁿ : n+1 alors op*e. e est la constante de Néper qui vaut approximativement 2,71. Cette fonction exponentielle particulière se nomme juste "fonction exponentielle".
3ⁿ : n+1 alors le op*3. L'exponentielle base 3.
10ⁿ : n+1 alors le op*10. L'exponentielle base 10.

dont l'exponentielle base 2 (noté 2ⁿ)

Si n*2 alors op*(2ⁿ), ou encore si n+1 alors op*2

Si on double le nombre n de données, on multiplie par 2ⁿ le nombre op d'opérations élémentaires. Notez bien que le facteur multiplicatif n'est donc plus une constante par rapport à n.

Cela veut également dire que si on augmente juste de 1 le nombre n de données, on multiplie par 2 le nombre op d'opérations élémentaires.

Exemple 1 où on augmente les données de 1 à la fois

Avec n=1 données, on a besoin de op=5 opérations élémentaires.
Si on passe de 1 à 2 données (n+1 avec n=1), on aura op*2 soit 5*2=10 opérations.
Si on passe de 2 à 3 données (n+1 avec n=2), on aura op*2 soit 10*2=20 opérations.
Si on passe de 3 à 4 données (n+1 avec n=3), on aura op*2 soit 20*2=40 opérations.
Si on passe de 4 à 5 données (n+1 avec n=4), on aura op*2 soit 40*2=80 opérations.

Exemple 2 où on double les données :

Avec n=6 données, on a besoin de op=5 opérations élémentaires.
Si on passe de 6 à 12 données (n*2 avec n=6), on aura op*2ⁿ soit 5*2⁶=5*64=320 opérations.
Si on passe de 12 à 24 données (n*2 avec n=12), on aura op*2ⁿ soit 320*2¹²=320*4096=1310720 opérations.

On voit bien qu'avec une évolution exponentielle (même base 2, la moins "grave"), on perd rapidement la possibilité de réaliser tous les calculs nécessaires :


>>> 2**100
1267650600228229401496703205376
>>> 2**1000
10715086071862673209484250490600018105614048117055336074437503883703510511249361224931983788156958581275946729175531468251871452856923140435984577574698574803934567774824230985421074605062371141877954182153046474983581941267398767559165543946077062914571196477686542167660429831652624386837205668069376

On notera bien que n est en position d'exposant.

Coût factoriel (noté n!)

Si n*2 alors plus que op*((n+1)ⁿ) opérations car op dépend de n!= n*(n-1)*(n-2)*...*3*2*1.

Par définition, la factorielle de n vaut n*(n-1)*(n-2)*...*3*2*1.

Lorsqu'on double le nombre de données, on passe donc de n! à (2n)!.

Cela veut dire qu'on prend le nombre d'opérations nécessaires pour n! et qu'on les multiplie par (n+1)*(n+2)*(n+3)*...*(n+n).

On a donc n multiciplication à faire par des facteurs qui sont tous plus grand que n.

On doit donc multiplier le nombre d'opérations par un facteur plus grand que nⁿ. C'est donc encore pire que le coût exponentiel.

Exemple

Avec n = 1 donnée, n! = 1 = 1.
Avec 2, n! = 1*2 = 2.
Avec 3, n! = 1*2*3 = 6.
Avec 4, n! = 1*2*3*4 = 24.
Avec 5, n! = 1*2*3*4*5 = 120.
Avec 6, n! = 1*2*3*4*5*6 = 720.
Avec 7, n! = 1*2*3*4*5*6*7 = 5040.
Avec 8, n! = 1*2*3*4*5*6*7*8 = 40320.

On pourrait croire que cela évolue moins vite que l'exponentiel mais dès que n devient grand, cela explose encore plus vite que le coût exponentiel.


>>> import math
>>> math.factorial(100)
93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000
>>> math.factorial(1000)
402387260077093773543702433923003985719374864210714632543799910429938512398629020592044208486969404800479988610197196058631666872994808558901323829669944590997424504087073759918823627727188732519779505950995276120874975462497043601418278094646496291056393887437886487337119181045825783647849977012476632889835955735432513185323958463075557409114262417474349347553428646576611667797396668820291207379143853719588249808126867838374559731746136085379534524221586593201928090878297308431392844403281231558611036976801357304216168747609675871348312025478589320767169132448426236131412508780208000261683151027341827977704784635868170164365024153691398281264810213092761244896359928705114964975419909342221566832572080821333186116811553615836546984046708975602900950537616475847728421889679646244945160765353408198901385442487984959953319101723355556602139450399736280750137837615307127761926849034352625200015888535147331611702103968175921510907788019393178114194545257223865541461062892187960223838971476088506276862967146674697562911234082439208160153780889893964518263243671616762179168909779911903754031274622289988005195444414282012187361745992642956581746628302955570299024324153181617210465832036786906117260158783520751516284225540265170483304226143974286933061690897968482590125458327168226458066526769958652682272807075781391858178889652208164348344825993266043367660176999612831860788386150279465955131156552036093988180612138558600301435694527224206344631797460594682573103790084024432438465657245014402821885252470935190620929023136493273497565513958720559654228749774011413346962715422845862377387538230483865688976461927383814900140767310446640259899490222221765904339901886018566526485061799702356193897017860040811889729918311021171229845901641921068884387121855646124960798722908519296819372388642614839657382291123125024186649353143970137428531926649875337218940694281434118520158014123344828015051399694290153483077644569099073152433278288269864602789864321139083506217095002597389863554277196742822248757586765752344220207573630569498825087968928162753848863396909959826280956121450994871701244516461260379029309120889086942028510640182154399457156805941872748998094254742173582401063677404595741785160829230135358081840096996372524230560855903700624271243416909004153690105933983835777939410970027753472000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000

PROBLEMES INDECIDABLES

Notez bien que les problèmes faciles et difficiles sont décidables (le programme finira toujours par fournir une réponse si on lui laisse le temps).

Il existe des problèmes encore plus complexes :: les problèmes indécidables. Sur ces problèmes, l'ordinateur répond parfois mais par sur une infinité de calculs sur d'autres entrées. Et dans ce cas, il ne pourra jamais vous répondre.

(Rappel).2 - coût : combiner différentes parties de l'algorithme

Voir

A - Principe

Rechercher un coût revient à se demander l'allure de la fonction qui simule le nombre d'opérations fondamentales à réaliser pour répondre au problème lorsque les données n augmentent.

On parle de coût asymptotique car on se demande ce qui se passe lorsque n devient asymptotiquement grande.

Lorsqu'on est confronté à un algorithme qui possède plusieurs phases ayant chacune son propre coût, comment faire ?

Facile.

On prend le coût le moins favorable.

B - Exemple

Considérons un algorithme composé :

D'une première partie composée de 4 actions à coût constant : 4*1.
D'un deuxième partie composée d'un boucle dont le coût est 2*n³.
D'une dernière partie dont le coût est quadratique en 10*n².

Si on ajoute les trois, cela donne 4*1 + 2*n³ + 10*n².

On ne garde que le coût le plus défavorable : 2*n³.

On supprime le facteur constant : n³.

Le coût de cet algorithme est donc un coût cubique.

(Rappel).3 - Définition simplifiée de la notation 𝓞 : borne supérieure du coût de l'algorithme

Voir

Cette notation se note GRAND O.

Parfois, on ne peut pas trouver le comportement exact d'un algorithme. Son comportement peut être très variable en fonction des entrées fournies par exemple.

Cette notation indique que dans le pire des cas, l'algorithme aura ce coût.

On obtient donc une indication similaire à "inférieur ou égal" vis à vis des complexités.

Exemple n°1 :

𝓞(n²) veut dire que notre algorithme se comporte peut-être en n², ou en n, ou en log₂(n) ou même en 1.

Le coût est inférieur ou égal à un coût quadratique.

Exemple n°2 :

𝓞(n⁴) veut dire que notre algorithme se comporte peut-être en n⁴, ou en n³, ou moins encore.

Le coût est inférieur ou égal à un coût polynomial en n⁴.

Exemple n°3 :

𝓞(n) veut dire que notre algorithme se comporte peut-être en n, ou en n^1/2 ou n, ou en log₂(n) ou en moins encore.

Le coût est inférieur ou égal à un coût linéaire.

Exemple n°4 :

𝓞(2ⁿ) veut dire que notre algorithme se comporte peut-être en n⁴, ou en n³ ou moins encore.

Le coût est inférieur ou égal à un coût exponentiel (puissance de 2 ici).

(Rappel).4 - Définition simplifiée de la notation 𝞗 : comportement exact de l'algorithme

Voir

Cette notation se note THETA.

Pour comparer les complexités des algorithmes entre eux, on utilise la notation suivante par exemple :

f(n) = 𝞗(n²) indique que la fonction f(n) se comporte d'une façon similaire à n² pour les grandes valeurs de n.

On obtient une indication un peu similaire à "se comporte toujours comme" vis à vis des complexités.

Exemple n°1

Si f(n) = 4 n² + 100 n + 6, on doit écrire f(n) = 𝞗(n²) uniquement.

Exemple n°1

Si f(n) = 12 n³ - 500 n + 10000, on doit écrire f(n) = 𝞗(n³) uniquement.

Le principe est donc de ne garder que l'allure la plus rapide et de négliger tous les facteurs constants.

Activité publiée le 21 09 2020
Dernière modification : 18 09 2024
Auteur : ows. h.

⏪

⏫

⏩

11 - type abstrait de données Liste

1 - La Liste en tant que type abstrait de données

1.1 1er partie de la définition de Liste : l'idée générale

A - Propriétés générales d'organisation

B - Vocabulaire

C - Exemple

1.2 Représentations d'une Liste

A - Représentation graphique Tête → Queue

B - Définition (en français)

C - Définition formelle (en mathématique)

D - Représentations : imbrication ou séquence ordonnée

E - Représentation de la liste VIDE

1.3 Signatures et erreur de Type

A - Signature : définition

B - Signature non valide : erreur de Type

C - Signature valide

1.4 Spécification d'une fonction

1.5 Opérations primitives

1.6 2nd partie de la définition de Liste : spécifications des primitives

A - Dépendances du type abstrait Liste

B - Spécifications : définition

Résumé : les 8 types de primitives qu'il faudra avoir ou reconstruire à partir des autres :

1.7 Muable/Mutable ou immuable ?

Reconnaître un type Immuable via son prototype

Reconnaître un type Muable / Mutable via son prototype

2 - Deux Listes en tant que type abstrait de données !

2.1 Liste itérative

Principe

Avantage : facilité d'accès à un élément

Désavantage : insertion ou permutation plus long

2.2 Liste récursive

Principe

Désavantage : accès aux Places et Eléments plus long

Avantage : facilité d'insertion ou permutation

2.3 Utilisation usuelle du mot "Liste"

2.4 Et le type list de Python alors ?

3 - Liste récursive couple (Tête, Queue)

3.1 La Liste Récursive couple (Tête, Queue)

3.2 Primitives de la Liste (Tête, Queue)

PSEUDO-CODE

4 - Implémentation

4.1 Vocabulaire retenu sur ce site

4.2 Implémentation de certains types abstraits en Python

5 - FAQ

C'est quoi le coût déjà ?

(Rappel).1 - Introduction à la notion de coût d'un algorithme

Définition

Coût constant (noté 1 ou CST)

Les coûts logarithmiques (notés logk(n)

dont le coût logarithmique base 2 (noté log2(n) ou lg(n) )

Les coûts polynomiaux (notés nk)

dont le coût linéaire (noté n)

dont le coût quadratique (noté n2)

et tous les autres coûts polynomiaux (notés nk)

Coût exponentiel (noté kn)

dont l'exponentielle base 2 (noté 2n)

Coût factoriel (noté n!)

(Rappel).2 - coût : combiner différentes parties de l'algorithme

A - Principe

B - Exemple

(Rappel).3 - Définition simplifiée de la notation 𝓞 : borne supérieure du coût de l'algorithme

(Rappel).4 - Définition simplifiée de la notation 𝞗 : comportement exact de l'algorithme

Les coûts logarithmiques (notés log_k(n)

dont le coût logarithmique base 2 (noté log₂(n) ou lg(n) )

Les coûts polynomiaux (notés n^k)

dont le coût quadratique (noté n²)

et tous les autres coûts polynomiaux (notés n^k)

Coût exponentiel (noté kⁿ)

dont l'exponentielle base 2 (noté 2ⁿ)