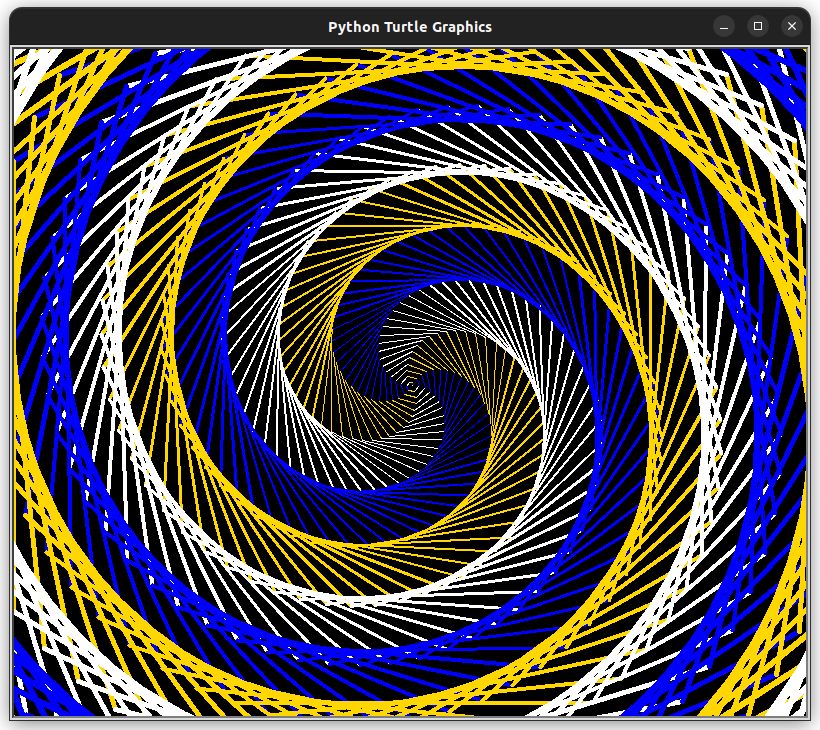
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
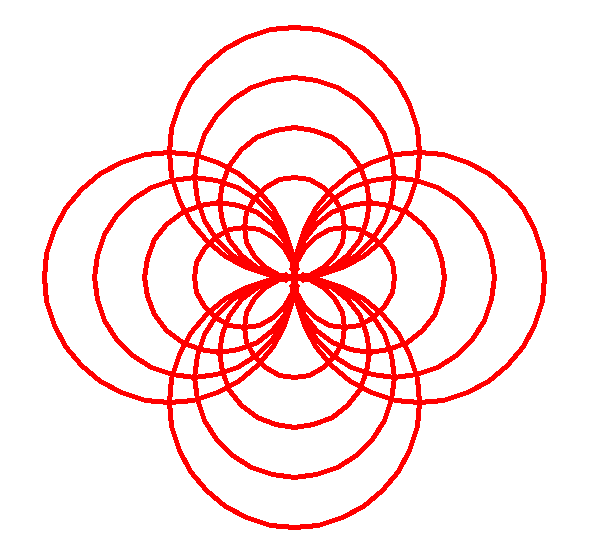
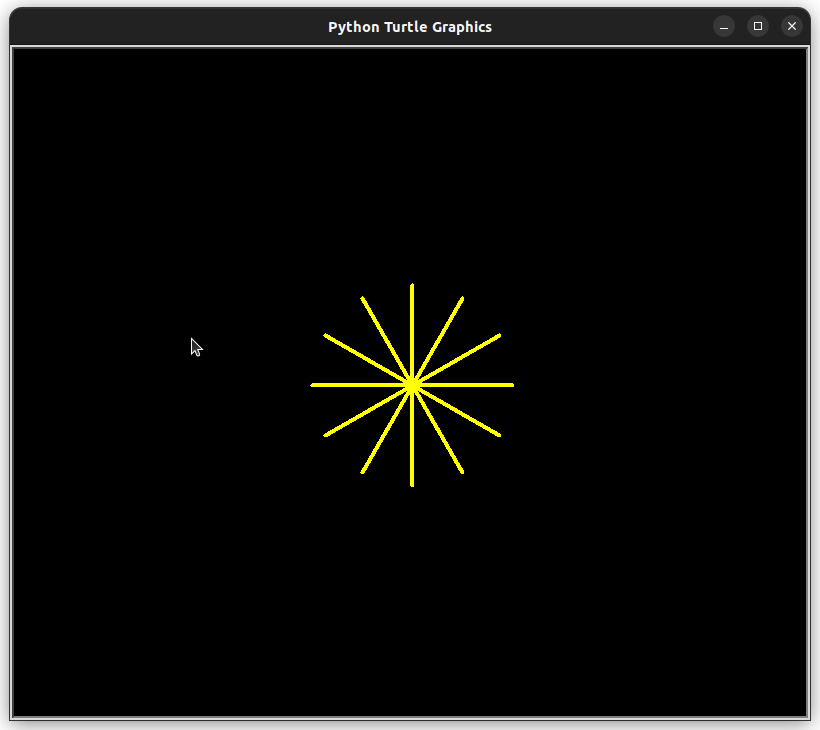
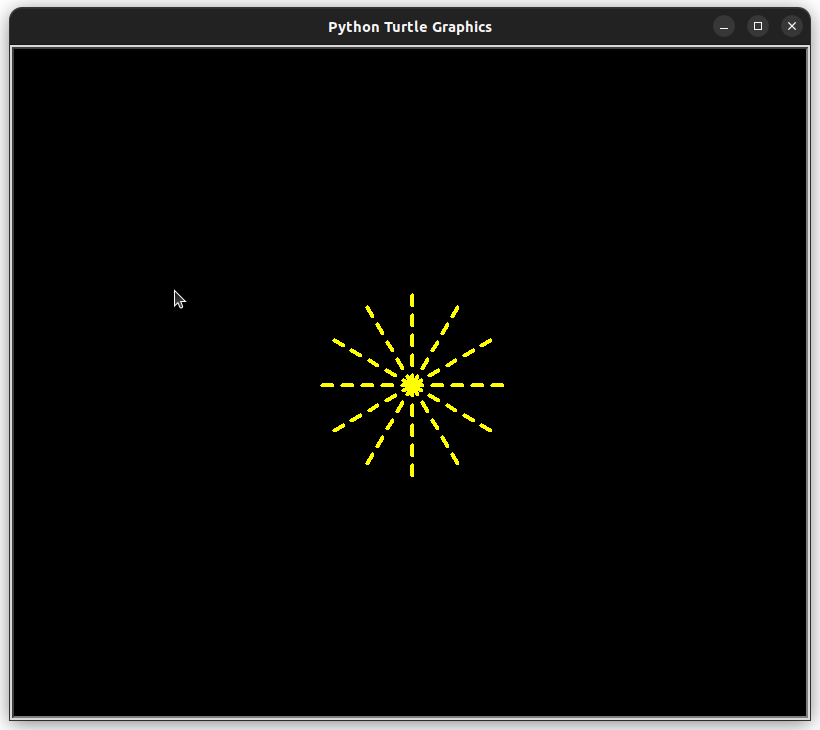
| # 1 - Importations
import turtle as trt
# 2 - CONSTANTES
FOND = "black"
COULEUR_ETOILE = "yellow"
TAILLE_ETOILE = 100
EPAISSEUR_RAYON = 4
# 3 - Déclaration de fonction
def trait(feutre, angle, distance, coord):
crayon.penup()
crayon.goto(coord[0], coord[1]) # on part au point de départ
crayon.pendown()
crayon.setheading(angle) # on s'oriente vers la droite
crayon.forward(distance) # on affiche de la bonne distance
# 3 - Programme principal
trt.bgcolor(FOND) # On définit un fond coloré noir
crayon = trt.Turtle() # On définit un crayon
crayon.color(COULEUR_ETOILE)
crayon.pensize(EPAISSEUR_RAYON)
trait(crayon, 30, TAILLE_ETOILE, (0,0)) # Rayon d'angle 0°
trait(crayon, 30, TAILLE_ETOILE, (0,0)) # Rayon d'angle 30°
trait(crayon, 60, TAILLE_ETOILE, (0,0)) # Rayon d'angle 60°
trait(crayon, 90, TAILLE_ETOILE, (0,0)) # Rayon d'angle 90°
trait(crayon, 120, TAILLE_ETOILE, (0,0)) # Rayon d'angle 120°
trait(crayon, 150, TAILLE_ETOILE, (0,0)) # Rayon d'angle 150°
trait(crayon, 180, TAILLE_ETOILE, (0,0)) # Rayon d'angle 180°
trait(crayon, 210, TAILLE_ETOILE, (0,0)) # Rayon d'angle 210°
trait(crayon, 240, TAILLE_ETOILE, (0,0)) # Rayon d'angle 240°
trait(crayon, 270, TAILLE_ETOILE, (0,0)) # Rayon d'angle 270°
trait(crayon, 300, TAILLE_ETOILE, (0,0)) # Rayon d'angle 300°
trait(crayon, 330, TAILLE_ETOILE, (0,0)) # Rayon d'angle 330°
crayon.hideturtle()
|