21 - ABR des Pokemons

⏪

⏬

⏩

1 - Collection

2 - Récupération

3 - Recherche

4 - Particularités

5 - ABR dico

6 - FAQ

Nous avons vu que la recherche dans un Arbre Binaire était plus efficace lorsqu'on sait où chercher.

On obtient alors un coût linéaire en fonction de la hauteur, qu'on peut écrire avec la complexité 𝓞(h).

Si l'AB est parfait, complet ou équilibré, on obtient une recherche à coût logarithmique sur la taille n de l'Arbre : on peut écrire 𝓞(log₂(n))
Si l'AB est filiforme, on retrouve un coût linéaire par rapport à la taille n : on peut écrire 𝓞(n)
Si l'AB est quelconque, on est entre les deux.

L'Arbre Binaire de Recherche est un AB dans lequel le placement des noeuds est lié à la valeur de la clé du noeud, ce qui facilite la recherche.

Nous allons aujourd'hui utiliser le fichier CSV de 1er sur les pokemons (et faire quelques révisions sur leurs utilisations). Mais plutôt que de placer les enregistrements dans une Collection-tableau comme en 1er, nous allons placer les enregistrements dans une Collection-ABR pour optimiser les recherches.

Image tirée du site https://boutiquepokemon.com

Logiciel nécessaire pour l'activité : -

Prérequis :

Algos : ABR

Evaluation ✎ :

Résumé : Version HTML ou fond blanc ou ou PDF (couleur ou gris)

MODE COURS (cacher les questions)

1 - Collection des pokemons

⇩ ⇧ ⤊

Rappel : Fichier CSV

Nous allons récupérer un fichier CSV contenant les données de 800 Pokémons. Pour rappel, il s'agit d'un simple fichier texte :

Un enregistrement (un Pokemon) par ligne : le passage à la ligne est donc le caractére séparateur pour les enregistrements.
Sur chaque enregistrement, les différents attributs sont séparés par une virgule (ou un point-virgule ou n'importe quel caractère précisé)

Si on rajoute les éléments importants en rouge (dont le passage à la ligne ↲ ) :

#,Name,Type 1,Type 2,Total,HP,Attack,Defense,Sp. Atk,Sp. Def,Speed,Generation,Legendary↲
1,Bulbasaur,Grass,Poison,318,45,49,49,65,65,45,1,False↲
2,Ivysaur,Grass,Poison,405,60,62,63,80,80,60,1,False↲
3,Venusaur,Grass,Poison,525,80,82,83,100,100,80,1,False↲

Le but ici n'est pas de refaire l'activité visant à récupérer ces données pour les stocker dans un tableau-collection mais juste d'utiliser les enregistrements pour construire l'ABR.

Rappel : collection et enregistrements

Nous obtiendrons rapidement une variable nommée pokemons référençant un tableau qui contiendra les enregistrements-dictionnaires des différents pokemons.

Voici le début du contenu du tableau pokemons :


pokemons = [
    {
        '#': '1',
        'Name': 'Bulbasaur',
        'Type 1': 'Grass',
        'Type 2': 'Poison',
        'Total': '318',
        'HP': '45',
        'Attack': '49',
        'Defense': '49',
        'Sp. Atk': '65',
        'Sp. Def': '65',
        'Speed': '45',
        'Generation': '1',
        'Legendary': 'False'
    },
    {'#': '2', 'Name': 'Ivysaur', 'Type 1': 'Grass', 'Type 2': 'Poison', 'Total': '405', 'HP': '60', 'Attack': '62', 'Defense': '63', 'Sp. Atk': '80', 'Sp. Def': '80', 'Speed': '60', 'Generation': '1', 'Legendary': 'False'},
    {'#': '3', 'Name': 'Venusaur', 'Type 1': 'Grass', 'Type 2': 'Poison', 'Total': '525', 'HP': '80', 'Attack': '82', 'Defense': '83', 'Sp. Atk': '100', 'Sp. Def': '100', 'Speed': '80', 'Generation': '1', 'Legendary': 'False'},
    {'#': '3', 'Name': 'VenusaurMega Venusaur', 'Type 1': 'Grass', 'Type 2': 'Poison', 'Total': '625', 'HP': '80', 'Attack': '100', 'Defense': '123', 'Sp. Atk': '122', 'Sp. Def': '120', 'Speed': '80', 'Generation': '1', 'Legendary': 'False'},
    ...
]

01° Comment obtenir l'enregistrement d'indice 0 contenu dans pokemons ? Quel est le type de cet enregistrement ?

Correction ?

...CORRECTION...


>>> pokemons[0]
 {'#': '1', 'Name': 'Bulbasaur', 'Type 1': 'Grass', 'Type 2': 'Poison', 'Total': '318', 'HP': '45', 'Attack': '49', 'Defense': '49', 'Sp. Atk': '65', 'Sp. Def': '65', 'Speed': '45', 'Generation': '1', 'Legendary': 'False'}

On obtient un enregistrement sous forme de dictionnaire.

02° Quelle est la méthode permettant d'obtenir l'ensemble des clés disponibles sur ce dictionnaire-enregistrement ?

Comment afficher les clés une par une avec un simple print() ?

Correction ?

...CORRECTION...


>>> pokemons[0].keys()
dict_keys(['#', 'Name', 'Type 1', 'Type 2', 'Total', 'HP', 'Attack', 'Defense', 'Sp. Atk', 'Sp. Def', 'Speed', 'Generation', 'Legendary'])
 
>>> for c in pokemons[0].keys(): print(c)
 #
 Name
 Type 1
 Type 2
 Total
 HP
 Attack
 Defense
 Sp. Atk
 Sp. Def
 Speed
 Generation
 Legendary

03° Comment afficher les couples (clé, valeur) (un par un) sur cet enregistrement-dictionnaire ?

Correction ?

...CORRECTION...


>>> for couple in pokemons[0].items(): print(couple)
 ('#', '1')
 ('Name', 'Bulbasaur')
 ('Type 1', 'Grass')
 ('Type 2', 'Poison')
 ('Total', '318')
 ('HP', '45')
 ('Attack', '49')
 ('Defense', '49')
 ('Sp. Atk', '65')
 ('Sp. Def', '65')
 ('Speed', '45')
 ('Generation', '1')
 ('Legendary', 'False')

04° Comment afficher les couples (c, v) (un par un) sous la forme "La clé {c} est associée à la valeur {v}" ?

Correction ?

...CORRECTION...


>>> for (c,v) in pokemons[0].items(): print(f"La clé {c} est associée à la valeur {v}")
 La clé # est associée à la valeur 1
 La clé Name est associée à la valeur Bulbasaur
 La clé Type 1 est associée à la valeur Grass
 La clé Type 2 est associée à la valeur Poison
 La clé Total est associée à la valeur 318
 La clé HP est associée à la valeur 45
 La clé Attack est associée à la valeur 49
 La clé Defense est associée à la valeur 49
 La clé Sp. Atk est associée à la valeur 65
 La clé Sp. Def est associée à la valeur 65
 La clé Speed est associée à la valeur 45
 La clé Generation est associée à la valeur 1
 La clé Legendary est associée à la valeur False

05° Comment obtenir la valeur associée à la clé "Attack" pour l'enregistrement d'indice 0 contenu dans pokemons ?

Correction ?

...CORRECTION...


>>> pokemons[0]["Attack"]
'49'

06° Comment faire la même chose mais en récupérant un entier ?

Correction ?

...CORRECTION...


>>> int(pokemons[0]["Attack"])
49

2 - Récupération des données

⇩ ⇧ ⤊

Nous allons maintenant télécharger directement le fichier CSV et différents modules :

Un module creation_collect permettant de créer la collection sous forme d'un tableau de dictionnaire
Un module abr permettant de gérer les ABR

La différence fondamentale entre ce module abr et notre ancien module abr est que désormais, le contenu d'un noeud doit être un couple contenant

En indice 0, la clé de ce noeud;
En indice 1, les données associées à ce noeud : nous y placerons le dictionnaire-enregistrement-pokemon.

07° Créer puis lancer ce programme Python en le nommant telechargement.py et en le plaçant dans un nouveau dossier nommé tp_pok.

📁 tp_pok

📄 telechargement.py

import urllib.request
 
urllib.request.urlretrieve('https://gist.githubusercontent.com/armgilles/194bcff35001e7eb53a2a8b441e8b2c6/raw/92200bc0a673d5ce2110aaad4544ed6c4010f687/pokemon.csv', 'mesdonnees.csv')
urllib.request.urlretrieve('https://doc.infoforall.fr/activite/algo/scripts/arbre_a_pokemons/creation_collect.py', 'creation_collect.py')
urllib.request.urlretrieve('https://doc.infoforall.fr/activite/algo/scripts/arbre_a_pokemons/tp_arbre_pokemons.py', 'tp_arbre_pokemons.py')
urllib.request.urlretrieve('https://doc.infoforall.fr/activite/algo/scripts/arbre_a_pokemons/abr.py', 'abr.py')

En cas de problème (le réseau peut vous empêcher d'utiliser correctement le module request), téléchargez simplement ces fichiers à la main en utilisant les liens ci-dessous.

Vous allez alors normalement obtenir plusieurs nouveaux fichiers dans votre dossier :

📁 tp_pok

📄 telechargement.py

📄 abr.py

📄 creation_collect.py

📄 tp_arbre_pokemons.py

📄 mes_donnees.csv

08° Ouvrir dans Thonny le fichier nommé tp_arbre_pokemons.py.

Importer dans Thonny le module nommé binarytree qui va être nécessaire au fonctionnement de notre propre module (Outils, puis Gérer les paquets).

Mettre le programme en mémoire puis lancer les commandes suivantes pour vérifier que la documentation est bien présente :


>>> help(nv_AB)
 
>>> help(inserer_noeud_dans_ABR)

Est-il clairment indiqué qu'on doit envoyé un tuple en tant qu'élément lorsqu'on veut créer un nouvel arbre ?
Peut-on voir que certains paramètres ont une valeur par défaut ?
Peut-on voir qu'en réalité les objets ABR, Noeud... sont issus du module abr.py ?

Correction ?

...CORRECTION...

Lorsqu'on demande à visualiser quelques explications d'aide, on obtient ceci :


>>> help(nv_AB)
Help on function nv_AB in module abr:
 
nv_AB(valeur: 'tuple(cle,data)', g: 'AB|None' = None, d: 'AB|None' = None) -> 'AB NON VIDE'
    Renvoie un nouvel Arbre Binaire dont la racine porte valeur et qui mène aux sous-arbres g et d

 
>>> help(inserer_noeud_dans_ABR)
Help on function inserer_noeud_dans_ABR in module abr:
 
inserer_noeud_dans_ABR(arbre: 'ABR NON VIDE', nd: 'Noeud') -> None
    Insére le noeud au bon endroit dans l'ABR NON VIDE

La documentation indique clairement qu'on doit envoyé en tant que valeur un couple comportant d'abord la clé puis les données associées.
On voit dans le prototype de nv_AB qui les paramètres ont des valeurs par défaut.
On trouve au début de chacune des lignes une indication comme Help on function *** in module abr qui montre clairement qu'on parle d'une fonction inclue dans le module abr.

09° Dessiner sur papier l'arbre créé en utilisant la fonction de test creation_test() suivante du script tp_arbre_pokemons.py :

Visualisez bien qu'on envoie deux tuples désormais à la fonction qui crée un nouvel arbre : on stocke la clé et les données associées à notre noeud. Ici, on ne stocke aucune donnée en plus de la clé : on envoie donc None en tant que données.

def creation_test() -> 'ABR' :
    """Renvoie un ABR de test"""
     
    arbre = nv_AB((20, None))
    inserer_noeud_dans_ABR(arbre, nv_AB((25, None)))    
    inserer_noeud_dans_ABR(arbre, nv_AB((15, None)))    
    inserer_noeud_dans_ABR(arbre, nv_AB((17, None)))    
    inserer_noeud_dans_ABR(arbre, nv_AB((10, None)))
    return arbre

Vérifier ensuite votre réponse en tapant simplement ceci :


>>> arbre = creation_test()
>>> print(arbre)

Correction ?

...CORRECTION...


>>> arbre = creation_test()
>>> print(arbre)

     ____20
    /      \
  _15       25
 /   \
10    17

10° Rajoutons un noeud dont la clé est 21.

Vérifier qu'il se positionne bien en affichant l'arbre.


>>> inserer_noeud_dans_ABR(arbre, nv_AB((21, None)))

Correction ?

...CORRECTION...


>>> inserer_noeud_dans_ABR(arbre, nv_AB((21, None)))
>>> print(arbre)

     ____20___
    /         \
  _15         _25
 /   \       /
10    17    21

Voyons maintenant comment récupérer les données de nos Pokemons avec le module.

11° Nous allons utiliser la fonction creation_collection_pokemons() présente dans tp_arbre_pokemons.py : elle ouvre le fichier CSV et place les données lues dans une Collection de dictionnaires dont elle renvoie la référence.

22
23
24

def creation_collection_pokemons() -> list[dict] :
    """Renvoie une collection-tableau de dictionnaires des pokemons"""
    return creer_collection('mesdonnees.csv')

En regardant les importations présentes au début du fichier tp_arbre_pokemons.py, donner des explications liées à ces questions ::

dans quel module se trouve en réalité la fonction creer_collection()
pourquoi on a le droit de l'utiliser en notant simplement creer_collection mais pas nom_du_module.creer_collection

Correction ?

...CORRECTION...

La partie importation est celle-ci :

 1
 2

# Importations
from creation_collect import creer_collection

On voit donc que la fonction est dans le module creation_collect

On peut l'utiliser directement en notant creer_collection car creer_collection est directement derrière import.

12° Utiliser le jeu de commandes suivants pour comprendre ce que contient le tableau-collection collect :


>>> collect = creation_collection_pokemons()
>>> len(collect)
800
 
>>> collect[0]
{'#': '1', 'Name': 'Bulbasaur', 'Type 1': 'Grass', 'Type 2': 'Poison', 'Total': '318', 'HP': '45', 'Attack': '49', 'Defense': '49', 'Sp. Atk': '65', 'Sp. Def': '65', 'Speed': '45', 'Generation': '1', 'Legendary': 'False'}
 
>>> collect[1]
{'#': '2', 'Name': 'Ivysaur', 'Type 1': 'Grass', 'Type 2': 'Poison', 'Total': '405', 'HP': '60', 'Attack': '62', 'Defense': '63', 'Sp. Atk': '80', 'Sp. Def': '80', 'Speed': '60', 'Generation': '1', 'Legendary': 'False'}
 
>>> for i in range(0, 10, 1): print(collect[i]['Name'])
 
 Bulbasaur
 Ivysaur
 Venusaur
 VenusaurMega Venusaur
 Charmander
 Charmeleon
 Charizard
 CharizardMega Charizard X
 CharizardMega Charizard Y
 Squirtle

Correction ?

...CORRECTION...

Nous retrouvons ce que nous avons vu en partie 1.

collect est un tableau qui contient des dictionnaires.

Chaque dictionnaire possède les mêmes clés : on dit que ce sont des enregistrements.

On accède à l'un des attributs d'un enregistrement en donnant simplement le nom de la clé correspondante.

Essayons maintenant de voir ce que fait la fonction creation_arbre_pokemons() du fichier tp_arbre_pokemons.py.

13° Observer les instructions de la fonction creation_arbre_pokemons() et répondre aux questions :

def creation_collection_pokemons() -> list[dict]:
    """Renvoie une collection-tableau de dictionnaires des pokemons"""
    return creer_collection('mesdonnees.csv')
 
def creation_arbre_pokemons(type_cle=int, attribut='Attack') -> 'ABR' :
    """Renvoie un ABR de pokemons en utilisant le type et l'attribut fourni comme clé d'ABR"""
 
    pokemons = creer_collection('mesdonnees.csv') 
    arbre = nv_ABV()
 
    for i in range(len(pokemons)):
        d = pokemons[i]            # d pour data (pour ne pas confondre avec la fonction data)
        c = type_cle(d[attribut])  # c pour cle (pour ne pas confondre avec la fonction cle)
        contenu = (c, d)
        noeud_unique = nv_AB(contenu)
 
        if est_ABV(arbre):
            arbre = noeud_unique
        elif i < 41:
            inserer_noeud_dans_ABR(arbre, noeud_unique)
 
    return arbre

Ligne 26 : quel est l'attribut du dictionnaire choisi pour jouer le rôle de clé par défaut dans l'arbre ? Quel est le type par défaut de cette clé ?
Ligne 30 : quel est le contenu de l'arbre initialement ?
Ligne 32 : la base des pokemons contient 800 pokemons. Quel va être la valeur finale de la variable de boucle i ?
Ligne 33 : à chaque tour de boucle, quel est le type de la variable d ?
Ligne 34 : à chaque tour de boucle, la variable c va t-elle contenir un string ou un entier ?
Ligne 35 : Quel est le type de la variable contenu ?
Ligne 38 et +

Que fait-on si l'arbre est vide lors du premier tour de boucle ?
Que fait-on si l'arbre n'est pas vide lors des autres tours de boucle ?
Quelle va être la taille de l'arbre à la fin de la boucle POUR ?

Correction ?

...CORRECTION...

Ligne 26 : on utilise par défaut la valeur Attack sous forme d'un integer.
Ligne 30 : vide puisqu'on crée un AB VIDE.
Ligne 32 : 800 donc de 0 à 799.
Ligne 33 : pokemons est de type list[dict]. La variable d référence pokemons[i], il s'agit donc d'un dictionnaire.
Ligne 34 : on va chercher la valeur associée à la clé "Attack" dans le dictionnaire et on tente de le transformer en entier. Il s'agit donc de l'attaque de ce pokemon sous forme d'un entier.
Ligne 35 : Il s'agit du tuple, le couple (cle du noeud, contenu associé à ce noeud).
Ligne 38 et +

Si l'arbre est vide, on utilise l'arbre ne contenant qu'un seul noeud comme arbre de départ. La racine de notre arbre sera donc nécessairement liée au premier pokemon de la collection : Bulbasaur.
Si l'arbre n'est pas vide et que l'indice de l'enregistrement est compris entre 0 et 40, on rajoute le nouveau pokemon à l'ABR en utilisant son attaque comme clé.
Au total : on aura des noeuds correspondants aux pokemons n°0 à n°40. La taille de l'arbre est donc 41 puisqu'on aura 41 pokemons stockés.

14° Utilisez le code suivant pour voir le principe de nos enregistrements stockés dans l'arbre à Pokemons (apok):


>>> apok = creation_arbre_pokemons()
>>> print(apok)

Pour réduire la taille de la police de la console de Thonny, il suffit de placer la souris dans la console et d'appuyer sur CTRL et -.

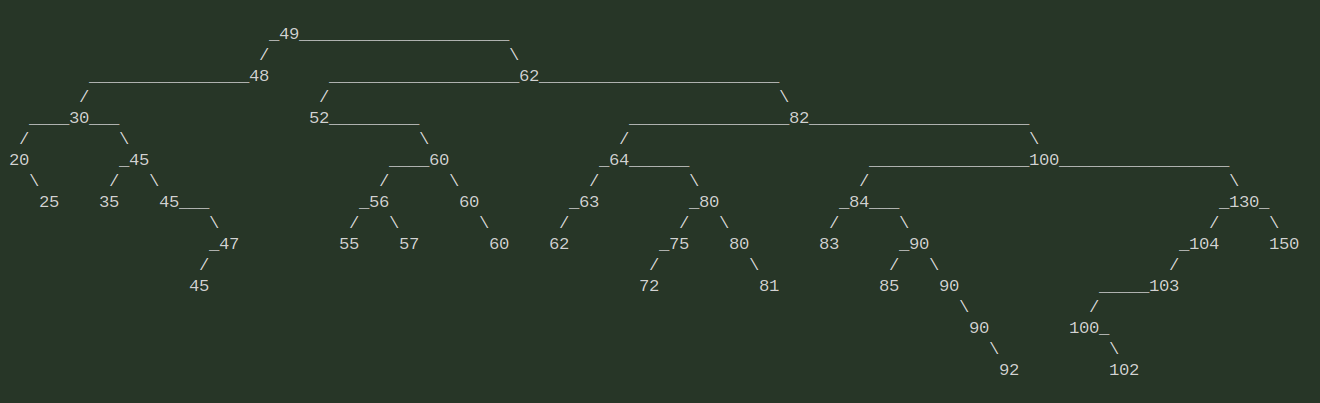
Question : la création directe et brute de l'arbre à partir des Pokemons lus dans le fichier CSV donne-t-il un arbre équilibré AVL (la différence de profondeur entre les sous-arbres gauche et droite est de un au maximum) ?

Correction ?

...CORRECTION...

On rajoute les noeuds un peu au hasard. On peut donc avoir un arbre équilibré ou pas. Ici, on obtient un arbre qui n'est ni parfait, ni complet, ni équilibré AVL.

15° Utilisez les instructions suivantes pour voir comment naviguer manuellement dans l'arbre et récupérer certaines données :


>>> cle(racine(apok))
49
 
>>> data(racine(apok))
{'#': '1', 'Name': 'Bulbasaur', 'Type 1': 'Grass', 'Type 2': 'Poison', 'Total': '318', 'HP': '45', 'Attack': '49', 'Defense': '49', 'Sp. Atk': '65', 'Sp. Def': '65', 'Speed': '45', 'Generation': '1', 'Legendary': 'False'}
 
>>> data(racine(apok))['Name']
'Bulbasaur'
 
>>> g = gauche(apok)
>>> data(racine(g))['Name']
'Squirtle'
 
>>> cle(racine(g))
48
 
>>> d = droite(apok)
>>> data(racine(d))['Name']
'Ivysaur'
 
>>> cle(racine(d))
62

16° Si on suppose que l'ABR est équilibré, quel est le coût d'une insertion ?

Correction ?

...CORRECTION...

L'insertion d'un Noeud possède un coût linéaire par rapport à la hauteur : 𝓞(h).

Pour un arbre (parfait, ou complet, ou équilibré), on obtient alors un coût logarithmique sur la taille n de l'Arbre : on peut écrire 𝓞(log₂(n))

3 - Recherche

⇩ ⇧ ⤊

17° Ouvrir le fichier abr.py du module abr.

Implémenter l'algorithme de recherche dans un arbre binaire de recherche en utilisant les fonctions d'interface disponibles. Voici le prototype visé :

recherche(arbre:ABR, cr:Cle) -> ABR|ABV

Notre fonction devra donc renvoyer la référence d'un Noeud comportant cette clé, ou ne rien renvoyer si aucun noeud ne correspond.

1
2
3

def recherche(arbre:'ABR', cr: 'clé') -> 'ABR':
    """Recherche un noeud portant la bonne clé et renvoie sa référence"""
    return nb_ABV()

Une fois implémentée, tester la fonction puis fournir l'autre implémentation possible. Vous devriez au final avoir une implémentation avec un TANT QUE et une implémentation récursive.

Correction ?

...CORRECTION...

Version avec TANT QUE :

def recherche(arbre:'ABR', cr: 'clé') -> 'ABR':
    """Recherche un noeud portant la bonne clé et renvoie sa référence"""
     
    reponse = nv_ABV()
     
    while not est_ABV(arbre):
        if cr == cle(racine(arbre)):
            reponse = arbre
            arbre = nv_ABV()
        elif cr < cle(racine(arbre)):
            arbre = gauche(arbre)
        elif cr > cle(racine(arbre)):
            arbre = droite(arbre)
 
    return reponse

Version RECURSIVE :

def recherche(arbre:'ABR', cr: 'clé') -> 'ABR':
    """Recherche un noeud portant la bonne clé et renvoie sa référence"""
     
    if est_ABV(arbre):
        return arbre
    elif cr == cle(racine(arbre)):
        return arbre
     
    elif cr < cle(racine(arbre)):
        return recherche(gauche(arbre), cr)
    elif cr > cle(racine(arbre)):
        return recherche(droite(arbre), cr)

18° Tester l'absence d'erreur en lançant directement le module abr.py.

Vérifiez ensuite que la fonction fonctionne : relancer le programme tp_arbre_pokemons.py puis lancer ces commandes :


>>> apok = creation_arbre_pokemons()
>>> print(apok)
>>> recherche(apok, 49)
<abr.AB object at 0x7f0da76a0e48>
 
>>> arbre_reponse = recherche(apok, 102)
>>> data(arbre_reponse)['Name']
'Nidoking'

19° Si on suppose que l'ABR est au moins équilibré, quel est le coût d'une recherche ?

Correction ?

...CORRECTION...

La recherche d'un Noeud possède un coût linéaire par rapport à la hauteur : 𝓞(h).

Pour un arbre parfait, complet ou équilibré, on obtient alors un coût logarithmique sur la taille n de l'Arbre : on peut écrire 𝓞(log₂(n))

4 - Affichage particulier

⇩ ⇧ ⤊

3 avantages de l'ABR : affichage trié, max et min

Affichage trié :: les noeuds sont déjà 'triés' entre eux. On peut les afficher un par un de façon triée via un parcours en profondeur d'abord infixe (la racine au milieu de l'affichage) !
Recherche facile du minimum : pour trouver la plus petite clé disponible, il suffit d'aller le plus à gauche possible (tant que le sous-arbre de destination n'est pas vide).
Recherche facile du maximum : pour trouver la plus grande clé, il suffit d'aller le plus à droite possible (tant que le sous-arbre de destination n'est pas vide).

20° Afficher les attaques des 41 Pokemons stockées pour l'instant en utilisant simplement la fonction parcours_infixe() :


>>> parcours_infixe(apok)
20
25
30
35
45
45
45
47
48
49
52
55
56
57
60
60
60
62
62
63
64
72
75
80
80
81
82
83
84
85
90
90
90
92
100
100
102
103
104
130
150

21° Modifier parcours_infixe() : il faudra afficher également le nom du Pokemon à côté de son score d'attaque.


>>> apok = creation_arbre_pokemons()
>>> parcours_infixe(a)
 20 pour Metapod
 25 pour Kakuna
 30 pour Caterpie
 35 pour Weedle
 45 pour Butterfree
 45 pour Pidgey
 45 pour Clefairy
 47 pour Nidoran♀
 48 pour Squirtle
 49 pour Bulbasaur
 52 pour Charmander
 55 pour Pikachu
 56 pour Rattata
 57 pour Nidoran♂
 60 pour Pidgeotto
 60 pour Spearow
 60 pour Ekans
 62 pour Ivysaur
 62 pour Nidorina
 63 pour Wartortle
 64 pour Charmeleon
 72 pour Nidorino
 75 pour Sandshrew
 80 pour Pidgeot
 80 pour PidgeotMega Pidgeot
 81 pour Raticate
 82 pour Venusaur
 83 pour Blastoise
 84 pour Charizard
 85 pour Arbok
 90 pour Beedrill
 90 pour Fearow
 90 pour Raichu
 92 pour Nidoqueen
 100 pour VenusaurMega Venusaur
 100 pour Sandslash
 102 pour Nidoking
 103 pour BlastoiseMega Blastoise
 104 pour CharizardMega Charizard Y
 130 pour CharizardMega Charizard X
 150 pour BeedrillMega Beedrill

Correction ?

...CORRECTION...

def parcours_infixe(arbre):
    """Exploration (et affichage) en profondeur en infixe GRD"""
    if not estArbreVide(arbre):
        parcours_infixe(gauche(arbre))
        print(f"{cle(racine(arbre))} pour {data(racine(arbre))['Name']}")
        parcours_infixe(droite(arbre))

22° A droite toute : rajouter dans le programme TP la fonction récursive cle_max() : on transfère la plus grande valeur. Il suffit donc d'aller à droite tant qu'on le peut.

def cle_max(arbre:'ABR NON VIDE', maximum=None) -> 'type des clés de cet ABR':
    if est_ABV(arbre):
        return maximum
    else:
        maximum = cle(racine(arbre))
        return cle_max(droite(arbre), maximum)

Lors du premier appel, maximum n'est pas fourni et prend donc la valeur None. Ensuite, on cherche la valeur de la clé de la racine actuelle, et on part à droite pour recommencer. Le cas de base : on tombe sur un arbre vide. Cela veut dire qu'on peut cesser d'appeler quelqu'un d'autre : il suffit de renvoyer le maximum détecté.

Utilisation :


>>> apok = creation_arbre_pokemons()
>>> cle_max(apok)
150
 
>>> data(recherche(apok, 150))['Name']
'BeedrillMega Beedrill'

23° A gauche toute : créer dans le programme TP la fonction récursive cle_min() : on transfère la plus petite valeur à chaque appel :!

Correction ?

...CORRECTION...

def cle_min(arbre:'ABR NON VIDE', minimum=None) -> 'type des clés de cet ABR':
    if est_ABV(arbre):
        return minimum
    else:
        minimum = cle(racine(arbre))
        return cle_max(gauche(arbre), minimum)

24° Libérez les 800 Pokemons : dans creation_arbre_pokemons(), remplacez elif i < 41: par un simple else: sans condition. Cela vous permettra d'aller au bout de la collection. Attention, dans cette version, si vous voulez profiter de l'affichage avec print, la clé devra être un entier.

5 - ABR sous forme d'un ensemble de dictionnaires

⇩ ⇧ ⤊

Plutôt que d'utiliser la POO, nous pourrions utiliser le type construit dict pour implémenter les arbres.

Ainsi, un ABR VIDE peut être le dictionnaire
{'v':None, 'g':None, 'd':None}

De même, un ABR composé uniquement d'un noeud peut être le dictionnaire
{'v':(5, None), 'g':{'v':None, 'g':None, 'd':None}, 'd':{'v':None, 'g':None, 'd':None}}

25 - mini projet° Réaliser une nouvelle version du fichier abr.py : on n'y implémente plus les AB via des objets mais intégralement sous forme d'un dictionnaire.

6 - FAQ

⇩ ⇧ ⤊

Rien pour le moment

Activité publiée le 07 01 2021
Dernière modification : 30 01 2021
Auteur : ows. h.

⏪

⏫

⏩