22 - Diviser pour régner
L'an dernier, nous avons vu deux moyens de résoudre un problème compliqué :
Moyen n°1 : le premier moyen est la force brute.
- Principe : on y va franchement, on calcule tout, quitte à calculer les choses plusieurs fois, voire à calculer des choses qui ne servent en rien pour trouver la solution.
- Type de problème : tous les problèmes à priori.
Moyen n°2 : le deuxième moyen est de passer par la stratégie gloutonne.
- Principe : on ne regarde pas le problème dans sa totalité. On prend une décision purement locale, de façon définitive et sans se soucier de ce que va devenir le problème restant à traiter. On obtient alors un problème un peu plus petit. On prend une deuxième décision purement locale, qui va encore réduire la taille du problème restant à traiter. Et on continue, en prenant une autre décision locale jusqu'à obtenir une solution à notre grand problème initial.
- Type de problème : ceux pour lesquels on peut trouver plusieurs solutions, optimales ou pas.
Un exemple avec Mr Glouton dont l'objectif est d'aller vers la case en bas à droite en mangeant mal (il préfère la malbouffe salée, sinon la sucrée ça va aussi, et s'il doit vraiment manger des carottes ou de la salade, pourquoi pas...).
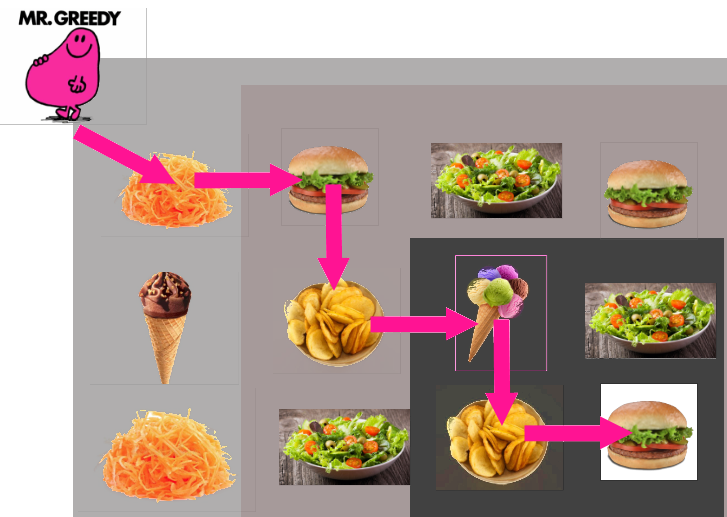
Comme on le voit, la taille du problème à traiter diminue à chaque décision.
Moyen n°3 : aujourd'hui, nous allons voir la stratégie diviser pour régner.
Evaluation ✎ :
Documents de cours : open document ou pdf
1 - Principe du diviser pour régner
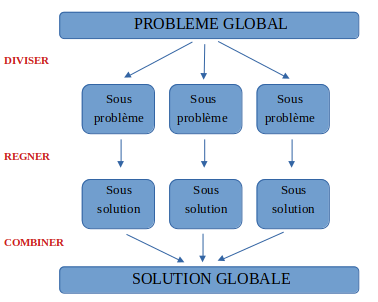
Le principe de cette stratégie est de résoudre le problème selon cette structure :
Diviser pour régner
- Phase DIVISER : on divise le problème global jusqu'à obtenir un ensemble de petits problèmes faciles à résoudre.
- Phase REGNER : on règne sur le sous-problème plus petit et qui est donc gérable.
- Phase COMBINER : on combine les différentes sous-solutions pour obtenir la solution au problème global.
Différence avec la stratégie gloutonne ?
Deux différences principales :
- Le sens de déroulement
- La stratégie gloutonne réduit définitivement la taille du problème à chaque étape. C'est une méthode HAUT - BAS sans remonter ensuite vers le haut, pas de phase COMBINER.
- La stratégie diviser pour régner réduit la taille du problème puis combine les sous-solutions. C'est une méthode HAUT-BAS-HAUT à cause de la phase COMBINER.
- Le type du problème qu'on tente de résoudre
- La stratégie gloutonne vise à résoudre des problèmes particuliers : ceux pour lesquels il existe beaucoup de solutions dont la qualité est variable : certaines sont optimales, d'autres acceptables et les dernières de "mauvaise qualité". Le problème du voyageur de commerce peut être résolu avec une stratégie gloutonne puisqu'on peut trouver plusieurs chemins entre les différentes villes.
- La stratégie diviser pour régner vise à résoudre des problèmes pour lequel il n'existe qu'une solution. Le problème de la présence d'un élément dans un tableau peut être résolu par une stratégie diviser pour régner puisqu'il n'existe qu'une bonne réponse possible : là ou pas là.
01° Pourquoi la recherche dichotomique fait partie des stratégies diviser pour régner plutôt que des stratégies gloutonnes alors qu'on fait bien un choix local à chaque étape ?
On rappelle ci-dessous le principe de la recherche dichotomique dans un tableau trié si vous avez oublié.
...CORRECTION...
On réduit bien définitivement la taille du problème à chaque étape (on dit oui ou on supprime la partie gauche ou droite) et il n'y a pas vraiment de phase COMBINER. Cela ressemble à du glouton.
Pourquoi est-ce du diviser pour régner ? Simplement car il n'y a qu'une réponse possible et pas plusieurs réponses plus ou moins pertinente.
La recherche par dichotomie est donc bien un algorithme basé sur la stratégie diviser pour régner. C'est même un cas très simple car la phase COMBINER ne combine rien : on peut répondre sans avoir à recombiner les différences réponses.
Algorithme de recherche dichotomique
But : trouver si un élément recherché existe bien dans un tableau. S'il existe, on fournit l'indice de la première occurrence trouvée. Sinon, il renvoie une réponse vide.
Principe : dans un tableau trié, on regarde la valeur centrale dans les indices encore disponibles. S'il ne s'agit pas de la bonne valeur, on enlève de l'intervalle de recherche les indices qui ne peuvent pas contenir la valeur recherchée.
Description des entrées / sortie
ENTREES:tableau: un tableau trié contenant un ensemble d'éléments.x: un élément voulu qu'on tente de rechercher dans le tableau- (optionnelle selon les langages d'implémentation):
longueur, le nombre d'éléments dans le tableau SORTIE: une réponse vide (à définir) ou un nombre correspondant à l'index trouvé.
Algorithme commenté
Dans l'algorithme ci-dessous, l'opérateur // désigne une division entière.
g ← 0
d ← longueur - 1
TANT QUE g <= d
m ← (g + d) // 2
SI tableau[m] < x
on ne garde que ce qui est à droite de l'indice m central
g ← (m + 1)
SINON SI tableau[m] > x
on ne garde que ce qui est à gauche de l'indice m
d ← (m - 1)
SINON
Si on arrive ici, c'est que x est bien à l'indice m
Renvoyer m
Fin du Si
Fin Tant que
Si on arrive ici, c'est que l'intervalle de recherche est vide
Renvoyer VIDE
Un exemple de cette stratégie appliquée à la rotation d'une image : on considère qu'on ne sait pas faire de rotation mais uniquement des translations.
- Phase (récursive) DIVISER : on divise l'image en 4 parties jusqu'à obtenir un pixel unique.
- Phase (récursive) REGNER : on sait faire tourner un pixel : il suffit de ne rien faire !
- Phase (récursive) COMBINER : on déplace dans le sens horaire les 4 sous-images et on les combine pour obtenir une nouvelle image plus grande.
Le plus rigolo, c'est qu'on peut placer la translation horaire des 4 sous-images pendant la phase DIVISER. C'est un cas particulier et on perd un peu le principe de ne combiner que pendant la phase COMBINER mais on retrouve un peu le positionnement de l'exploration de la racine lors des trois parcours en profondeur.
- Phase (récursive) DIVISER : on divise l'image en 4 parties et on déplace les 4 parties dans le sens horaire. On effectue cela jusqu'à obtenir un pixel unique.
- Phase (récursive) REGNER : on sait faire tourner un pixel : il suffit de ne rien faire !
- Phase (récursive) COMBINER : on combine 4 sous-images pour obtenir une nouvelle image plus grande.
Diviser pour régner pour faire tourner une image revient donc à se dire qu'on ne sait faire tourner qu'un pixel unique. On parvient donc à régner en divisant l'image en pixels.
Pas de problème pour faire tourner ce pixel bleu de 90° !
Si on doit résumer cela sur un schéma de principe :
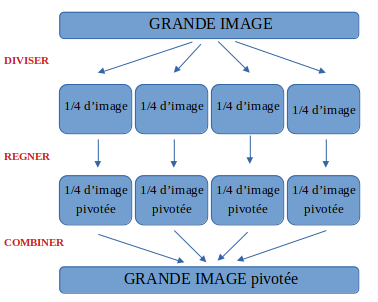
Un dernier exemple sur une image réelle on veut faire pivoter Tux, la mascotte de Linux. J'ai utilisé la méthode où la permutation des 4 sous-images en faite dès la phase DIVISER :
On peut
- calculer les nouvelles positions des pixels en faisant un peu de mathématiques, ou
- utiliser la méthode diviser pour régner. Regardez le résultat ci-dessous.
On divise Tux en quatre zones et on les décale simplement dans le sens horaire :
On divise à nouveau chacune des 4 zones en 16 sous-zones. Et dans chaque zone, on décale les sous-zones dans le sens horaire :
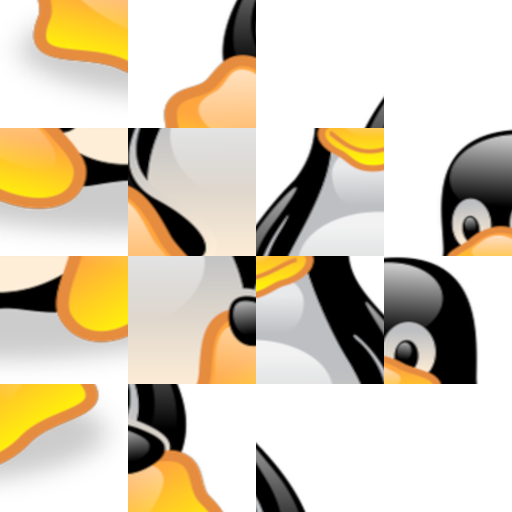
On divise à nouveau chacune des 16 sous-zones en 4, soit 64 sous-sous-zones. Et dans chaque sous-zone, on décale les sous-sous-zones dans le sens horaire :
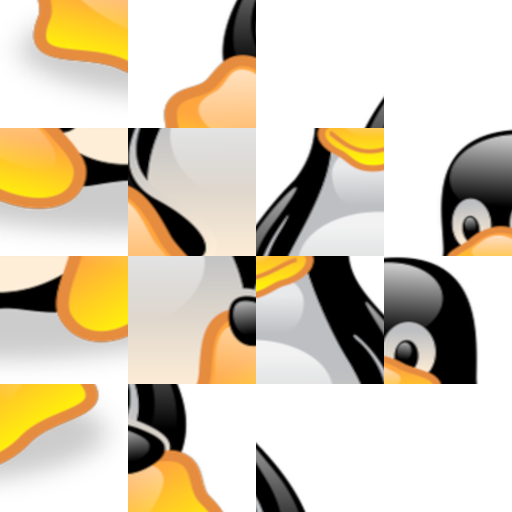
Et on continue :
Et on continue :
Et on continue :
Et encore et encore jusqu'à arriver à des sous-zones qui sont constitués uniquement de ... 1 pixel. Du coup, pas plus besoin de faire de rotation. On continue donc :
Animation finale :
On notera que c'est un exemple très visuel et donc assez pratique pour comprendre la méthode, mais que ce n'est pas efficace en terme de coût ici. On déplace et stocke chaque pixel plusieurs fois avant de lui trouver sa place définitive.
- Le coût en temps n'est pas bon
- Le coût en espace mémoire n'est pas bon non plus.
Il s'agit donc bien d'un exemple pédagogique. Il n'est pas rentable de faire tourner les images comme cela. Dans la réalité, on gère juste cela avec un peu de maths.
2 - Tri fusion, un tri en diviser pour régner
Nous avions vu l'an dernier :
- Le tri par sélection
- un tri à coût quadratique, dont la complexité est 𝞗(n2)
- principe on cherche les minimum successifs et à l'inverse avec la case 0. On continue avec minimum dans le tableau restant et on le place sur l'indice 1... Jusqu'à obtenir un tableau entièrement trié. On peut faire pareil en prenant le maximum et en le plaçant en fin de tableau.
- Le tri par insertion
- un tri à coût quadratique, dont la complexité est 𝓞(n2)
- principe : on crée un tableau d'un seul élément, puis on ramène et place correctement un deuxième élément. On continue jusqu'à ramener tous les éléments, un par un.
Introduction - Principe du tri fusion
Nous allons donc voir le tri fusion qui consiste à
- Phase DIVISER : on divise en deux notre tableau, récursivement.
- Phase REGNER : on règne sur le problème du tri lorsqu'on obtient... un tableau de une case. Il est trié !
- Phase COMBINER : on fusionne alors facilement nos deux tableaux triés : le plus petit élément de chaque tableau est au début du tableau. Trier les éléments des deux tableaux revient à lire deux valeurs à chaque étape, et faire leur comparaison.
Si n et m sont les longueurs des deux listes triées, on peut donc dire que l'étape COMBINER est à coût linéaire (en 𝞗(n+m)).
Si on résume ceci sous forme de schéma de principe :
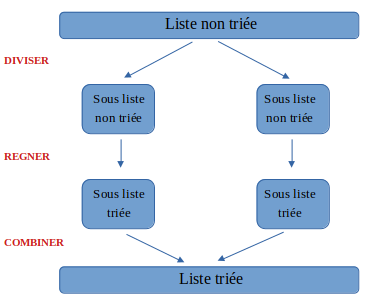
Passons à un exemple concret :
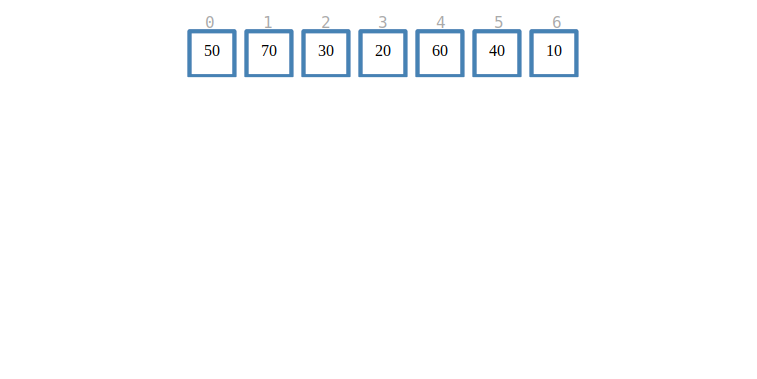
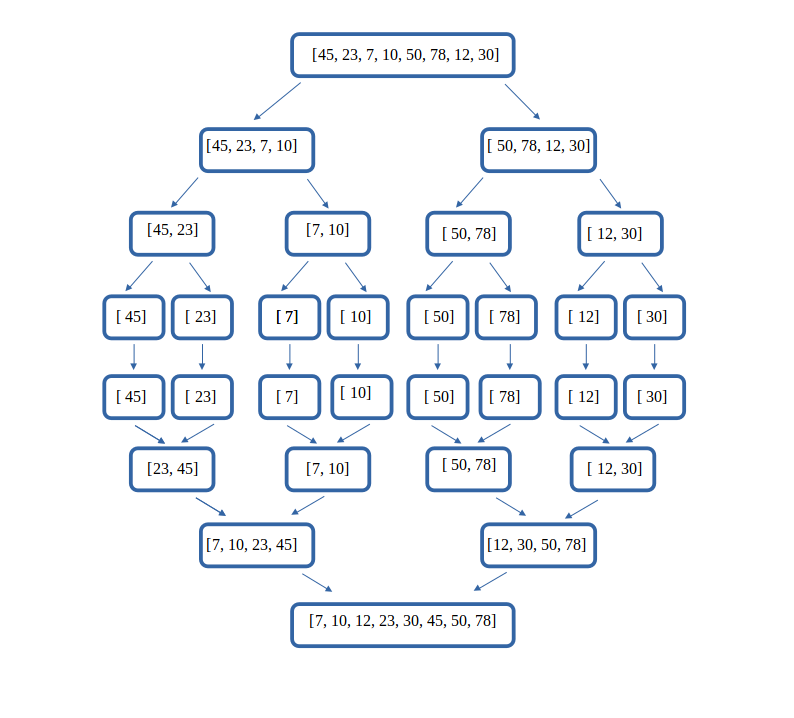
02° Réaliser sur papier le tri fusion du tableau suivant :
[45, 23, 7, 10, 50, 78, 12, 30]
Pour pouvez vous baser sur un schéma de ce type :
...CORRECTION...
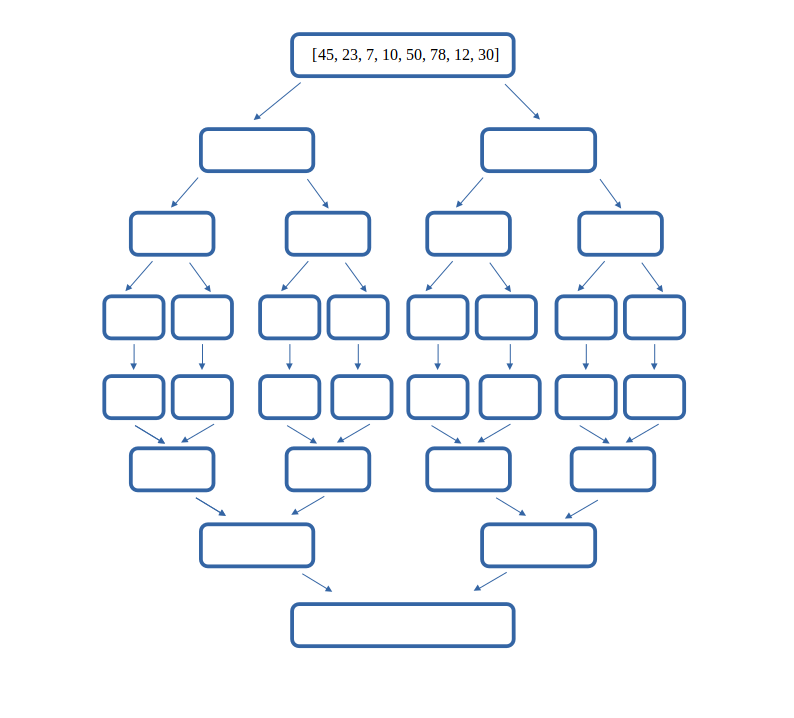
2.1 Coût de la phase DIVISER avec un tableau
On rappelle que nous avons vu trois grands types de listes :
- La liste sous forme d'un couple (tête, queue) non mutable
- La liste sous forme d'une liste contiguë (un tableau statique)
- La liste sous forme d'une liste chaînée (simplement chaînée dans notre cas)
Nous allons nous intéresser au cas du tableau (c'est à dire à une liste contiguë).
03° Quel devrait-être le coût d'une division d'un tableau en deux en imaginant le prototype d'une fonction scinder() de ce type :
scinder (t:tableau) -> (tableau, tableau):
On notera n le nombre de cases du tableau.
- Constant
- Logarithmique
- Linéaire
- Quadratique
...CORRECTION...
Il va falloir créer deux tableaux à partir du tableau initial.
Il faut donc copier les cases une par une. D'où un coût linéaire.
04° Le coût de la première division en deux du tableau est donc linéaire (en 𝞗(n)).
Quel devrait-être
- le nombre d'opérations nécessaires pour scinder le sous-tableau de gauche ?
- le nombre d'opérations nécessaires pour scinder le sous-tableau de droite ?
- le coût de l'opération totale sur cet étage de résolution du problème ?
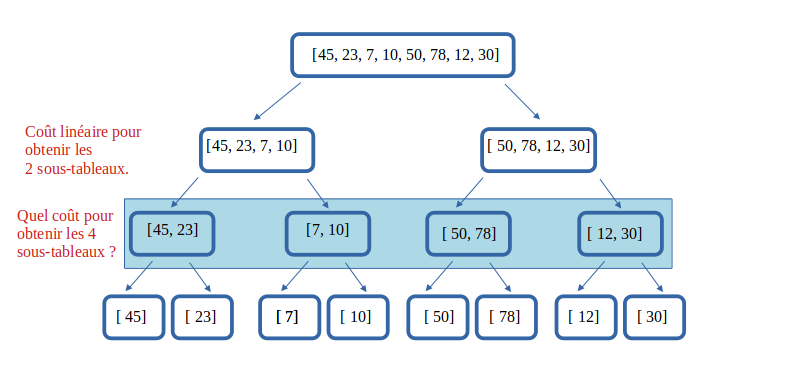
...CORRECTION...
Le tableau de gauche contient n//2 éléments.
L'application de la fonction scinder() sur la partie gauche demande donc n//2 opérations.
De façon similaire, scinder la partie de droite demande également n//2 opérations.
Au total sur cet étage de résolution, on obtient donc n opérations.
En conclusion, on peut donc affirmer que cet étage a également un coût linéaire par rapport au nombre n de cases du tableau initial.
05° Expliquer clairement pourquoi le coût de l'opération visant à obtenir les 8 tableaux à partir des 4 tableaux de l'étage du dessus est également linéaire par rapport au nombre d'éléments du tableau initial.
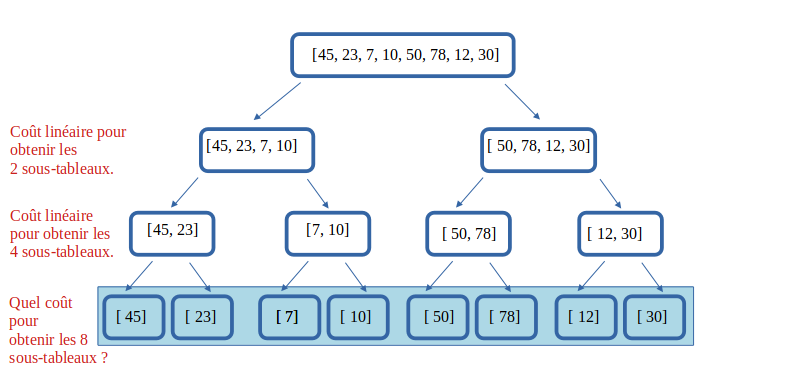
...CORRECTION...
On peut considérer que chacun des 4 tableaux à scinder contient un nombre d'éléments de l'ordre de n//4 éléments.
Au total, puisqu'il y a 4 tableaux de ce type, on obtient un nombre d'opérations lié à 4*n//4 opérations. On peut donc affirmer qu'on aura un nombre d'opérations de l'ordre de n.
En conclusion, on peut donc affirmer que cet étage a également un coût linéaire par rapport au nombre n de cases du tableau initial.
06° Quel est donc le nombre total d'opérations nécessaires pour effectuer la division du tableau total en 8 petits tableaux ?
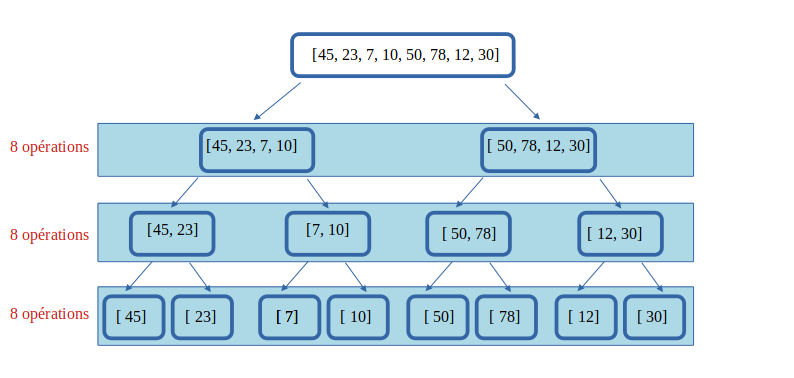
Quel pourraît alors être le coût de cette opération ?
- Logarithmique (avec une complexité en log2(n))
- Linéaire (avec une complexité en n)
- Quasi-linéaire (avec une complexité en n log2(n))
- Quadratique (avec une complexité en n2)
...CORRECTION...
On voit qu'il faut 3*8 soit 24 opérations.
Or, on sait que log2(8) = log2(23) = 3 !
Dans la mesure où on peut écrire que 24 peut être obtenu avec 8*log2(8), la complexité de l'opération de division du tableau en tableaux d'une seule case est quasi-linéaire.
07° Quel est donc le nombre d'opérations nécessaires pour effectuer la division d'un tableau de 16 éléments en 16 petits tableaux ?
...CORRECTION...
Il faut 16 opérations par étage et il y aura 4 étages : 64 opérations.
- Etage 1 : on passe de 16 éléments à 8 éléments par tableau.
- Etage 2 : on passe de 8 éléments à 4 éléments par tableau.
- Etage 3 : on passe de 4 éléments à 2 éléments par tableau.
- Etage 4 : on passe de 2 éléments à 1 élément par tableau.
Or, on sait que log2(16) = log2(24) = 4 !
Dans la mesure où on peut écrire que 64 peut être obtenu avec 16*log2(16), la complexité de l'opération de division du tableau en tableaux d'une seule case est quasi-linéaire.
Conclusion : la phase DIVISER du tri fusion possède un coût quasi-linéaire (avec une complexité en n log2(n)).
2.2 Coût de la phase REGNER
Le coût de la phase REGNER est nulle puisqu'on ne fait rien. On peut donc dire que cette phase est à coût constant.
Il nous reste à voir le coût de la phase COMBINER qui consiste à obtenir un tableau trié à partir de deux sous-tableaux triés.
2.3 Coût de la phase COMBINER
- Phase COMBINER : on fusionne alors facilement nos deux tableaux triés : le plus petit élément de chaque tableau est au début du tableau. Trier les éléments des deux tableaux revient à lire deux valeurs à chaque étape et faire leur comparaison.
Si n et m sont les longueurs des deux listes triées, on peut donc dire que l'étape COMBINER est à coût linéaire (en 𝞗(n+m)).
08° Quel va être le coût de la fusion des deux derniers sous-tableaux en un tableau trié en fonction de n , le nombre de cases du tableau initial ?
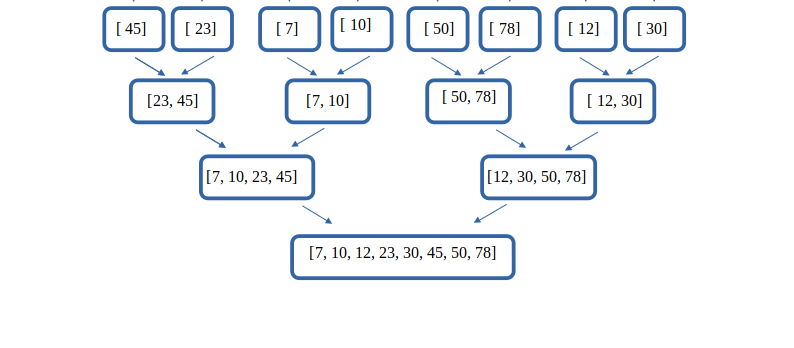
...CORRECTION...
- Nous avons deux sous-tableaux dont l'ordre de grandeur du nombre d'éléments est n//2.
- Nous avons vu que la fusion était effectuée à coût linéaire.
(1)+(2) implique que l'ordre de grandeurs de opérations nécessaires pour former le grand tableau est fonction de 2*n//2.
On peut en déduire que cet étage de déroulement se fait à coût linéaire par rapport à n.
09° Quel va être le coût de la fusion des quatre derniers sous-tableaux en deux tableaux triés en fonction de n , le nombre de cases du tableau initial ?
...CORRECTION...
- Nous avons quatre sous-tableaux dont l'ordre de grandeur du nombre d'éléments est n//4.
- Nous avons vu que la fusion était effectuée à coût linéaire.
(1)+(2) implique que l'ordre de grandeurs de opérations nécessaires pour former les deux tableaux est fonction de 4*n//4.
On peut en déduire que cet étage de déroulement se fait à coût linéaire par rapport à n.
10° Combien d'opérations au total pour fusionner les 8 sous-tableaux en un seul tableau trié ?
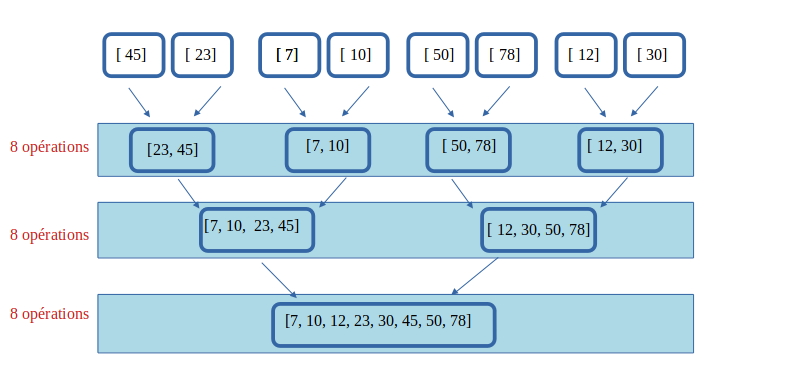
Quel pourraît alors être le coût de cette opération ?
- Logarithmique (avec une complexité en log2(n))
- Linéaire (avec une complexité en n)
- Quasi-linéaire (avec une complexité en n log2(n))
- Quadratique (avec une complexité en n2)
...CORRECTION...
Il faut 8 opérations par étage et il y aura 3 étages.
- Etage 1 : on passe de 1 élément par tableau à 2 éléments par tableau.
- Etage 2 : on passe de 2 éléments par tableau à 4 éléments par tableau.
- Etage 3 : on passe de 4 éléments par tableau à 8 éléments par tableau.
Or, on sait que log2(8) = log2(23) = 3 !
Dans la mesure où on peut écrire que 24 peut être obtenu avec 8*log2(8), la complexité de l'opération de fusion des tableaus en un tableau unique est quasi-linéaire.
11° Combien d'opérations au total pour fusionner 16 sous-tableaux en un seul tableau trié ?
Quel pourraît alors être le coût de cette opération ?
- Logarithmique (avec une complexité en log2(n))
- Linéaire (avec une complexité en n)
- Quasi-linéaire (avec une complexité en n log2(n))
- Quadratique (avec une complexité en n2)
...CORRECTION...
Il faut 16 opérations par étage et il y aura 4 étages.
- Etage 1 : on passe de 1 élément par tableau à 2 éléments par tableau.
- Etage 2 : on passe de 2 éléments par tableau à 4 éléments par tableau.
- Etage 3 : on passe de 4 éléments par tableau à 8 éléments par tableau.
- Etage 3 : on passe de 8 éléments par tableau à 16 éléments par tableau.
Or, on sait que log2(16) = log2(24) = 4 !
Dans la mesure où on peut écrire que 64 peut être obtenu avec 16*log2(16), le coût de l'opération de fusion des tableaux en un tableau unique est quasi-linéaire.
2.4 Coût du tri fusion sur un tableau
Coût du tri fusion sur un tableau
On peut décomposer le tri fusion en 3 étapes selon le principe de diviser pour régner.
- Phase DIVISER : on scinde la liste en deux récursivement
- Phase REGNER : on obtient une liste triée de 1 élément
- Phase COMBINER : on fusionne les liste deux à deux jusqu'à obtenir la liste triée finale
Sur un tableau initial de n éléments, le coût des étapes est :
- Phase DIVISER : coût quasi-linéaire (avec une complexité en n log2(n))
- Phase REGNER : coût constant (et même nul ici)
- Phase COMBINER : coût quasi-linéaire (avec une complexité en n log2(n))
Au total, le tri fusion d'un tableau est donc à coût quasi-linéaire.
3 - Tri fusion avec Python
Nous allons travaillé avec deux implémentations en tableaux. Le premier tri fonctionnera en renvoyant un nouveau tableau trié et le deuxième tri en modifiant le tableau en place.
Tri fusion renvoyant une copie triée du tableau initial
12° Compléter la fonction fusionner() de façon à implémenter l'algorithme de fusion de deux tableaux statiques triés. Il doit fournir en sortie un nouveau tableau statique trié comportant les éléments des deux précédents.
| t1 = [13, 18, 89, 100] | ⇒ | FUSIONNER | ⇒ | |
| et | t = [3, 8, 13, 18, 50, 80, 89, 100] | |||
| t2 = [3, 8, 50, 80] |
Le fonctionnement global par étape :
- Etape 1 : Création d'un tableau t_fusion ayant la bonne taille pour récupérer la fusion
- Etape 2 : Initialisation des indices permettant de connaitre la case qu'on va remplir dans t_fusion et des indices de début, de fin et de la case à lire dans les deux sous-tableaux
- Etape 3 : Remplissage de t_fusion jusqu'à ce que l'un des deux sous-tableaux soit entièrement lu
- Etape 4 : Remplissage de t_fusion avec le sous-tableau restant
- Etape 5 : On renvoie le tableau t_fusion
Voici le prototype :
def fusionner(t1:list, t2:list) -> list:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51 | |
...CORRECTION...
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51 | |
13° Compléter la fonction scinder() de façon à implémenter l'algorithme de division d'un tableau statique en deux tableaux. Il doit fournir en sortie un couple (tuple à 2 éléments) comportant deux tableaux issus des parties gauche et droite du tableau de base.
| ⇒ | SCINDER | ⇒ | ||
| t = [30, 8, 100, 50, 55] | ([30, 8], [100, 50, 55]) | |||
Le fonctionnement global par étape :
- Etape 1 : On récupère les 3 indices importants du tableau t : l'indice de la première case, de la dernière case et de la case du milieu.
- Etape 2 : On crée les deux sous-tableaux gauche et droite par compréhension (ou Slicing mais hors programme de NSI)
- Etape 3 : On renvoie les deux tableaux à l'intérieur d'un tuple puisqu'une fonction ne peut renvoyer qu'une unique réponse.
Voici le prototype :
def scinder(t:list) -> tuple(list, list):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29 | |
...CORRECTION...
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29 | |
14° Compléter la fonction trier() de façon à implémenter l'algorithme du tri fusion d'un tableau statique.
| ⇒ | TRIER | ⇒ | ||
| t = [30, 8, 100, 50, 55] | [8, 30, 50, 55, 100] | |||
Le fonctionnement global :
- Etape DIVISER : on utilise la fonction scinder() pour obtenir deux sous-tableaux plus petits.
- Etape REGNER : lorsqu'on obtient un sous-tableau de moins de 2 cases, on sait que le sous-tableau est trié.
- Etape COMBINER : on utilise la fonction fusionner() pour fusionner deux sous-tableaux plus petits.
Dans le cadre d'une fonction récursive, cela donne donc :
- CAS DE BASE : si le tableau reçu comporte 1 élément ou moins, on renvoie une copie exacte.
- CAS RECURSIF : on divise le tableau en deux et on renvoie la fusion de la partie gauche triée avec trier() et la partie droite triée avec trier()
Voici le prototype :
def trier(t:list) -> list:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101 | |
...CORRECTION...
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101 | |
Tri fusion modifiant le tableau statique en place
15° Compléter la fonction fusionner() de façon à implémenter l'algorithme de fusion de deux sous-tableaux triés à l'intérieur d'un tableau t. Il ne fournir rien en sortie puisqu'il modifie le tableau en place.
On doit fournir en entrée :
- la référence du tableau t
- L'indice d1 et f1 du début et de la fin du sous-tableau 1 (indices inclus)
- L'indice f2 de la fin du sous-tableau 2 (indices inclus). On ne donne pas d2 car cet indice vaut nécessairement f1 + 1
| t = [3, 8, 13, 18, 50, 100, 80, 89] | ⇒ | FUSIONNER | ⇒ | |
| d1 = 4, f1 = 5 | VIDE | |||
| f2 = 7 |
Le tableau est alors devenu t = [3, 8, 13, 18, 50, 80, 89, 100]
Le fonctionnement global par étape :
- Etape 1 : Création d'un tableau t_fusion ayant la bonne taille pour récupérer temporairement la fusion
- Etape 2 : Initialisation des indices permettant de connaitre la case qu'on va remplir dans t_fusion et des indices de début, de fin et de la case à lire dans les deux sous-tableaux
- Etape 3 : Remplissage de t_fusion jusqu'à ce que l'un des deux sous-tableaux soit entièrement lu
- Etape 4 : Remplissage de t_fusion avec le sous-tableau restant
- Etape 5 : On modifiant maintenant les cases correspondantes du tableau t à l'aide des cases du tableau t_fusion
Voici le prototype :
def fusionner(t:list, d1:int, f1:int, f2:int) -> None:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57 | |
...CORRECTION...
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57 | |
Il existe plusieurs façons différentes de réaliser la fusion. Le but n'est pas ici de les étudier une par une.
16° Expliquer en quelques phrases comment fonctionne la fonction lancer_tri_fusion() puis la fonction trier() dans cette version mutable.
Ecrire ensuite la pile d'appels lorsqu'on lance lancer_tri_fusion() sur le tableau [10, 30, 20, 40, 15, 60].
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105 | |
4 - FAQ
On peut démontrer que le coût est quasi-linéaire sur le tri fusion ?
Oui, mais c'est hors programme car on utilise la démonstration par récurrence, vue en spé Maths en 1er.
Vous pouvez néanmoins la comprendre assez facilement si vous avez suivi la 1er NSI puisque cette démonstration est très proche de la preuve de correction des algorithmes.
Preuve de correction et invariant
Définitions
La preuve de correction d'un algorithme permet d'affirmer
- qu'il fournit toujours une réponse correcte
- sur toutes les entrées valides qu'on lui fournit.
Pour faire la preuve de correction d'un algorithme, il faut trouver un INVARIANT : une propriété P vérifiable qui reste vraie lors des différentes étapes de l'algorithme.
Un INVARIANT DE BOUCLE est une propriété VRAIE à chaque début de tour, juste avant l'exécution de la première instruction de la boucle.
Cet invariant permettra de prouver que le résultat final après exécution est bien le résultat attendu.
Malheureusement, il n'y a pas de méthodologie automatique miraculeuse pour trouver cet invariant. Il faut réfléchir et tenter des choses, comme avec toute démonstration.
Démonstration en 3 phases : Initialisation-Conservation-Terminaison
Une fois qu'on dispose d'un INVARIANT P, la démonstration se fait en trois temps.
- Phase d'initialisation : P0 est VRAI
- Phase de conservation : Pk ➡ Pk+1
- Hypothèse de départ :
- Déroulement du tour de boucle (k+1) jusqu'au début du prochain
- On peut donc écrire Pk ➡ Pk+1
- Phase de terminaison
On doit prouver que l'INVARIANT est VRAI lorsqu'on commence le premier tour de boucle mais sans l'avoir réalisé en entier. On a donc fait 0 tour en entier.
Le plus souvent, cette partie est triviale. Mais pas toujours...
SI P est vrai après k tours de boucles, ALORS P sera encore vrai en ayant fait un tour de boucles supplémentaire.
On fait l'hypothèse qu'on a fait k tours de boucles et qu'on est au début du tour k+1. L'INVARIANT Pk est donc considéré juste.
On doit montrer qu'en réalisant ce tour complétement jusqu'au début du prochain, l'invariant P reste vrai à la fin de cette boucle. On aura donc fait k+1 tours de boucle complet, Pk+1 serait encore vérifiée.
On se place dans le cadre d'un tour qui est suivi d'un autre tour. On ne se place pas dans le cadre de la toute dernière boucle ici. On boucle, point.
On doit y prouver qu'à la fin du dernier tour, on obtient la situation voulue. Ni trop tôt, ni trop tard. C'est pour cela qu'on nomme cette partie la phase de terminaison, à ne pas confondre avec la preuve de terminaison.
P0 ➡ P1 ➡ P2 ➡ P3... ➡ Pfinal
La démonstration par récurrence est assez proche puisqu'on fait la même chose sans vérifier la dernière étape : il ne s'agit pas de vérifier qu'on s'arrête au bon endroit comme un algorithme mais juste qu'une propriété est vraie.
- Etape d'initialisation
- On montre que notre propriété P est vraie au départ : P0 est VRAI.
- Etape d'hérédité (qui se nomme étape de conservation lors d'une preuve de correction)
- On fait l'hypothèse que P est vraie à l'étape k.
- On doit démontrer que dans ce cas, P est nécessairement vraie à l'étape k+1
- On peut donc écrire Pk ➡ Pk+1
- Conclusion (qui se nomme terminaison lors d'une preuve de correction)
- Il suffit d'énoncer que puisque la propriété est vraie au départ et que le fait qu'elle soit vraie à une étape implique qu'elle est vraie à l'étape suivante alors elle est nécessairement vraie à n'importe quelle étape k, k étant un entier naturel.
Sur le cas du tri fusion, montrons que le coût est bien quasi-linéaire.
Notre propriété P est donc que la complexité de l'algoritmhe est n log2(n).
Etape d'initialisation
Si le tableau ne contient qu'un élément (n=1=20), il ne faut aucune comparaison pour résoudre le problème.
Or 1 log2(1) = 1 log2(20) = 0.
P0 est donc VRAI.
Etape d'hérédité (qui se nomme étape de conservation lors d'une preuve de correction)
On considère par hypothèse que la formule est vraie pour n= 2k éléments.
Pk est donc VRAI par hypothèse.
On considère maintenant que nous avons 2k+1 éléments.
Le nouveau nombre d'éléments est donc égal à 2*2k puisque
2*2k = 21*2k = 2k+1
Trier un tableau de 2k+1 éléments revient donc à trier deux tableaux de 2k élements puis à rajouter 2k+1 opérations pour fusionner les deux tableaux en un seul tableau (nous avons montrer que le coût de la fusion était linéaire).
Le nombre d'opérations estimées est donc :
2 * 2k * log2(2k) + 2k+1
2k+1 * log2(2k) + 2k+1 * 1
2k+1 * (log2(2k) + 1)
2k+1 * (k + 1)
2k+1 * (log2(2k+1))
Ce qui est exactement la propriété Pk+1.
On vient donc de montrer que si Pk est vraie, alors Pk+1 est vraie également.
Conclusion
Puisque l'intialisation est vraie et que l'hérédité est vraie, alors la propriété P est vraie quelque soit la valeur de k.
P est donc vraie : le coût de l'algorithme de tri fusion est bien quasi-linéaire.
C'est quoi le slicing ?
Déjà, ce n'est pas au programme de NSI. Juste une facilité d'écriture, bien pratique, présente dans pas mal de langages mais qui rajoute une couche de connaissances inutiles puisqu'on vous demande de savoir manipuler la création par compréhension.
Une facilté de Python et d'autres langages pour récupérer des bouts de tableaux par exemple.
Voici plusieurs exemples où je montre d'abord comment faire avec compréhension puis en utilisant le slicing (le "tranchage" en anglais).
>>> t = [10, 50, 30, 20, 60]
>>> g = [t[i] for i in range(0, 4)]
>>> g
[10, 50, 30, 20]
>>> g = [t[i] for i in range(4)]
>>> g
[10, 50, 30, 20]
>>> g = t[0:4]
>>> g
[10, 50, 30, 20]
>>> g = t[:4]
>>> g
[10, 50, 30, 20]
Comme vous pouvez le voir, on obtient une notation plus légère qu'avec le compréhension pour le même effet. On peut se passer de donner la valeur initiale s'il s'agit de la valeur 0 et la valeur finale est exclue comme avec range.
Là où c'est pratique, c'est qu'on peut également se passer de la valeur finale. Du coup, on peut faire des copies facilement. Mais on peut faire des copies aussi avec de la compréhension, avec la fonction native list() ou avec la méthode copy() :
>>> t = [10, 50, 30, 20, 60]
>>> c = t[:]
>>> c
[10, 50, 30, 20, 60]
>>> c = t[0:4]
>>> c
[10, 50, 30, 20]
>>> c = [v for v in t]
>>> c
[10, 50, 30, 20, 60]
>>> c = list(t)
>>> c
[10, 50, 30, 20, 60]
>>> c = t.copy()
>>> c
[10, 50, 30, 20, 60]
Pour récupérer les côtés gauche et droite d'un tableau, on peut donc juste faire ceci une fois qu'on a l'habitude :
Pour finir, nous pouvons les utiliser pour diviser facilement un tableau en deux, même si c'est le côté droit qui récupère l'élément supplémentaire éventuel :
>>> t = [10, 50, 30, 20, 60]
>>> g = t[:len(t)//2]
>>> g
[10, 30]
>>> d = t[len(t)//2:]
>>> d
[20, 40, 15]
En conclusion, le slicing est pratique mais totalement dispensable. Ne l'utilisez pas dans vos programmes, préférez les constructions par compréhension, plus explicites et surtout officiellement au programme.
Activité publiée le 30 03 2021
Dernière modification : 30 03 2021
Auteur : ows. h.