25 - Programmation dynamique
Nous avons déjà rencontré plusieurs façons de résoudre un problème.
- Résolution par force brute : on y va franchement, on calcule tout, quitte à calculer les choses plusieurs fois. Calculer, calculer, calculer...
- Résolution par la stratégie gloutonne : on résoud le problème en ne s'intéressant qu'à un problème local immédiat. Cette sous-réponse reste définitive et va mener à un autre sous-problème et vers UNE solution finale, pas nécessairement la meilleure solution. Choisir et réduire, choisir et réduire, choisir et réduire, ...
- Résolution par la stratégie Diviser pour Règner : on résoud le problème en le découpant en plusieurs sous-problèmes plus petits. On résoud chaque sous-problème puis on combine les résultats pour répondre à la question. Diviser - Régner - Combiner.

Imaginons qu'on veuille faire tourner Tux, la mascote de Linux :

On peut calculer les positions des pixels en faisant un peu de mathématiques, ou on peut utiliser la méthode diviser pour régner. Regardez le résultat :
On divise Tux en quatre zones et on les décale simplement dans le sens horaire :


On divise à nouveau chacune des 4 zones en 16 sous-zones. Et dans chaque zone, on décale les sous-zones dans le sens horaire :

On divise à nouveau chacune des 16 sous-zones en 4, soit 64 sous-sous-zones. Et dans chaque sous-zone, on décale les sous-sous-zones dans le sens horaire :

Et on continue :


Et on continue :


Et on continue :


Et encore et encore jusqu'à arriver à des sous-zones qui sont constituées uniquement de ... 1 pixel. Du coup, pas besoin de faire de rotation...
Et on continue :


Nouvelle stratégie aujourd'hui : la programmation dynamique. En image, ça donnera ceci :

Et en fin d'activité, vous comprendrez mieux comment je compte me reconvertir dans la production de planches de bois :

Logiciel nécessaire pour l'activité : -
Prérequis : au moins une autre stratégie de résolution : gloutonne ou diviser pour régner
Evaluation ✎ :
Documents de cours : open document ou pdf
1 - Limite des techniques vues jusqu'à présent
Imaginons que vous vouliez savoir s'il faut rester dans une file d'attente pour acheter une place de concert, ou si ce n'est plus la peine.
Seule manière de savoir : lire l'attitude des deux personnes juste devant vous.
Il faudra associer une valeur à l'incertitude des personnes d'obtenir une place pour ce concert.
- 0, c'est la certitude d'avoir une place : on est au gichet et on paye.
- 1 pourrait correspondre au fait de voir la personne qui vient de s'acheter la place.
- ect... Plus cette valeur est grande, plus l'incertitude grandit.
- f(0) = 0 pour la personne d'indice 0 dans la file. Elle sait qu'elle va avoir sa place.
- f(1) = 1 pour la personne d'indice 1 juste derrière dans la file

Pour modéliser l'attitude des suivants, partons sur le fait qu'on additionne les incertitudes des deux personnes devant nous :
- f(2) = f(1) + f(0)
- f(3) = f(2) + f(1)
- f(4) = f(3) + f(2)
- f(5) = f(4) + f(3)
- ...
Cela se résume par formule suivante :
f(n) = f(n - 1) + f(n - 2)
01° Calculer f(5) en justifiant vos calculs.
02° Compléter la fonction Python f() dont le prototype est fourni pour qu'elle renvoie la bonne valeur d'incertitude d'achat du billet en fonction de la position n de la personne dans la file d'attente.
On impose la récursivité : il faut commencer par se demander quels sont les cas de base, puis de demander comment travailler s'il ne s'agit pas d'un cas de base.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 | |
...CORRECTION...
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27 | |
03° Lancer les appels suivants pour voir l'évolution du temps de réponse :
>>> f(5)
5
>>> f(10)
55
>>> f(20)
6765
>>> f(30)
832040
>>> f(40)
102334155
Rapide ou pas ?
Regardons maintenant pourquoi cela devient rapidement si long avant que votre fonction ne réponde.
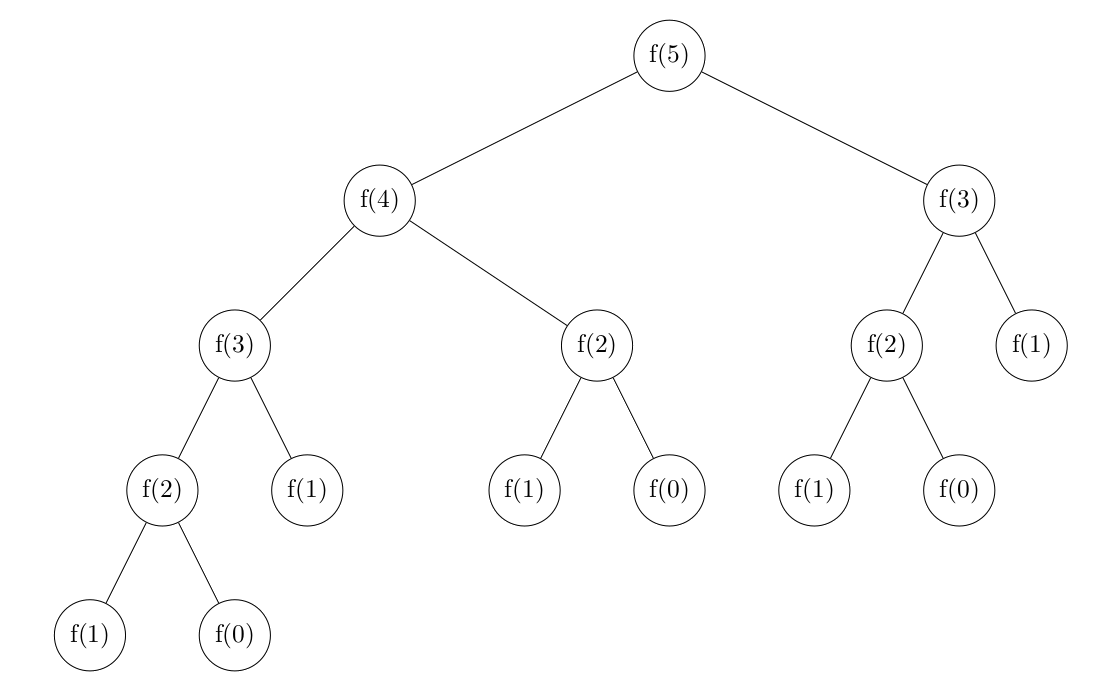
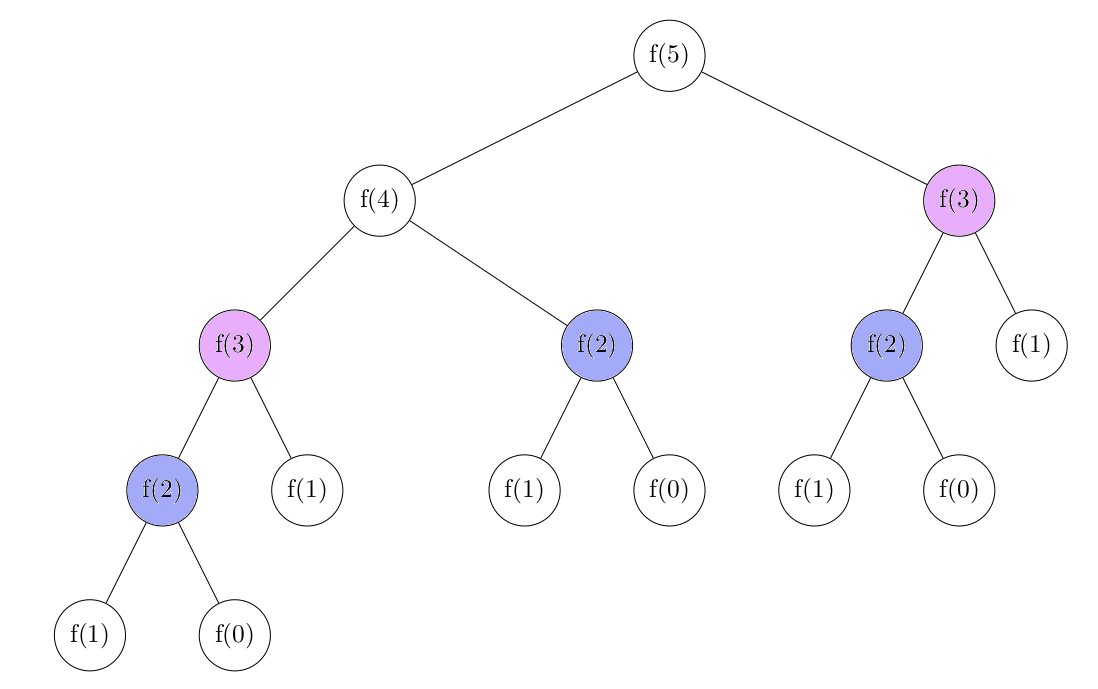
04° Combien d'appels à la fonction f() va-t-on faire pour calculer f(2) ? Combien d'appels pour calculer f(3) ? Combien d'appels pour calculer f(4) ? Combien d'appels pour calculer f(5) ?
...CORRECTION...
Il suffit de compter les noeuds.
L'appel f(2) engendre 3 appels au total.
L'appel f(3) engendre 5 appels au total.
L'appel f(4) engendre 9 appels au total.
L'appel f(5) engendre 15 appels au total.
05° Si on nomme nb_appels(n) le nombre d'appels nécessaires pour calculer la fonction f(n), quelle formule récursive peut-on utiliser pour calculer ce nombre d'appels avec comme précondition n > 1 ?
nb_appels(n) = ...
Calculer alors ce nombre d'appels pour f(6), f(7) et f(8).
...CORRECTION...
Il faut se demander comment faire chaque appel de fonction peut faire le travail en utilisant les autres....
Chaque fonction calculant le nombre d'appels devra renvoyer :
return 1 + nb_appels(n - 1) + nb_appels(n - 2)
De façon plus mathématique, on peut écrire :
nb_appels(n) = 1 + nb_appels(n - 1) + nb_appels(n - 2)
f(6) provoque donc 1 + 15 + 9 appels, soit 25 appels car
- f(5) provoque 15 appels et
- f(4) provoque 9 appels.
f(7) provoque donc 1 + 25 + 15 appels, soit 41 appels car
- f(5) provoque 25 appels et
- f(4) provoque 15 appels.
f(8) provoque donc 1 + 41 + 25 appels, soit 67 appels car
- f(7) provoque 41 appels et
- f(6) provoque 25 appels.
Pour vous donner une idée des valeurs suivantes :
f(9) provoque donc 1 + 67 + 41 appels, soit 109 appels car
- f(8) provoque 67 appels et
- f(7) provoque 41 appels.
f(10) provoque donc 1 + 109 + 67 appels, soit 177 appels car
- f(9) provoque 109 appels et
- f(8) provoque 67 appels.
f(11) provoque donc 1 + 177 + 109 appels, soit 287 appels car
- f(10) provoque 177 appels et
- f(9) provoque 109 appels.
f(12) provoque donc 1 + 287 + 177 appels, soit 465 appels car
- f(11) provoque 287 appels et
- f(10) provoque 177 appels.
Comme vous pouvez le voir cela augmente dangereusement vite...
Si on désire faire compter automatiquement le nombre d'appels avant la résolution du problème posé, il va falloir modifier un peu le programme.
Nous allons rajouter un paramètre optionnel de type mutable de façon à ce que c augmente de 1 à chaque fois qu'on lance un appel à f(). De cette façon, nous aurons bien le nombre total d'appels.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26 | |
06-A° Placer la nouvelle fonction en mémoire. L'évolution du nombre d'appels semble-t-elle linéaire ? Que risque-t-il de se passer lorsqu'on voudra lancer le calcul avec un paramètre de grande valeur ?
>>> f(5)
1
2
...
15
5
>>> f(10)
1
2
...
177
55
>>> f(20)
1
2
...
21891
6765
06-B° Qu'est-ce qui ralentit fortement vraiment ce programme avec traces pour le moment ?
...CORRECTION...
Ce sont les appels à print().
Dès qu'on programme avec l'optique de réaliser un programme rapide, il faut :
- Savoir évaluer le coût de votre fonction (constant, logarithmique, linéaire, quasi-linéaire, quadratique...
- Eviter de faire des appels en lecture/écriture avec l'extérieur (avec print() pour l'écran ou open()/write() pour les fichiers) car toutes instructions nécessitant de sortir du processeur demande énormément de temps, indépendamment du coût par rapport au nombre de données à traiter. Nous l'avions vu dans la partie Architecture.
06-C° Une autre façon de créer ce compteur : utiliser une fonction auxiliaire, locale à la fonction f().
Expliquer comment fonctionne maintenant la fonction f() qui utilise la fonction auxiliaire aux().
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27 | |
CONCLUSION TEMPORAIRE
On vient de voir que la force brute ne fonctionne pas dès que l'argument envoyé dépasse environ 30.
On ne peut pas utiliser la stratégie gloutonne car il ne s'agit pas d'un problème d'optimisation : il n'y a qu'une seule bonne réponse et pas plusieurs solutions plus ou moins bonnes.
On ne peut pas non plus utiliser la stratégie diviser pour régner car en réduisant le problème f(n) en deux sous-problèmes f(n-1) et f(n-2), on n'obtient pas deux sous-problèmes indépendants l'un de l'autre : le résultat de f(n-1) dépend en partie de f(n-2) !
Nous allons donc voir comment résoudre cette nouvelle catégorie de problème en utilisant une nouvelle statégie : la stratégie de la programmation dynamique.
2 - Programmation dynamique
Pour réduire les calculs, nous allons rajouter de l'intelligence plutôt que de passer par force brute. C'est là qu'intervient la programmation dynamique :

Principe général :
On analyse le problème de la recherche des sous-solutions imbriquées les unes dans les autres et on se demande quels sont les sous-problèmes à résoudre avant les autres.
On met en mémoire chaque sous-solution dès qu'on l'obtient. De cette façon, une fois que f(3) aura été calculée une première fois, il suffira d'aller relire le résultat plutôt que de relancer le vrai calcul !
Sur notre exemple avec f(5), cela donnerait donc l'arbre d'appels suivant :
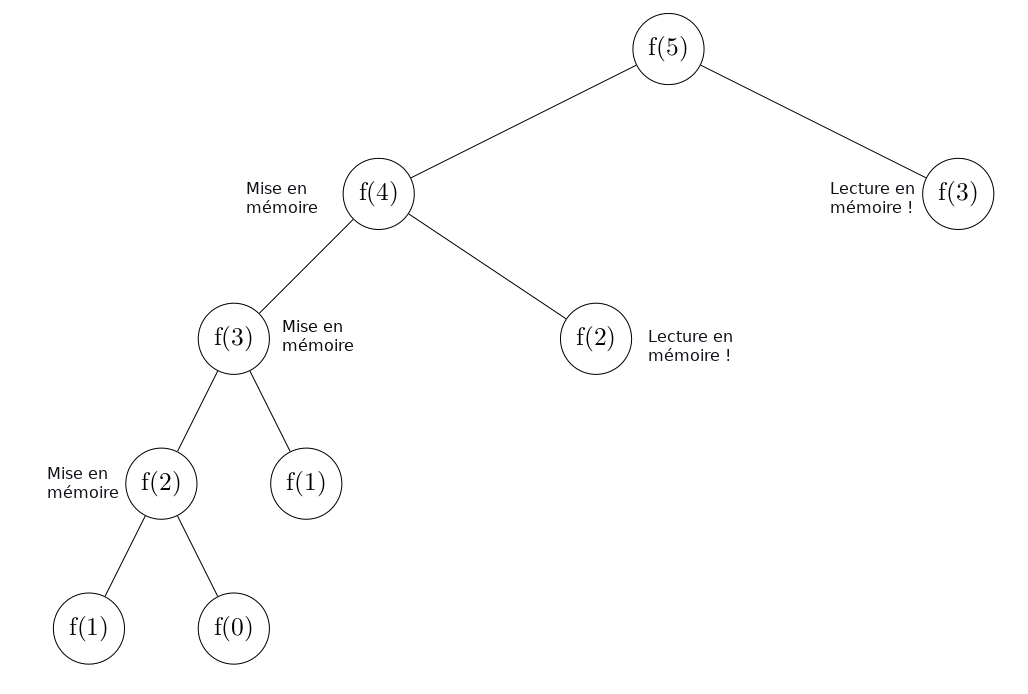
Pour rappel, sans stockage des résultats, nous avions l'arbre suivant par notre calcul naïf :

07° Répondre aux questions suivantes en analysant l'arbre des appels :

- Combien d'appels au total cette fois pour f(5) ?
- Après l'appel initial à f(5), faut-il calculer f(4) ou plutôt f(2) ?
- Que faut-il faire ensuite ?
Pour réaliser cela, nous allons donc devoir stocker les résultats des sous-problèmes intermédiaires dans une mémoire temporaire qu'on nomme mémoire-cache. On peut prendre n'importe quelle structure de données mutable en Python.
- Tableau via le type list : avantage de la rapidité si on peut facilement attribuer un numéro à chaque sous-problème.
- Dictionnaire via le type dict sinon.
08° Répondre à ces trois questions.
- Traduire en Français les lignes 3 à 8.
- Expliquer ce que va contenir le tableau-mémoire-cache m une fois arrivé en ligne 10.
- Pourquoi avoir mis n+2 ligne 6 ? Quel est le cas problématique qui nous oblige à noter (n+2) plutôt que simplement (n+1) pour créer le tableau avec des indices allant de 0 à n ?
1
2
3
4
5
6
7
8
9
10
11 | |
...CORRECTION...
- Traduction
- m = [0, 1, None, None, None...]
- Lorsqu'on désire calculer f(n), il faut stocker les valeurs de f(x) pour x allant de 0 à n. Il faut donc (n+1) cases. Normalement, range(n+1) renvoie un itérateur [0, 1, 2, ..., n] et cela pourrait suffire. Sauf pour UN cas : celui de f(0). Si n reçu vaut 0, alors on va créer uniquement un tableau de 1 cases : range(0+1) ne renvoie qu'une valeur et on aurait alors un tableau de 1 case : [None]. La ligne 7 ne pose pas de problème mais la ligne 8 oui : la case 1 n'existerait pas. Nous sommes donc obligé de créer un tableau avec une case en plus (pas très grave d'un point de vue coût) qui ne servira que pour l'appel à f(0).
L3 : Vérifie que n soit bien supérieur ou égal à 0. Si ce n'est pas le cas, lève une Exception.
L6 : Crée un tableau-mémoire de n+2 cases contenant toutes None.
L7-L8 : Remplis la mémoire avec les valeurs déjà connues pour f(0)=0 et f(1)=1.
Remarque : nous aurions pu agir différemment : renvoyer 0 si n=0, 1 si n=1 et ne créer la mémoire avec range(n+1) que pour les autres cas.
09° Compléter la fonction f() pour créer la planification des appels en mode ascendant (croissant) : on calcule et place dans la mémoire-cache m d'abord "f"(2) puis "f"(3)... jusqu'à obtenir celui qui vous intéresse.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15 | |
...CORRECTION...
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15 | |
10° Utiliser maintenant notre fonction pour vérifier qu'on puisse bien calculer f(40) ou plus.
>>> f(40)
?
>>> f(100)
?
>>> f(1000)
?
>>> f(10000)
?
Rapide ou pas ?
Question : quel est le coût de cette fonction en fonction de n ?
...CORRECTION...
- Ligne 6 : Coût linéaire car on crée un tableau de n+2 cases.
- Ligne 7 et ligne 8 : coût constant (accès à une case en RAM).
- Ligne 11-12 : on réalise une boucle liée au nombre de cases dans la mémoire et donc à n et la ligne 12 est à coût constant puisqu'il ne s'agit que d'accès à des cases mémoires en RAM. On a donc O(n*1) = O(n). La boucle est donc à coût linéaire.
- Ligne 15 : coût constant.
Au total sur l'analyse asymptotique : O(n+1+n+1) = O(n). Coût linéaire.
11° Traduire en Français les lignes de votre fonction (ou de la correction fournie si vous avez bloqué).
...CORRECTION...
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15 | |
Programmation dynamique
Vocabulaire
Le mot Programmer s'entend ici sous le sens Planifier, Prévoir. Il n'y aucun lien avec le mot "coder".
Domaine d'utilisation
La stratégie de la programmation dynamique est utilisée lorsqu'on veut résoudre un problème
- dont les sous-problèmes sont interdépendants (par exemple f(9) et f(10) vont devoir faire intervenir f(5) tous les deux)
- dont la solution d'un sous-problème doit être utilisée pour résoudre le problème plus global (par exemple la solution de f(9) est utilisée pour trouver la solution de f(10))
Principe
La stratégie de la programmation dynamique consiste à planifier l'ordre de résolution des différents résultats intermédiaires et les mémoriser pour ne jamais refaire deux fois le même calcul.
A chaque fois qu'une sous-solution est trouvée, on l'enregistre dans une mémoire-cache de façon à pouvoir utiliser à nouveau directement le résultat à coût constant lors de la résolution d'un autre sous-problème.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15 | |
Quelques éléments supplémentaires
Cette stratégie a été introduite par Bellman, dans les années 1950, pour résoudre des problème d’optimisation.
On parvient ainsi à réduire la complexité temporelle au détriment de la complexité en espace-mémoire : on utilise de la mémoire pour éviter de reproduire de nombreuses fois le même calcul.
Il faut réflechir !
Oui et parfois, c'est d'ailleurs assez compliqué de trouver l'ordre de résolution à planifier. Si on ne parvient pas à trouver une méthode qui fonctionne à chaque fois, pas de panique : nous verrons dans la dernière partie une technique basée uniquement sur la mémoïsation, sans planifier directement les calculs. On lance et on mémoïse au fil de l'eau.
3 - Problème de la découpe
Voici un nouveau problème où encore une fois l'informatique intervient dans un domaine qui semble bien éloigné de l'informatique.

Une scierie récupère des troncs d'arbre de 10 mètres et plus pour en faire des planches.
Voici le prix des planches entières en fonction de la longueur de la planche :
| Longueur (m) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Prix | 1 | 5 | 8 | 9 | 10 | 17 | 17 | 20 | 24 | 30 |
Exemple : voici les différents choix qui s'offrent à nous pour des planches de 4m :
On vend une planche d'exactement 1m et on voit comment vendre au mieux les 3m restants
- 9 euros avec 🏿 et 🏾🏾🏾
- 7 euros avec 🏿 et 🏾🏾+🏾
- 7 euros avec 🏿 et 🏾+🏾🏾
- 4 euros avec 🏿 et 🏾+🏾+🏾
22 possibilités de gérer cette découpe. Si on réflechit un peu, on peut voir que si on savait déjà comment gèrer au moins les 3m, nous n'aurions pas eu besoin de tester toutes les possibilités.
On vend une planche d'exactement 2m et on voit comment vendre au mieux les 2m restants
- 10 euros avec 🏿🏿 et 🏾🏾
- 7 euros avec 🏿🏿 et 🏾+🏾
21 possibilités de gérer cette découpe.
On vend une planche d'exactement 3m et on voit comment vendre au mieux le m restant
- 9 euros avec 🏿🏿🏿 et 🏾
20 possibilité de gérer cette découpe.
On vend directement d'exactement 4m.
- 9 euros avec 🏿🏿🏿🏿
Ce n'est pas une découpe.
Comme on le comprend, tester toutes les possibilités deviendrait rapidement trop long.
On retrouve certaines formules vues notamment sur les arbres binaires :
- Avec 4 m : on a 22 + 21 + 20, soit 23 - 1 possibilités.
- Avec 5 m : on a 23 + 22 + 21 + 20, soit 24 - 1 possibilités.
- Avec 5 m : on a 24 + 23 + 22 + 21 + 20, soit 25 - 1 possibilités.
- Avec 20 m : on a 220 - 1 possibilités (1 048 575).
Or, si on réflechit un peu, on voit qu'on peut faire beaucoup moins de calculs si on tente de vendre une planche de 20 m :
- Vendre une planche de 1m associée à la meilleure vente pour 19m.
- Vendre une planche de 2m associée à la meilleure vente pour 18m.
- Vendre une planche de 3m associée à la meilleure vente pour 17m.
- ...
- Vendre une planche de 19m associée à la meilleure vente pour 1m.
- Vendre une planche de 20m directement.
12° Résolution du problème 2m : quelle est la meilleure découpe à faire pour des planches de 2 mètres pour parvenir à vendre en récupérant le plus d'argent ?
| Longueur (m) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Prix | 1 | 5 | 8 | 9 | 10 | 17 | 17 | 20 | 24 | 30 |
- Couper 1m et vendre deux planches de 1 m
- Vendre une planche de 2m
...CORRECTION...
Pour 2m, on peut faire :
- 1m + (en faisant au mieux pour le m restant), qui ramène 1+1 = 2 euros.
- 2m, qui ramène 5 euros.
Mémorisons qu'avec 2 mètres, le mieux est de ne pas couper la planche et de récupèrer 5 euros.
13° Résolution du problème 3m : quelle est la meilleure découpe à faire pour des planches de 3 mètres ?
| Longueur (m) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Prix | 1 | 5 | 8 | 9 | 10 | 17 | 17 | 20 | 24 | 30 |
Nous allons utiliser le résultat précédent.
- Vendre une planche d'un mètre et faire au mieux pour les deux mètres restants (voir question 12)
- Vendre une planche de 2m et faire au mieux pour le mètre restant
- Vendre directement une planche de 3m
...CORRECTION...
Pour 3m, on peut faire :
- 1m + (en faisant au mieux pour les 2m), qui ramène 1+5 euros = 6 euros (on utilise le meilleur cas pour 2m).
- 2m + (en faisant au mieux pour le m), qui ramène 5+1 euros = 6 euros.
- 3m sans découpe, qui ramène 8 euros.
Mémorisons qu'avec 3 mètres, le mieux est de ne pas couper la planche et de récupèrer 8 euros.
14° Résolution du problème 4m : Quelle est la meilleure découpe à faire pour des planches de 4 mètres ?
| Longueur (m) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Prix | 1 | 5 | 8 | 9 | 10 | 17 | 17 | 20 | 24 | 30 |
Nous allons utiliser le résultat précédent.
- Couper 1m et vendre la planche d'un mètre et faire au mieux pour les trois mètres restants (voir question 13)
- Couper 2m et vendre cette planche de 2m et faire au mieux pour les deux mètres restants (voir question 12)
- Couper 3m et vendre cette planche de 3m et le mètre restant
- Ne pas couper la planche et vendre une planche de 4m
...CORRECTION...
Pour 4m, on peut faire :
- 1m + (en faisant au mieux pour les 3m), ce qui ramène 1 + 8 = 9 euros.
- 2m + (en faisant au mieux pour les 2m), ce qui ramène 5 + 5 = 10 euros.
- 3m + (en faisant au mieux pour le m restant), ce qui ramène 8 + 1 = 9 euros.
- 4m sans découpe, qui ramène 9 euros.
Mémorisons qu'avec 4 mètres, le mieux est de vendre 2m+2m, et de récupèrer 10 euros.
15° Compléter maintenant la fonction meilleure_vente() qui doit renvoyer le meilleur prix de ventes d'une planche de longueur initiale taille, et devra travailler à partir du tableau des prix fourni.
meilleure_vente(prix:list, taille:int) -> int
Cette fonction est basée sur la programmation dynamique : on va d'abord chercher à mémoriser le meilleur prix de vente pour une planche initialement de 2m, puis une planche de 3m puis une planche de 4m...
- Le paramètre prix est le tableau des prix où l'indice de la case doit correspondre à la taille des planches. Notez bien que l'indice 0 DOIT contenir 0 : une planche de 0m rapporte nécessairement 0 euro.
- Le paramètre taille est un entier : il correspond à la taille de la planche (l'unité étant le mètre). Ce paramètre est donc également l'indice permettant de retrouver le prix d'une telle planche entière.
Exemple :
| Indice/Longueur | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Prix | 0 | 1 | 5 | 8 | 9 | 10 | 17 | 17 | 20 | 24 | 30 |
Si vous bloquez (ce qui est probable, ce problème n'est pas trivial), vous pouvez vous aider des quelques indications supplémentaires sous le programme.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52 | |
Indications supplémentaires
- Ligne 24 : il s'agit de copier par compréhension.
- Ligne 27 : on veut aller réellement jusqu'à la recherche d'une planche de valeur taille. Attention donc à la valeur finale...
- Ligne 30 : il s'agit de dire qu'au départ, on considère que le meilleur prix consiste à ne pas découper la planche. On prend donc le prix d'une telle planche entière.
- Ligne 36 : de la même façon, on prend juste le prix de cette découpe "entière", sans chercher à l'optimiser.
- Ligne 37 : on cherche le prix de vente optimum pour le reste de la planche après découpe. La taille étant plus petite, la planification des sous-problèmes nous permet d'affirmer qu'on dispose déja de cette sous-solution dans la mémoire-cache !
- Ligne 38 Classique sur les recherches de maximum. On se demande si le nouveau prix de vente est meilleur que l'ancien. On remplace le maximum au besoin.
- Ligne 43 Nous venons de terminer la recherche de la meilleure vente pour cette planche. Reste à mémoïser la valeur dans le cache m.
- Ligne 47 Il suffit de savoir où se trouve la réponse dans le cache m.
...CORRECTION...
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52 | |
16° Quelle est la meilleure découpe à faire pour des planches de 9 mètres ?
...CORRECTION...
Il suffit de lancer l'appel en fournissant 9 en argument et de regarder la valeur finale.
>>> meilleure_vente(LES_PRIX, 9)
Recherche pour une planche de 1m initialement à 1
Meilleur prix pour une planche de 1m : 1
Recherche pour une planche de 2m initialement à 5
1 + 1 rapporte 2
Meilleur prix pour une planche de 2m : 5
Recherche pour une planche de 3m initialement à 8
1 + 2 rapporte 6
2 + 1 rapporte 6
Meilleur prix pour une planche de 3m : 8
Recherche pour une planche de 4m initialement à 9
1 + 3 rapporte 9
2 + 2 rapporte 10
3 + 1 rapporte 9
Meilleur prix pour une planche de 4m : 10
Recherche pour une planche de 5m initialement à 10
1 + 4 rapporte 11
2 + 3 rapporte 13
3 + 2 rapporte 13
4 + 1 rapporte 10
Meilleur prix pour une planche de 5m : 13
Recherche pour une planche de 6m initialement à 17
1 + 5 rapporte 14
2 + 4 rapporte 15
3 + 3 rapporte 16
4 + 2 rapporte 14
5 + 1 rapporte 11
Meilleur prix pour une planche de 6m : 17
Recherche pour une planche de 7m initialement à 17
1 + 6 rapporte 18
2 + 5 rapporte 18
3 + 4 rapporte 18
4 + 3 rapporte 17
5 + 2 rapporte 15
6 + 1 rapporte 18
Meilleur prix pour une planche de 7m : 18
Recherche pour une planche de 8m initialement à 20
1 + 7 rapporte 19
2 + 6 rapporte 22
3 + 5 rapporte 21
4 + 4 rapporte 19
5 + 3 rapporte 18
6 + 2 rapporte 22
7 + 1 rapporte 18
Meilleur prix pour une planche de 8m : 22
Recherche pour une planche de 9m initialement à 24
1 + 8 rapporte 23
2 + 7 rapporte 23
3 + 6 rapporte 25
4 + 5 rapporte 22
5 + 4 rapporte 20
6 + 3 rapporte 25
7 + 2 rapporte 22
8 + 1 rapporte 21
Meilleur prix pour une planche de 9m : 25
25
Good Job. Un vrai bucheron !

4 - Mémoïsation sans trop de planification
Hors Programme
La mémoïsation directe des résultats n'est pas au programme de T-NSI. Mais c'est un prolongement naturelle de la programmation dynamique et cela peut faire un beau sujet pour l'épreuve du grand oral.
Comme vous venez de le voir, la programmation dynamique consiste à se demander comment traiter et mémoriser peu à peu les sous-problèmes.
Or, parfois, il n'est pas si facilement que cela de savoir dans quel sens travailler.
Sur certains problèmes, il est même possible que la façon de planifier les sous-problèmes dépends des données...
Dans ce cas, on peut utiliser simplement la mémoïsation sans l'aspect planification :
- On se crée une structure de données permettant de stocker les résultats
- Lorsqu'on veut résoudre un sous-problème
- Si la solution a déjà été trouvée et mémoïsée : on va juste lire la réponse dans la mémoire
- Si la solution n'existe pas encore : on la calcule puis on la mémoïse
Comme sur un bloc-note...
La programmation dynamique utilise souvent une approche impérative (à boucle de boucle), la mémoïsation directe utilise souvent plutôt une approche récursive.
Nous allons reprendre notre recheche d'incertitude dans la File d'attente avec notre suite de Fibonacci. On va rajouter un paramètre m possédant une valeur par défaut qui va contenir la mémoire qui va stocker au fur et à mesure les résultats obtenus.

f(n) = f(n - 1) + f(n - 2)
Les deux cas de base sont toujours f(0) = 0 et f(1) = 1.
17° Utiliser le programme ci-dessous pour répondre aux questions ci-dessous.
- A l'aide d'une traduction en Français des lignes 01 et 12 à 17, expliquer ce que va contenir le tableau-mémoire-cache m lors du premier appel.
- Expliquer ensuite le reste du fonctionnement (L19-L23).
- Conclure sur le nombre d'appels en réfléchissant sur le nombre de cas de base disponibles au fur et à mesure des calculs
L'exemple donné ligne 14 vous permettra de voir qu'on ne désire pas une traduction "mot à mot".
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 | |
18° Réaliser une version où le cache est un dictinnaire où les clés sont les n déjà calculés et les valeurs associées les réponses f(n).
...CORRECTION...
1
2
3
4
5
6
7
8
9
10
11
12
13
14 | |
Mémoïsation directe
Principe
La stratégie de la mémoïsation consiste à mémoriser temporairement en RAM les différents résultats intermédiaires pour ne jamais refaire deux fois la même chose.
Ce terme de mémoïsation a été introduit par Donald Michie en 1968 dans ces travaux de résolution des problèmes d’optimisation.
On parvient donc à réduire la complexité temporelle au détriment de la complexité en espace-mémoire : on utilise la ressource mémoire pour remplacer une partie de la ressource calcul du processeur.
1
2
3
4
5
6
7
8
9
10
11
12
13
14 | |
Mémoïsation plus longue
Plutôt que de tout recalculer, on peut aussi éventuellement placer la mémoire-cache en variable globale. De cette façon, tant que le programme est en marche, on garde trace de tous les calculs précédents.
1
2
3
4
5
6
7
8
9
10
11
12
13
14 | |
Deux défauts importants :
- Si on travaille avec des tableaux statiques, cela oblige en plus de choisir une taille maximale pour la mémoire-cache.
- A manier avec précaution si cette mémoire-cache peut prendre une taille arbitrairement grande (on travaille avec des tableaux dynamiques ou des dictionnaires) et donc saturer la RAM.
C'est pour cela qu'on utilise très rarement cette technique. Et il s'agit d'une variable globale, on a donc toujours les mises en garde habituelles à avoir en tête.
Mémorisation réelle ?
On pourrait se demander pourquoi mettre la mémoire des calculs précédents en RAM plutôt qu'en mémoire de masse dans un fichier pour ne pas avoir à refaire les calculs à chaque fois qu'on redémarre le processus.
La réponse est simple : à cause du temps d'accès à la mémoire de masse.
Finissons avec la version mémoïsée de la découpe d'arbres.
20° Répondre aux questions après avoir regardé la fonction meilleure_vente().
- Dans la mémoire-cache m, quelle valeur encode le fait qu'on n'ai pas encore déterminé la meilleure vente possible pour une longueur donnée ?
- Quels sont les deux seuls cas où on pourra définir un cas de base pour le moment ?
- Pourquoi n'a-t-on pas eu besoin de faire cela avec la programmation dynamique ? (nous avions juste initialisé m comme une simple copie de prix).
- meilleure_vente() est-elle une fonction récursive ?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53 | |
20° Finaliser la deuxième fonction (qui elle est récursive) pour que votre programme fonctionne correctement.
...CORRECTION...
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53 | |
Activité publiée le 22 03 2021
Dernière modification : 22 03 2021
Auteur : ows. h.