12 - k plus proches voisins
Nous allons voir aujourd'hui un premier algorithme prédictif qu'on peut classer dans la catégorie des algorithmes permettant de faire de l'intelligence artificielle.

On rappellera donc en introduction que IA veut dire Intelligence Artificielle en français. En réalité, il s'agit de la traduction de Artificial Intelligence. Or Intelligence en Anglais ne veut pas vraiment dire intelligence en Français !
Par exemple, Intelligence Service veut dire Service de Renseignements, les services secrets en gros.
Et c'est ainsi qu'il faut comprendre IA : c'est un ensemble de programmes qui ont pour but d'analyser un ensemble de données pour en tirer une conclusion. Il s'agit donc bien d'un travail d'analyse de données.
Logiciel nécessaire pour l'activité : Python 3 : Thonny, IDLE ou le site repl.it ...
Prérequis : les activités suivantes
- Python : Introduction à l'Opendata,
- Données : Utilisation d'une table de données et
- Données : Recherche dans une table de données.
Evaluation ✎ : questions 07-11-12-14-17-18-19-20
Documents de cours :
1 - Présentation
Nous allons travailler sur des données.
Elles ont été reconstituées à partir des données tirées de la coupe du monde 2018.
Le fichier complet se trouve ici mais nous n'allons utiliser qu'une version tronquée : celle ne contenant que les joueurs des 4 premières équipes, à savoir la France, la Croatie, la Belgique et l'Angleterre.
Nous voudrions voir s'il est possible d'associer un type de joueur (attaquant, milieu de terrain, défenseur ou gardien) en fonction de sa taille et de son poids. Pour cela, pas besoin de sortir Python dans premier temps : les tableurs comme celui d'OpenOffice peuvent ouvrir le fichier CSV et il ne reste qu'à créer des graphiques.
Voici le résultat :
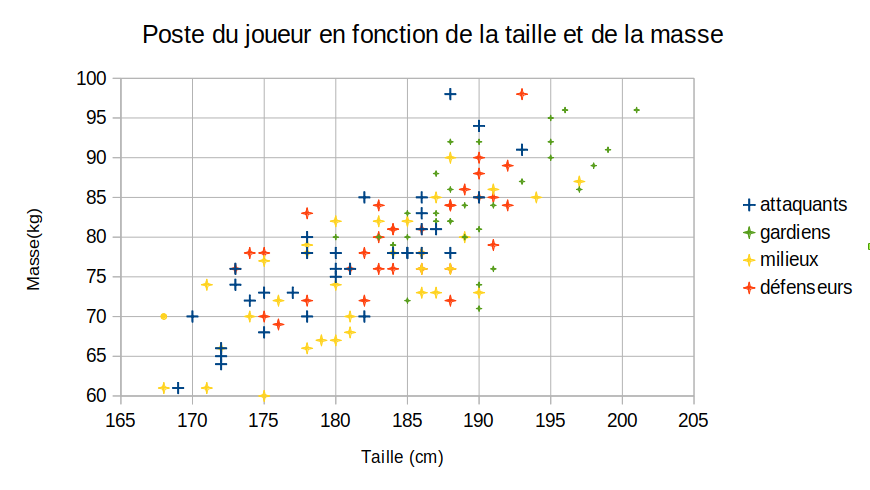
Bon... Pas de catégorie caractérisée par un type unique de carrure. Mais il y a bien quelques schémas visibles.
Et c'est maintenant que nous allons devoir sortir l'algorithmique : ce n'est pas intuitif mais il existe un moyen de prédire (ici approximativement, on reste sur de l'humain).
Imaginons que vous ayez un joueur à placer. Ici représenté par le point noir (70 kg, 180 cm):
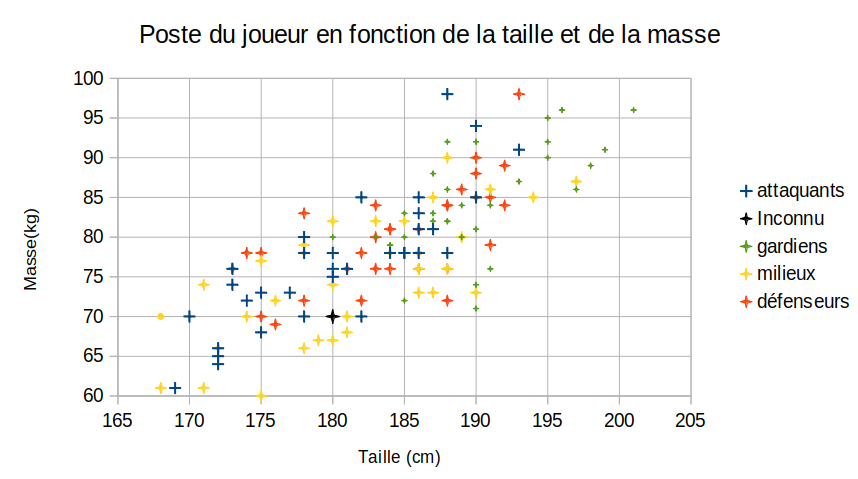
Alors, on lui donne quel rôle à celui là ?
Ici, c'est facile et cela va vous permettre de comprendre le principe de l'algorithme de k plus proches voisins.
Imaginons qu'on parte avec un algorithme des 9 plus proches voisins.
Voici le résultat graphique :
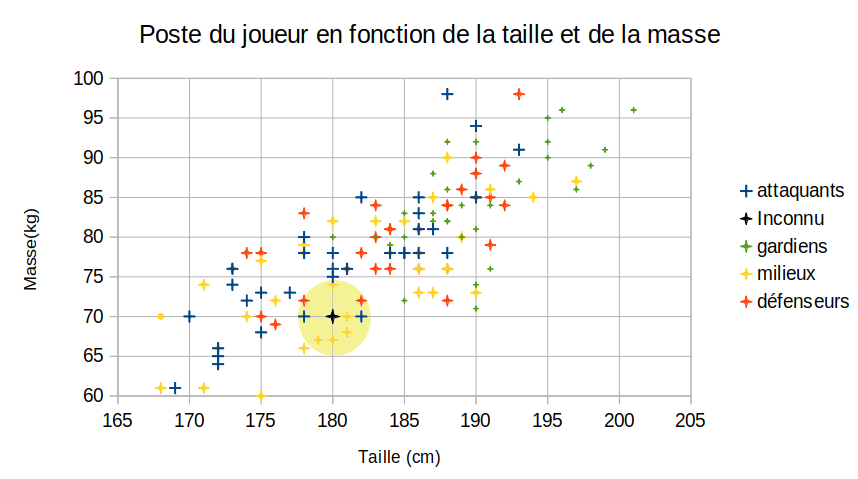
Si on compte, on obtient donc :
- 5 voisins milieux de terrain
- 2 voisins défenseurs
- 2 voisins attaquants
Nous aurions donc tendance à dire que notre joueur a plutôt un profil de milieu de terrain, non ?
Attention : j'ai pris ici un exemple avec une forte influence humaine. Il est clair que la masse et la taille ne permettent pas à coup sur de prévoir le poste d'un joueur. Il s'agit juste ici de prédire à quel poste un joueur sera le plus compétent en ne connaissant que ces deux caractéristiques physiques.
Il y a notamment un problème : deux joueurs avec la même masse et la même taille peuvent être à des postes différents. Il y a en effet des variables cachées (vitesse, accélération, précision ...) J'aurai pu prendre les caractéristiques qu'on trouve dans les jeux vidéos, mais est-ce bien caractéristique ?
Voici donc le principe de l'algorithme des k plus proches voisins : on regarde quelles sont les catégories des k enregistrements les plus proches de celui qu'on étudie et on pourra répondre. L'algorithme répond en fournissant la catégorie (ou les catégories en cas d'égalité) la plus représentée.
Attention néanmoins à la qualité de vos données : c'est là l'une des plus grandes difficultés des techniques d'intelligence artificielle : ne pas biaiser le résultat en fournissant des données incorrectes !
La première critique qu'on peut avoir sur notre jeu de données (les joueurs des 4 premières équipes) est qu'il n'y a pas le même nombre de joueurs dans chaque catégorie alors que les catégories ne sont pas clairement marquées par une zone. Du coup, celle qui apparaît le plus souvent à statistiquement un avantage certain.
Nous allons donc remédier à cela en rajoutant des joueurs dans les catégories les moins fournies.
Notre collection de base contient :
- 23 attaquants
- 33 défenseurs
- 12 gardiens
- 24 milieux de terrain
Il faudra donc monter à au moins une trentaine de joueurs par catégorie.
Du coup, j'ai récupéré également certains attaquants, gardiens de but et milieu de terrain dans les équipes suivantes dans le classement.
Ensuite, j'ai créé deux jeux de données de façon aléatoire :
- 75% des joueurs par catégorie pour créer le jeu d'apprentissage ou d’entraînement.
- Les 25% restants vont servir à créer le jeu de tests : nous allons tenter de comparer le poste réel des joueurs de ce jeu avec le poste que l'algorithme donne.
Voici les rendus graphiques de la nouvelle collection d'entraînement :
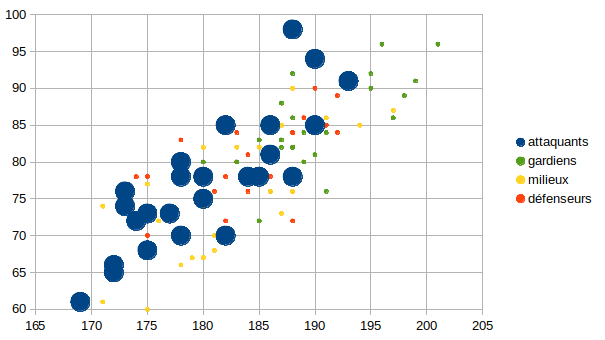
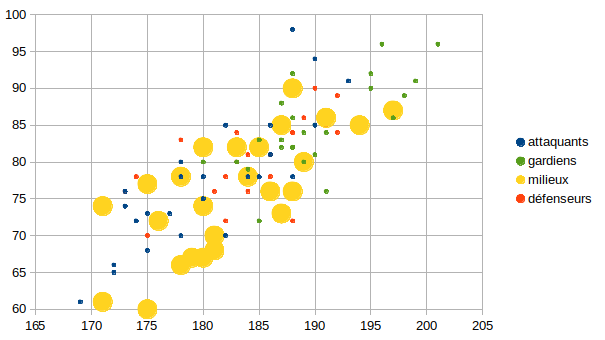
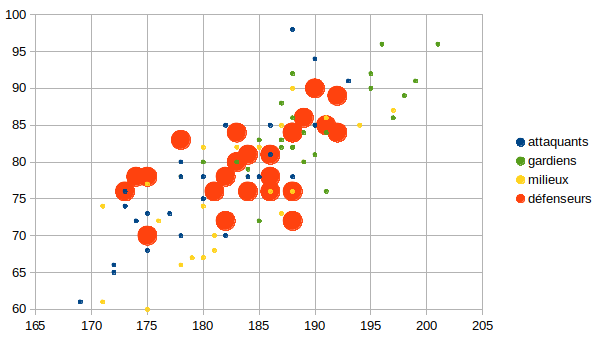
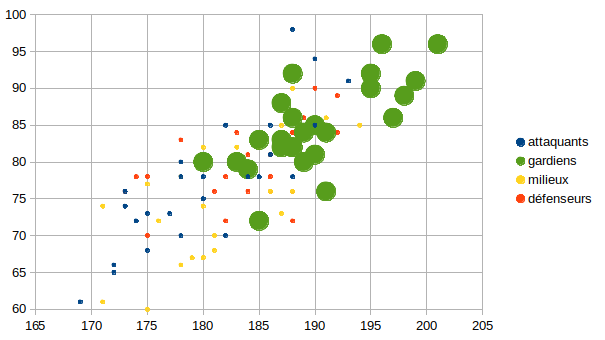
Le but est d'avoir une collection de données fiables qui donne à chaque enregistrement un descripteur ou attribut précis.
Notre collection est initialement stockée dans un fichier CSV.
A titre d'exemples, voici les trois premières lignes du fichier CSV que nous allons manipuler :
Poste,Taille (cm),Masse (kg)
Attaquant,178,80
Attaquant,184,7801° Créer un dossier knn sur votre ordinateur. Récupérer les fichiers suivants (clic-droit, enregister sous) en les plaçant dans votre dossier.
Optionnel : et si vous voulez les CSV plus complets (pour savoir qui est qui) :
Le fichier creation_collection.py est celui que nous avons utilisé lors de l'activité Données : Recherche dans une table de données, celle avec les Pokemons.
Pour rappel, il contient plusieurs fonctions :
decomposer(chaine, separateur): une fonction qui décompose la chaine et créant un tableau contenant les valeurscreer(entree, attributs): fonction qui renvoie un dictionnaire à partir de entree avec les clés fournies dans attributs.- et surtout
creer_collection(nom_fichier): Fonction qui renvoie un tableau de dictionnaire à partir d'un fichier CSV dont la première ligne contient les intitulés des en-têtes et les lignes suivantes les enregistrements.
>>> decomposer('1,voiture,sport,rouge', ',')
['1', 'voiture', 'sport', 'rouge']
>>> creer([0, 'voiture', 'sport', 'rouge'], ['id', 'type', 'utilisation', 'couleur'])
{'id': 0, 'type': 'voiture', 'utilisation': 'sport', 'couleur': 'rouge'}
02° Ouvrir l'un des fichiers CSV avec un éditeur de texte pour vérifier qu'il s'agit bien d'un simple fichier texte utilisant des virgules pour séparer les descripteurs / attributs.
Fermer le fichier.
03° Ouvrir l'un des fichiers CSV avec un tableur pour vérifier qu'il s'agit bien d'un moyen d'encoder un tableau de données.
Fermer le fichier.
Nous avons donc quelque chose qui ressemble à ceci :
| Collection / Table | Attributs ou Descripteurs | ||
| Poste | Taille (cm) | Masse (kg) | |
|---|---|---|---|
| Enregistrement d'index 0 | Attaquant | 178 | 80 |
| Enregistrement d'index 1 | Attaquant | 184 | 78 |
| ... | ... | ... | ... |
04° Créer maintenant un fichier gestion.py situé dans le dossier knn et contenant ceci :
1
2 | from creation_collection import creer_collection
joueurs = creer_collection("entrainement.csv")
|
📁 knn
📄 gestion.py
📄 creation_collection.py
📄 entrainement.csv
📄 test.csv
05° Lancer le programme. Vous devriez parvenir à utiliser la fonction creer_collection dont le code se trouve dans le fichier python nommé creation_collection.py.
En tout cas, ça devrait marcher si les deux fichiers sont bien au même endroit.
06° Tapez ceci dans la console pour voir le contenu de la variable joueurs.
>>> joueurs
[{'Poste': 'Attaquant', 'Taille (cm)': '178', 'Masse (kg)': '80'}, {'Poste': 'Attaquant', 'Taille (cm)': '184', 'Masse (kg)': '78'}, {'Poste': 'Attaquant', 'Taille (cm)': '188', 'Masse (kg)': '98'}, {'Poste': 'Attaquant', 'Taille (cm)': '180', 'Masse (kg)': '78'}, {'Poste': 'Attaquant', 'Taille (cm)': '169', 'Masse (kg)': '61'}, {'Poste': 'Attaquant', 'Taille (cm)': '173', 'Masse (kg)': '74'}, {'Poste': 'Attaquant', 'Taille (cm)': '190', 'Masse (kg)': '94'}, {'Poste': 'Attaquant', 'Taille (cm)': '180', 'Masse (kg)': '75'}, {'Poste': 'Attaquant', 'Taille (cm)': '182', 'Masse (kg)': '70'}, {'Poste': 'Attaquant', 'Taille (cm)': '175', 'Masse (kg)': '68'}, {'Poste': 'Attaquant', 'Taille (cm)': '175', 'Masse (kg)': '73'}, {'Poste': 'Attaquant', 'Taille (cm)': '190', 'Masse (kg)': '85'}, {'Poste': 'Attaquant', 'Taille (cm)': '186', 'Masse (kg)': '81'}, {'Poste': 'Attaquant', 'Taille (cm)': '177', 'Masse (kg)': '73'}, {'Poste': 'Attaquant', 'Taille (cm)': '185', 'Masse (kg)': '78'}, {'Poste': 'Attaquant', 'Taille (cm)': '193', 'Masse (kg)': '91'}, {'Poste': 'Attaquant', 'Taille (cm)': '174', 'Masse (kg)': '72'}, {'Poste': 'Attaquant', 'Taille (cm)': '173', 'Masse (kg)': '76'}, {'Poste': 'Attaquant', 'Taille (cm)': '172', 'Masse (kg)': '65'}, {'Poste': 'Attaquant', 'Taille (cm)': '178', 'Masse (kg)': '70'}, {'Poste': 'Attaquant', 'Taille (cm)': '178', 'Masse (kg)': '78'}, {'Poste': 'Attaquant', 'Taille (cm)': '188', 'Masse (kg)': '78'}, {'Poste': 'Attaquant', 'Taille (cm)': '182', 'Masse (kg)': '85'}, {'Poste': 'Attaquant', 'Taille (cm)': '172', 'Masse (kg)': '66'}, {'Poste': 'Attaquant', 'Taille (cm)': '186', 'Masse (kg)': '85'}, {'Poste': 'Défenseur', 'Taille (cm)': '175', 'Masse (kg)': '78'}, {'Poste': 'Défenseur', 'Taille (cm)': '191', 'Masse (kg)': '85'}, {'Poste': 'Défenseur', 'Taille (cm)': '174', 'Masse (kg)': '78'}, {'Poste': 'Défenseur', 'Taille (cm)': '173', 'Masse (kg)': '76'}, {'Poste': 'Défenseur', 'Taille (cm)': '178', 'Masse (kg)': '83'}, {'Poste': 'Défenseur', 'Taille (cm)': '182', 'Masse (kg)': '72'}, {'Poste': 'Défenseur', 'Taille (cm)': '188', 'Masse (kg)': '72'}, {'Poste': 'Défenseur', 'Taille (cm)': '175', 'Masse (kg)': '70'}, {'Poste': 'Défenseur', 'Taille (cm)': '183', 'Masse (kg)': '80'}, {'Poste': 'Défenseur', 'Taille (cm)': '189', 'Masse (kg)': '86'}, {'Poste': 'Défenseur', 'Taille (cm)': '186', 'Masse (kg)': '81'}, {'Poste': 'Défenseur', 'Taille (cm)': '188', 'Masse (kg)': '84'}, {'Poste': 'Défenseur', 'Taille (cm)': '188', 'Masse (kg)': '76'}, {'Poste': 'Défenseur', 'Taille (cm)': '192', 'Masse (kg)': '84'}, {'Poste': 'Défenseur', 'Taille (cm)': '186', 'Masse (kg)': '78'}, {'Poste': 'Défenseur', 'Taille (cm)': '184', 'Masse (kg)': '76'}, {'Poste': 'Défenseur', 'Taille (cm)': '188', 'Masse (kg)': '84'}, {'Poste': 'Défenseur', 'Taille (cm)': '181', 'Masse (kg)': '76'}, {'Poste': 'Défenseur', 'Taille (cm)': '192', 'Masse (kg)': '89'}, {'Poste': 'Défenseur', 'Taille (cm)': '190', 'Masse (kg)': '90'}, {'Poste': 'Défenseur', 'Taille (cm)': '184', 'Masse (kg)': '81'}, {'Poste': 'Défenseur', 'Taille (cm)': '183', 'Masse (kg)': '84'}, {'Poste': 'Défenseur', 'Taille (cm)': '183', 'Masse (kg)': '84'}, {'Poste': 'Défenseur', 'Taille (cm)': '182', 'Masse (kg)': '78'}, {'Poste': 'Défenseur', 'Taille (cm)': '186', 'Masse (kg)': '76'}, {'Poste': 'Gardien', 'Taille (cm)': '191', 'Masse (kg)': '76'}, {'Poste': 'Gardien', 'Taille (cm)': '196', 'Masse (kg)': '96'}, {'Poste': 'Gardien', 'Taille (cm)': '185', 'Masse (kg)': '72'}, {'Poste': 'Gardien', 'Taille (cm)': '197', 'Masse (kg)': '86'}, {'Poste': 'Gardien', 'Taille (cm)': '199', 'Masse (kg)': '91'}, {'Poste': 'Gardien', 'Taille (cm)': '195', 'Masse (kg)': '92'}, {'Poste': 'Gardien', 'Taille (cm)': '188', 'Masse (kg)': '86'}, {'Poste': 'Gardien', 'Taille (cm)': '180', 'Masse (kg)': '80'}, {'Poste': 'Gardien', 'Taille (cm)': '183', 'Masse (kg)': '80'}, {'Poste': 'Gardien', 'Taille (cm)': '191', 'Masse (kg)': '84'}, {'Poste': 'Gardien', 'Taille (cm)': '201', 'Masse (kg)': '96'}, {'Poste': 'Gardien', 'Taille (cm)': '188', 'Masse (kg)': '82'}, {'Poste': 'Gardien', 'Taille (cm)': '195', 'Masse (kg)': '90'}, {'Poste': 'Gardien', 'Taille (cm)': '190', 'Masse (kg)': '85'}, {'Poste': 'Gardien', 'Taille (cm)': '188', 'Masse (kg)': '92'}, {'Poste': 'Gardien', 'Taille (cm)': '189', 'Masse (kg)': '84'}, {'Poste': 'Gardien', 'Taille (cm)': '187', 'Masse (kg)': '88'}, {'Poste': 'Gardien', 'Taille (cm)': '188', 'Masse (kg)': '82'}, {'Poste': 'Gardien', 'Taille (cm)': '190', 'Masse (kg)': '81'}, {'Poste': 'Gardien', 'Taille (cm)': '185', 'Masse (kg)': '83'}, {'Poste': 'Gardien', 'Taille (cm)': '189', 'Masse (kg)': '80'}, {'Poste': 'Gardien', 'Taille (cm)': '187', 'Masse (kg)': '83'}, {'Poste': 'Gardien', 'Taille (cm)': '198', 'Masse (kg)': '89'}, {'Poste': 'Gardien', 'Taille (cm)': '187', 'Masse (kg)': '82'}, {'Poste': 'Gardien', 'Taille (cm)': '184', 'Masse (kg)': '79'}, {'Poste': 'Milieu de terrain', 'Taille (cm)': '183', 'Masse (kg)': '82'}, {'Poste': 'Milieu de terr…
✎ 07° La collection est-elle ici un tableau de tableaux, un tableau de tuples ou un tableau de dictionnaires ?
Que va-t-on obtenir si on tape ceci dans la console ?
Les valeurs associées aux différentes clés sont-elles uniquement des strings ou parfois des integers (regardez bien l'écran, ne donnez pas votre avis !) ?
>>> joueurs[1]
Nous allons maintenant voir comment parvenir à créer quatre représentations de nos données sur un même graphique.
Nous allons utiliser la bibliothèque matplotlib. Si elle n'est pas installé, il va falloir l'installer dans Thonny (Tools-Manage Packages) ou directement avec pip si vous travaillez avec IDLE (tapez alors ceci dans un terminal système : python -m pip install --user matplotlib ).
08° Utiliser le nouveau programme gestion.py suivant.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34 | from creation_collection import creer_collection
from matplotlib import pyplot as plt
# Collection : Création de la collection
joueurs = creer_collection("entrainement.csv")
# Collection : transformation en entiers des descripteurs numériques
for index in range(len(joueurs)):
joueurs[index]['Taille (cm)'] = int(joueurs[index]['Taille (cm)'])
joueurs[index]['Masse (kg)'] = int(joueurs[index]['Masse (kg)'])
# Graphiques : Création des listes X Y par extension et ajouts successifs
xA = []
yA = []
xD = []
yD = []
for joueur in joueurs:
if joueur['Poste'] == 'Attaquant':
xA.append(joueur['Taille (cm)'])
yA.append(joueur['Masse (kg)'])
elif joueur['Poste'] == 'Défenseur':
xD.append(joueur['Taille (cm)'])
yD.append(joueur['Masse (kg)'])
# Graphiques : affichage des données
plt.plot(xA,yA, 'b+', label="Attaquants")
plt.plot(xD,yD, 'rx', label="Défenseurs")
plt.grid()
plt.xlabel("Taille (cm)")
plt.ylabel("Masse (kg)")
plt.title("Les différents types de joueurs")
plt.legend(loc='upper left')
plt.show()
|
Vous devriez avoir un graphique de ce type sous les yeux.
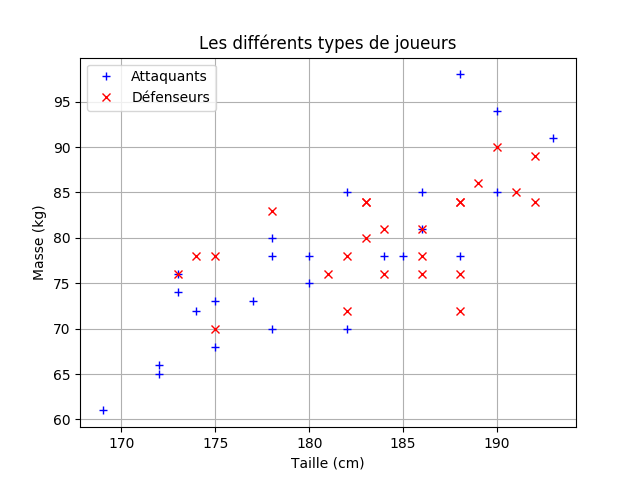
On voit clairement que la classification pure des joueurs en fonction de la taille et du poids n'est pas possible
09° Que fait-on sur les lignes 8, 9 et 10 ?
...CORRECTION...
Il s'agit de lire et modifier éventuellement les enregistrements un par un dans le tableau.
On utilise un index car nous allons devoir modifier les enregistrements.
On transforme les valeurs associées aux clés en entiers car nous avons créé nos enregistrements à partir d'un fichier CSV et toutes les valeurs sont donc par défaut des strings.
10° Après avoir lu les lignes 18 à 24, répondre aux QMC suivants :
Les tableaux x et y sont créés
- A : Par compréhension
- B : Par intrusion
- C : Par extension
- D : Par confusion
Que contient le tableau xA ?
- A : Les tailles des défenseurs
- B : Les tailles des attaquants
- C : Les poids des défenseurs
- D : Les poids des attaquants
...CORRECTION...
On utilise la méthode append : il s'agit donc d'une construction par extension par ajouts successifs.
18
19
20 | for joueur in joueurs:
if joueur['Poste'] == 'Attaquant':
xA.append(joueur['Taille (cm)'])
|
Pour la deuxième question, on voit donc qu'on rajoute à xA les valeurs associées à la clé 'Taille (cm)' uniquement si l'enregistrement possède un descripteur 'Poste' contenant 'Attaquant'.
Nous aurions pu utiliser également la méthode par compréhension :
1
2
3
4 | xA = [joueur['Taille (cm)'] for joueur in joueurs if joueur['Poste'] == 'Attaquant']
yA = [joueur['Masse (kg)'] for joueur in joueurs if joueur['Poste'] == 'Attaquant']
xD = [joueur['Taille (cm)'] for joueur in joueurs if joueur['Poste'] == 'Défenseur']
yD = [joueur['Masse (kg)'] for joueur in joueurs if joueur['Poste'] == 'Défenseur']
|
Mais cela veut dire qu'il faut lire un à un les enregistrements par chaque création. Si on a 4 millions d'enregistrements, cela veut dire ici lire 16 millions d'enregistrements.
✎ 11° Modifier le programme pour pouvoir afficher également les milieux de terrain et les gardiens.
Vous utilisez ces codes pour afficher les joueurs (le orange n'existe pas en version déclaration simplifiée, d'où un ensemble de paramètres un peu différent pour la représentation des milieux de terrain) :
1
2 | plt.plot(xM,yM, color='orange', marker='+',linewidth=0, label="Milieux de terrain")
plt.plot(xG,yG, 'gx', label="Gardiens de but")
|
Après modification du programme, vous devriez avoir quelque chose de proche de cela :
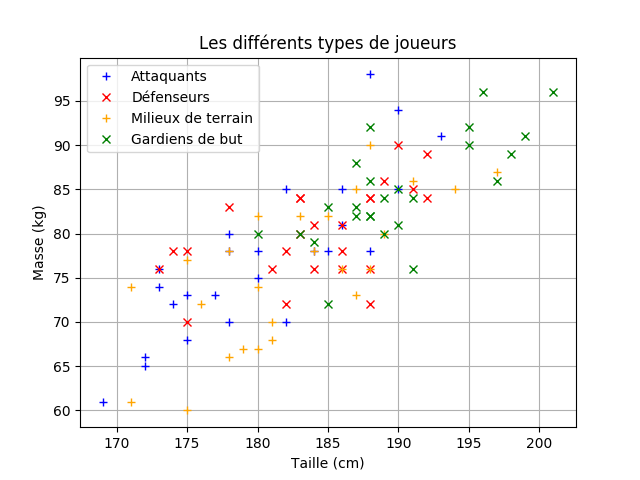
Voilà : nous sommes parvenus à transformer notre fichier CSV en collection Python et à représenter celle-ci sur un graphique.
Il nous reste à appliquer l'algorithme des k plus proches voisins ou knn. Et pourquoi knn ?
Cela veut dire k-nearest neighbors algorithm.
2 - Algorithme knn
Commençons par voir le principe de cet algorithme.
Il est possible mais compliqué d'écrire cet algorithme sans avoir accès aux dictionnaires. Nous considérons ici que ce type de structure de données est disponible.
Nous allons l'étudier en détail une version Python dans la partie suivante. Il s'agit ici de fournir le principe de travail hors d'un contexte de programmation.
✎ 12° Lire la description de l'algorithme suivant. Expliquer son fonctionnement en écrivant une phrase simple décrivant chacune des étapes qui y sont décrites. Le but est ici d'expliquer le fonctionnement global par des phrases un peu plus fournies que mes commentaires mais moins compliquées que l'algorithme.
Algorithme des k plus proches voisins
But : trouver la catégorie la plus présente parmi les k plus proches enregistrements voisins d'un enregistrement dont on voudrait estimer la catégorie.
Principe basique :
- on calcule les distances entre l'enregistrement de catégorie inconnue et les enregistrements de notre collection. On range les couples (distance, catégorie de l'enregistrement) dans un tableau memoire.
- On trie le tableau memoire en fonction de la distance
- On ne retient que les k plus petites distances
- On répond en fournissant la catégorie (ou les catégories éventuellement) la plus présente
Description des entrées / sortie
ENTREES:k: un entier correspondant aux nombres de proches voisins à gérernouveau: un enregistrement dont on cherche à déterminer la catégorie.collection: un tableau contenant un ensemble d'enregistrements contenant plusieurs descripteurs dont une catégorie d'appartenance. On considère qu'il possède au moins k éléments.- (optionnelle selon les langages d'implémentation):
longueur, le nombre d'éléments danscollection SORTIE: la ou les catégories possibles.
Algorithme commenté
Dans l'algorithme ci-dessous
la fonction distance désigne une fonction renvoyant un nombre caractérisant l'éloignement de deux enregistrements.
la fonction cleMajoritaire renvoie la catégorie la plus représentée dans un dictionnaire.
la fonction tri permet de trier le tableau.
⚐ Etape 1 ➡ ajout de k couples (distance, catégorie) dans memoire
memoire ← Tableau vide ayant longueur éléments
index ← 0
TANT QUE index < k
d ← distance (nouveau, collection[index])
on calcule la distance entre les deux enregistrements
categorie ← collection[index]['Poste']
on récupère la catégorie de l'enregistrement via la clé 'Poste'
memoire[index] ← (d, categorie)
on mémorise un couple (p-uplet) contenant distance et catégorie
index ← index + 1
on avance dans la lecture de la collection
Fin du TANT QUE
trie(memoire) en ordre croissant de distance (l'index 0)
laPlusGrande ← memoire[k-1][0]
⚐ Etape 2 ➡ on lit la suite mais on ne mémorise que si la distance est plus petite que l'une des précédentes
TANT QUE index < longueur de la collection
d ← distance (nouveau, collection[index])
On calcule la distance entre les deux enregistrements
SI d < laPlusGrande en mémoire
categorie ← collection[index]['Poste']
On récupère la catégorie de l'enregistrement
memoire[k-1] ← (d, categorie)
On place le couple (distance,catégorie) en mémoire en dernière position
trie(memoire) en ordre croissant de distance (l'index 0)
laPlusGrande ← memoire[k-1][0]
Fin du SI
index ← index + 1
Fin du TANT QUE
⚐ Etape 3 ➡ on compte les catégories présentes
nombres ← Dictionnaire vide
index ← 0
TANT QUE index < k
categorie ← memoire[index][1]
SI la clé categorie existe déjà dans le dictionnaire nombres
nombres[categorie] ← nombres[categorie] + 1
SINON
nombres[categorie] ← 1
Fin du SI
Fin TANT QUE
⚐ Etape 4 : on renvoie la catégorie majoritaire
reponse ← cleMajoritaire(nombres)
Renvoyer reponse
Algorithme non commenté
⚐ Etape 1
memoire ← Tableau vide ayant longueur éléments
index ← 0
TANT QUE index < k
d ← distance (nouveau, collection[index])
categorie ← collection[index]['Poste']
memoire[index] ← [d, categorie]
index ← index + 1
Fin du TANT QUE
trie(memoire) en ordre croissant de distance (l'index 0)
laPlusGrande ← memoire[k-1][0]
⚐ Etape 2
TANT QUE index < longueur de la collection
d ← distance (nouveau, collection[index])
SI d < laPlusGrande en mémoire
categorie ← collection[index]['Poste']
memoire[k-1] ← [d, categorie]
trie(memoire) en ordre croissant de distance (l'index 0)
laPlusGrande ← memoire[k-1][0]
Fin du SI
index ← index + 1
Fin du TANT QUE
⚐ Etape 3
nombres ← Dictionnaire vide
index ← 0
TANT QUE index < k
categorie ← memoire[index][1]
SI la clé categorie existe déjà dans le dictionnaire nombres
nombres[categorie] ← nombres[categorie] + 1
SINON
nombres[categorie] ← 1
Fin du SI
Fin TANT QUE
⚐ Etape 4
reponse ← cleMajoritaire(nombres)
Renvoyer reponse
On notera que j'élude ici le cas où plusieurs catégories apparaissent en même nombre. Nous verrons comment traiter ce cas avec Python.
3 - Recherche de la distance
Regardons chaque étape une par une.
Nous allons commencer par déterminer la distance entre deux enregistrements avec une fonction distance.
Comment ça fonctionne ? Tout simplement en calculant la distance entre les deux points dans le plan (xy).
Il existe plusieurs façons de calculer les distances.
Ici, j'ai juste pris la distance euclidienne que vous connaissez (en vert sur le dessin ci-dessous).

Distance euclidienne entre deux points
On considère deux points M1 et M2 dans un plan.
Les coordonnées de M1 sont (x1, y1).
Les coordonnées de M2 sont (x2, y2).
La distance euclidienne correspond à la valeur obtenue en réalisant le calcul suivant :
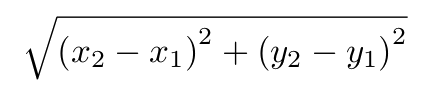
13° Calculer "à la main" la distance entre ces deux athlètes :
Joueur 1 : Masse 80kg, Taille 180 cm.
Joueur 2 : Masse 70kg, Taille 175 cm.
...CORRECTION...
Il faut faire le calcul suivant :
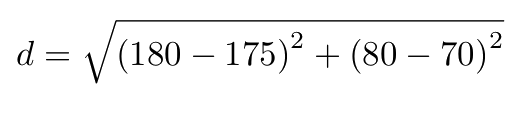
Avec Python, ça donne un calcul du type math.sqrt((180-175)**2+(80-70)**2)
On obtient donc une distance de 11.18 kg.cm
✎ 14° Calculer "à la main" la distance entre ces deux athlètes :
Joueur 1 : Masse 75kg, Taille 180 cm.
Joueur 2 : Masse 70kg, Taille 170 cm.
Voici le programme Python que nous allons utiliser pour calculer cette distance :
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31 | # 1 - Importation
from creation_collection import creer_collection
from matplotlib import pyplot as plt
from math import sqrt
from operator import itemgetter
# 2 - Déclaration des fonctions
def distance(enr1, enr2):
"""Fonction qui renvoie la distance entre les deux enregistrements"""
x1 = enr1['Taille (cm)']
x2 = enr2['Taille (cm)']
y1 = enr1['Masse (kg)']
y2 = enr2['Masse (kg)']
d = sqrt( (x2-x1)**2 + (y2-y1)**2 )
return d
# 3 - Programme
if __name__ == '__main__':
# Collection : Création de la collection
joueurs = creer_collection("entrainement.csv")
# Collection : transformation en entiers des descripteurs numériques
for index in range(len(joueurs)):
joueurs[index]['Taille (cm)'] = int(joueurs[index]['Taille (cm)'])
joueurs[index]['Masse (kg)'] = int(joueurs[index]['Masse (kg)'])
enr_test = {'Poste':'X', 'Taille (cm)':182, 'Masse (kg)':75}
|
15° Remplacer le programme gestion.py par celui-ci.
Lancer le nouveau programme.
Lancer les instructions suivantes dans la console de façon à calculer la distance entre notre enregistrement de catégorie inconnue enr_test et les deux premiers enregistrements de la collection.
Plus c'est petit, plus les deux enregistrements sont proches dans le plan (poids,taille).
>>> distance(enr_test, joueurs[0])
6.4031242374328485
>>> distance(enr_test, joueurs[1])
3.605551275463989
4 - Automatisation
Dans la prochaine activité, nous verrons comment automatiser l'algorithme avec Python.
En attendant, nous allons juste utiliser un programme tout fait qui réalise les deux premières étapes, à savoir :
- Etape 1 : calculer les distances sur les k premiers enregistrements
- Etape 2 : calculer la distance sur chacun des enregistrements suivants mais ne le placer en mémoire que si cette distance est plus petite que les précédentes.
Voici le contenu du programme gestion.py qui vous allez maintenant utiliser. Son étude se fera dans l'activité suivante. Aujourd'hui, vous n'aurez qu'à l'utiliser.
Il contient :
- La fonction distance qui estime la distance entre deux enregistrements contenant au moins la masse et la taille du joueur.
- La fonction knn qui réalise les étapes 1 et 2. On doit lui fournir les paramètres suivants : k, l'enregistrement nouveau à analyser et la collection des enregistrements connus.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67 | # 1 - Importation
from creation_collection import creer_collection
from matplotlib import pyplot as plt
from math import sqrt
from operator import itemgetter
# 2 - Déclaration des fonctions
def distance(enr1, enr2):
"""Fonction qui renvoie la distance entre les deux enregistrements
:: param enr1 (dict) :: un dictionnaire correspondant à un enregistrement
:: param enr2 (dict) :: un dictionnaire correspondant à un enregistrement
:: return (float) :: la distance euclidienne entre les deux enregistrements
"""
x1 = enr1['Taille (cm)']
x2 = enr2['Taille (cm)']
y1 = enr1['Masse (kg)']
y2 = enr2['Masse (kg)']
d = sqrt( (x2-x1)**2 + (y2-y1)**2 )
return d
def knn(k, nouveau, collection):
"""Fonction qui renvoie la catégorie supposée de nouveau
:: param k(int) :: le nombre de plus proches voisins à gérer
:: param nouveau(dict) :: un enregistrement sans connaissance de la clé de catégorie
:: param collection(list) :: une collection d'enregistrements
:: return (list) :: un tableau contenant la ou les catégories majoritaires
"""
# Etape 1 - ajout de k couples (distance, catégorie) dans memoire
memoire = []
for index in range(k):
d = distance(nouveau, collection[index])
categorie = collection[index]['Poste']
memoire.append( (d,categorie) )
memoire.sort(key=itemgetter(0))
laPlusGrande = memoire[k-1][0]
# Etape 2 - on rajoute les autres au cas par cas
for index in range(k, len(collection)):
d = distance(nouveau, collection[index])
if d < laPlusGrande:
categorie = collection[index]['Poste']
memoire[k-1] = (d,categorie)
memoire.sort(key=itemgetter(0))
laPlusGrande = memoire[k-1][0]
return memoire
# 3 - Programme
if __name__ == '__main__':
# Collection : Création de la collection
joueurs = creer_collection("entrainement.csv")
# Collection : transformation en entiers des descripteurs numériques
for index in range(len(joueurs)):
joueurs[index]['Taille (cm)'] = int(joueurs[index]['Taille (cm)'])
joueurs[index]['Masse (kg)'] = int(joueurs[index]['Masse (kg)'])
enr_test = {'Poste':'X', 'Taille (cm)':182, 'Masse (kg)':75}
|
16° Utiliser le programme gestion.py précédent pour placer les fonctions et les variables en mémoire.
Taper les instructions suivantes pour vérifier qu'il répond bien :
>>> joueurs[0]
{'Poste': 'Attaquant', 'Taille (cm)': 178, 'Masse (kg)': 80}
Cela permet de vérifier que les enregistrements contenus dans notre collection-tableau joueurs sont des dictionnaires.
>>> knn(3, enr_test, joueurs)
[
(1.4142135623730951, 'Défenseur'),
(2.0, 'Attaquant'),
(2.23606797749979, 'Défenseur')
]
Cette fois, nous constatons que les enregistrements contenus dans la collection-tableau memoire sont eux des p-uplets (distance, catégorie).
✎ 17° A vous de jouer : placer dans le programme la taille et la masse de quelqu'un que vous connaissez (ça peut être vous !). La modification se fait sur la ligne 67.
1 - Noter ces valeurs sur la copie numérique.
2 - Lancer le programme avec fournir les réponses pour k = 1.
A quel poste pourrait-on placer la personne ?
✎ 18° Donner maintenant la réponse de la fonction pour k = 3.
Expliquer alors le poste qu'on devrait attribuer.
✎ 19° Idem pour k = 7.
✎ 20° Idem pour k = 11.
5 - FAQ
Peut-on créer des graphiques sans créer de liste ?
Oui. Ici, il ne s'agit que de placer des points. Techniquement, il ne s'agit donc pas de courbes et donc nous aurions pu simplement placer des points.
Utiliser les listes me permet simplement de faire des révisions sur leurs créations par compréhension et par extension.
Voici une façon alternative (sans liste et donc plus simple) de créer le graphique avec les différents joueurs. Par contre, on notera qu'on ne peut pas juste demander d'afficher les labels : chaque point compte pour un label, il y en aura donc beaucoup. Si vous voulez voir le résultat, vous pouvez enlever le # de la ligne 30.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31 | from creation_collection import creer_collection
from matplotlib import pyplot as plt
# Collection : Création de la collection
joueurs = creer_collection("entrainement.csv")
# Collection : transformation en entiers des descripteurs numériques
for index in range(len(joueurs)):
joueurs[index]['Taille (cm)'] = int(joueurs[index]['Taille (cm)'])
joueurs[index]['Masse (kg)'] = int(joueurs[index]['Masse (kg)'])
# Graphique
for joueur in joueurs:
taille = joueur['Taille (cm)']
masse =joueur['Masse (kg)']
if joueur['Poste'] == 'Attaquant':
plt.plot(taille, masse, 'b+', label="Attaquants")
elif joueur['Poste'] == 'Défenseur':
plt.plot(taille, masse, 'rx', label="Défenseurs")
elif joueur['Poste'] == 'Gardien':
plt.plot(taille, masse, color='orange', marker='+',linewidth=0, label="Milieux de terrain")
elif joueur['Poste'] == 'Milieu de terrain':
plt.plot(taille, masse, 'gx', label="Gardiens de but")
plt.grid()
plt.xlabel("Taille (cm)")
plt.ylabel("Masse (kg)")
plt.title("Les différents types de joueurs")
#plt.legend(loc='upper left')
plt.show()
|
Activité publiée le 09 04 2020
Dernière modification : 02 04 2023
Auteur : ows. h.