11 - Preuve du tri par insertion

⏪

⏬

⏩

1 - Rappel

2 - Terminaison

3 - Coût

4 - Correction

5 - Python

6 - FAQ

Une activité-leçon assez théorique et mathématique par certains côtés. Mais vous allez voir aujourd'hui une chose assez fabuleuse : on peut prouver qu'un algorithme répond toujours correctement, ou pas...

Quasiment toutes les questions sont munies de la correction.

Logiciel nécessaire pour l'activité : Python 3 : Thonny, IDLE ou le site repl.it ...

Prérequis : Algorithme : tri par insertion

Evaluation ✎ : questions 13-14-18

Résumé de cours : open document ou pdf

MODE COURS (cacher les questions)

1 - Rappel visuel du tri et algorithme

⇩ ⇧ ⤊

Nous avons tout vu dans l'activité précédente. Si vous ne vous en souvenez plus trop, voici l'animation suivi de l'algorithme. Le tout est également disponible dans l'onglet FICHES de l'accueil de la partie ALGO.


Indice	00	01	02	03	04	05	06	07	08	09	10	11	12	13	14	15	16	17	18	19
Elément	90	60	20	50	80	10	90	99	30	90	70	10	20	70	98	30	40	90	90	60

Algorithme de tri par insertion

But : trier sur place un tableau initialement non trié.

(ici par odre croissant)

Description des entrées / sortie

ENTREES :

t : un tableau contenant au moins deux éléments.
(optionnelle selon les langages d'implémentation): longueur, le nombre d'éléments dans le tableau

SORTIE : aucune. Le t est trié sur place : on modifie directement t.

Exemple :

Prenons t = [13, 18, 89, 1024, 45, -12, 18]

Initialement le tableau contient donc cela :

Indice	0	1	2	3	4	5	6
Elément	13	18	89	1024	45	-12	18

Après le tri, le tableau contiendra cela :

Indice	0	1	2	3	4	5	6
Elément	-12	13	18	18	45	89	1024

Algorithme de tri par insertion, commenté

i est l'indice (flèche en vert clair dans l'animation) de la clé-valeur qu'il faut placer

POUR i variant de 1 à (longueur - 1) inclus

cle ← t[i]

on mémorise dans cle la valeur-clé car cette case risque d'être écrasée

j ← i - 1

La variable j contient initialement l'indice juste à gauche de la clé (flèche verte dans l'animation)

TANT QUE j ≥ 0 et que t[j] > cle

t[j+1] ← t[j]

On décale la valeur d'une case à droite

j ← j - 1

On passe à la case suivante à gauche

Fin TANT QUE

t[j+1] ← cle

On place la valeur-clé à la place voulue pour obtenir un sous-tableau trié

Fin POUR

Renvoyer VIDE (∅)

Algorithme de tri par insertion, non commenté

POUR i variant de 1 à (longueur - 1) inclus

cle ← t[i]

j ← i - 1

TANT QUE j ≥ 0 et que t[j] > cle

t[j+1] ← t[j]

j ← j - 1

Fin TANT QUE

t[j+1] ← cle

Fin POUR

Renvoyer VIDE (∅)

2 - Preuve de terminaison

⇩ ⇧ ⤊

Rappel : Preuve de terminaison

La preuve de terminaison d'un algorithme permet d'affirmer qu'il s'arrête de façon certaine sur toutes les entrées valides qu'on lui fournit (c'est à dire les entrées respectant les préconditions).

Preuve de terminaison : si les deux propositions suivantes sont vraies alors la boucle s'arrête :

Proposition A : les boucles s'expriment sous la forme TANT QUE VARIANT > 0
Proposition B : le VARIANT est une suite d'ENTIERS strictement décroissante.

(A et B) implique alors que l'algorithme se termine.

Attention à la négation

(A et B) implique que l'algorithme s'arrête TOUJOURS.

NON (A et B) ou encore (NON A) ou (NON B) d'après De Morgan n'implique rien de particulier.
Il est possible que l'algorithme ne boucle jamais, boucle parfois ou boucle toujours.

01° Je vous donne ci-dessous trois façons de faire la même chose. Analysez bien les trois façons de faire pour vous persuader que ces actions provoquent le même comportement de boucle.

Montrer alors la terminaison de la boucle en utilisant la version TANT QUE.

Version avec une boucle bornée POUR

POUR i variant de 45 à 199 inclus, par incrémentation de 10

Faire un truc (qui ne modifie pas la valeur de i !)

Fin POUR

Version avec une boucle non bornée TANT QUE

i ← 45

TANT QUE i < 200

Faire un truc (qui ne modifie pas la valeur de i !)

i ← i + 10

Fin TANT QUE

Version Python avec la boucle bornée FOR

1
2

for i in range(45,200,10):
    faire_un_truc()

Correction ?

...CORRECTION...

Je vais travailler avec la forme TANT QUE.

On voit que i a pour valeur initiale 45 et augmente de 10 à chaque tour de boucle.

On peut donc représenter les valeurs successives que va prendre la variable i par une suite entière arithmétique de valeur intiale 45 et de raison 10.

i_n = 45 + 10*n

On peut donc écrire de cette façon la condition de la boucle TANT QUE :

On part de la condition de départ :

TANT QUE i_n < 200

On remplace la suite i_n par son expression :

TANT QUE (45 + 10*n) < 200

On remarque qu'on a une relation inférieure alors qu'on cherche supérieure. On inverse donc les deux côtés et on modifie la relation.

TANT QUE 200 > (45 + 10*n)

On sait qu'on veut obtenir "supérieur à 0", on va donc transférer les termes de droite dans les termes de gauche :

TANT QUE (200 - 45 - 10*n) > 0

On obtient

TANT QUE (155 - 10*n) > 0

Nous pouvons maintenant conclure car :

On dispose bien qu'une expression TANT QUE VARIANT > 0
dans laquelle VARIANT = 155 - 10*n est bien une suite d'entiers strictement décroissante puisque la raison vaut -10.

(1) + (2) démontre donc que la boucle se termine.

Regardons maintenant notre algorithme de tri.

POUR i variant de 1 à (longueur - 1) inclus

cle ← t[i]

j ← i - 1

TANT QUE j ≥ 0 et que t[j] > cle

t[j+1] ← t[j]

j ← j - 1

Fin TANT QUE

t[j+1] ← cle

Fin POUR

Renvoyer VIDE (∅)

On voit qu'il y a une boucle (TANT QUE) à l'intérieur d'une autre boucle (POUR).

Prouver la terminaison de l'algorithme demande donc de prouver la terminaison de chacune de ces boucles.

Commençons par la boucle TANT QUE interne.

On ne tiendra compte ici que d'une des façons de sortir de la boucle TANT QUE : si la boucle se termine avec une condition, elle se terminera aussi si on lui donne une autre façon d'arrêter :

Continuer TANT QUE ( A ET B ) ⇔ Arrêter lorsque ( (NON A) OU (NON B) )

Cela vient des lois logiques de de Morgan :

NON ( A ET B ) ⇔ ( (NON A) OU (NON B) )

02° Montrer la terminaison de la boucle TANT QUE simplifiée.

TANT QUE j ≥ 0

t[j+1] ← t[j]

j ← j - 1

Fin TANT QUE

Correction ?

...CORRECTION...

Pour prouver qu'une boucle non bornée (Tant que) s'arrête, il faut montrer

la boucle s'exprime sous la forme TANT QUE VARIANT > 0
avec un VARIANT de boucle pouvant s'écrire comme une suite u_n strictement décroissante d'entiers.

Ici, nous avons ceci :

TANT QUE j ≥ 0

t[j+1] ← t[j]

j ← j - 1

Fin TANT QUE

Nous avons bien directement une relation supérieure (ou égale) et un zéro dans le terme de droite.

On voit donc qu'on a une suite arithmérique de raison -1 avec une valeur initiale j_O supérieure ou égale à 0.

On peut donc écrire que j_n = j_O - n.

On voit directement que j est le VARIANT permettant d'écrire TANT QUE VARIANT > 0.

On peut ainsi écrire :

TANT QUE j_n ≥ 0
TANT QUE j_n > -1
TANT QUE j_O - n > -1
TANT QUE j_O + 1 - n > 0

Nous pouvons maintenant conclure car :

On dispose bien qu'une expression TANT QUE VARIANT > 0
dans laquelle VARIANT = (j_O + 1) - 1*n est bien une suite d'entiers strictement décroissante puisque la raison vaut -1.

(1) + (2) démontre donc que la boucle se termine.

Il nous reste à gérer le cas de la boucle FOR externe. Comme il s'agit d'une boucle FOR, on vérifie facilement qu'elle s'arrête : on part de 1, on gagne 1 à chaque tour de boucle et on s'arrête lorsqu'on dépasse la valeur maximale.

Nous allons en profiter néanmoins pour réviser les équivalences entre un POUR et un TANT QUE.

03° Montrer la terminaison de la boucle FOR ci-dessous que nous avons transformé en boucle WHILE.

POUR i variant de 1 à (longueur - 1) inclus

cle ← t[i]

j ← i - 1

...

t[j+1] ← cle

Fin POUR

Elle est équivalente à cette boucle :

i ← 1

TANT QUE i < longueur

...

i ← i + 1

...

Fin TANT QUE

Correction ?

...CORRECTION...

On peut donc écrire la variable de boucle sous la forme suivante :

i_n = 1 + n.

Cela revient à écrire :

TANT QUE i_n < longueur

TANT QUE longueur > i_n

TANT QUE longueur > (1 + n)

TANT QUE (longueur - 1 - n) > 0

TANT QUE ( (longueur - 1) - n) > 0

Nous pouvons maintenant conclure car :

On dispose bien qu'une expression TANT QUE VARIANT > 0
dans laquelle VARIANT = (longueur - 1) - 1*n est bien une suite d'entiers strictement décroissante puisque la raison vaut -1.

(1) + (2) démontre donc que la boucle se termine.

3 - Coût du tri par insertion

⇩ ⇧ ⤊

Nous allons maintenant étudier la complexité de notre algorithme

dans le meilleur des cas et
dans le pire des cas.

Pour cela, nous allons regarder le nombre de comparaisons pour un tableau possède n éléments.

Dans le meilleur des cas

Pour cet algorithme, c'est quand le tableau est déjà trié dans le bon ordre !

04° Utiliser l'animation ci-dessous qui correspond au tri par insertion d'une liste déjà triée en ordre croissant.

Pour caractériser la complexité (le coût) de cet algorithme, on choisit d'étudier le nombre de comparaisons qu'il effectue.

Répondre à la question suivante :

QCM : Dans le meilleur des cas, que peut-on écrire de la complexité du tri par insertion ?

A : Elle est logarithmique (𝞗(lg n) ), c'est à dire que la complexité évolue moins vite que le nombre n de données. Exemple : si on multiplie les données par 8, on ne rajoute que 3 opérations.
B : Elle est linéaire ( 𝞗(n) ), c'est à dire que la complexité évolue comme le nombre n de données (par exemple : si on multiplie le nombres de données n par 8, le temps d'exécution est multiplié par 8)
C : Elle est quadratique ( 𝞗(n²) ), c'est à dire que la complexité évolue comme le carré du nombre n de données (par exemple : si on multiplie le nombres de données n par 8, le temps d'exécution est multiplié par 64, 10*10)
D : Elle est exponentielle ( 𝞗(xⁿ) ), c'est à dire que la complexité évolue à terme beaucoup plus vite que n'importe quelle fonction polynomiale du nombre n de données (par exemple : si on passe de 10 à 80 données (x8), le temps d'exécution est multiplié par 10²¹ !)


Indice	00	01	02	03	04	05	06	07	08	09	10	11	12	13	14	15	16	17	18	19
Elément	21	22	27	28	33	35	36	37	38	42	44	45	46	50	51	59	66	82	87	96

Correction ?

...CORRECTION...

On remarque sur l'animation qu'il faut 19 comparaisons pour finir l'algorithme de tri des 20 éléments.

Avec 1000 éléments, nous aurions 9999 comparaisons à faire.

Le nombre de comparaisons est donc une fonction f(n) telle que f(n) = n - 1

Pour les grandes valeurs de n, le 1 devient totalement négligeable.

On voit donc que la complexité dans le meilleur des cas est linéaire.

On répondra donc

B : Elle est linéaire ( 𝞗(n)), c'est à dire que la complexité évolue comme le nombre n de données (par exemple : si on multiplie le nombres de données n par 100, le temps d'exécution est multiplié par 100)

Le pire des cas

Regardons maintenant le pire des cas pour cet algorithme. Nous allons voir qu'il s'agit du cas où la liste est triée dans le mauvais sens.

La boucle POUR ne pose pas de problème : dans tous les cas, on doit effecuter chacune de ses boucles.

C'est la boucle TANT QUE qu'il faut étudier : parfois elle dure longtemps, parfois non :

TANT QUE j ≥ 0 et que t[j] > cle

t[j+1] ← t[j]

j ← j - 1

Fin TANT QUE

Le TANT QUE possède deux conditions : si la clé est systématiquement plus petite que les éléments du sous-tableau, on va devoir lire un à un tous les éléments du sous-tableau. Jusqu'à atteindre l'élément d'indice 0. C'est le cas le plus défavorable en terme de temps d'exécution.

Si on réflechit un peu, ce cas correspond à un tableau trié mais en sens inverse du sens voulu !

Voici un exemple du pire des cas :


Indice	00	01	02	03	04	05	06	07	08	09	10	11	12	13	14	15	16	17	18	19
Elément	96	87	82	66	58	51	50	46	45	44	42	38	37	36	35	33	28	27	22	21

Sur ce tableau de 20 éléments, la clé va prendre 19 positions successives, de l'indice 1 jusqu'à l'indice 19.

Sur un tableau de n éléments, la clé va prendre n-1 positions successives, de l'indice 1 jusqu'à l'indice n-1.

05° Utiliser l'animation pour répondre à ces questions : dans le pire des cas

combien de comparaisons à l'étape 1 (lorsque la clé est l'indice 1)
combien de comparaisons à l'étape 2 (lorsque la clé est l'indice 2)
combien de comparaisons à l'étape 3 (lorsque la clé est l'indice 3)
combien de comparaisons à l'étape n-1 (lorsque la clé est l'indice n-1)

Correction ?

...CORRECTION...

On voit qu'à l'étape 1, il y aura 1 comparaison à faire.

On voit qu'à l'étape 2, il y aura 2 comparaisons à faire.

On voit qu'à l'étape 3, il y aura 3 comparaisons à faire.

On voit qu'à l'étape n-1, il y aura n-1 comparaisons à faire.

Facile non ?

Du coup, dans le pire des cas, combien doit-on faire de comparaisons pour trier le tableau de n éléments ?

Sur un tableau de n = 6 éléments, on devra donc calculer le nombre de comparaisons C₆ en faisant la somme de 5 nombres :

C₆ = 1 + 2 + 3 + 4 + 5

Sur un tableau de n éléments, on devra donc calculer le nombre C_n de comparaisons en faisant la somme de (n-1) éléments variant de 1 à (n-1) :

C_n = 1 + 2 + 3 + 4 + 5 + ... + (n-5) + (n-4) + (n-3) + (n-2) + (n-1)

La somme C_n est ce qu'on nomme une série.

Que vaut-elle ?

Le mathématicien-astronome-physicien allemand Gauss, surnommé le Prince des Mathématiciens, avait trouvé (en 1786, alors qu'il avait 9 ans dit-on) une méthode séduisante de résolution.

Portrait de Carl Friedrich Gauss, image libre de droit

Recherche d'une formule associée à notre série 1+2+3+4...+n-2 +n-1

Notre série C_n est la somme des (n-1) éléments du membre de droite :

C_n = 1 + 2 + 3 + ... + (n - 3) + (n - 2) + (n - 1)

Nous voudrions associer les éléments deux par deux, mais il est possible qu'ils soient en nombre impair. Comment faire ?

Multiplier chacun des membres par deux !

2 * C_n = 1 + 1 + 2 + 2 + 3 + 3 + ... + (n - 3) + (n - 3) + (n - 2) + (n - 2) + (n - 1) + (n - 1)

2 C_n est la somme de 2(n-1) éléments et nous sommes certain qu'il y a un nombre pair d'éléments.

Si on les associe deux par deux, nous allons obtenir (n-1) couples de deux éléments.

Associons les éléments deux par deux, par complément comme 3 + (n - 3).

2 * C_n = 1 + (n - 1) + 1 + (n - 1) + 2 + (n - 2) + 2 + (n - 2) + 3 + (n - 3) + 3 + (n - 3) + ...

2 * C_n = (1 + n - 1) + (1 + n - 1) + (2 + n - 2) + (2 + n - 2) + (3 + n - 3) + (3 + n - 3) + ...

2 * C_n = (n) + (n) + (n) + (n) + (n) + (n) + ...

Nous avons donc (n-1) valeurs qui valent tous n.

On peut donc écrire

2*C_n = (n-1)n

Au final, cela donne donc :

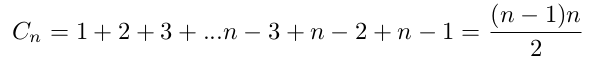
Comme cette somme est aussi longue à écrire, on utilise parfois la notation ci-dessous qui veut dire exactement la même chose :

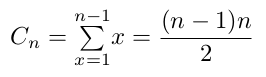formule 1

06° Utiliser le programme Python ci-dessous pour vérifier que la formule est bien valide.

def somme(n):
    """Renvoie 1 + 2 + 3 + ... + n-1"""
    addition = 0
    for x in range(n):
        addition = addition + x
    return addition
 
def formule(n):
    """Renvoie n(n-1)//2"""
    return n*(n-1)//2
 
for n in range(1,101,1):
    print(f"Calcul direct : {somme(n)} contre Formule : {formule(n)}")

07° Nous venons de voir que le nombre de comparaisons nécessaires au tri d'un tableau de n éléments était ceci dans le pire des cas :

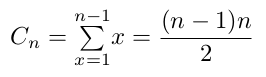formule 1

Question : dans le pire des cas, la complexité du tri par insertion est :

A : logarithmique (𝞗(lg n) ), c'est à dire que la complexité évolue moins vite que le nombre n de données. Exemple : si on multiplie les données par 8, on ne rajoute que 3 opérations.
B : linéaire ( 𝞗(n) ), c'est à dire que la complexité évolue comme le nombre n de données (par exemple : si on multiplie le nombres de données n par 8, le temps d'exécution est multiplié par 8)
C : quadratique ( 𝞗(n²) ), c'est à dire que la complexité évolue comme le carré du nombre n de données (par exemple : si on multiplie le nombres de données n par 8, le temps d'exécution est multiplié par 64, 10*10)
D : exponentielle ( 𝞗(xⁿ) ), c'est à dire que la complexité évolue à terme beaucoup plus vite que n'importe quelle fonction polynomiale du nombre n de données (par exemple : si on passe de 10 à 80 données (x8), le temps d'exécution est multiplié par 10²¹ !)

Correction ?

...CORRECTION...

Démonstration de la complexité du pire des cas

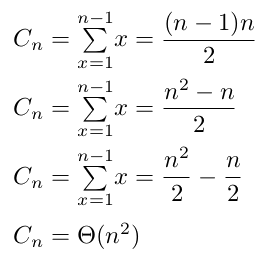
Quelques explications si ce n'est pas suffisant.

On cherche à voir uniquement le comportement global de cet algorithme lorsqu'on augmente les données qu'il doit traiter.

On va donc simplifier notre formule : le but est de savoir à quelle type de fonction se rapproche le coût de notre algorithme, pas la formule exacte de cette fonction (nous l'avons déjà !).

Complexité du tri par insertion

On retiendra donc que :

Dans le meilleur des cas, la complexité du tri par insertion est 𝞗(n) : le coût est linéaire.
Dans le pire des cas, la complexité du tri par insertion est 𝞗(n²) : le coût est quadratique.

Si on veut juste parler de la complexité dans tous les cas, on peut donc dire qu'elle est quadratique ou moins selon les cas. On retrouve donc la notation suivante par exemple : 𝞞(n²)

Ce que nous ne verrons pas cette année est le cas moyen. Pour l'instant, on ne peut pas dire grand chose du cas moyen. Et on ne sait pas si le pire des cas arrive souvent, ou pas...

D'où la grande contribution des mathématiques à cette partie du programme.

Ceux qui ont pris la spécialité Math ont surement rencontré la notion de série.

Voir

Pour faire le lien avec cette autre spécialité (et ne pas vous demander pourquoi "c'est presque la même formule mais pas vraiment"), remarquez bien qu'ici notre série des comparaisons n'arrive qu'à n-1. La formule qui vous avez vu en math va jusqu'à n.

Voici ce que vous avez certainement rencontré en mathématiques ( et ça peut également servir à ceux qu'y n'ont pas cette spécialité) :

Série arithmétique des nombres de 1 à n

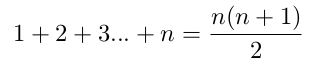
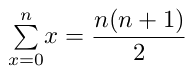formule 1'

Cela correspond bien à notre formule 1 avec un changement de variable n = n' -1.

Série arithmétique des carrés de 1² à n²

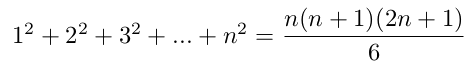
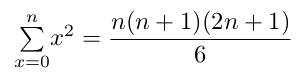formule 2

Série arithmétique des cubes de 1³ à n³

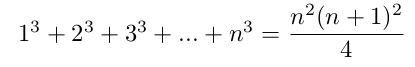
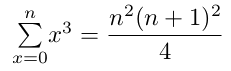formule 3

Série géométrique (un exemple avec x différent de 0)

Formule de la série géométrique de l'exemple

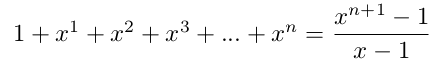
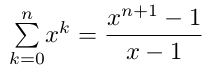formule 4

4 - Preuve de correction

⇩ ⇧ ⤊

Nous avons donc démontré

la terminaison du tri par insertion : nous sommes maintenant certain qu'il va s'arrêter pourvu qu'on lui en laisse le temps
le coût quadratique dans le pire des cas : nous savons que si on multiplie la taille des données par 10, le temps d'exécution va approximativement être multiplié par 100.

Oui mais... Est-ce que notre algorithme marche à chaque fois. Après tout, nous avons fait quelques essais, rajouté quelques doctests. Mais il y a peut-être des cas (même rares) qui risquent de créer un raté. Non ?

Imaginez : vous avez la responsabilité d'un grand nombre de vie en travaillant sur un algorithme de pilotage automatique. L'un des processus que vous avez créé utilise un tri par insertion. S'il disfonctionne, c'est la perte de contrôle de l'appareil. Vous avez fait des tests. Vous savez que ça marche. Mais... Laisseriez-vous l'appareil décoller sans être certain que ça fonctionne toujours ?

Test ≠ Correction

A toujours avoir en tête : on ne peut pas prouver la correction d'un algorithme en réalisant juste un très grand nombre de tests : nous ne parviendrions qu'à prouver que l'algortihme fonctionne dans tous les cas testés mais pas dans tous les cas possibles.

Prouver la correction d'un algorithme veut dire qu'il est correct dans dans tous les cas.

Attention, tous les cas qui vérifient bien les spécifications d'entrée. Si quelqu'un envoie n'importe quoi à votre fonction

ce n'est pas un problème de la correction de l'algorithme,
c'est un problème de filtrage des données reçues.

Voyons comment apporter la preuve de correction d'un algorithme : démontrer qu'il renvoie une réponse correcte dans tous les cas légitimes. Cela revient à dire que l'algorithme est juste.

Preuve de correction et invariant

Définitions

La preuve de correction d'un algorithme permet d'affirmer

qu'il fournit toujours une réponse correcte
sur toutes les entrées valides qu'on lui fournit.

Pour faire la preuve de correction d'un algorithme, il faut trouver un INVARIANT : une propriété P vérifiable qui reste vraie lors des différentes étapes de l'algorithme.

Un INVARIANT DE BOUCLE est une propriété VRAIE à chaque début de tour, juste avant l'exécution de la première instruction de la boucle.

Cet invariant permettra de prouver que le résultat final après exécution est bien le résultat attendu.

Malheureusement, il n'y a pas de méthodologie automatique miraculeuse pour trouver cet invariant. Il faut réfléchir et tenter des choses, comme avec toute démonstration.

Démonstration en 3 phases : Initialisation-Conservation-Terminaison

Une fois qu'on dispose d'un INVARIANT P, la démonstration se fait en trois temps.

Phase d'initialisation : P₀ est VRAI

On doit prouver que l'INVARIANT est VRAI lorsqu'on commence le premier tour de boucle mais sans l'avoir réalisé en entier. On a donc fait 0 tour en entier.

Le plus souvent, cette partie est triviale. Mais pas toujours...

Phase de conservation : P_k ➡ P_k+1

SI P est vrai après k tours de boucles, ALORS P sera encore vrai en ayant fait un tour de boucles supplémentaire.

Hypothèse de départ :

On fait l'hypothèse qu'on a fait k tours de boucles et qu'on est au début du tour k+1. L'INVARIANT P_k est donc considéré juste.

Déroulement du tour de boucle (k+1) jusqu'au début du prochain

On doit montrer qu'en réalisant ce tour complétement jusqu'au début du prochain, l'invariant P reste vrai à la fin de cette boucle. On aura donc fait k+1 tours de boucle complet, P_k+1 serait encore vérifiée.

On se place dans le cadre d'un tour qui est suivi d'un autre tour. On ne se place pas dans le cadre de la toute dernière boucle ici. On boucle, point.

On peut donc écrire P_k ➡ P_k+1

Phase de terminaison

On doit y prouver qu'à la fin du dernier tour, on obtient la situation voulue. Ni trop tôt, ni trop tard. C'est pour cela qu'on nomme cette partie la phase de terminaison, à ne pas confondre avec la preuve de terminaison.

P₀ ➡ P₁ ➡ P₂ ➡ P₃... ➡ P_final

Comme dit plus haut, le problème est qu'il n'existe pas de méthode automatique pour trouver le bon invariant. Il faut chercher à chaque nouveau problème qui se pose...

Regardons le cas du tri par insertion.

Le principe est simple : on décompose le problème

en un sous-tableau trié (qui gagne un élément à chaque fois) et
en un sous-tableau non-trié (qui perd un élément à chaque fois)

Invariant du tri par insertion

Initialement, le sous-tableau trié ne contient qu'une valeur.
On peut considérer que cet élément unique est trié par rapport à lui-même...

A chaque tour de boucle, on va rajouter un élément à ce sous-tableau.

On considère que notre INVARIANT pourrait être la propriété P_k suivante :

Après k tours de boucle, k+1 éléments sont triés dans le sous-tableau [0;k] de gauche.

Dans le sous-tableau trié par ordre croissant ici, on doit donc avoir
t[x] < t[x+1] pour toute valeur d'indice x dans [0; k-1].

08° Travaillons sur l'initialisation.

Avant de rentrer dans la boucle (k=0), notre sous-tableau trié ne contient que la première valeur.

Peut-on considérer que l'invariant P_k est vérifié pour k = 0 ?

Correction ?

...CORRECTION...

On peut sans peine se convaincre qu'un sous-tableau ne contenant qu'un élément unique est bien trié.

P_k correspond à cette proposition :

Après k tours de boucle, k+1 éléments sont triés dans le sous-tableau [0;k] de gauche.

P₀ correspond donc à :

Après 0 tours de boucle, 1 élément est trié dans le sous-tableau [0;0] de gauche.

La propriété P₀ est donc vérifiée.

Nous venons de prouver l'initialisation : P₀ est VRAI.

Passons maintenant à la conservation. Pour rappel, voici l'algorithme :

Algorithme du tri par insertion

POUR i variant de 1 à (longueur - 1) inclus

cle ← t[i]

j ← i - 1

TANT QUE j ≥ 0 et que t[j] > cle

t[j+1] ← t[j]

j ← j - 1

Fin TANT QUE

t[j+1] ← cle

Fin POUR

Renvoyer VIDE (∅)

09° Quelle va être la première valeur prise par i lors du premier tour de boucle ? Que vaut j avant de rentrer dans le TANT QUE ?

Quelle est la relation entre le nombre de tours de boucle k et la valeur de la variable de boucle i ?

Correction ?

...CORRECTION...

POUR i variant de 1 à (longueur - 1)

Lors du premier tour, i vaut donc 1 et j vaut 0 puisqu'on retire un.

On voit donc qu'on peut écrire k = i.

Considérons que la propriété P_k est VRAI : à la fin des k tours de boucle, le sous-tableau [0;k] est trié et contient donc k+1 éléments.

Regardons si cela implique P_k+1.

Au tout début du tour de boucle k+1 suivant

l'indice i est égal à k+1
on dispose d'un sous-tableau [0;k] trié auquel
on va rajouter un nouvel élément, la clé t[k+1]

Cas étudié n°1 :

On considère que cle correspondant initialement à t[k+1] est inférieure à tous les éléments du sous-tableau trié [0;k].

Exemple : si on débute la boucle k+1=5, cela veut dire

qu'on va rajouter l'élément d'indice i=5 et
que le sous-tableau est trié sur [0;4]

[10, 20, 30, 40, 5]

10° Plusieurs questions progressives pour vous montrer qu'on va parvenir à prouver que P_k est VRAI :

Comment l'algorithme va-t-il déplacer les éléments du sous-tableau trié [0; k] si la cle (le 5 en rouge ici) est inférieure à tous les éléments déja triés ?
Quels vont être les nouveaux indices extrêmes des éléments initialement dans [0;k] après placement de la clé ?
Les éléments ainsi déplacés seront-ils encore triés entre eux ?
A quel indice du tableau va alors être placée la clé ?
Puisque les anciens éléments triés ont été déplacés en [1;k+1], qu'est-ce qui permet d'affirmer que le sous-tableau [0; k+1] est trié à la fin de cette boucle ?

Correction ?

...CORRECTION...

La lecture du TANT QUE permet de voir qu'on décale alors juste tous les éléments d'une case vers la droite.

Les éléments de [0;k] vont se retrouver dans [1;k+1].

Comme on les décale tous d'une case uniquement, cela ne change rien à leur ordre relatif : ils restent triés entre eux.

On sort avec un j valant -1 mais le placement de la clé se faisant avec la ligne t[j+1] ← cle, on voit qu'on placera la clé à l'indice 0.

La clé (plus petite que tous les autres éléments) vient d'être placée en indice 0.

On peut donc affirmer que le tableau [0;k+1] est maintenant trié en ordre croissant.

CONCLUSION : P_k+1 est VRAI.

Nous venons donc de montrer que sur le cas particulier d'une clé inférieure à tous les éléments, P_k implique bien P_k+1 après un tour de boucle en plus.

Cas étudié n°2 :

On considère maintenant que la cle initialement en t[k+1] est supérieure à tous les éléments du sous-tableau trié [0;k].

Exemple: si on débute la boucle pour k+1=5, cela veut dire qu'on va rajouter l'élément d'indice i=5 et que le sous-tableau est trié sur [0;4]
[10, 20, 30, 40, 50]

11° Sur le même principe de raisonnement que les questions précédentes, montrer la conservation de la propriété P_k+1 sous-tableau trié si la clé d'indice k+1 est supérieure à tous les éléments du sous-tableau [0, k].

Correction ?

...CORRECTION...

C'est encore plus simple :

On ne rentre même pas dans le TANT QUE puisque l'une des condition n'est pas bonne :

TANT QUE j ≥ 0 et que t[j] > cle

Si j vaut i-1 mais qu'on place la clé avec t[j+1] ← cle, on voit qu'on laisse la clé au même indice i.

Le sous-tableau [0, k] était trié et on ne le transforme pas.

On rajoute la clé (un élément plus grand que les autres) à l'indice k+1.

On obtient donc bien un sous-tableau [0; k+1] trié après application d'un tour de boucle POUR supplémentaire.

CONCLUSION : P_k+1 est VRAI.

Nous venons donc de montrer que sur le cas particulier d'une clé supérieure à tous les éléments du sous-tableau trié, P_k implique bien P_k+1 après un tour de boucle en plus.

Il reste à expliquer ce que se passe lorsque la clé est inférieure à certains éléments à sa gauche, mais pas tous.

Cas étudié n°3 :

Cette fois, la cle initialement en t[k+1] est inférieure à certains éléments du sous-tableau trié [0;k]

Exemple: si on débute la boucle pour k+1=5, cela veut dire

qu'on va rajouter l'élément d'indice i=5 et
que le sous-tableau est trié sur [0;4]

[10, 20, 30, 40, 25]

Revoici l'algorithme.

POUR i variant de 1 à (longueur - 1) inclus

cle ← t[i]

j ← i - 1

TANT QUE j ≥ 0 et que t[j] > cle

t[j+1] ← t[j]

j ← j - 1

Fin TANT QUE

t[j+1] ← cle

Fin POUR

Renvoyer VIDE (∅)

12° On considère que

Tous les éléments d'indice [m;k] sont supérieurs à la clé.
Tous les éléments d'indice [0;m-1] sont inférieurs ou égaux à la clé.

Questions

Quels sont les éléments du sous-tableau [0;k] qui auront bougés une fois sorti du TANT QUE ?
Ces éléments sont-ils encore triés ?
A quel indice va alors être placée la clé ?
Peut-on encore dire que le sous-tableau [0;k] est trié, sachant que

Le sous-tableau [0; m-1] est toujours trié et ses éléments inférieurs ou égaux à la clé.
Le sous-tableau [m+1;k+1] est toujours trié et ses éléments supérieurs ou égaux à la clé.

Correction ?

...CORRECTION...

Le sous-tableau va être divisé en deux parties : les éléments qui n'auront pas bougé et les éléments qui auront bougé.

Regardons d'abord la partie modifiée.

TANT QUE j ≥ 0 et que t[j] > cle

La seconde condition ne sera vraie que jusqu'à t[m] > cle.

On déplace d'une case à droite les éléments [m; k] qui vont se retrouver en [m+1; k+1].

Par contre, le sous-tableau [0;m-1] ne sera pas modifié.

Comme les éléments sont tous décalés d'une case, on garde leur tri relatif.

Regardons le placement de la clé.

t[j+1] ← cle

Puisque j contient m-1, on va placer la clé à l'indice m-1+1, soit m.

Le sous-tableau [0; m-1] est trié et inférieur ou égal à la clé.
La clé est à l'indice m.
Le sous-tableau [m+1;k+1] est trié et supérieur ou égal à la clé.

Nous pouvons donc affirmer que le sous-tableau [0; k+1] est bien trié après avoir appliqué un tour de boucle supplémentaire.

CONCLUSION : P_k+1 est VRAI.

Avec nos k+1 tours de boucle, nous avons fait les trois cas possibles pour le placement de la clé par rapport aux éléments du sous-tableau initial [0;k].

Dans les trois cas, nous avons pu affirmer que :

si le sous-tableau [0; k] est bien trié après k tours de boucle
le sous-tableau [0; k+1] est trié après avoir appliqué ce nouveau tour de boucle

Nous sommes donc partis de P_k :

Après k tours de boucle, k+1 éléments sont triés dans le sous-tableau [0;k] de gauche.

Nous obtenons bien à chaque fois cette proposition :

Après k+1 tours de boucle, k+2 éléments sont triés dans le sous-tableau [0;k+1] de gauche.

Nous avons donc démontré la conservation de l'invariant : P_k ➡ P_k+1

La dernière étape est ici assez rapide :

Terminaison

En regardant la boucle, on voit que i vaut 1 au départ et atteint longueur - 1 lors du dernier tour de boucle.

Notre algorithme aura donc fait longueur - 1 tours de boucle.

Or l'invariant P_k est la propriété selon laquelle, après k tours de boucle,

le sous-tableau trié est [0;k] et
le sous-tableau contient donc k + 1 éléments triés

A la fin de l'algorithme, k va donc valoir longueur-1.

Le nombre d'éléments triés correctement est donc :

k + 1 élements triés
= longueur-1 + 1 élements triés
= longueur élements triés

Et ça tombe bien : après le dernier tour de boucle, le sous-tableau trié contient donc longueur éléments : tout le tableau !

Nous avons donc montré la terminaison : l'algorithme agit bien sur toutes les données.

Nous avons donc pris l'INVARIANT P_k suivant :

Après k tours de boucle, k+1 éléments sont triés dans le sous-tableau [0;k].

Avec cette INVARIANT P, nous avons montré :

son initialisation : P₀ est VRAI
sa conservation : P_k ➡ P_k+1
sa terminaison : on a bien traité tout le tableau

Conclusion : nous avons prouver la correction de l'algorithme du tri par insertion.

Cet algorithme fonctionne donc dans tous les cas valides, c'est à dire tous les cas où le tableau reçu respecte bien les préconditions fournies.

5 - Exemple avec Python

⇩ ⇧ ⤊

Pour finir, nous allons montrer comment faire planter un programme si on ne respecte pas une condition qui devrait être respectée !

C'est le principe de la programmation offensive : on ne donne pas simplement les préconditions, on empêche la fonction d'agir si les préconditions ne sont pas correctes. Dit autrement : on préfère faire "planter" le programme avant qu'il ne stocke des données erronnées et ne réalise des choses potentiellement dangereuses avec celles-ci.

✎ 13° Utiliser le programme ci-dessous.

Quelle est la valeur maximale qu'on veut imposer à a et b ?

def addition(a, b):
    """Additionne a et b pourvu que a et b ne soient pas strictement supérieure à 10
    :: param a(int) : un nombre entre 0 et 10
    :: param b(int) : un nombre entre 0 et 10
    :: return (int) : la somme de a et b
    """
    return a + b

Que donnent les instructions suivantes ? Est-ce un problème de ne pas respecter les préconditions sur a et b ?


>>> addition(5,10)
 
>>> addition(5,25)

Comme vous l'avez vu, les préconditions ne sont ici que de la documentation. Si la personne qui utilise la fonction ne veut pas la respecter, elle peut le faire.

Oui mais... si l'addition vise à créer une note sur 20 à partir de deux notes sur 10. Ca va renvoyer n'importe quoi.

Et bien, nous pourrions faire "planter" le programme en créant une exception si les valeurs de a et b ne sont pas bonnes.

Pour cela, nous allons créer des assertions, c'est à dire des expressions qui devraient être évaluées à True.

Si ce n'est pas le cas, ça stoppe le programme en lançant une exception et affiche le message d'erreur voulu par l'utilisateur.

✎ 14° Utiliser le programme ci-dessous.

Quelle est la valeur maximale qu'on veut imposer à a et b ?

def addition2(a, b):
    """Additionne a et b pourvu que a et b ne soient pas strictement supérieure à 10
    :: param a(int) : un nombre entre 0 et 10
    :: param b(int) : un nombre entre 0 et 10
    :: return (int) : la somme de a et b
    """
    assert a <= 10, "a est trop grand ! On avait dit 10 au maximum dans la documentation !"
    assert b <= 10, "b est trop grand ! On avait dit 10 au maximum dans la documentation !"
    return a + b

Que donnent les instructions suivantes ? Est-ce un problème de ne pas respecter les préconditions sur a et b ?


>>> addition2(5,10)
 
>>> addition2(5,25)

Cette fois, la seconde addition a provoqué un message d'erreur à cause du non-respect de l'assertion. Un truc du genre :


    assert b <= 10, "b est trop grand ! On avait dit 10 au maximum dans la documentation !"
AssertionError: b est trop grand ! On avait dit 10 au maximum dans la documentation !

Vu comme ça, ça à l'air un peu bête de faire planter volontairement son programme mais si le code n'est pas encore finalisé et vous voulez savoir ce qui fonctionne ou pas, cela est pratique.

Aujourd'hui, nous allons simplement finir en utilisant ces assertions pour vérifier que notre invariant est bien un invariant sur quelques exemples.

Comme l'invariant est la propriété d'un sous-tableau d'être trié, nous allons créer une fonction est_trie() qui vérifie cela.

On remarque bien la présence, ligne 25, d'une assertion à la fin de la boucle POUR de façon à vérifier si l'invariant est toujours vérifié.

def tri_par_insertion(t):
    """Tri en ordre croissant le tableau en utilisation le tri par insertion
 
    :: param t(list) :: un tableau d'éléments de même type
    :: return (None) :: procédure (renvoie donc None en Python)
    .. Effet de bord :: modifie le tableau en permutant les éléments
 
    :: precondition :: t doit contenir au moins deux éléments
    :: precondition :: les éléments de t doivent pouvoir être comparés entre eux
 
    :: exemple ::
    >>> numeros = [5, 8, 1, 20, 15]
    >>> tri_par_insertion(numeros)
    >>> numeros    
    [1, 5, 8, 15, 20]
 
    """
    for i in range(1, len(t)):
        cle = t[i]
        j = i - 1 # On commence par l'élément juste à gauche de la clé
        while j >= 0 and t[j] > cle:
            t[j+1] = t[j] # On décale l'élément vers la droite
            j = j - 1 # On passe à l'élément encore à gauche
        t[j+1] = cle
        assert est_trie(t, i), "L'invariant n'est pas vérifié : le sous-tableau n'est pas trié"
 
def est_trie(t, k):
    """Renvoie True si le sous-tableau [0;k] est trié dans l'ordre croissant"""
    if len(t) < 2:
        return True
    for i in range(k):
        if t[i] > t[i+1]:
            return False
    return True
 
if __name__ == '__main__':
    import doctest
    doctest.testmod()

15° Testons la fonction est_trie() : elle renvoie True si le tableau est bien trié par ordre croissant de l'indice 0 à l'indice k inclus.


>>> est_trie([10,20,30,40],2)
 
>>> est_trie([10,20,40,30],2)
 
>>> est_trie([20,10,30,40],2)

Questions :

Expliquer en français comment fonctionne cette fonction.
Quel est le défaut de cette fonction d'un point de vue algorithmique ?
Pourquoi ne pas avoir créer une fonction totalement correcte d'un point de vue algorithmique ?

Correction ?

...CORRECTION...

A chaque fois, on transmet un indice 2. Cela veut dire qu'on observe les indices 0, 1 et 2, soit les trois premiers nombres.


>>> est_trie([10,20,30,40],2)
True
 
>>> est_trie([10,20,40,30],2)
True
 
>>> est_trie([20,10,30,40],2)
False

Expliquer en français comment fonctionne cette fonction.

Si le tableau contient 0 ou 1 élément, on répond que le tableau est trié (et on sort définitivement).

Pour chaque indice allant de 0 à k-1 (avant dernier élément donc), on répond FAUX si on constate que cet élément est plus grand que le suivant (et on sort définitivement).

Si on arrive à la fin, c'est que tous les éléments étaient bien placés. On répond donc VRAI.

Quel est le défaut de cette fonction d'un point de vue algorithmique ?

Elle possède trois portes de sortie. Il sera donc compliqué de vérifier sa correction.

Pourquoi ne pas avoir créer une fonction totalement correcte d'un point de vue algorithmique ?

Ne réaliser qu'une réponse finale avec une seule porte de sortie rendrait le code plus lourd. Ici, c'est moins pur mais c'est moins lourd.

16° Tester l'assertion à l'aide de la commande suivante. Si l'invariant est toujours vraie, vous n'aurez jamais d'erreur !


>>> import random
>>> donnees = [random.randint(1,1000) for x in range(100)]
>>> tri_par_insertion(donnees)

Mais attention, ce n'est pas une démonstration. Ici, on montre que ça fonctionne parfois. La vraie démonstration a été faite dans la partie précédente.

En utilisant les flèches HAUT et BAS de votre clavier, vous pouvez retrouver les anciennes instructions pour les exécuter plusieurs fois.

Ca devrait marcher à tous les cas : l'invariant "le sous-tableau [0;i] est trié" est un vrai invariant.

Preuve de correction et jeux de tests

De façon générale, La preuve de correction d'une fonction ne peut pas être obtenu par un jeu de tests aussi grand soit-il.

Cas particulier : si une fonction ne possède qu'un nombre fini de configurations d'entrée et qu'on vérifie que la réponse est bonne pour chacune des configurations, on peut alors vérifier sa correction de cette façon. Mais c'est assez rare comme situation.

17° Si on considère le pire des cas, quel devrait être le rapport entre le temps d'exécution du tri par insertion avec 1000 éléments et 10000 éléments ?

Et dans le meilleur des cas ?

Correction ?

...CORRECTION...

Nous avions vu que le coût dans le pire des cas était quadratique (en n²).

Si on multiplie la taille des données par 10 en passant de 1000 à 10000, nous allons donc multiplier le temps d'exécution théorique par 100.

Dans le meilleur des cas, le coût était linéaire. Si on multiplie la taille des données par 10, on multiplie le temps d'exécution théorique par 10.

✎ 18° Si on considère le pire des cas, quel devrait être le rapport entre le temps d'exécution du tri par insertion avec 1000 éléments et 4000 éléments ?

Et dans le meilleur des cas ?

6 - FAQ

⇩ ⇧ ⤊

Pourquoi justifiez la terminaison d'une boucle FOR ?

Un peu pour l'exercice. Il existe deux cas où une boucle POUR peut mal tourner :

On demande par exemple de commencer à 1, de s'arrêter à 10 et de décrémenter de 1 à chaque tour. Ca donne 1, 0, -1 ... et ça ne s'arrêtera jamais...
On touche à la variable de boucle dans la boucle.

Ici, vous n'avez ni l'un ni l'autre mais ça vous permettra de vous souvenir qu'il faut un peu surveiller les boucles POUR quand même.

Activité publiée le 07 05 2020
Dernière modification : 07 05 2020
Auteur : ows. h.

⏪

⏫

⏩