15 - Chiffrement asymétrique

1 - Pourquoi ne pas se limiter au cas symétrique

⇩ ⇧ ⤊

Nous avons vu le principe du chiffrement / déchiffremment symétrique :

• On chiffre un message m avec une clé et on obtient un message mc chiffré, illible, sauf par ceux qui connaissent la clé.
• On déchiffre le message mc chiffré en utilisant la même clé que lors du chiffrement.


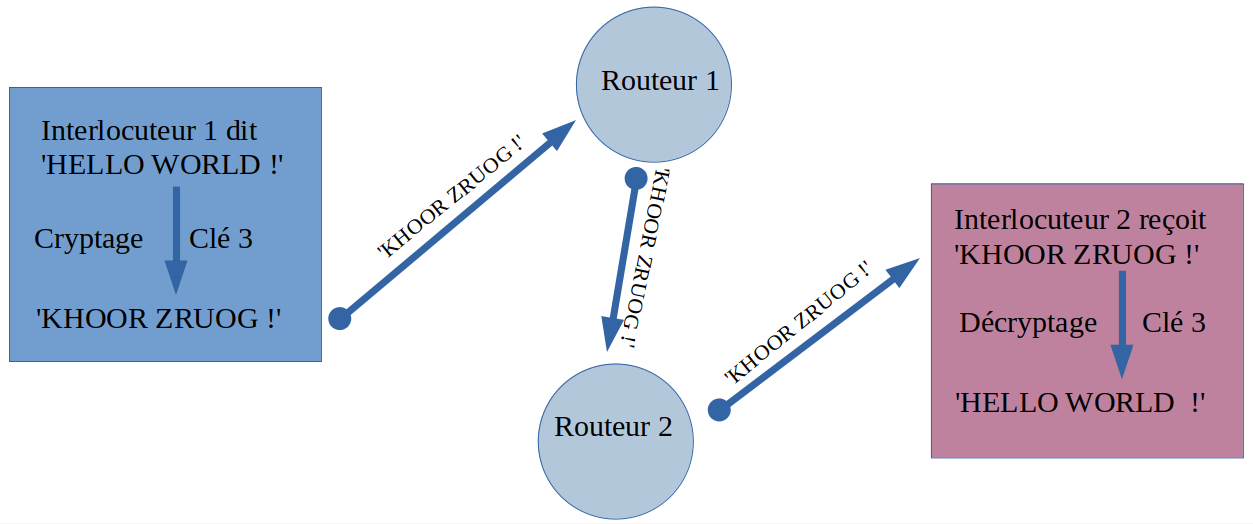
Si la clé de déchiffrement est la bonne, on aura alors md = m.

On remarque donc que les fonctions chiffrer et déchiffrer sont en quelque sorte des fonctions réciproques :

mc = chiffrer(m, cle)  où  mc  est le message chiffré et  m  le message.

m  = dechiffrer(mc, cle)  où  mc  est le message chiffré et  md  le déchiffré.

m  = dechiffrer(chiffrer(m, cle), cle) 

Il y a deux défauts :

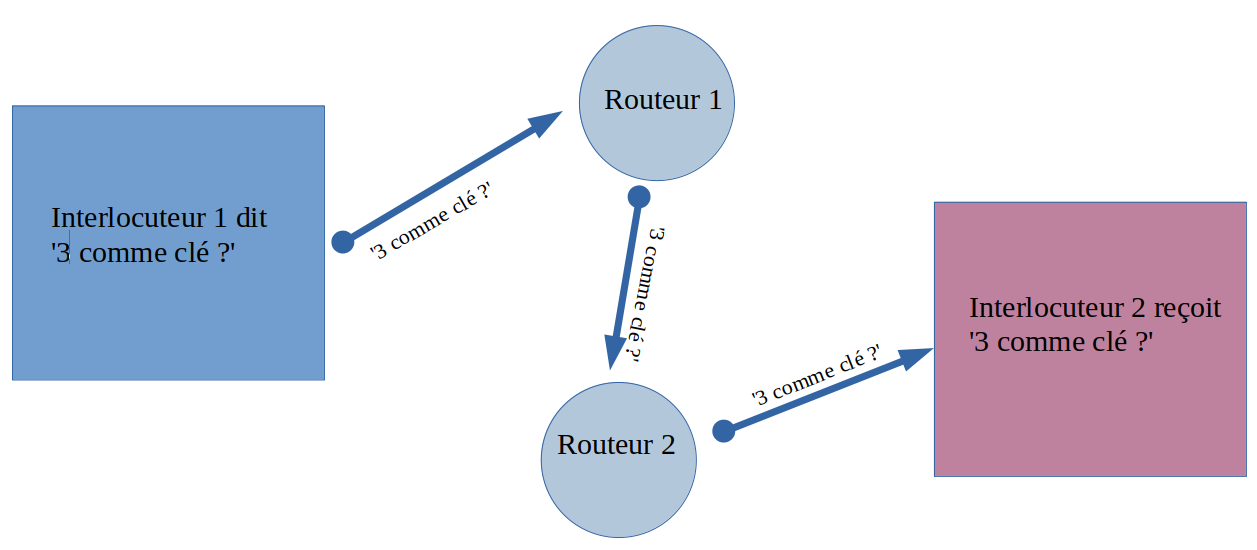
1. On doit partager la clé en clair : la clé pourrait donc se faire intercepter assez facilement lors de la communication initiale.

2. Si on connaît la clé, on peut chiffrer et déchiffrer. L'émetteur peut donc également déchiffrer les autres messages de son interlocuteur s'il partage la même clé.

2 - Principe du chiffrement asymétrique

⇩ ⇧ ⤊

Il y a eu plusieurs types de systèmes de chiffrement asymétrique. Nous verrons ici le principe général le plus connu : le système RSA.

Principe des clés complémentaires : A et B

Le système asymétrique comporte deux clés cleA et cleB complémentaires : leurs valeurs sont différentes mais elles sont reliées par une relation mathématique. Bien entendu, trouver cette relation mathématique ne doit pas être FACILE. Au contraire, retrouvez l'une des valeurs en connaissant l'autre doit être une tâche DIFFICILE.

Le principe est le suivant :

• Si on obtient mca en chiffrant le message avec cleA, il faut utiliser cleB pour déchiffrer le message.

mca = chiffrer(m, cleA)

m   = dechiffrer(mca, cleB)

m   = dechiffrer(chiffrer(m, cleA), cleB) 

m   ≠ dechiffrer(chiffrer(m, cleA), cleA) 

• Si on obtient mcb en chiffrant le message avec cleB, il faut utiliser cleA pour déchiffrer le message.

mcb = chiffrer(m, cleB)

m   = dechiffrer(mcb, cleA)

m   = dechiffrer(chiffrer(m, cleB), cleA) 

m   ≠ dechiffrer(chiffrer(m, cleB), cleB) 

Analogie du coffre

C'est un peu comme si nous pouvions réaliser une porte de coffre qu'on peut uniquement fermer avec une clé A. Une fois le coffre fermé, on ne pourra l'ouvrir qu'avec la clé B. La clé A ne permettra pas à la porte de s'ouvrir. C'est pour cela que le système est asymétrique : les deux clés ont des rôles différents.

Principe des clés complémentaires : publiques et privées

L'une des utilisations les plus courantes est celle où l'une des deux clés est la clé publique (pub) : tout le monde peut obtenir sa valeur et l'utiliser pour chiffrer un message m à destination de la personne qui connaît l'autre clé qu'on nomme la clé privée (pri) :

1. Un émetteur chiffre le message en utilisant la clé publique de chiffrement. Il obtient alors un message mc_pub chiffré.
2. On envoie sur le réseau le message chiffré, indéchiffrable avec la clé publique.
3. Le destinataire récupère ce message chiffré et utilise sa clé privée pri pour déchiffrer mcpub et récupérer le message m originel.

Deux différentes majeures avec le cas symétrique :

• Une personne peut émettre sa clé publique et n'importe qui pourra s'en servir pour chiffrer des messages à destination de cette personne.
• Seule la personne connaissant sa clé privée pourra déchiffrer les messages qu'on lui envoie.

C'est beaucoup mieux : on peut envoyer des messages chiffrés à distance sans crainte d'être espionné (pourvu que trouver la clé privée soit bien un problème DIFFICILE).

Utilisation sur Internet ?

Nous allons pouvoir utiliser ce système pour envoyer des messages sécurisés vers un serveur distant.

1. Le serveur peut transmettre en clair la clé pub de chiffrement
2. Le client peut alors envoyer un message chiffré en utilisant cette clé pub.
3. Le serveur peut déchiffrer les messages reçus en utilisant sa clé privée pri qu'il doit garder secrète.
   

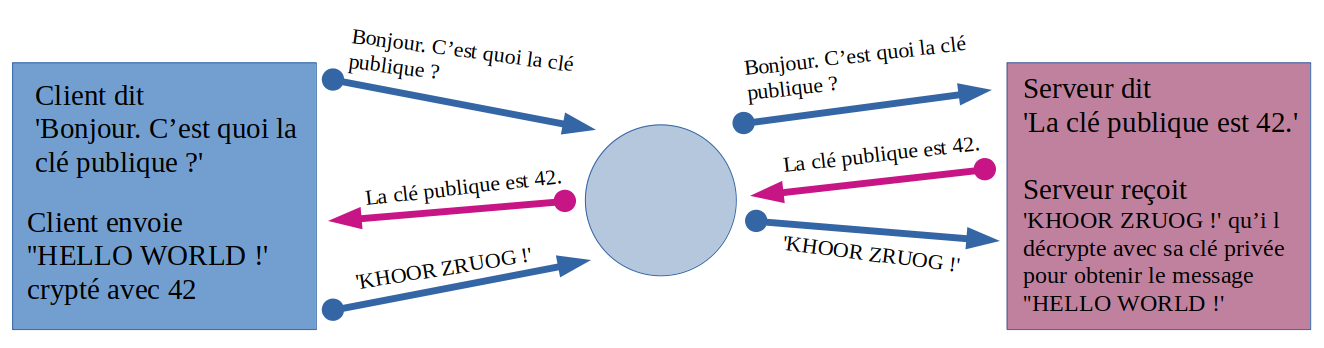
Même si quelqu'un écoute la conversion en espionnant le routeur du milieu, il ne pourra rien faire de la communication. A part savoir avec qui communique avec qui bien entendu.

Le problème vient néanmoins de la communication dans l'autre sens.

Le serveur pourrait chiffrer les messages qu'il veut envoyer à son client en utilisant sa clé privée pri. Mais comme il suffit d'utiliser la clé publique pub, connue de tous, pour déchiffrer les messages chiffrés avec pri, n'importe qui pourrait alors déchiffrer les messages..

Solution n°1 : tout le monde a son propre couple de clés (publique, privée)

Avec cette solution, le client génère également son propre couple de clés (pub2, pri2) et transmet sa propre clé pub2 publique au serveur. Il garde pour lui la clé privée.

Le serveur pourra alors lui envoyer des messages chiffrés que seul le client pourrait décoder. Simple et efficace, non ?

Et bien non. Cette technique de communication n'est pas celle qu'on utilise.

Deux raisons à cela :

1. Les méthodes asymétriques demandent beaucoup de temps de calcul, plus que les méthodes symétriques. Les communications de ce type sont donc viables uniquement sur des messages courts mais pas pour transférer des messages longs, comme des vidéos.
2. Cette communication ne protège pas contre les attaques du type Attaque de l'Homme du Milieu ou Man in The Middle en anglais.

L'homme du milieu, une technique qui met à mal la solution 1

Imaginons que Marie ait accès à l'un des routeurs se trouvant entre Alice et Bob(le serveur de la Banque ?).

Lorsqu'un message en clair pour Bob arrive sur le routeur, Marie en profite pour se faire passer pour Bob : elle transmet à Alice sa propre clé publique plutôt que celle de Bob...

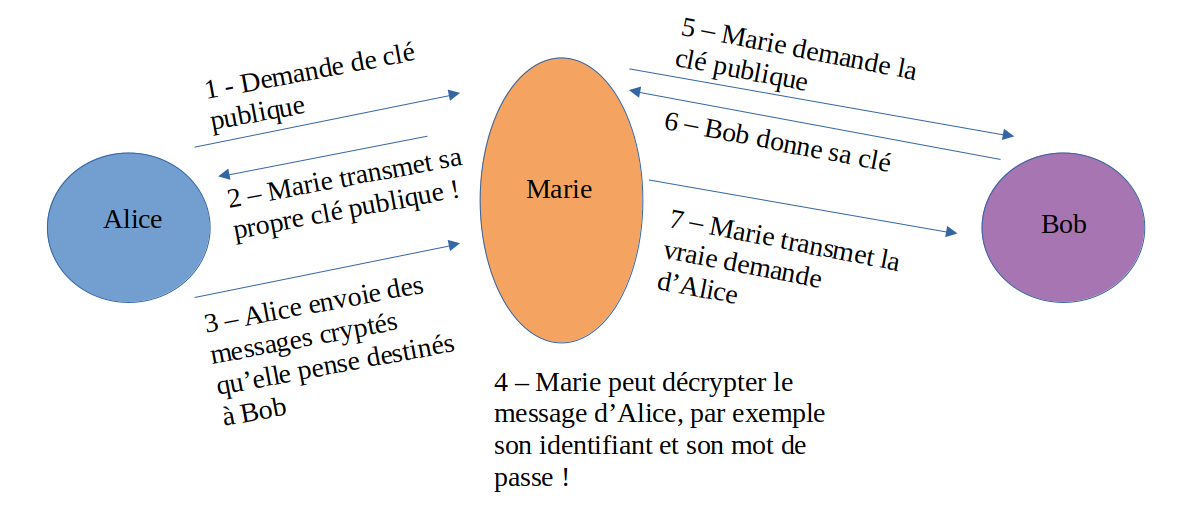
Ni Bob ni Alice ne se peuvent se rendre compte que quelque chose cloche : Marie parvient bien à se connecter à la banque et la banque a bien reçu les bons identifiants et mots de passe. La seule chose qui pourrait mettre la puce à l'oreil est un léger temps de latence puisque l'ordinateur de Marie doit déchiffrer puis chiffrer à nouveau les communications.

Solution 2 : utiliser le chiffrement symétrique pour transmettre une clé symétrique

Alice utilise la clé publique de Bob pour envoyer un message particulier : le message contient une clé SYMETRIQUE. Seul Bob peut déchiffrer le message et obtenir la clé sylétrique. Alice et Bob peuvent alors envouer l'un et l'autre des messages chiffrés en utilisant la clé symétrique qu'ils sont les seuls à connaître.

Notez par contre que si Marie se fait passer pour Bob dès le départ, ça ne change rien au problème de l'homme du milieu...

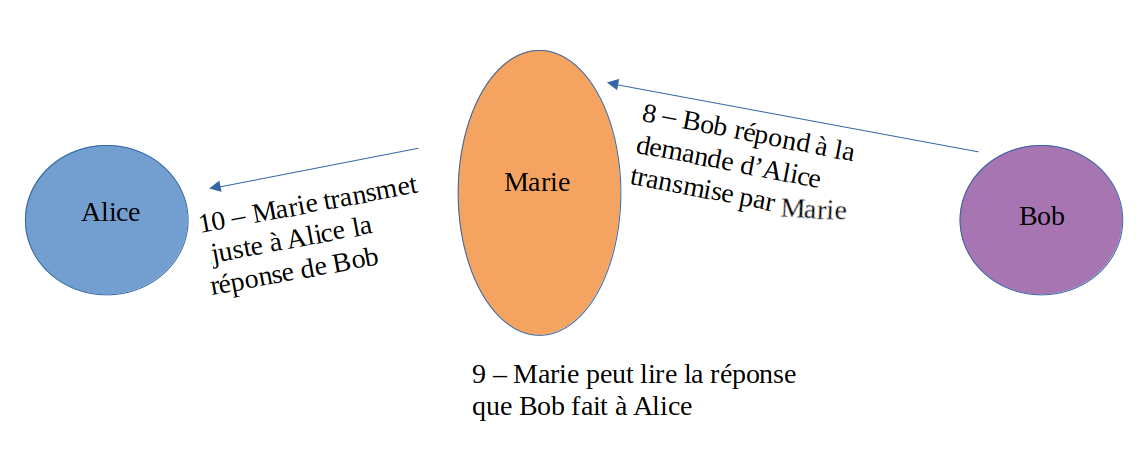
L'homme du milieu, une technique qui met à mal la solution 2

Si Marie récupère la communication initiale d'Alice lorsqu'elle demande la clé publique de Bob, cela ne change rien : Marie transmet sa propre clé publique et Alice va alors envoyer en toute confiance un message chiffré contenant la clé symétrique. Marie pourra déchiffrer le message avec sa clé privée et utilisera ensuite la clé symétrique pour continuer à se faire passer pour Bob.

Il a bien fallu créer une technique pour mettre à mal l'Homme du Milieu.

3 - Le tiers de confiance et les certificats d'authentification

⇩ ⇧ ⤊

Comment parvenir à identifier de façon certaine votre correspondant et éviter le problème de l'homme du milieu ?

Comment être certain que vous discutez bien avec votre Banque (B comme Banque ou Bob) par exemple ? En parlant argent, cela rend tout de suite les choses concrêtes !

L'une des solutions possibles est d'utiliser un tiers de confiance : un organisme reconnu et connu C (comme confiance ou Charlie...) par les deux ordinateurs cherchant à discuter.

Situation initiale : le tiers de confiance

On part du principe qu'Alice et Bob connaissent la clé pubC publique de C de façon certaine.

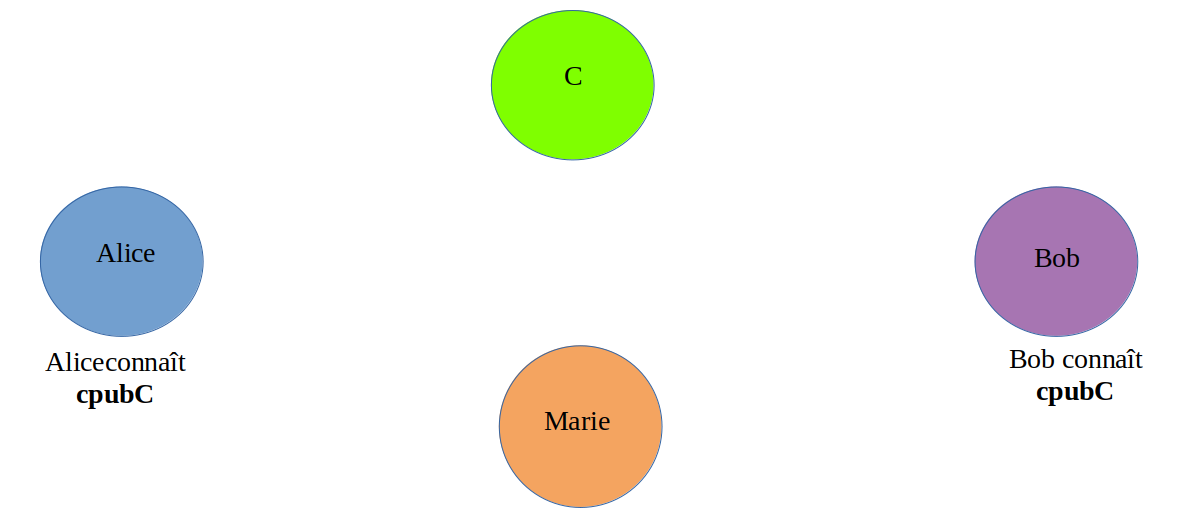
Comment est-ce possible sur vos ordinateurs ? Facile, vos ordinateurs et navigateurs Web intègrent de base les clés publiques des organismes reconnus tiers de confiance mondialement.

Nous allons voir que cette clé pubC ne va pas leur servir à chiffrer les messages de C mais à déchiffrer les messages que C à chiffrer avec sa clé privée priC.

Le serveur B demande son certificat de confiance

B communique avec C et transmet sa clé pubB.

L'organisme C va alors créer un certificat d'authentification permettant à A d'identifier B avec certitude (sous condition de faire confiance à C !).

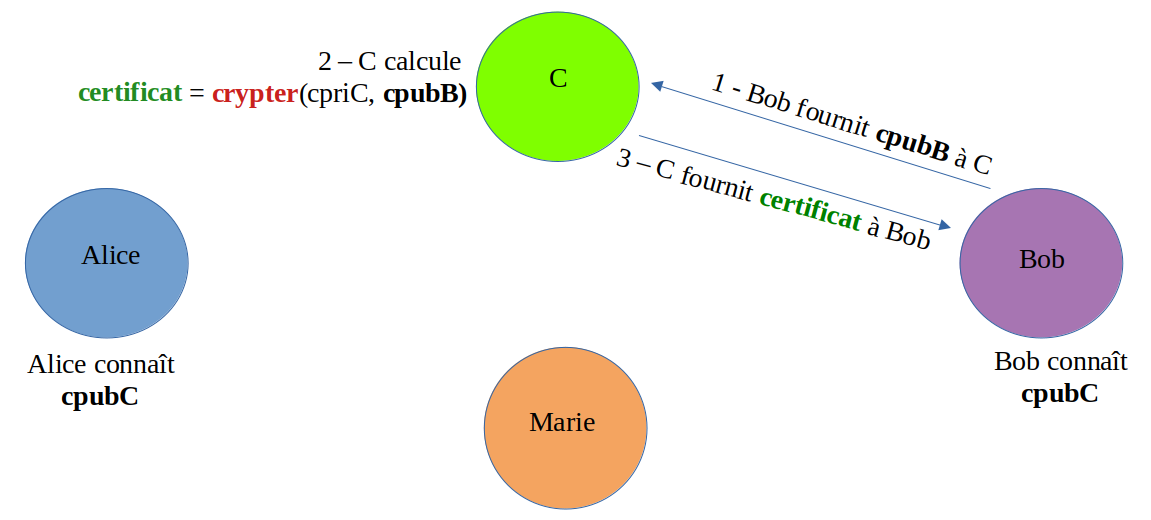
1. B fournit au moins à C sa clé pubB publique et son nom de domaine.
2. C va alors créer le certificat en chiffrant ces informations en utilisant sa clé privée priC puis
3. C fournit ce certificat d'authentification à Bob en retour

Puisque le certificat est un message chiffré avec la clé privée de C, on peut le déchiffrer pour lire son contenu en utilisant la clé publique de C. Cela tombe bien, tout le monde la connait.

Alice peut maintenant tenter de communiquer avec Bob

B peut maintenant prouver qu'il est bien B. Voilà comment.

4. A contacte B en clair pour obtenir sa clé publique
5. B transmet deux choses en clair : sa clé publique pubB et son certificat d'authentification par la même occasion : ni l'un ni l'autre ne sont des éléments à dissimuler.

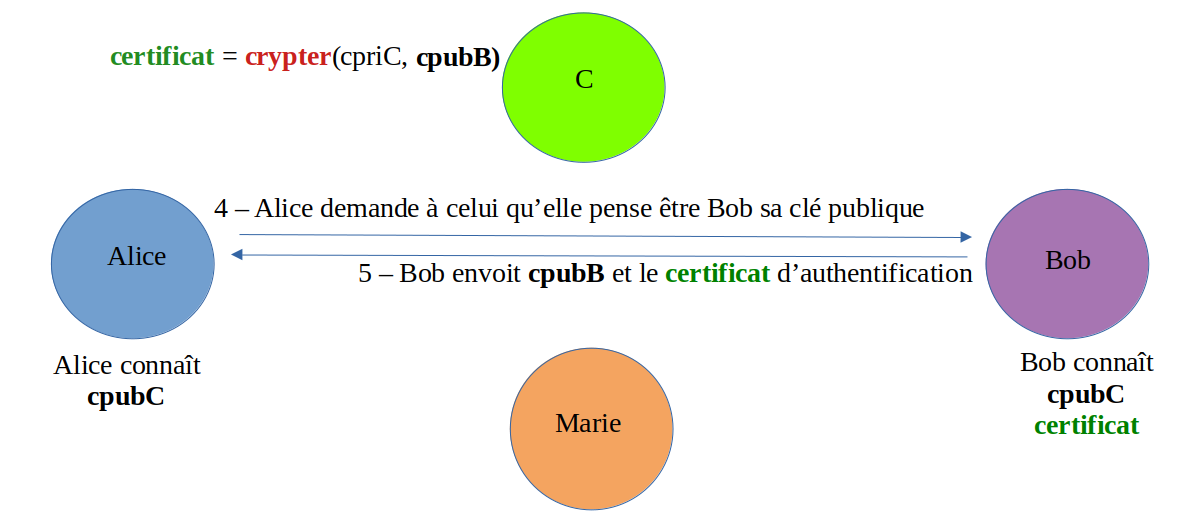
Maintenant qu'Alice a reçu une clé publique et un certificat d'authentification soit disant en provenance de B, que peut-elle en faire ?

Et bien, comme le certificat a été chiffré en utilisant la clé priC de C, elle peut le déchiffrer en utilisant la clé pubC de C. Cela tombe bien, elle la connaît et fait confiance en cette information.

Alice va donc calculer ceci :

dechiffrer(certificat, pubC) 

= dechiffrer(chiffrer("pubB et nom de domaine de B", priC), pubC) 

Il n'existe donc que trois possibilités :

• Soit le déchiffrement permet bien de récupérer le message contenant pubB et le nom de domaine de B : cela veut dire que le certificat provient bien de C (sinon l'utlisation de pubC n'aurait pas fonctionnée). Alice vient d'apprendre qu'elle parle bien à Bob.
• Soit le déchiffrement permet bien de récupérer le message contenant pubB et le nom de domaine de B MAIS cela ne correspond pas à la clé public que le soit-disant Bob lui a envoyé : cela veut dire que quelqu'un tente d'utiliser la technique de l'homme du milieu en fournissant le vrai certificat de Bob. Alice peut maintenant détecter la supercherie.
• Soit le déchiffrement ne donne aucun message cohérent. Cela veut dire que quelqu'un tente d'utiliser la technique de l'homme du milieu mais ne s'embête même pas à fournir un vrai certificat... Alice peut détecter la supercherie.

Cette fois, Marie ne peut plus jouer le rôle de Bob : elle ne peut pas envoyer ni le vrai certificat de Bob, ni un autre certificat... Il faudra qu'elle puisse créer un vrai certificat mais pour cela :

• Soit elle doit demander un C de lui fournir un certificat en disant qu'elle est B. Mais C étant une société serieuse, ça va demander un niveau d'escroquerie très important.
• Soit elle doit trouver la clé privée de C : un problème DIFFICILE. Si on lui laisse 300 ans, ça devrait donc être possible.

4 - HTTPS

⇩ ⇧ ⤊

Nous pouvons maintenant comprendre comment fonctionne une communication HTTPS qui est un mélange de chiffrement asymétrique (lors de l'authentification et l'établissement de la connection) puis de chiffrement symétrique (lors de la suite de la communication).

1. Un client dispose d'un navigateur Web disposant d'un ensemble de clés publiques correspondant aux organismes de certification auxquels les concepteurs du navigateur font confiance.
2. Un serveur se déclare auprès de l'un des organismes de certification et lui demande de lui fournir un certificat d'authentification.
3. Le client contacte le serveur en clair
4. Le serveur lui transmet en clair sa clé publique et son certificat
5. Le client vérifie la validité du certificat et de la clé publique
6. Le client utilise alors la clé publique du serveur authentifié pour discuter avec le serveur de la méthode de chiffrement symétrique qu'ils vont utiliser lors de cette session de communication : quel algorithme et quelle clé de chiffrement symétrique.
7. A partir de là, client et serveur peuvent communiquer de façon sécurisée en utilisant une méthode de chiffrement symétrique, moins gourmande en temps de calcul.

Et comment faire pour lire le certificat envoyé par un site ? Il suffit de cliquer sur le petit cadenas et de chercher ensuite dans les menus proposés par le navigateur.

A titre d'exemple, voici le début du certificat de ce site :

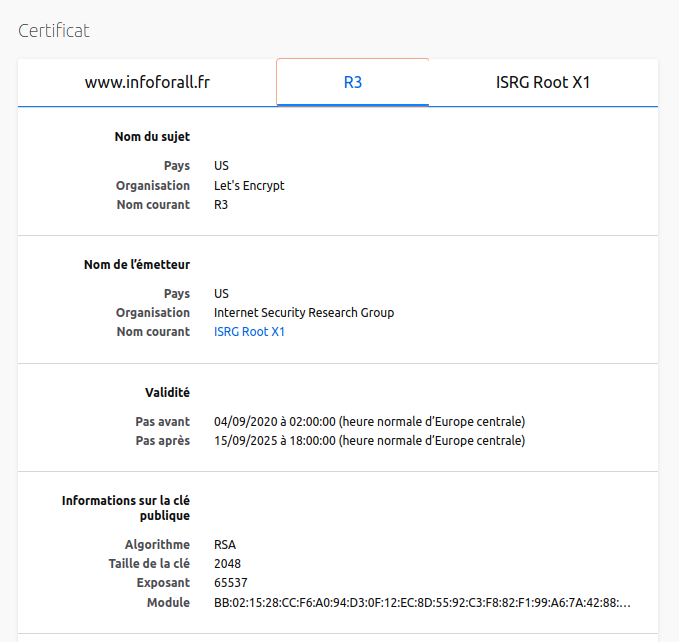
Le protocole HTTPS est en réalité constitué de deux protocoles :

1. Le protocole TTL (Transport Layer Security) est celui qui gère l'authentification via le certificat et le choix et l'établissement du protocole de chiffrement symétrique.
2. Une fois la communication établie, HTTPS utilise le protocole HTTP de façon habituelle si ce n'est que les requêtes et réponses HTTP sont chiffrées.

5 - FAQ

⇩ ⇧ ⤊

Des différences entre les autorités de certification