(Rappel) 1.1 Les tables de vérité
| Expression a | Expression b | a AND b | a NAND b | a OR b | a NOR b | a XOR b |
|---|---|---|---|---|---|---|
| FAUX | FAUX | FAUX | VRAI | FAUX | VRAI | FAUX |
| FAUX | VRAI | FAUX | VRAI | VRAI | FAUX | VRAI |
| VRAI | FAUX | FAUX | VRAI | VRAI | FAUX | VRAI |
| VRAI | VRAI | VRAI | FAUX | VRAI | FAUX | FAUX |
7 - Composition de portes logiques
Nouvelle version en cours
Nous avons vu comment réaliser des portes logiques avec des transistors.
On peut notamment faire des NON (NOT) et des NON-ET (NAND) avec des transistors.
Nous avons vu les opérations basiques ET (AND), OU (OR), NON-OU (NOR).
Voyons maintenant comment les associer pour réaliser des choses plus complexes.
Evaluation ✎ :
Documents de cours : open document ou pdf
1 - Rappel des symboles des portes logiques
(Rappel) 1.2 Symboles des portes logiques
On donne ici les symboles européens et américains ANSI.
| NOT |  |
|
| AND |  |
|
| NAND |  |
|
| OR |  |
|
| NOR |  |
|
| XOR |  |
(Rappel) 1.3 Système complet d'opérateurs
Système complet
Un ensemble donné d'opérateurs logiques est dit complet s'il permet de recréer tous les autres opérateurs logiques.
Voici quelques ensembles complets :
- {NOT, AND}
- {NOT, OR}
- {NAND}
- {NOR}
Exemple du {NOT, AND}
Les lois de De Morgan permettent facilement de montrer que ce système est complet.
- a NAND b = NOT (a AND b)
- a NOR b = NOT (a OR b) = NOT a AND NOT b
- a OR b = NOT (a NOR b) = NOT (NOT a AND NOT b)
2 - Egalité et différence
Nous allons travailler sur l'opérateur logique XOR et la façon dont on peut créer une porte logique XOR permettant de gérer un XOR bit à bit.
01° Compléter la table de vérité du XOR (en cliquant sur les cases de la sortie).
| Valeur de a | Valeur de b | a XOR b |
|---|---|---|
| 0 | 0 | ? |
| 0 | 1 | ? |
| 1 | 0 | ? |
| 1 | 1 | ? |
...CORRECTION...
| Valeur de a | Valeur de b | a XOR b |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
02° Utiliser la simulation ci-dessous pour expliquer pourquoi le XOR peut être utiliser en tant qu'opérateur de différence entre deux bits ?
...CORRECTION...
On obtient 1/VRAI en sortie uniquement si les deux bits d'entrée sont différents :
- 0 et 1
- 1 et 0
La porte répond bien VRAI uniquement sur cette différence.
03° Compléter le montage pour parvenir à créer un circuit détecteur de différence : il faudra X portes logiques XOR comparant chaque pair de bits puis associer leurs réponses pour obtenir la réponse finale.
...CORRECTION...
04° Lors de la question précédente, nous avons obtenu une porte logique DIFFERENCE, permettant de tester la différence entre deux entrées de X bits.
C'est l'équivalent Python de l'opérateur !=.
Modifier maintenant le schéma pour concevoir une porte logique EGALITE qui répondrait VRAI si les deux mots d'entrée sont EGAUX.
...CORRECTION...
Première possibilité
On remplace la porte OR de sortie pour une porte NOR qui va inverser le résultat final.
Deuxième possibilité
Rajouter un NON derrière le OU X bits. Cela revient à créer un NOR en réalité.
Troisième possibilité
Remplacer les XOR 2 bits par des XNOR 2 bits : il s'git des portes qui complémentent le XOR. Cette fois, ces portes sont à 1 en sortie su les deux bits sont identiques.
Il faut donc remplacer le OU X bits par un AND X bits pour signaler qu'il faut que toutes les réponses soient à 1 pour pouvoir répondre que les deux mots sont identiques.
Pour information : Symbole dans un schéma logique
On symbolise le XNOR comme un XOR complémenté.
3 - Composition de portes logiques
Si à partir d'un ensemble donné d'opérateurs (ou portes logiques), on peut créer toutes les autres portes possibles, on dit que cet ensemble de portes est complet. Définition similaire qu'avec les opérateurs logiques.
Technologie NAND
Dans l'activité sur la logique, nous avons vu que l'ensembles de opérateurs logiques {NOT, AND} permet de créer tous les autres opérateurs. Il en est de même évidemment avec l'ensembles des portes logiques {NOT, AND} qui permet de créer toutes les autres portes.
Nous allons maintenant voir qu'on peut récréer toutes les autres portes logiques en utilisant uniquement des portes NAND : l'ensemble de portes {NAND} est donc complet.
05° Utiliser le schéma suivant pour compléter sa table de vérité (en cliquant sur les cases de la table de vérité). En déduire la fonction logique que réalise ce montage.
| Bit d'entrée a | Bit de sortie s |
|---|---|
| 0 | ? |
| 1 | ? |
...CORRECTION...
Il s'agit de la table du NOT.
On peut donc réaliser un NOT à l'aide d'une porte NAND cablée de cette façon.
s = NOT a
06° Ecrire la formule réalisée par ce circuit. Pour cela, demandez vous ce que réalise chacun des NAND présents sur le schéma.
Utiliser ensuite le schéma interactif pour compléter sa table de vérité (en cliquant sur les cases de la table de vérité). En déduire la fonction logique calculée avec un schéma de ce type.
| Bit d'entrée a | Bit d'entrée b | Bit de sortie s |
|---|---|---|
| 0 | 0 | ? |
| 0 | 1 | ? |
| 1 | 0 | ? |
| 1 | 1 | ? |
...CORRECTION...
Le second NAND est un inverseur.
Il inverse la réponse du premier qui est un NAND classique.
La formule calculée est donc :
s = NOT (a NAND b)
Cette formule revient à calculer un AND.
| Bit d'entrée a | Bit d'entrée b | Bit de sortie s |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
07° Ecrire la formule réalisée par ce circuit. Pour cela, demandez vous ce que réalise chacun des NAND présents sur le schéma.
Utiliser ensuite le schéma interactif pour compléter sa table de vérité (en cliquant sur les cases de la table de vérité). En déduire la fonction logique calculée avec un schéma de ce type.
| Bit d'entrée a | Bit d'entrée b | Bit de sortie s |
|---|---|---|
| 0 | 0 | ? |
| 0 | 1 | ? |
| 1 | 0 | ? |
| 1 | 1 | ? |
...CORRECTION...
Les deux NAND de gauche sont des inverseurs.
Le NAND de droite est un NAND classique qui travaille sur les entrées (NOT a) et (NOT b).
La formule calculée est donc (les parenthèses ne sont pas obligatoires car NOT est prioritaire) :
s = (NOT a) NAND (NOT b)
Cette formule revient à calculer un OR.
| Bit d'entrée a | Bit d'entrée b | Bit de sortie s |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
08° Ecrire la formule réalisée par ce circuit. Pour cela, demandez vous ce que réalise chacun des NAND présents sur le schéma.
Utiliser ensuite le schéma interactif pour compléter sa table de vérité (en cliquant sur les cases de la table de vérité). En déduire la fonction logique calculée avec un schéma de ce type.
| Bit d'entrée a | Bit d'entrée b | Bit de sortie s |
|---|---|---|
| 0 | 0 | ? |
| 0 | 1 | ? |
| 1 | 0 | ? |
| 1 | 1 | ? |
...CORRECTION...
Réponse courte : il s'agit du circuit de la question précédente (le OR) mais on complémente la sortie.
Il s'agit donc d'un circuit permettant de réaliser un NOR.s = NOT( (NOT a) NAND (NOT b) )
| Bit d'entrée a | Bit d'entrée b | Bit de sortie s |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
09° Ecrire la formule réalisée par ce circuit. Pour cela, demandez vous ce que réalise chacun des NAND présents sur le schéma.
Utiliser ensuite le schéma interactif pour compléter sa table de vérité (en cliquant sur les cases de la table de vérité). En déduire la fonction logique calculée avec un schéma de ce type.
| Bit d'entrée a | Bit d'entrée b | Bit de sortie s |
|---|---|---|
| 0 | 0 | ? |
| 0 | 1 | ? |
| 1 | 0 | ? |
| 1 | 1 | ? |
...CORRECTION...
Trouver la formule est un peu plus compliqué que les fois précédentes.
Il faut commencer par voir que la première porte à gauche calcule s = a NAND b
La porte est en haut calcule donc s = a NAND (a NAND b)
La porte est en bas calcule donc s = b NAND (a NAND b)
La porte finale calcule donc s = (b NAND (a NAND b)) NAND (b NAND (a NAND b))
| Bit d'entrée a | Bit d'entrée b | Bit de sortie s |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Ce schéma correspond donc à une combinaison calculant a XOR b.
(Bilan, rien à connaître par coeur) 3.1 NOT avec des NAND
On peut construire un NOT en reliant les deux entrées d'une NAND
On a donc bien une réponse qui vaut NON a.
(Bilan, rien à connaître par coeur) 3.2 AND avec des NAND
Il suffit de prendre une NAND et de complémenter (inverser) le résultat.
a AND b = NOT (a NAND b)
Le premier NAND permet de réaliser une fonction NAND.
Le second NAND permet de réaliser une fonction NOT.
Avec des explications sur les schémas :
La sortie est NOT(a NAND b) = a AND b
(Bilan, rien à connaître par coeur) 3.3 OR avec des NAND
Comment faire un OR avec des NAND ?
Il faut :
- Inverser l'entrée a
- Inverser l'entrée b
- Appliquer NAND sur ces deux réponses
Les deux NAND de gauche permettent de réaliser une fonction NOT.
Le NAND de droite permette juste de réaliser une fonction NAND.
Avec quelques explications :
La sortie est donc NOT a NAND NOT b = a OR b
(Bilan, rien à connaître par coeur) 3.4 NOR avec des NAND
C'est facile : on prend le OU précédent est on le complémente !
La sortie est donc NOT( a OR b) = a NOR b
(Bilan, rien à connaître par coeur) 3.5 XOR avec des NAND
C'est plus complexe cette fois : il faut 4 NAND mais ils sont très imbriqués.
Avec quelques explications :
La sortie de la dernière NAND est donc (a NAND (a NAND b)) NAND ((a NAND b) NAND b) = a XOR b
(Bilan, rien à connaître par coeur) 3.6 XNOR avec des NAND
On prend le XOR précédent et on complémente.
L'activité Logique de la partie Algorithmique contient les démonstrations formelles des formules précédentes. Notez bien que puisqu'il n'y a que 4 cas à tester et qu'ils fonctionnent, les schémas interactifs sont une démonstration valide également. On parle de démonstration par cas.
Par contre, les schémas sont ici fournis ! Lorsqu'il a fallu les trouver, il a bien fallu établir la théorie et pas mettre les portes NAND au hasard.
Technologie NOR
On peut faire de même avec uniquement des portes NOR, ou des ensembles NOR et NOT.
Nous n'allons pas étudier les schémas ici, le principe est le même : on compense des assocations de NOR permettant de réaliser les bonnes fonctions.
Technologie Mixte
On peut également créer de nouvelles fonctionnalités en créant des circuits composés des opérateurs logiques de la théorie.
Ainsi, on peut réaliser une porte XOR en suivant précisement la formule logique du XOR :
a XOR b = (a AND NOT b) OR (NOT a AND b)
10° Réaliser un circuit XOR ayant deux entrées de 1 bit en combinant des portes NOT, AND et OR uniquement.
Votre circuit devra être compatible avec la table de vérité du XOR.
...CORRECTION...
4 - Addition
Commençons par regarder ce que donne la somme de a + b, a et b étant des nombres binaires.
(Rappel) 4.1 L'addition en binaire
| a | b | a + b |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 10 |
Séparons le résultat final sur deux colonnes : une pour la retenue éventuelle et une pour l'unité.
| a | b | Retenue de a + b | Unité de a + b |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
11° Répondre à ces trois questions :
- Quelle fonction logique correspond à la colonne de la retenue ?
- Quelle fonction logique correspond à la colonne de l'unité ?
- En déduire si l'additon est une action basique pour l'UAL, ou pas.
| a | b | Retenue de a + b | Unité de a + b |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
...CORRECTION...
| a | b | Retenue a AND b |
Unité a XOR b |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Pour réaliser une addition, il suffit d'un ET et d'un OU EXCLUSIF.
L'addition est donc bien une opération basique réalisable par l'UAL.
12° Réaliser un schéma comportant des portes logiques, comportant deux bits d'entrée a et b et qui calcule la retenue C et l'unité S obtenue lors du calcul binaire de a+b.
On nomme ce circuit capable uniquement d'additionner deux bits un demi-additionneur.
Vous devriez pouvoir vérifier les calculs basiques 0+0, 0+1, 1+0 et 1+1.
...CORRECTION...
Voir le bout de cours nommé demi-additionneur.
4.2 Demi-additionneur
Principe
Un circuit demi-additionneur permet de réaliser l'addition de deux bits sans gestion d'une éventuelle retenue déjà en mémoire.
- Il reçoit deux bits a et b en entrée
- Il fournit deux bits en sortie : l'unité S de la somme a+b et la retenue R à placer dans la colonne suivante.
Les résultats possibles en sortie sont donc :
- 0 + 0 = 0 : R = 0 et S = 0 si les deux entrées sont à 0;
- 0 + 1 = 0 : R = 0 et S = 1 si l'une des entrées est à 1;
- 1 + 1 = 10 : R = 1 et S = 0 si les deux entrées sont à 1.
Réalisation
On réalise la somme des deux bits et on obtient :
- L'unité S de la somme à l'aide de a XOR b;
- La retenue R provoquée par cette somme par a AND b.
Ainsi, si on additionne 1+1 en binaire, on obtient 10. Cela veut dire que l'unité est 0 et qu'il existe une retenue de 1.
Exemple interactif
Nous sommes maintenant faire le calcul de la première colonne lors de l'addition bit à bit. Mais si on passe à la deuxième colonne, on doit alors pouvoir faire l'addition des deux bits a et b de la nouvelle colonne et de l'éventuelle retenue R créée par l'addition dans la colonne précédente.
Il faut un disposif plus complexe qu'on nomme un additionneur.
4.3 Additionneur
Principe
Un circuit additionneur permet de réaliser l'addition de deux bits avec gestion d'une éventuelle retenue déjà en mémoire.
- Il reçoit trois bits en entrée : a, b de la nouvelle colonne et l'éventuelle retenue r_in / ringénérée lors du calcul sur la colonne précédente.
- Il fournit deux bits en sortie : l'unité S de la somme a+b+rin et la retenue R_out / Rout à placer dans la colonne suivante.
Les résultats possibles en sortie sont donc :
- 0 + 0 + 0 = 0 : Rout = 0 et S = 0 si les trois entrées sont à 0;
- 0 + 0 + 1 = 0 : Rout = 0 et S = 1 si l'une des entrées est à 1;
- 0 + 1 + 1 = 10 : Rout = 1 et S = 0 si les deux entrées sont à 1;
- 1 + 1 + 1 = 11 : Rout = 1 et S = 1 si les trois entrées sont à 1.
Construction de la solution en trois temps
Calcul de l'unité et la retenue de a+b
On commence par utiliser un demi-additionneur qui fournit l'unité S1 et la retenue R1 de la somme a+b.
C'est le circuit (XOR, AND) qui se trouve à gauche.
Calcul de l'unité de a + b + rin
On utilise alors un autre demi-additionneur qui prend en entrée l'unité S1 fournie le premier-demi-additionneur et la retenue rin d'entrée.
C'est le circuit (XOR, AND) qui se trouve au milieu.
L'unité S de la somme est bien calculée puisque S = (a XOR b) XOR rin donne bien 1 uniquement s'il y a un ou trois "1" parmi a, b, rin.
Calcul de la retenue de a + b + rin
Par contre, nous avons deux retenues.
- La retenue R1 vaut 1 si a et b sont à 1;
- La retenue R2 vaut 1 si R1 et rin sont à 1.
Ces deux cas sont disjoints (ils ne peuvent apparaître en même temps). Il suffit donc d'appliquer R1 OR R2 pour être certain de toujours mémoriser la bonne retenue finale Rout.
13° Finaliser le montage proposé pour en faire un additionneur.
...CORRECTION...
Voir le cours ci-dessous
4.4 Exemple interactif
14° Compléter le table de vérité suivant qui reprend l'exemple de l'addition. Vérifier que rin+a+b corresponde bien à l'ensemble des deux bits de sortie.
| rin | a | b | S1 = a XOR b | R1 = a AND b |
R2 = S1 AND rin |
Rout = R1 OR R2 |
S = S1 XOR rin |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | ? | ? | ? | ? | ? |
| 0 | 0 | 1 | ? | ? | ? | ? | ? |
| 0 | 1 | 0 | ? | ? | ? | ? | ? |
| 0 | 1 | 1 | ? | ? | ? | ? | ? |
| rin | a | b | S1 = a XOR b | R1 = a AND b |
R2 = S1 AND rin |
Rout = R1 OR R2 |
S = S1 XOR rin |
| 1 | 0 | 0 | ? | ? | ? | ? | ? |
| 1 | 0 | 1 | ? | ? | ? | ? | ? |
| 1 | 1 | 0 | ? | ? | ? | ? | ? |
| 1 | 1 | 1 | ? | ? | ? | ? | ? |
| rin | a | b | S1 = a XOR b | R1 = a AND b |
R2 = S1 AND rin |
Rout = R1 OR R2 |
S = S1 XOR rin |
...CORRECTION...
| rin | a | b | S1 = a XOR b | R1 = a AND b |
R2 = S1 AND rin |
Rout = R1 OR R2 |
S = S1 XOR rin |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
| rin | a | b | S1 = a XOR b | R1 = a AND b |
R2 = S1 AND rin |
Rout = R1 OR R2 |
S = S1 XOR rin |
5 - UAL X bits
Comment fait un ordinateur 8 bits pour réaliser l'addition de deux entrées de 8 bits ? Il utilise un ensemble de 8 additionneurs pour chacun des bits.
15° Utiliser ce montage comportant un additionneur 1 bit.
A quoi peut servir le bit de sortie qu'on trouve à gauche du montage ?
...CORRECTION...
La sortie de gauche est à 1 en cas de dépassement.
En plaçant deux bits d'entrée à 1, on constate que la sortie calculée est 0. Il y a bien dépassement : 1+1=0...
16° Compléter ce schéma pour parvenir à obtenir un additionneur 4 bits à partir de 4 additionneur 1 bit.
Réaliser quelques essais et tenter notamment d'obtenir un dépassement.
...CORRECTION...
17° Utiliser ce schéma qui intégre un additionneur 8 bits sous forme d'un simple symbole plutôt que sous la forme de 8 additionneurs 1 bit reliés entre eux.
Remarque : un seul symbole. Mais 8 additionneurs internes qui comportent chacun une porte XOR et une porte AND. Portes logiques qui sont elles-mêmes composées de plusieurs transistors.
Questions
- En combien d'étapes parvient-il à calculer la somme de deux entrées de 8 bits ?
- Combien d'étapes faudrait-il faire (et lesquelles) si on voulait l'utiliser pour réaliser la somme de deux entrées de 16 bits ?
...CORRECTION...
- Il fait la somme de deux entrées de 8 bits en une seule étape.
- Pour faire la somme de deux entrées de 16 bits, c'est plus compliqué pour lui :
- Chacune des deux donnée est stockée dans la RAM sous forme d'un bloc de 8 octets : A2 A1 et B2 B1 . On doit donc ramener quatre blocs de la RAM vers 4 registres de l'UAL. Assez lent mais on groupe la réception. Si l'UAL n'a pas assez de registres, il faudra donc effectuer le transfert voulu lors des étapes suivantes, ce qui va ralentir l'ensemble.
- On effectue l'addition A1 + B1 . On mémorise le résultat dans un registre C1 et on effectue A2 + B2 en rajoutant la retenue de l'addition précédente. On mémorise le résultat dans C2 .
- Le résultat final est formé des deux octets C2 C1 .
18° Quelques questions liées aux capacités de calcul des UAL (et du processeur qui les contient).
- Un processeur 16 bits (bus, mémoire, UAL, tout fonctionne avec 16 bits d'un coup) est-il meilleur qu'un processeur 8 bit pour traiter des données de 8 bits maximum ?
- Un processeur 16 bits (bus, mémoire, UAL, tout fonctionne avec 16 bits d'un coup) est-il meilleur qu'un processeur 8 bit pour traiter des données de 16 bits maximum ?
- On sait qu'on ne va travaillez qu'avec des données de 64 bits maximum. On vous propose un ordinateur double-coeur (2 processeurs) de 64 bits ou un ordinateur de 128 bits (1 processeur). Que choisir ? On considère que les deux ordinateurs ont la même fréquence de traitement.
- Vous ne travaillez qu'avec des données de 64 bits au maximum. On vous propose un ordinateur de 64 bits 3 Ghz ou un ordinateur de 128 bits 2 GHz. Que choisir ?
- Vous ne travaillez qu'avec des données de 128 bits au maximum. On vous propose un ordinateur de 64 bits 3 Ghz ou un ordinateur de 128 bits 2 GHz. Que choisir ?
...CORRECTION...
- Un processeur 16 bits (bus, mémoire, UAL, tout fonctionne avec 16 bits d'un coup) est-il meilleur qu'un processeur 8 bit pour traiter des données de 8 bits maximum ?
- Un processeur 16 bits (bus, mémoire, UAL, tout fonctionne avec 16 bits d'un coup) est-il meilleur qu'un processeur 8 bit pour traiter des données de 16 bits maximum ?
- On sait qu'on ne va travaillez qu'avec des données de 64 bits maximum. On vous propose un ordinateur double-coeur (2 processeurs) de 64 bits ou un ordinateur de 128 bits (1 processeur). Que choisir ? On considère que les deux ordinateur ont la même fréquence de traitement.
- Vous ne travaillez qu'avec des données de 64 bits maximum. On vous propose un ordinateur de 64 bits 3 Ghz ou un ordinateur de 128 bits 2 GHz. Que choisir ?
- Vous ne travaillez qu'avec des données de 128 bits au maximum. On vous propose un ordinateur de 64 bits 3 Ghz ou un ordinateur de 128 bits 2 GHz. Que choisir ?
Et bien non : dans les deux cas, chaque opération correspondra à une opération basique de l'UAL.
Cette fois, c'est oui car le processeur 16 bits utilisera toujours une seule opération sur chaque calcul. Le processeur 8 bits devra lui décomposer les opérations en plusieurs sous-opérations lorsqu'il devra traiter des données de plus de 8 bits. Il va donc être plus lent.
Cette fois, ça va dépendre du programme : est-il capable d'utiliser le double-coeur ou pas ?
Si le programme a été concu pour gèrer la capacité double-coeur, autant prendre le 64 bits.
Sinon, ça ne changera pas grande chose.
Comme les données sont sur 64 bits, la différence n'est pas sur le nombre de bits traitables en parallèle par le processeur.
Pour contre, l'ordinateur 64 bits traite 3 milliards d'opérations par seconde. Il est plus rapide que le 128 bits qui n'en traite que 2 milliards.
Cette fois, ça va dépendre du nombre de données réellement supérieures à 128 bits. Si elles sont nombreuses, autant partir sur l'ordinateur 128 bits, moins rapide mais n'effectuant les opérations sur les données de 128 bits en un cycle machine.
L'ordinateur de 64 bits est plus rapide (3 GHz) mais devra faire plusieurs sous-opérations pour les données de plus de 64 bits.
19° Voyons maintenant le schéma de l'UAL : un seul composant qui possède :
- deux entrées de données sur X bits (notées ici A et B);
- et une entrée de commande Op de 4 bits;
- une sortie S de X bits;
- et quelques autres entrées et sorties que nous n'allons pas étudier ici.
Questions
- Quel type de circuit active l'UAL lorsqu'on lui transmet une demande 0000 (ordre n°0) ?
- Quel type de circuit active l'UAL lorsqu'on lui transmet une demande 0001 (ordre n°1) ?
- Quel type de circuit active l'UAL lorsqu'on lui transmet une demande 0010 (ordre n°2) ?
- Quel type de circuit active l'UAL lorsqu'on lui transmet une demande 0011 (ordre n°3) ?
- Vérifier (par calcul direct de votre part) que 0100 (ordre n°4, -A) correspond à (256 - A) ici.
- Quel type de circuit active l'UAL lorsqu'on lui transmet une demande 1100 (ordre n°12) ?
...CORRECTION...
- 0000 : Addition des entrées, a + b.
- 0001 : Soustraction des entrées, a - b.
- 0010 : Successeur de a (a+1)
- 0011 : Prédecesseur de a (a-1)
- Cette formule correspond au complément à deux. Si vous ne l'avez pas encore vu, vous comprendrez son sens dans l'activité sur les nombres relatifs (les nombres positifs ou négatifs).
- 1100 : L'ordre 12 correspond au complémentaire de l'entrée.
6 - Si il reste du temps : multiplication et division
Nous avons vu que l'UAL peut réaliser :
- Des opérations logiques
- Des additions et des soustractions
On comprend bien qu'elle peut faire des multiplications puisque 5*10 n'est rien d'autres que 10+10+10+10+10. Puisqu'on peut réaliser une multiplication en faisant des additions, il est évident que l'UAL est capable de faire des multiplications.
Par contre, savez-vous pourquoi votre ordinateur multiplie très facilement par 2, 4, 8, 16, 32 ou 1024 alors qu'il mettra plus de temps pour d'autres nombres ?
Voici l'explication.
20° Utiliser l'UAL avec l'ordre 6 et 7 :
Questions
- Quelle opération est réalisée sous la commande Op = 6 ?
- En visualisant l'entrée A et la sortie S, expliquer comment l'ordinateur parvient facilement à réaliser cette opération.
- Quelle opération est réalisée sous la commande Op = 7 ?
- En visualisant l'entrée A et la sortie S, expliquer comment l'ordinateur parvient facilement à réaliser cette opération.
- Comment peut-on facilement réaliser la multiplication par 32 ?
...CORRECTION...
- Quelle opération est réalisée sous la commande Op = 6 ?
- En visualisant l'entrée A et la sortie S, expliquer comment l'ordinateur parvient facilement à réaliser cette opération.
- Quelle opération est réalisée sous la commande Op = 7 ?
- En visualisant l'entrée A et la sortie S, expliquer comment l'ordinateur parvient facilement à réaliser cette opération.
- Comment peut-on facilement réaliser la multiplication par 32 ?
La multiplication par 2.
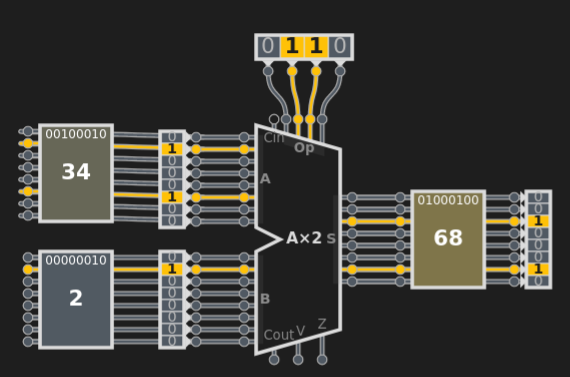
Décaler les bits vers la gauche a pour effet de multiplier les poids des cases par deux et donc de multiplier la valeur de l'entier par deux.
La division par 2.
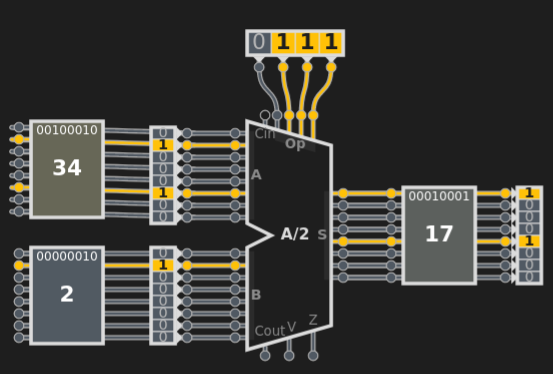
Décaler les bits vers la droite a pour effet de diviser les poids des cases par deux et donc de diviser la valeur de l'entier par deux.
2 = 21. Il faut donc décaler tous les bits de 1 position.
2 = 25. Il faut donc décaler tous les bits de 5 positions.
6.1 Multiplication d'un entier par 2N
Multiplication par un multiple de deux
Pour multiplier par 2N, l'UAL n'a qu'à décaler les bits de nombre entier de N cases vers la gauche.
X = 0000 0110 vaut 4+2=6 en décimal.
X*2 = 0000 1100 vaut 8+4=12 en décimal.
X*4 = 0001 1000 vaut 16+8=24 en décimal.
Division par un multiple de deux
Pour diviser par 2N, l'UAL n'a qu'à décaler les bits de nombre entier de N cases vers la droite.
X = 0110 0010 vaut 64+32+2= 98 en décimal.
X//2 = 0011 0001 vaut 32+16+1=49 en décimal.
X//4 = 0001 1000 vaut 16+8=24 en décimal.
Conclusion
La multiplication et division par une puissance de 2 n'étant qu'une affaire de décalage, l'UAL peut réaliser ces "calculs" précis très rapidement. Juste une histoire de décalage pour le circuit électronique.
Il y a donc interaction avec la partie Algorithmique : on cherchera toujours à privilégier les solutions utilisant de tels calculs car on sait qu'ils sont rapides à réaliser.
6.2 Possibilité de multiplication par un entier quelconque
Multiplication par un entier quelconque
L'une des façons de gérer la multiplication est de se rendre compte qu'on peut écrire le facteur multiplicateur en binaire.
Ainsi, si on doit effectuer k * 17, il faut se rendre compte que l'UAL ne "voit" pas 20 mais 16 et 4 :
17 = 0001 0100
Plutôt que de faire la multiplication M = k * 20, il suffit donc de réaliser des décalages et quelques additions.
- On obtient X1 en décalant k de 2 cases vers la gauche (pour multiplier par 4 = 22). Cette opération est rapide.
- On obtient X2 en décalant k de 4 cases vers la gauche (pour multiplier par 16 = 24). Cette opération est rapide.
- On obtient M en additionnant les bits de X1 et X2.
Exemple
M = k * n = 12 * 5
k = 12 = 00001100
n = 05 = 00000101
Pour réaliser la multiplication, il suffit donc de réaliser cette addition :
k 0 0 0 0 1 1 0 0
* n 0 0 0 0 0 1 0 1
--------------------------
- calcul via 2 additions -
--------------------------
0 0 0 0 1 1 0 0 (k * 1=20, pas de décalage)
+ 0 0 1 1 0 0 0 0 (k * 4=22, 2 décalages)
--------------------------
= 0 0 1 1 1 1 0 0
Voyons si cela fonctionne :
>>> 0b00111100
60
C'est bien le résultat attendu : 12 * 5 = 60.
6.3 Opérateurs de décalage binaire en Python
Python intègre deux opérateurs permettant de réaliser des décalages de bits.
Décalage à gauche
L'opérateur << permet de décaler à gauche (provoquant une multiplication sur les bits encodent un entier).
Sa signature est OCTET << DECALAGE
>>> bin(12)
'0b1100'
>>> 12 << 1
24
>>> bin(24)
'0b11000'
>>> 12 << 4
192
>>> bin(192)
'0b11000000'
Décalage à droite
Même principe pour le décalage à droite (la division euclidienne si les bits représentent un entier).
>>> bin(12)
'0b1100'
>>> 12 >> 1
6
>>> bin(6)
'0b110'
>>> 12 << 3
1
>>> bin(1)
'0b1'
Activité publiée le 07 03 2020
Dernière modification : 07 03 2020
Auteur : ows. h.