(Rappel) 1.1 TABLEAU : déclaration
A - Déclaration par extension
On déclare un tableau statique en utilisant un couple de crochets [...] en séparant les valeurs par des virgules.
Exemple avec un tableau d'entiers :
>>> notes = [20, 8, 18, 12]
>>> type(notes)
<class 'list'>
B - Déclaration d'un grand tableau
On peut déclarer un tableau sur plusieurs lignes en tapant sur ENTREE après chaque virgule. Exemple :
1
2
3
4
5
6
7 | eleves = ["Lisa",
"Scott",
"Matthias",
"Antoine",
"Ethan",
"Lucas",
"Manon"]
|
Cela prend plus de lignes mais on comprend un peu mieux ce qu'on place où par rapport à la version en une ligne :
1 | eleves = ["Lisa", "Scott", "Matthias", "Antoine", "Ethan", "Lucas", "Manon"]
|
C - Déclaration d'un tableau vide
Deux solutions : [] ou list().
>>> t = [] # solution 1
>>> t
[]
>>> t = list() # solution 2
>>> t
[]
>>> bool( [] )
False
(Rappel) 1.2 TABLEAU : accéder à une case avec [i]
Accès
On accéde à l'élément stocké dans la case d'indice i en utilisant des crochets : [i].
Indice 0 1 2 3
>>> notes = [20, 8, 18, 12]
>>> notes[0]
20
>>> notes[1]
8
>>> notes[2]
18
>>> notes[3]
12
>>> notes[4]
IndexError: list index out of range
Accès en lecture (list) : coût CONSTANT par rapport au nombre n d'éléments.
Trois choses à distinguer
- Le conteneur ⇨ t (le tableau)
- Les indices ⇨ i
- Les contenus ⇨ t[i]
(Rappel) 1.3 TABLEAU : déterminer sa longueur
La fonction native len() renvoie le nombre de cases du tableau :
Indice 0 1 2 3
>>> notes = [20, 8, 18, 12]
>>> len(notes)
4
4 notes donc des indices allant de 0 à 3.
Appel à len() sur un le type list : coût CONSTANT.
(Rappel) 1.4 TABLEAU : parcours par indice
On utilise une boucle for i in range(len(t)).
1
2
3
4 | # 0 1 2 3
t = [20, 8, 18, 12]
for i in range(len(t)): # Pour chaque indice possible dans t
print(t[i]) # Affiche le contenu de la case i
|
Le programme précédent est équivalent à ceci :
1
2
3
4
5
6 | t = [20, 8, 18, 12]
print(t[0])
print(t[1])
print(t[2])
print(t[3])
|
Ils affichent l'un et l'autre ceci dans la console :
20
8
18
12
- L4 : coût constant
- La boucle L3-L4 est réalisée n fois (autant que de cases).
- C'est donc LINÉAIRE : on réalise n fois une action constante.
2 - Matrice
En mathématiques, les matrices les plus simples sont des tableaux à deux dimensions contenant des nombres.
En informatique, les matrices sont des tableaux dont les éléments sont eux-mêmes des tableaux. Ce sont donc des tableaux de tableaux.
On peut remplir les tableaux avec autre chose que des nombres, mais au final on y stocke une information binaire, donc... un nombre.
Voici un plateau de jeu de 6 cases sur 6 cases comportant :
- Des couloirs (en blanc)
- Des murs (en noir)
- Des monstres (🐲)
- Le personnage du joueur (🧙 ou 🧚)
| Plateau de jeu | Colonne | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | ||
|---|---|---|---|---|---|---|---|
| Ligne | A | 0 | 0 | 0 | |||
| B | 0 | 🐲 | 0 | 0 | |||
| C | 0 | 🐲 | |||||
| D | 🧙 | 0 | 0 | ||||
| E | 0 | 0 | 0 | ||||
| F | 0 | 0 | |||||
Les petits dessins de cette page sont issus de l'UNICODE. Pour les utiliser sur une page HTML, il suffit de taper  où FFFFF correspond au code hexadécimal que vous aurez trouvé sur une page décrivant ces caractères.
On obtient 🧙 en tapant 🧹 dans le code HTML de la page.
On obtient 🧚 en tapant 🧚 dans le code HTML de la page.
On obtient 🐲 en tapant 🐲 dans le code HTML de la page.
Néanmoins, il faut faire attention : les caractères UNICODE ne sont pas toujours représentés exactement de la même façon sur les différents systèmes. A titre d'exemple, voici comment le plateau de jeu apparaît sur mon système qui lit exactement le même code HTML que le votre :
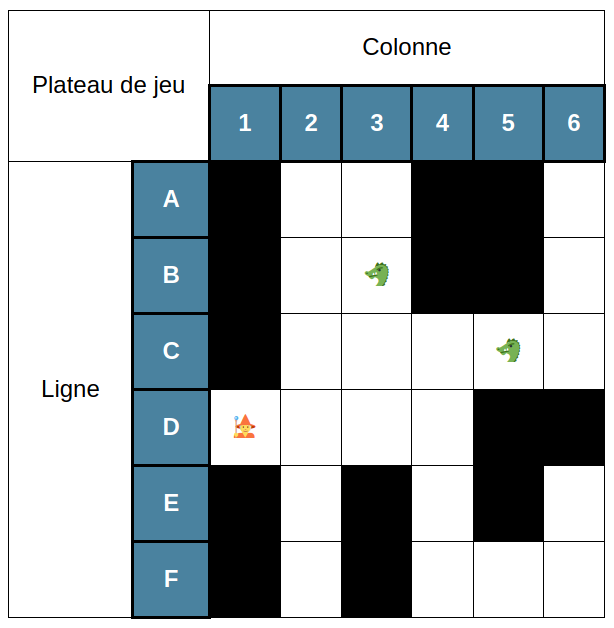
Comment faire pour encoder le contenu des cases ?
2.1 Méthode 1 : on utilise des nombres
On pourrait choisir d'encoder la présence :
- d'une case vide correspondant à un couloir par 0
- d'une case contenant un mur par 1
- d'une case contenant un monstre par 3
- de la case contenant le personnage du joueur par 8
Exemple visuel :
1 0 0 1 1 0
1 0 3 1 1 0
1 0 0 0 3 0
8 0 0 0 1 1
1 0 1 0 1 0
1 0 1 0 0 0
On représente notre plateau de jeu sous la forme d'un tableau à double entrée. Attention : le premier indice est 0, pas 1 !
| Plateau de jeu | Colonne | ||||||
| 0 | 1 | 2 | 3 | 4 | 5 | ||
|---|---|---|---|---|---|---|---|
| Ligne | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 3 | 1 | 1 | 0 | |
| 2 | 1 | 0 | 0 | 0 | 3 | 0 | |
| 3 | 8 | 0 | 0 | 0 | 1 | 1 | |
| 4 | 1 | 0 | 1 | 0 | 1 | 0 | |
| 5 | 1 | 0 | 1 | 0 | 0 | 0 | |
Pour rappel :

2.2 Méthode 2 : on utilise des caractères
On pourrait choisir d'encoder la présence :
- d'une case vide correspondant à un couloir par .
- d'une case contenant un mur par X
- d'une case contenant un monstre par m
- de la case contenant le personnage par o
Exemple visuel :
X . . X X .
X . m X X .
X . . . m .
o . . . X X
X . X . X .
X . X . . .
| Plateau de jeu | Colonne | ||||||
| 0 | 1 | 2 | 3 | 4 | 5 | ||
|---|---|---|---|---|---|---|---|
| Ligne | 0 | 'X' | '.' | '.' | 'X' | 'X' | '.' |
| 1 | 'X' | '.' | 'm' | 'X' | 'X' | '.' | |
| 2 | 'X' | '.' | '.' | '.' | 'm' | '.' | |
| 3 | 'o' | '.' | '.' | '.' | 'X' | 'X' | |
| 4 | 'X' | '.' | 'X' | '.' | 'X' | '.' | |
| 5 | 'X' | '.' | 'X' | '.' | '.' | '.' | |
Pour rappel :

Bref, il y autant d'encodages possibles du contenu des cases qu'on veut.
Question : comment peut-on parvenir à stocker un tableau à double entrée ?
3 - Création d'une matrice
Comment parvenir à encoder concrètement une matrice alors que nous avons rencontré uniquement des tableaux à une dimension pour l'instant ?
| Plateau de jeu | Colonne | ||||||
| 0 | 1 | 2 | 3 | 4 | 5 | ||
|---|---|---|---|---|---|---|---|
| Ligne | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 3 | 1 | 1 | 0 | |
| 2 | 1 | 0 | 0 | 0 | 3 | 0 | |
| 3 | 8 | 0 | 0 | 0 | 1 | 1 | |
| 4 | 1 | 0 | 1 | 0 | 1 | 0 | |
| 5 | 1 | 0 | 1 | 0 | 0 | 0 | |
La réponse est évidente : nous allons faire un tableau contenant... des tableaux.
Un tableau par ligne
Commençons par créer 6 tableaux, un tableau pour chaque ligne.
1
2
3
4
5
6
7
8 | ligne0 = [1, 0, 0, 1, 1, 0]
ligne1 = [1, 0, 3, 1, 1, 0]
ligne2 = [1, 0, 0, 0, 3, 0]
ligne3 = [8, 0, 0, 0, 1, 1]
ligne4 = [1, 0, 1, 0, 1, 0]
ligne5 = [1, 0, 1, 0, 0, 0]
print(ligne2[4])
|
01° Que va afficher ce programme ?
1
2
3
4
5
6
7
8 | ligne0 = [1, 0, 0, 1, 1, 0]
ligne1 = [1, 0, 3, 1, 1, 0]
ligne2 = [1, 0, 0, 0, 3, 0]
ligne3 = [8, 0, 0, 0, 1, 1]
ligne4 = [1, 0, 1, 0, 1, 0]
ligne5 = [1, 0, 1, 0, 0, 0]
print(ligne2[4])
|
...CORRECTION...
La ligne 8 indique d'aller chercher dans le tableau ligne2 l'élément d'indice 4.
3 | 0 1 2 3 4 5
ligne2 = [1, 0, 0, 0, 3, 0]
|
On afficher donc 3.
02° Que va afficher le programme si on remplace la ligne 8 par celle-ci ?
8 | print(ligne4[1])
|
...CORRECTION...
La ligne 8 indique d'aller chercher dans le tableau ligne4 l'élément d'indice 1.
5 | 0 1 2 3 4 5
ligne4 = [1, 0, 1, 0, 1, 0]
|
On affiche 0.
Voyons maintenant comment parvenir à encoder la matrice dans sa totalité.
Un tableau contenant les 6 tableaux
On crée un tableau matrice dont les éléments sont les tableaux-lignes précédents.
1
2
3
4
5
6
7
8
9
10 | ligne0 = [1, 0, 0, 1, 1, 0]
ligne1 = [1, 0, 3, 1, 1, 0]
ligne2 = [1, 0, 0, 0, 3, 0]
ligne3 = [8, 0, 0, 0, 1, 1]
ligne4 = [1, 0, 1, 0, 1, 0]
ligne5 = [1, 0, 1, 0, 0, 0]
mat = [ligne0, ligne1, ligne2, ligne3, ligne4, ligne5]
print(mat[2][4])
|
03° Que contient mat[2] ? Que contient mat[2][4] ?
1
2
3
4
5
6
7
8
9
10 | ligne0 = [1, 0, 0, 1, 1, 0]
ligne1 = [1, 0, 3, 1, 1, 0]
ligne2 = [1, 0, 0, 0, 3, 0]
ligne3 = [8, 0, 0, 0, 1, 1]
ligne4 = [1, 0, 1, 0, 1, 0]
ligne5 = [1, 0, 1, 0, 0, 0]
mat = [ligne0, ligne1, ligne2, ligne3, ligne4, ligne5]
print(mat[2][4])
|
...CORRECTION...
Contenu de mat[2] = ligne2 = [1, 0, 0, 0, 3, 0]
Contenu de mat[2][4] = [1, 0, 0, 0, 3, 0][4] = 3
04° Que contient mat[1] ? Que contient mat[1][0] ?
...CORRECTION...
Contenu de mat[1] = ligne1 = 1, 0, 3, 1, 1, 0]
Contenu de mat[1][0] = [1, 0, 3, 1, 1, 0][0] = 1
05° Que va-t-on récupérer si on tape mat[3] ? mat[3][0] ?
1
2
3
4
5
6
7
8 | mat = [
[1, 0, 0, 1, 1, 0],
[1, 0, 3, 1, 1, 0],
[1, 0, 0, 0, 3, 0],
[8, 0, 0, 0, 1, 1],
[1, 0, 1, 0, 1, 0],
[1, 0, 1, 0, 0, 0]
]
|
...CORRECTION...
Voici l'élément 3 0 :
1
2
3
4
5
6
7
8 | mat = [
[1, 0, 0, 1, 1, 0],
[1, 0, 3, 1, 1, 0],
[1, 0, 0, 0, 3, 0],
[8, 0, 0, 0, 1, 1],
[1, 0, 1, 0, 1, 0],
[1, 0, 1, 0, 0, 0]
]
|
3.1 Les matrices avec Python
Définition
En Python, il s'agit donc du type list[list].
Exemple
1
2
3
4
5
6
7
8 | mat = [
[1, 0, 0, 1, 1, 0],
[1, 0, 3, 1, 1, 0],
[1, 0, 0, 0, 3, 0],
[8, 0, 0, 0, 1, 1],
[1, 0, 1, 0, 1, 0],
[1, 0, 1, 0, 0, 0]
]
|
Accès aux cases
- Les éléments du tableau mat sont bien des tableaux-lignes encodant le contenu des lignes.
- mat[2] est ici surligné en jaune.
- mat[2][4] est ici en rouge.
1
2
3
4
5
6
7
8 | mat = [
[1, 0, 0, 1, 1, 0],
[1, 0, 3, 1, 1, 0],
[1, 0, 0, 0, 3, 0],
[8, 0, 0, 0, 1, 1],
[1, 0, 1, 0, 1, 0],
[1, 0, 1, 0, 0, 0]
]
|
Pour accéder à une case précise dans une matrice, il suffit donc de fournir d'abord son numéro de ligne puis son numéro de colonne.
Système de coordonnées
Avec le système de coordonnées ci-dessous :
mat[num_ligne][num_colonne] = mat[y][x]
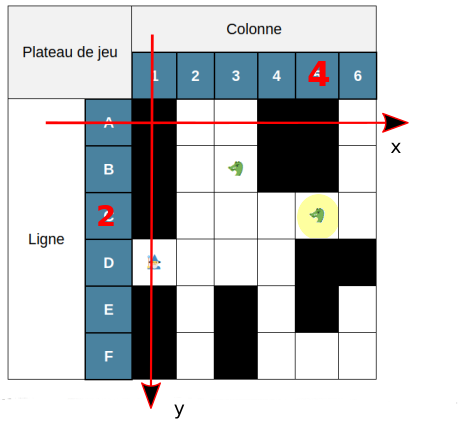
4 - Lecture et affichage
Pour parcourir toutes les cases d'une matrice, nous allons utiliser des boucles imbriquées :
Pour chaque ligne de la matrice
Pour chaque chaque colonne de la matrice
Agir en fonction des valeurs des lignes et colonnes
06-A° Voyons comment afficher une "ligne" à la fois avec un parcours par indice. Utiliser ce programme pour vous convaincre qu'il affiche les tableaux qui encodent le contenu des lignes de la matrice m.
1
2
3
4
5
6
7
8
9
10
11
12 | mat = [
[1, 0, 0, 1, 1, 0],
[1, 0, 3, 1, 1, 0],
[1, 0, 0, 0, 3, 0],
[8, 0, 0, 0, 1, 1],
[1, 0, 1, 0, 1, 0],
[1, 0, 1, 0, 0, 0]
]
for y in range(len(mat)): # Pour chaque numéro de lignes
print(mat[y])
|
[1, 0, 0, 1, 1, 0]
[1, 0, 3, 1, 1, 0]
[1, 0, 0, 0, 3, 0]
[8, 0, 0, 0, 1, 1]
[1, 0, 1, 0, 1, 0]
[1, 0, 1, 0, 0, 0]
Question
L'expression len(mat) correspond-t-elle au nombre de lignes ou au nombre de colonnes ?
...CORRECTION...
La matrice est un tableau de tableaux : ces éléments sont donc les tableaux qui contiennent les lignes.
La fonction len(mat) va donc vous ramener le nombre de lignes.
Pour vous en convaincre, il suffit d'écrire la matrice sous cette forme :
mat = [
[... les valeurs sur la ligne 0 ...]
[... les valeurs sur la ligne 1 ...]
[... les valeurs sur la ligne 2 ...]
[... les valeurs sur la ligne 3 ...]
[... les valeurs sur la ligne 4 ...]
[... les valeurs sur la ligne 5 ...]
]
06-B° Voyons comment afficher le contenu des cases une à une avec un double parcours par indice. Utiliser ce programme pour vous convaincre qu'il affiche les cases de la matrice m.
1
2
3
4
5
6
7
8
9
10
11
12
13 | mat = [
[1, 0, 0, 1, 1, 0],
[1, 0, 3, 1, 1, 0],
[1, 0, 0, 0, 3, 0],
[8, 0, 0, 0, 1, 1],
[1, 0, 1, 0, 1, 0],
[1, 0, 1, 0, 0, 0]
]
for y in range(len(mat)): # Pour chaque numéro de lignes y
for x in range(len(mat[0])): # Pour chaque numéro de colonnes x
print(mat[y][x])
|
1 # Correspond à mat[0][0], début du tableau
0 # Correspond à mat[0][1]
0 # Correspond à mat[0][2]
1 # Correspond à mat[0][3]
1 # Correspond à mat[0][4]
0 # Correspond à mat[0][5]
1 # Correspond à mat[1][0], début de la ligne suivante
0 # Correspond à mat[1][1]
3 # Correspond à mat[1][2]
1 # Correspond à mat[1][3]
...
Questions
Expliquer pourquoi len(mat[0]) correspond bien au nombre de colonnes.
L'expression len(mat[1]) donne-t-elle le même résultat ?
...CORRECTION...
len(mat[0]) va ramener le tableau surligné en jaune, qui correspond aux valeurs sur cette ligne.
Si on cherche sa "longueur", on va donc obtenir le nombre de colonnes sur la ligne.
1
2
3
4
5
6
7
8 | mat = [
[1, 0, 0, 1, 1, 0],
[1, 0, 3, 1, 1, 0],
[1, 0, 0, 0, 3, 0],
[8, 0, 0, 0, 1, 1],
[1, 0, 1, 0, 1, 0],
[1, 0, 1, 0, 0, 0]
]
|
len(mat[1]) va ramener exactement la même valeur puisque par définition, une matrice est un tableau de tableaux ayant tous le même nombre de cases.
06-C° Pour obtenir un affichage plus cohérent avec la notion de matrice, il faudrait ne pas passer à la ligne, sauf lorsqu'on a fini de donner les valeurs d'un des tableaux-lignes.
Pour cela, il faut modifier le comportement par défaut de print().
Action
Utiliser ce programme pour vous convaincre qu'il affiche bien mieux les cases de la matrice m.
1
2
3
4
5
6
7
8
9
10
11
12
13
14 | mat = [
[1, 0, 0, 1, 1, 0],
[1, 0, 3, 1, 1, 0],
[1, 0, 0, 0, 3, 0],
[8, 0, 0, 0, 1, 1],
[1, 0, 1, 0, 1, 0],
[1, 0, 1, 0, 0, 0]
]
for y in range(len(mat)): # Pour chaque numéro de lignes y
for x in range(len(mat[0])): # Pour chaque numéro de colonnes x
print(mat[y][x], end=" ")
print()
|
1 0 0 1 1 0
1 0 3 1 1 0
1 0 0 0 3 0
8 0 0 0 1 1
1 0 1 0 1 0
1 0 1 0 0 0
Questions
- Expliquer comment on parvient à ne pas changer systématiquement de ligne.
- Expliquer à quoi sert le print() qu'on réalise à chaque fois qu'on a terminé une boucle sur x (ligne 14).
...CORRECTION...
On ne change pas de lignes avec le print de la ligne 13 car on transmet un paramètre nommé end permettant de modifier le comportement en fin d'affichage. Ici, on lui dit de remplacer le passage à la ligne ("\n") par un simple espace (" ").
13 | print(mat[y][x], end=" ")
|
Le print() de la ligne 14 permet au contraire de forcer un passage à la ligne lorsqu'on a fini de noter les valeurs sur cette ligne : on transmet à un argument vide mais cela provoque le passage à la ligne par défaut.
06-D° On ne modifie pas les valeurs présentes dans la matrice. On peut donc utiliser des parcours par valeur plutôt que des parcours par indice.
Le code va paraître plus simple si les noms de variables sont bien choisies.
1
2
3
4
5
6
7
8
9
10
11
12
13
14 | mat = [
[1, 0, 0, 1, 1, 0],
[1, 0, 3, 1, 1, 0],
[1, 0, 0, 0, 3, 0],
[8, 0, 0, 0, 1, 1],
[1, 0, 1, 0, 1, 0],
[1, 0, 1, 0, 0, 0]
]
for ligne in mat: # Pour chaque tableau-ligne possible
for valeur in ligne: # Pour chaque valeur sur cette ligne
print(valeur, end=" ")
print()
|
1 0 0 1 1 0
1 0 3 1 1 0
1 0 0 0 3 0
8 0 0 0 1 1
1 0 1 0 1 0
1 0 1 0 0 0
Questions
- Comment sait-on qu'il s'agit d'un parcours par valeur ?
- Que contient ligne lors de la première boucle ?
- Que contient valeur lors de la première boucle ?
...CORRECTION...
- Derrière le in on place directement le nom du tableau : nous avons vu qu'on va récupérer directement les éléments du tableau.
- Lors du premier tour de boucle, ligne contient donc directement [1, 0, 0, 1, 1, 0].
- Lors du premier tour de boucle valeur contient alors le contenu de la case 0, c'est à dire l'entier 1 comme on peut le voir ci-dessus.
Parcours par valeur :
12 | for valeur in ligne:
|
Pour rappel, voici le parcours par indice :
12 | for x in range(len(mat[0])): # Pour chaque numéro de colonnes x
|
Maintenant que vous avez vu comment cela fonctionne, vous allez pouvoir tenter de retrouver cela vous même.
07-A° Compléter ce programme pour parvenir à afficher correctement la matrice en utilisant deux parcours par indice depuis la fonction afficher() qui reçoit dans son paramètre plateau la matrice qu'on veut afficher.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 | mat = [
[1, 0, 0, 1, 1, 0],
[1, 0, 3, 1, 1, 0],
[1, 0, 0, 0, 3, 0],
[8, 0, 0, 0, 1, 1],
[1, 0, 1, 0, 1, 0],
[1, 0, 1, 0, 0, 0]
]
def afficher(plateau:'list[list]') -> None:
"""Affiche le plateau dans la console"""
for y in ...: # Pour chaque numéro de lignes y
for x in ...
print(plateau[...][...], end=" ")
afficher(mat)
|
...CORRECTION...
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 | mat = [
[1, 0, 0, 1, 1, 0],
[1, 0, 3, 1, 1, 0],
[1, 0, 0, 0, 3, 0],
[8, 0, 0, 0, 1, 1],
[1, 0, 1, 0, 1, 0],
[1, 0, 1, 0, 0, 0]
]
def afficher(plateau:'list[list]') -> None:
"""Affiche le plateau dans la console"""
for y in range(len(plateau)): # Pour chaque numéro de lignes y
for x in range(len(plateau[0])): # Pour chaque numéro de colonnes x
print(plateau[y][x], end=" ")
afficher(mat)
|
07-B° Modifier le code pour parvenir à afficher correctement la matrice en utilisant deux parcours par valeur.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 | mat = [
[1, 0, 0, 1, 1, 0],
[1, 0, 3, 1, 1, 0],
[1, 0, 0, 0, 3, 0],
[8, 0, 0, 0, 1, 1],
[1, 0, 1, 0, 1, 0],
[1, 0, 1, 0, 0, 0]
]
def afficher(plateau:'list[list]') -> None:
"""Affiche le plateau dans la console"""
for ligne in ...: # Pour chaque ligne
for valeur in ...: # Pour chaque valeur sur cette ligne
print(..., end=" ")
afficher(mat)
|
...CORRECTION...
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 | mat = [
[1, 0, 0, 1, 1, 0],
[1, 0, 3, 1, 1, 0],
[1, 0, 0, 0, 3, 0],
[8, 0, 0, 0, 1, 1],
[1, 0, 1, 0, 1, 0],
[1, 0, 1, 0, 0, 0]
]
def afficher(plateau:'list[list]') -> None:
"""Affiche le plateau dans la console"""
for ligne in mat: # Pour chaque ligne
for valeur in ligne: # Pour chaque valeur sur cette ligne
print(valeur, end=" ")
afficher(mat)
|
Reste qu'afficher des numéros sur la console, c'est pas top. Passons à un vrai affichage.
4.2 Fonctions chr() ord()
UNICODE
Lien vers UNICODE.
Fonction native ord()
La fonction native ord() renvoie la valeur unicode du caractère fourni en argument.
ord(caractere:str) -> int
>>> ord('A')
65
>>> ord('B')
66
>>> ord('a')
97
>>> ord('z')
122
>>> ord('ç')
231
Fonction native chr()
La fonction native chr() renvoie le caractère de la valeur unicode fournie en argument.
chr(code:int) -> str
>>> chr(65)
'A'
>>> chr(231)
'ç'
>>> chr(9821)
'♝'
>>> chr(9822)
'♞'
>>> chr(9823)
'♟'
08° Chercher les caractères associés aux valeurs suivantes à l'aide la fonction native chr :
- 67
- 9760
- 9786
- 11035
...CORRECTION...
>>> chr(67)
'C'
>>> chr(9760)
'☠'
>>> chr(9786)
'☺'
>>> chr(11035)
'■'
UNICODE et affichage dans une console Python
Pour voir les caractères disponibles, allez sur cette page de Wikipedia : les UNICODE - les caractères.
Vous devriez trouver votre bonheur dans ces caractères, même si le choix est un peu plus limité. Attention néanmoins, les valeurs sont données en hexadécimal. N'oubliez pas de mettre Ox devant.
Dans la console Python, l'affichage des caractères UNICODE ne fonctionne souvent pas au delà de 65535 dans les implémentations actuelles de Thonny. Si vous demandez l'affichage d'un mage, ça ne fonctionnera pas malheureusement.
Par exemple, la page des pièces d'échec : ECHEC
09° Vous avez ci-dessous un nouveau programme utilisant une variable globale mat pour modéliser le plateau de jeu.
Deux différences principales par rapport aux programmes précédents :
- on lance (en ligne 26) un appel à la fonction afficher_plateau(). En ligne 11, on voit qu'elle stocke dans un paramètre plateau la matrice qu'on désire afficher
- cette fonction afficher_plateau() fait à son tour appel à la fonction afficher_case() qui reçoit l'entier modélisant la case et qui se charge de renvoyer le caractère qu'on veut voir à l'écran. Par exemple :
- Le personne (☺) plutôt que le code 8
- Le monstre (☠) plutôt que le code 3
- Un mur (■) plutôt que le code 1
- Pour le reste, un espace.
Le programme à compléter
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26mat = [ [1, 0, 0, 1, 1, 0], [1, 0, 3, 1, 1, 0], [1, 0, 0, 0, 3, 0], [8, 0, 0, 0, 1, 1], [1, 0, 1, 0, 1, 0], [1, 0, 1, 0, 0, 0] ] def afficher_plateau(plateau:'list[list]') -> None: """Affiche le plateau dans la console""" for y in range(len(plateau)): # Pour chaque numéro y de lignes for x in range(len(plateau[0])): # Pour chaque numéro x de colonnes caractere = afficher_case(plateau[y][x]) print(caractere, end=" ") print() def afficher_case(code:int) -> str: """Renvoie le caractère à afficher en fonction du code de la case""" return ' ' afficher_plateau(mat)Travail à réaliser
Compléter la fonction afficher_case() pour qu'elle réponde aux attendus de la documentation fournie.
L'appel ci-dessous dans la console devrait produire ceci :
■ ■ ■ ■ ☠ ■ ■ ■ ☠ ☺ ■ ■ ■ ■ ■ ■ ■
11
.
26 | def afficher_plateau(plateau:'list[list]') -> None: # DEFINITION
afficher(mat) # APPEL
|
...CORRECTION...
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33 | mat = [
[1, 0, 0, 1, 1, 0],
[1, 0, 3, 1, 1, 0],
[1, 0, 0, 0, 3, 0],
[8, 0, 0, 0, 1, 1],
[1, 0, 1, 0, 1, 0],
[1, 0, 1, 0, 0, 0]
]
def afficher_plateau(plateau:'list[list]') -> None:
"""Affiche le plateau dans la console"""
for y in range(len(plateau)): # Pour chaque numéro y de lignes
for x in range(len(plateau[0])): # Pour chaque numéro x de colonnes
caractere = afficher_case(plateau[y][x])
print(caractere, end=" ")
print()
def afficher_case(code:int) -> str:
"""Renvoie le caractère à afficher en fonction du code de la case"""
if code == 8 :
return chr(9786)
elif code == 3 :
return chr(9760)
elif code == 1 :
return chr(11035)
else :
return ' '
afficher_plateau(mat)
|
[BILAN] 4.2 Affichage d'une matrice sur la console
Principe
- Nombre de lignes : len(mat)
- Nombre de colonnes : len(mat[0])
Avec un parcours par indice
1
2
3
4
5
6
7
8
9
10
11
12
13
14 | mat = [
[1, 0, 0, 1, 1, 0],
[1, 0, 3, 1, 1, 0],
[1, 0, 0, 0, 3, 0],
[8, 0, 0, 0, 1, 1],
[1, 0, 1, 0, 1, 0],
[1, 0, 1, 0, 0, 0]
]
for y in range(len(mat)): # Pour chaque nnuméro de lignes y
for x in range(len(mat[0])): # Pour chaque numéro de colonnes x
print(mat[y][x], end=" ")
print()
|
Avec un parcours par valeur
1
2
3
4
5
6
7
8
9
10
11
12
13
14 | mat = [
[1, 0, 0, 1, 1, 0],
[1, 0, 3, 1, 1, 0],
[1, 0, 0, 0, 3, 0],
[8, 0, 0, 0, 1, 1],
[1, 0, 1, 0, 1, 0],
[1, 0, 1, 0, 0, 0]
]
for ligne in mat: # Pour chaque tableau-ligne possible
for valeur in ligne: # Pour chaque valeur sur cette ligne
print(valeur, end=" ")
print()
|
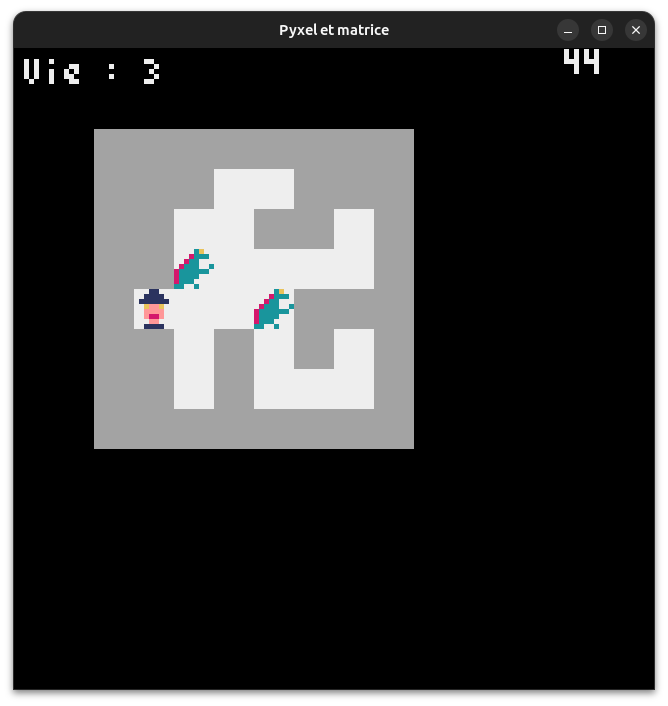
5 - Matrice avec Pyxel
Nous allons revoir une application Pyxel.
(Rappel) 5.1 Principe général d'un programme pyxel

Principe général
1 - init() crée la fenêtre graphique. Il faut lui fournir la largeur et la hauteur en pixels (ici 128 et 128) ;
- | |
2 - run() lance automatiquement 30 fois par seconde deux fonctions qui ont chacune un rôle précis :
- controler() récupère les événéments (clavier, souris...) et modifie les données ;
- afficher() efface l'ancienne image et en crée une nouvelle (frame en anglais).
- | |
Structure du code
1
2
3
4
5
6
7
8
9
10
11
12
13 | |
Système d'axes
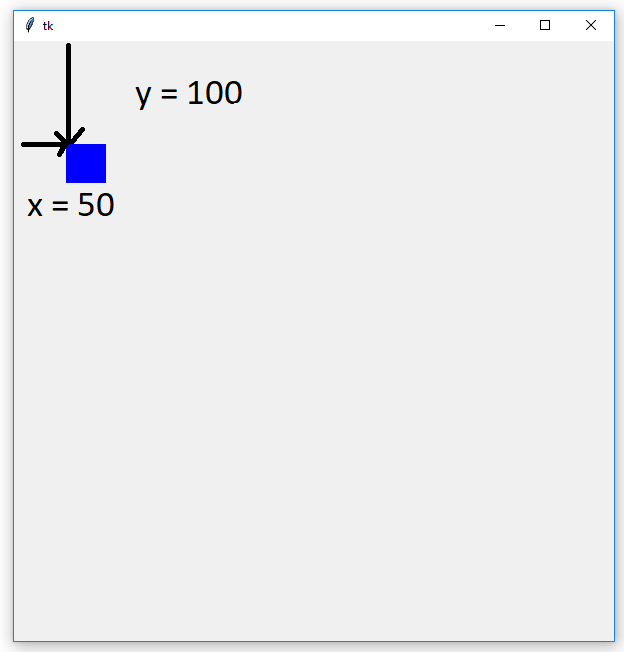
Le point (0,0) correspond au bord en haut à gauche.
L'axe Ox (abscisse) est orienté à droite : si x augmente, on va à droite.
L'axe Oy (abscisse) est orienté vers le bas, attention : si y augmente, on descend.
.
Notez bien que "tomber" veut donc dire qu'on augmente y avec ce système de coordonnées.
Fonction cls() et les couleurs
Important
Ici, nous allons avoir plusieurs coordonnées différentes :
- Les coordonnées x y dans la matrice qui correspondent aux numéros de colonnes et de lignes ;
- Les coordonnées x y dans la fenêtre graphique qui correspondent aux pixels de l'écran.
Pour éviter toute confusion, et puisque la documentation du module désigne par xy les coordonnées en pixels à l'écran, nous allons donc leur donner des noms différents :
- Les coordonnées dans la matrice : nC nL pour numéros de lignes et de colonnes ;
- Les coordonnées dans la fenêtre graphique : x y. Ce sont donc des valeurs en pixels.
10° Voici un premier programme pyxel permettant d'afficher notre plateau de jeu.
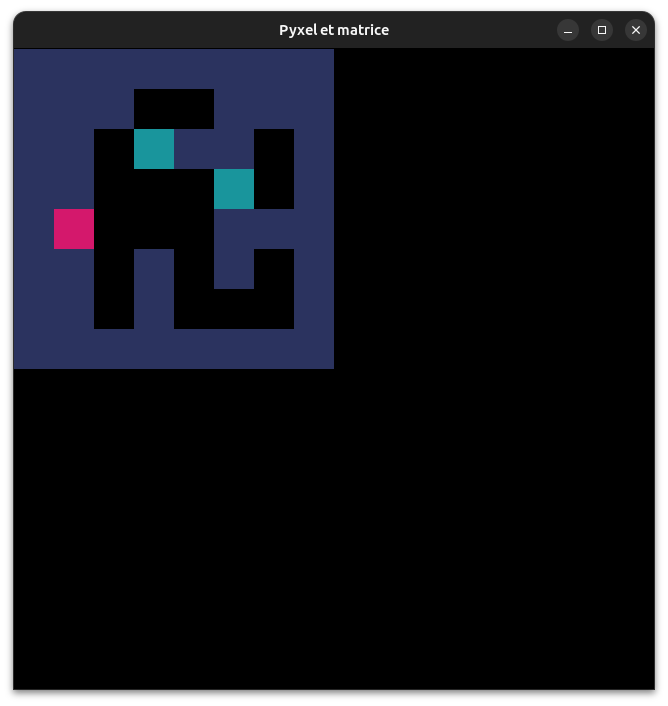
Notez que la matrice fournie est plus grande que le plateau de base du magicien : le fait d'entourer le plateau d'une muraille de 1 va nous permettre d'obtenir un code plus facile à gérer : nous n'aurons pas besoin de vérifier que la case où on désire se rendre existe puisqu'on ne peut pas sortir du cadre !
Lancez ce programme pour vérifier qu'il fonctionne puis répondre aux questions.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42 | |
Voici la structure des appels de fonctions :
Questions
- Dans quelle fonction (et sur quelle ligne) demande-t-on d'effacer l'écran ? Quelle est la couleur d'effacement ?
- On rappelle que la fonction rect() permet d'afficher un rectangle (lire le rappel ci-dessous au besoin). Traduire en français ce qu'on demande en ligne 36.
def rect(x:int, y:int, w:int, h:int, col:int) -> None
Dessine un rectangle de largeur w, de hauteur h et de couleur col dont les coordonnées en pixels du coin en haut à gauche sont x, y.
...CORRECTION...
- L'effacement avec cls(0) se trouve en ligne 26 dans la fonction afficher(). En allant voir la note 5.1 Principe général d'un programme pyxel, vous pourrez voir que c'est la couleur noire.
- En ligne 36, on fournit les coordonnées x et y du coin en haut à gauche de chaque carré. On multiplie par 8 les coordonnées nC et NL pour que les carrés ne se chevauchent pas. Les deux 8 suivants correspondent à la taille de la forme "8*8" et le dernier argument est le code dans cette case : on s'en sert pour définir la couleur du carré.
36 | |
Si le transfert argument vers paramètre n'est pas clair, voici une explication (optionnelle) plus longue :
Prototype de la fonction :
def rect(x:int, y:int, w:int, h:int, col:int) -> None
Appel de la fonction :
pyxel.rect(nC*8, nL*8, 8, 8, code_dans_la_case)
Il suffit de comparer l'ordre des arguments envoyés en ligne 36 :
- On envoie l'argument x*8 dans le paramètre local x ;
- On envoie l'argument y*8 dans le paramètre local y ;
- On envoie 8 dans w pour indiquer qu'on veut une forme de 8 pixels de large.
- On envoie 8 dans h pour indiquer qu'on veut une forme de 8 pixels de haut.
- On envoie code_dans_la_case dans col pour indiquer qu'on veut une forme de 8 pixels de haut.
Pourquoi multiplier par 8 ? Car on donne les coordonnées du coin en haut à gauche de chaque carré. On doit donc décaler de 8 pixels pour que les carrés ne se chevauchent pas.
11° Utiliser le code de la case (0, 1, 3 ou 8) en tant que couleur n'est pas top. Ce n'est pas très harmonieux et cela ne ressemble pas aux couleurs du personnage (bleu) et des monstres (vert).
Nous allons créer une nouvelle fonction nommée afficher_case() qui devra vous permettre d'afficher cela (sans modifier les codes dans la matrice !) :
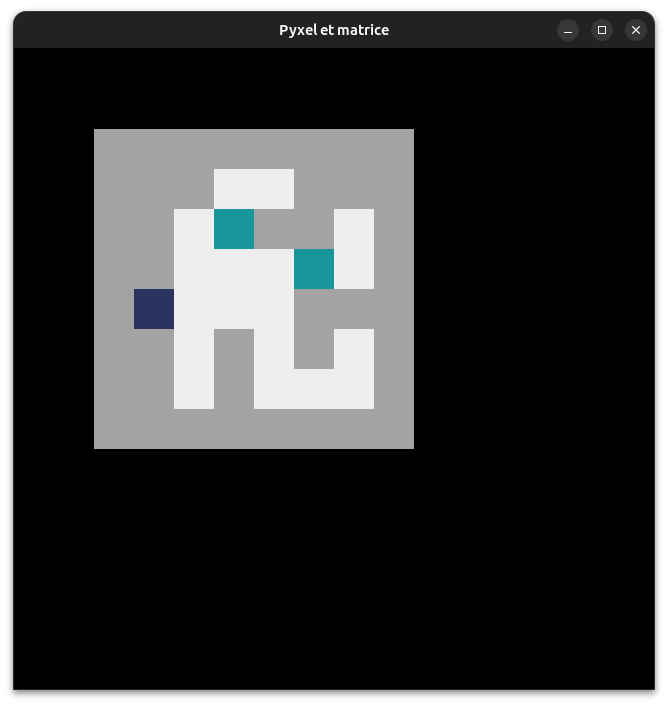
Elle reçoit les numéros nC et nL et sera chargée d'afficher le carré au bon endroit à l'écran. Et nous en profiterons pour lui demander de choisir une couleur en fonction du code lu plutôt que de prendre directement le code lu.
De la même façon, plutôt que de simplement multiplier les numéros par 8, nous pourrons effectuer une petite translation des cases pour qu'elles s'affichent un peu plus à droite et un peu plus vers le bas.
Rappel :

Compléter la nouvelle fonction pour qu'elle fasse correctement son travail.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65 | |
...CORRECTION...
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65 | |
6 - Matrice et pyxel edit
12-A° TRES IMPORTANT : ouvrir l'explorateur de fichiers et vérifiez que l'option "Affichage des extensions de fichiers" est bien activée.
L'affichage reste un peu décevant pour le moment : ce sont juste des carrés.
Voyons comment afficher de vraies choses.
- Sous Thonny : allez dans OPTIONS puis OUVRIR LA CONSOLE du système. Tapez ensuite pyxel edit res.pyxres
- Sous Pyxel Studio : cliquez simplement sur l'icône avec un PINCEAU ;
Cela devrait ouvrir le PYXEL_EDITOR qui va nous permettre de facilement dessiner en pixel art.
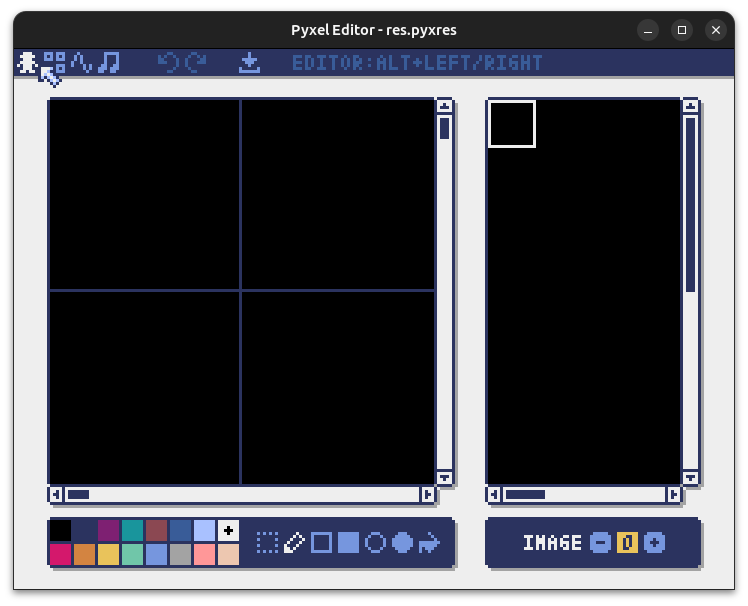
Dessiner puis sauvegarder à l'aide du bouton sous la flèche sur l'image ci-dessous, votre personnage et vos monstres. Pas la peine de faire comme ci-dessous, vous pouvez faire ce que vous voulez. Par contre, respectez bien les coordonnées : le magicien dans le carré en haut à gauche et le monstre juste en dessous.
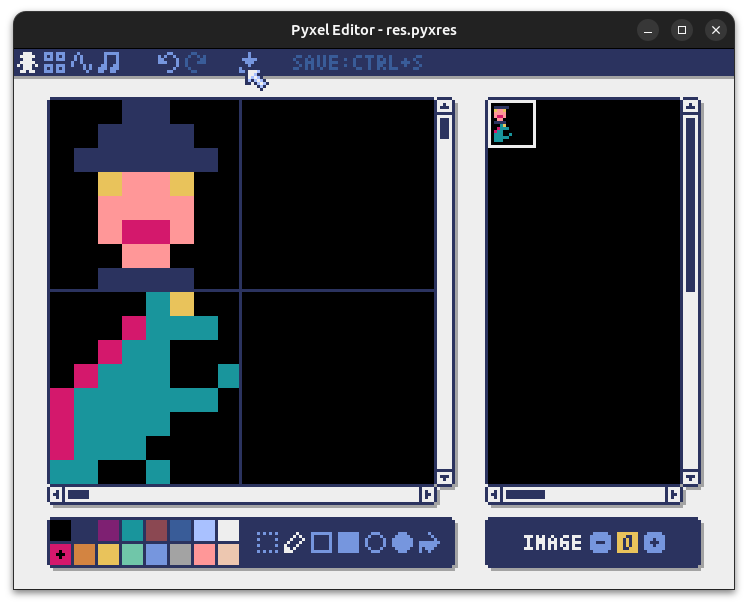
12-B° Ouvrir votre explorateur de fichier et vérifier qu'il y a bien maintenant un fichier res.pyxres dans le même répertoire que votre fichier Python.
Si ce n'est pas le cas, demandez de l'aide car vous ne pourrez pas faire la suite si les deux fichiers ne sont pas bien positionnés l'un par rapport à l'autre.
12-C° Vous allez maintenant pouvoir placer vos dessins dans votre fenêtre Pyxel. Mais pour cela, il faut d'abord pouvoir les localiser correctement.
A faire
Cliquez sur le petit crayon puis placez votre curseur à l'endroit où sont situés les petits carrés blanc, rose, jaune et violet ci-dessous.
Observez les coordonnées qui apparaissent en haut à droite.
Ci-dessous, l'exemple avec le curseur au dessus du carré jaune : on voit qu'il est en (0,8), c'est à dire colonne 0 et ligne 8.
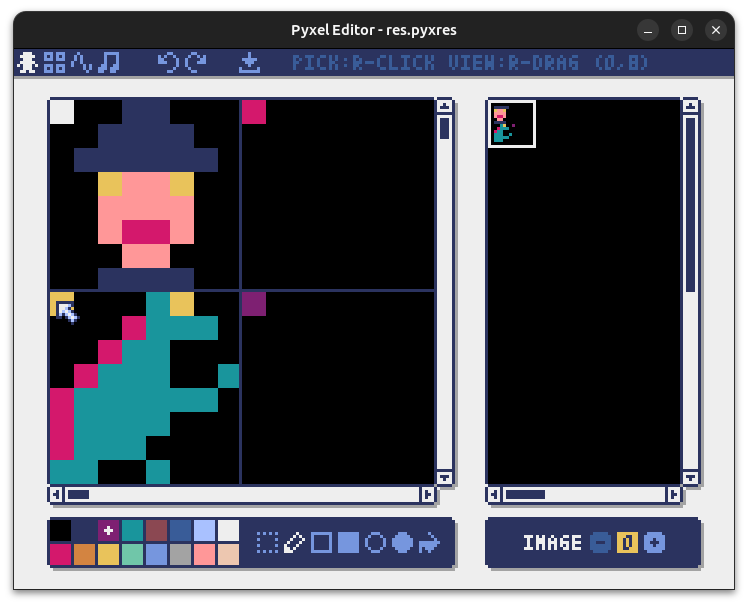
Questions
- Coordonnées (x,y) du carré blanc ci-dessus ?
- Coordonnées (x,y) du carré jaune ci-dessus ?
- Coordonnées (x,y) du carré rose ci-dessus ?
- Coordonnées (x,y) du carré violet ci-dessus ?
...CORRECTION...
- Coordonnées (x,y) du carré blanc ci-dessus ? (x=0, y=0)
- Coordonnées (x,y) du carré jaune ci-dessus ? (x=0, y= 8)
- Coordonnées (x,y) du carré rose ci-dessus ? (x=8, y=0)
- Coordonnées (x,y) du carré violet ci-dessus ? (x=8, y=8)
12-D° Sur l'écran du droite, vous avez la possibilité d'aller beaucoup plus loin sur cette carte/map. Déplacez le curseur pour visualiser qu'on peut effectivement dessiner sur d'autres parties.
Encore plus fort : cliquez sur le + et le - qui entoure le mot IMAGE en bas à droite : vous allez vous rendre compte qu'on dispose en réalité de 3 images/maps numérotées 0, 1 et 2.
Chaque map est un carré de 256 pixels sur 256 pixels.
La première coordonnée est (0,0), celle du point en bas à droite est donc (255,255) :
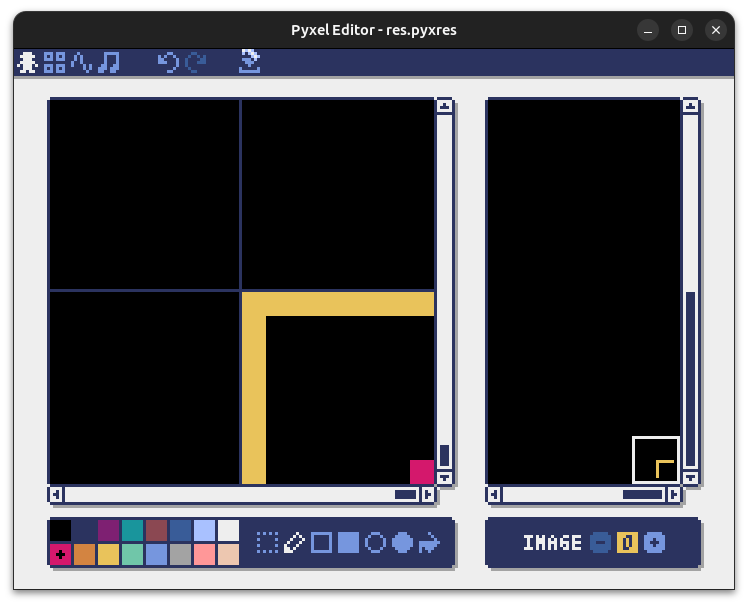
Trouvez le coin en bas à droite et vérifiez que ses coordonnées sont bien (255,255).
13-A° Afficher ces dessins se fait en deux temps. Lire les explications ci-dessous, le programme complet arrive en 13-B.
- On charge notre fichier pyxres avec la fonction load() entre init() et run() :
- Le fichier pyxres doit être au même endroit que le fichier Python.
- Il doit bien porter exactement le nom indiqué. Ici, j'ai noté laby.pyxres; si votre fichier se nomme res.pyxres cela ne fonctionnera pas.
- Ensuite, on peut utiliser cette nouvelle fonction en remplacement de rect() : la fonction blt() permet d'afficher un bloc de pixels issus de votre fichier pyxres.
1
2
3 | |
Deux conditions à respecter :
Voici son prototype :
def blt(x:int, y:int, img:int, u:int, v:int, w:int, h:int, col_key=None:int) -> None
Dessine aux coordonnées (en pixels) x, y de la fenêtre graphique une image qui se trouve sur la page numéro img.
Les coordonnées x y sont celles du coin en haut à gauche dans le fichier pyxres, la largeur et la hauteur w h permettent de connaître quel bout de l'image on désire transférer.
col_key est la couleur de transparence de cette image. Si on ne veut pas de transparence, il suffit de ne pas le transmettre lors de l'appel.
Exemple d'utilisation
On place en (50,100), un dessin tiré de l'image 0 du fichier pyxres. Le point en haut à gauche est (0,0) et on récupère un bloc de 8*8. La couleur 0 sera gérée comme couleur transparente.
7 | |
Un exemple complet :
1
2
3
4
5
6
7
8
9
10
11 | |
13-B° Voici le programme du jeu du labyrinthe mais avec affichage des dessins.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68 | |
Lancer le programme pour vérifier que les images apparaissent bien puis expliquer clairement ce que font les lignes 55-56.
...CORRECTION...
55
56 | |
En ligne 55, on place en (x,y) un bloc de 8*8 de couleur 7 (blanc).
En ligne 56, on place au même endroit (x,y) un bloc de 8*8 tiré de l'image 0 : le coin en haut à gauche est (0,8). Il s'agit donc d'un des monstres.
14-A° Pyxel affiche 30 images par seconde.
Pour créer une alternance d'images, nous allons utiliser pyxel.frame_count qui contient le nombre d'images (frames) depuis le début du jeu.
Lancer ce nouveau programme pour voir comment gérer les alternances.
Pour éviter les mauvaises synchronisations, nous avons fait ceci :
- On crée une variable globale horloge qui contiendra
- horloge[0] le nombre de frames depuis le lancement ;
- horloge[1] le nombre de secondes écoulées depuis le début du jeu
- horloge[2] le nombre de frames depuis la dernière seconde : un entier entre 0 et 29 donc.
- Dans controler(), nous allons mettre à jour les trois cases de horloge.
- Dans afficher() nous allons lire horloge pour créer l'alternance entre deux affichages.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29 | |
Quelques explications supplémentaires à comprendre pour la question suivante.
L'opérateur // renvoie le quotient d'une division euclidienne et l'opérateur % son reste.
Regardons ce que cela donne si 300 frames se sont écoulées :
300 │ 30
├────
reste 0 │ 10
>>> 300 // 30
10 # 10 secondes depuis le début du jeu
>>> 300 % 30
0 # 0 frame depuis le début de la seconde
C'est logique : 300 = 30*10 + 0.
Regardons ce que cela donne si 320 frames se sont écoulées :
320 │ 30
├────
reste 20 │ 10
>>> 320 // 30
10 # 10 secondes depuis le début du jeu
>>> 320 % 30
20 # 20 frames depuis le début de la dernière seconde
C'est logique : 320 = 30*10 + 2.
Comme il y a 30 images par secondes, s'il y a plus de 15 frames depuis le début de la dernière seconde, c'est qu'on est dans la deuxième partie de la seconde qui s'écoule.
Le reste de la division euclidienne va donc nous permettre de gérer assez finement les intervalles de temps.
14-B° Voici le programme du labyrinthe qui utilise cela pour créer une alternance sur le personnage et les monstres.
L'affichage du temps se fait à travers une nouvelle fonction que j'ai nommé afficher_temps().
Voici le programme modifié :
- Lancer pour voir le résultat ;
- Lire les zones modifiées (en jaune) pour comprendre comment il fonctionne ;
- Rajouter les blocs de pixels qu'il vous manque dans votre fichier pyxres pour créer une alternance.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85 | |
15° Mais que contient le fichier d'extension .pyxres ? Pourquoi parler d'animation avec Pyxel dans un cours sur les matrices ?
Pour le savoir, aller dans l'exploration de fichiers. En double-cliquant sur le fichier, vous allez voir qu'il ne s'agit que d'un fichier texte compressé.
Ouvrez le fichier : vous devriez tomber sur un code-source et voir que les données des images sont mémorisées... dans une matrice, un tableau de tableaux.
7 - Pour aller plus loin : un vrai jeu
16° Pour finir, nous allons permettre au personnage puis aux monstres de se déplacer sur le plateau de jeu.
Pour cela, nous allons placer les données du joueur et des monstres dans des tableaux de trois cases : [nC, NL, vie], vie étant un entier caractérisant les points de vie de ces individus.
Questions
- Compléter le schéma d'appels des fonctions en lisant le code fourni et en rajoutant les fonctions qui ne sont pas présentes ci-dessous :
- Observer la fonction mouvement_joueur() pour comprendre ce qu'elle réalise.
- Compléter la fonction
- Compléter alors la fonction deplacer_joueur(), largement incompléte. On veut que le joueur puisse se déplacer si la case de destination est vide et perde une vie s'il tombe sur un monstre ou sur un mur.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140 | |
...CORRECTION...
La structure du programme est visible juste sous cette correction.
Voici le code de la fonction modifiée :
1
2
3
4
5
6
7
8
9
10
11
12
13
14 | |
La structure générale du programme est donc celle-ci pour le moment :
17° Il vous reste à gérer les monstre.
Compléter la dernière fonction
- Déterminer aléatoirement si le monstre veut aller à gauche, à droite, en haut ou en bas ;
- Vérifier la nature de la case de destination ;
- Si la case est vide, il y va ;
- Si la case contient le joueur, il n'y va pas mais le joueur perd un point de vie.
...CORRECTION...
Ceci n'est qu'une proposition de correction. Il y a plein de façons de faire cela.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27 | |
18° Agrandir la matrice et placer deux nouveaux codes de cases qui pourrait être le code d'un trésor à ramasser et le code d'une clé pour ouvrir ce trésor. Cela devrait vous rappeller des choses.
19° Rajouter les graphismes pour le coffre et la clé.
20° Finaliser le jeu : lorsqu'on ouvre le coffre, un beau message félicite le joueur.
Si le joueur a moins de 1 pv, il faudra vous arranger pour relancer le jeu.
8 - FAQ
Comment avoir une matrice XY plutôt que YX
Cette partie vous montre comment pouvoir écrire mat[x][y] plutôt que mat[y][x].
1e solution : tableau de colonnes pour écrire [x][y]
La première solution serait de créer un tableau de colonnes plutôt qu'un tableau de lignes. Pas top, mais fonctionnelle.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 | # Anciennes données en lignes : claires pour un humain mais [y][x]
ligne0 = [1, 0, 0, 1, 1, 0]
ligne1 = [1, 0, 3, 1, 1, 0]
ligne2 = [1, 0, 0, 0, 3, 0]
ligne3 = [8, 0, 0, 0, 1, 1]
ligne4 = [1, 0, 1, 0, 1, 0]
ligne5 = [1, 0, 1, 0, 0, 0]
# Nouvelles données en colonnes : permet d'écrire [x][y]
colonne0 = [1, 1, 1, 8, 1, 1]
colonne1 = [0, 0, 0, 0, 0, 0]
colonne2 = [0, 3, 0, 0, 1, 1]
colonne3 = [1, 1, 0, 0, 0, 0]
colonne4 = [1, 1, 3, 1, 1, 0]
colonne5 = [0, 0, 0, 1, 0, 0]
mat = [colonne0, colonne1, colonne2, colonne3, colonne4, colonne5]
print(mat[4][2])
|
2e solution : transformer le tableau de lignes en tableau de colonnes
Deux étapes : on crée un tableau pour qu'il soit facile à taper et à lire pour un humain et ensuite on le transforme en tableau de colonnes automatiquement.
Le probmème vient juste de la double place mémoire lors de la phase de création.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 | # Etape 1 : on crée les données en les présentant en lignes
ligne0 = [1, 0, 0, 1, 1, 0]
ligne1 = [1, 0, 3, 1, 1, 0]
ligne2 = [1, 0, 0, 0, 3, 0]
ligne3 = [8, 0, 0, 0, 1, 1]
ligne4 = [1, 0, 1, 0, 1, 0]
ligne5 = [1, 0, 1, 0, 0, 0]
mat = [ligne0, ligne1, ligne2, ligne3, ligne4, ligne5]
# Etape 2 : on crée le tableau de colonnes à partir de la matrice de base
nbrL = len(mat)
nbrC = len(mat[0])
mat2 = [ [ mat[y][x] for y in range(nbrL) ] for x in range(nbrC) ]
# Etape 3 : on vérifie que les deux matrices pointent bien la même case
print(mat[2][4])
print(mat2[4][2])
|
La ligne centrale est la ligne 17 : on crée un tableau de tableaux en utilisant deux créations par compréhension imbriquées l'une dans l'autre.
.Remarquez bien que cette ligne 17 revient à écrire mat2[x][y] = mat[y][x].
Activité publiée le 10 06 2020
Dernière modification : 16 03 2025
Auteur : ows. h.