29 - Vocabulaire des graphes
Page qui reprend l'essentiel des notions à comprendre.
Modification prévue pour l'année prochaine :
- L'activité précédente contiendra activité et cours sur le vocabulaire basique indiqué dans le programme.
- Cette activité contiendra activité et cours sur le vocabulaire supplémentaire pratique pour l'épreuve du grand oral.
Documents de cours : open document ou pdf
1 - Vocabulaire commun des cours de NSI
Les graphes sont des objets mathématiques très utilisés, notamment en informatique.
Ils se prêtent très bien à la modélisation d'un nombre important de problèmes, notamment ceux impliquant de grands nombres de relations entre différentes entités :
- Relations sociales : relations entre des individus
- Réseaux routiers : relations entre des croisements (carrefours, ronds-points, échangeurs d'autoroute)
- Réseaux Internet : relations entre des routeurs
- Plan du Web : relations entre les sites Web (liens)
- Automates : relations entre les états de l'automate
- Bases de données : relation entre les tables.
- Gestion de projets : relation entre les différentes parties du projet
- ...
Un ensemble ne peut contenir que des éléments distincts. On les note en utilisant les accolades.
{4, 40, 400, 4000} est un ensemble.
{4, 4, 400, 4000} n'est pas un ensemble.
Si on veut décrire une succession d'éléments dont certains sont identiques, on doit passer par une autre notation, comme le p-uplet par exemple :
(4, 4, 400, 4000).
Rappel : Vocabulaire à connaître
Dans le rappel ci-dessous, les mots de vocabulaire à connaître pour l'épreuve sont surlignés. Les autres mots ne sont fournis qu'à titre de culture générale et de façon à comprendre certaines lectures que vous allez peut-être trouver sur le Web (lors de la préparation du Grand Oral par exemple).
Les graphes orientés et non orientés sont parfois munis d'un vocabulaire spécifique pour les distinguer : nous n'utiliserons pas ces termes ici. Voir la FAQ si vous rencontrez un terme "étrange" dans vos lectures.
Les termes à connaître et officiellement présents dans le BO sont :
- Structure relationnelle
- Graphe orienté et graphe non orienté
- Sommet
- Arc et Arête
- Chemin
- Cycle
2 - Graphe non orienté et graphe orienté
1 - Généralités sur les graphes
Un graphe G est constitué :
- d’un ensemble fini S de points appelés sommets.
- les sommets des graphes sont l'équivalent des noeuds des arbres : ils ont une étiquette et des données rattachées.
- Sur l'exemple, les étiquettes des sommets sont a, b, c, d, e et f.
- De façon plus formelle, on peut définir l'ensemble S de cete façon : S = {a, b, c, d, e, f} S étant un ensemble de sommets, les sommets sont nécessairement tous distincts.
- d’un ensemble fini A de relations nommés soit arêtes, soit arcs, qui relient deux sommets qu'on nomme les extrémités.
- Les arêtes sont les relations d'un graphe non orienté.
- Les arcs sont les relations d'un graphe orienté.
- Un graphe est connexe lorsqu'on peut atteindre n'importe quel sommet depuis n'importe quel sommet.
- Un graphe est donc bien une structure relationnelle car il renseigne sur les relations entre ces sommets. On utilise parfois une notation mathématique montrant qu'un graphe est un couple composé de l'ensemble S des sommets et de l'ensemble A des relations entre les sommets :
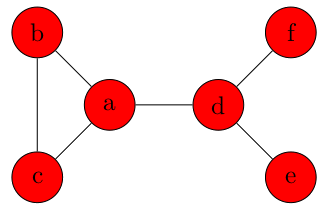
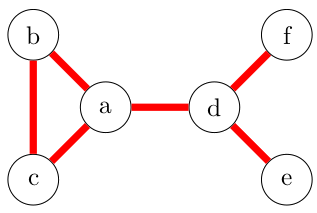
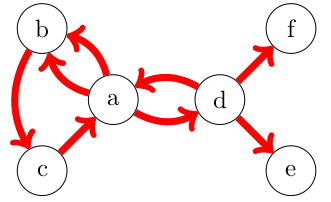
Le graphe G non orienté ci-dessus est connexe.
Le graphe G orienté ci-dessus n'est pas connexe car partant de f ou de e on ne peut pas atteindre n'importe quel autre sommet.
G = (S, A)
2 - Graphes non orientés
Si le graphe est non-orienté, la relation entre deux sommets se nomme une arête

- L'arête a-b permet de se déplacer aussi bien de a vers b que de b vers a
- Dans un graphe simple non orienté (définition donné plus loin), on représente une arête a-b comme un ensemble {a,b} pour indiquer {a,b} est bien équivalent à {b,a}.
- L'ensemble S des arêtes du graphe de l'exemple est un ensemble d'ensembles :
- des sommets reliés par une arête sont dits adjacents ou voisins
- des arêtes menant au même sommet sont dites adjacentes
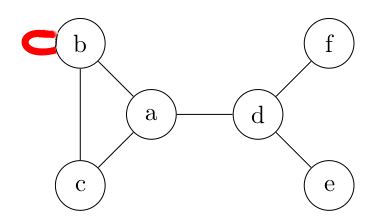
- Boucle : IMPOSSIBLE de façon rigoureuse dans un graphe simple non-orienté.
- Il s'agit d'une sorte d'arête partant d'un sommet et revenant directement à ce sommet.
- Cela n'est pas possible rigoureusement dans un graphe non orienté car il faudrait écrire {b,b} pour décrire la boucle. Or, un même élément ne peut apparaître deux fois dans un ensemble.
- Un graphe non orienté contenant une boucle est donc une variante d'un graphe non orienté qui ne respecte pas exactement les notations vues ci-dessus.
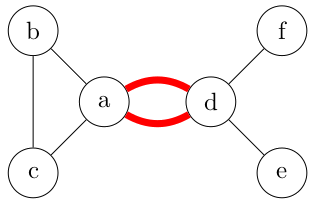
- Arêtes multiples : IMPOSSIBLE dans un graphe simple non orienté.
- Il s'agit de plusieurs arêtes ayant les mêmes extrémités et permettant donc de passer d'un sommet à l'autre par plusieurs chemins directs.
- Sur l'exemple, a et d sont en relation à travers deux arêtes distinctes. Cela pourrait schématiser deux salles reliées par deux portes différentes.
- Cela n'est pas possible dans un graphe simple non orienté puisqu'on ne décrit une arête que par ses extrémités ({a,d} par exemple). Il faudrait ici écrire E = { ... {a,d},{a,d} ... }. Or, on ne peut pas placer deux fois une même élément dans un ensemble.
- Définition : graphe simple non orienté
- Il s'agit d'un graphe non orienté qui ne possède ni boucle, ni arêtes multiples.
- En NSI,graphe non orienté signifie de façon implicite graphe simple non orienté.
S = { {a,b}, (a,c), {b,c} {a,d}, {d,f}, {d,e} }
Sur le graphe de l'exemple, les sommets a et b sont adjacents. Par contre, a et e ne sont pas adjacents.
Sur le graphe de l'exemple {a,b} et {b,c} sont deux arêtes adjacentes car les deux mènent à un sommet commun c.
3 - Graphe orienté
Si le graphe est orienté, la relation entre deux sommets se nomme un arc (moyen mnémotechnique : il y a une flèche, arc et flèche).

- il existe un "sens de circulation" : il est possible qu'on puisse aller de a vers b sans pouvoir aller de b vers a (typique de la rue à sens unique)
- on représente un arc avec la notation (a,d) pour indiquer a vers d. S'agissant d'un couple (un 2-uplet), l'arc (a,d) est différent de l'arc (d,a).
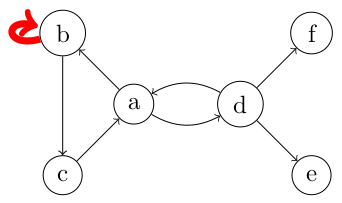
- Boucle : possible avec un graphe orienté
- Il s'agit d'un arc partant d'un sommet et revenant directement au même sommet.
- Les boucles sont possibles dans un graphe simple orienté car on peut écrire le couple (b, b) par exemple.
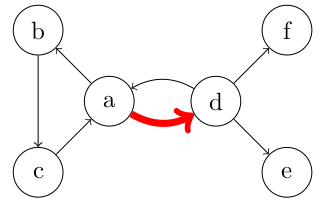
- Arcs multiples : IMPOSSIBLE dans un graphe simple orienté
- Il s'agit de plusieurs arcs ayant la même extrémité initiale et la même extrémité finale permettant donc de passer d'un sommet à l'autre par plusieurs chemins directs.
- Sur l'exemple, on voit qu'il existe deux "arêtes multiples" permettant d'aller de a vers d.
- Cela n'est pas possible dans un graphe simple puisqu'on peut voir qu'il faudrait utiliser une notation de ce type pour décrire l'ensemble des arcs (or un ensemble ne peut pas contenir deux fois le même élément)
- Les arcs multiples ne seront pas étudiés cette année.
- Définition : Graphe simple orienté
- Il s'agit d'un graphe orienté pouvant contenir des boucles mais pas d'arcs multiples.
- Notez bien ici que les deux arcs entre a et d ne sont pas les mêmes : nous avons (a,d) et (d,a). Il ne s'agit donc pas d'arcs multiples.
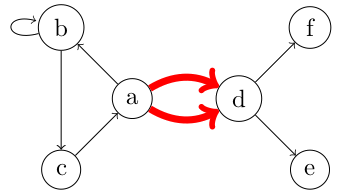
A = {... (a,d),(a,d) ...}
3 - Chemin
L'étude du cheminement dans un graphe est fondamentale et définir clairement le vocabulaire lié permet de catégoriser facilement le problème à résoudre.
4 - Cheminement dans le graphe orienté
- Chemin : un parcours du graphe suivant une suite précise de sommets adjacents et d'arcs adjacents.
- Exemple : d-(d-a)-a-(a,b)-b-(b,c)-c.
Dans un graphe simple, on peut donc décrire ce chemin comme - une suite d'arcs : (d-a)-(a,b)-(b,c)
- une suite de sommets : d-a-b-c
- Boucle : circuit constitué d'un seul arc qui part d'un sommet et y revient.
- Cycle
- Chemin comportant plus d'un arc et dont le sommet d'arrivée est le sommet de départ (on part de A et on revient à A).
- Si le "cycle" ne comporte qu'un arc, on parlera plutôt de boucle.
- Exemple : (d-a)-(a,b)-(b,c)-(c,a)-(a,d) par exemple.
- Acyclique.
- Un graphe orienté qui ne possède pas de cycle simple est dit acyclique.
- Chemin simple
- Définition : un chemin simple est un cheminement où on emprunte un arc donné qu'une fois au maximum.
- Le chemin et le cycle précédent sont bien des chemins simples.
- Un chemin simple passant par tous les arcs d'un graphe donné est un chemin eulérien. On notera que dans un chemin eulérien on peut emprunter plusieurs fois un même sommet.
- Le chemin dabcad n'est pas un cycle eulérien puisqu'on n'emprunte pas tous les arcs disponibles.
- Chemin élémentaire
- Définition : un cheminement élémentaire est un cheminement qui ne passe qu'une seule fois par un sommet donné.
- Le chemin dabcad précédent n'est pas élémentaire puisqu'on passe plusieurs fois par le sommet a ou le sommet d.
- Un chemin élémentaire passant par tous les sommets d'un graphe donné est un chemin hamiltonien.
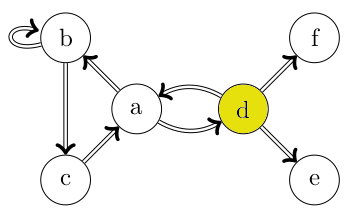
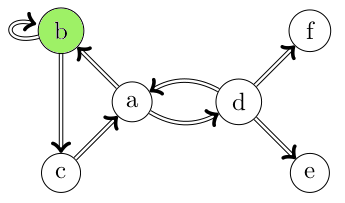
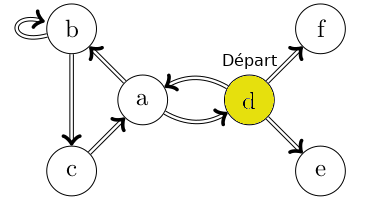
Cliquez sur l'image pour lancer l'animation
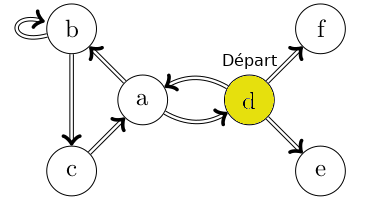
Lors d'un chemin simple, on ferme donc progressivement l'accès futur des arcs utilisés.
Lors d'un chemin élémentaire, on ferme donc progressivement l'accès futur des sommets déjà visités.
5 - Cheminement dans le graphe non orienté
On retrouve les mêmes définitions en remplaçant simplement les arcs par les arêtes. Mais vous allez voir que les chemins obtenus ne sont néanmoins pas les mêmes.
- Chemin : suite d'arêtes adjacentes successives.
- Activation des deux arcs équivalents à une arête
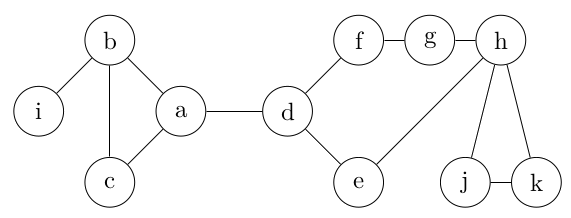
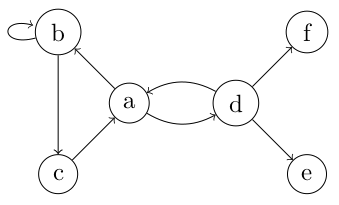
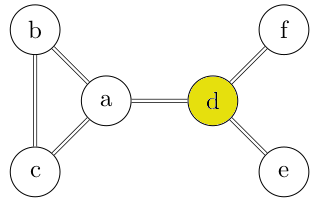
- Dans le cadre d'un chemin simple sur un graphe non orienté, l'utilisation d'une arête bloque ensuite l'accès aux deux arcs équivalents même si on décide de représenter le graphe non orienté par son graphe orienté "équivalent" ! Exemple sur le graphe ci-dessous où on pourrait se dire que représenter le graphe du bas comme un graphe orienté revient juste à remplacer chaque arête par deux arcs.
- Et bien non :
- Cycle
- Chemin (de plus d'une arête) dont les deux extrémités sont identiques (on part de A et on revient à A).
- Acyclique
- Un graphe non orienté qui ne possède pas de cycle est dit acyclique.
- Chemin simple :
- Définition : chemin où on emprunte une arête donnée une fois au maximum.
- Un chemin simple passant par tous les arêtes d'un graphe donné est un chemin eulérien. On notera que dans un chemin eulérien on peut emprunter plusieurs fois un même sommet.
- Chemin élémentaire
- Définition : un cheminement élémentaire est un cheminement qui ne passe qu'une seule fois par un sommet donné.
- Le chemin dabca précédent n'est pas élémentaire puisqu'on passe plusieurs fois par le sommet a.
- Un chemin élémentaire passant par tous les sommets d'un graphe donné est un chemin hamiltonien.
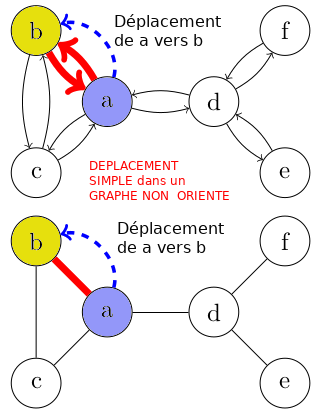
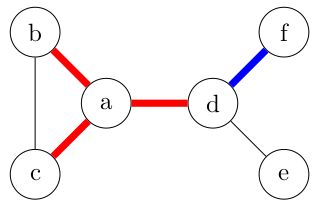
Si le graphe est non orienté, on bloque l'arête {a,b} ou les deux arcs équivalents (a,b) et (b,a).
Si le graphe était vraiment orienté, se déplacer de a vers b ne bloque que (a,b). On pourrait encore emprunter (b,a).
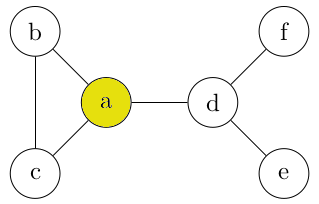
Lors d'un chemin simple, on ferme donc progressivement l'accès futur des arêtes utilisées. Le chemin dabca est un chemin simple.
Lors d'un chemin élémentaire, on ferme donc progressivement l'accès futur des sommets déjà visités.
4 - Traduction
En anglais - culture générale bien entendu
- Directed Graph ou Digraph pour Graphe Orienté et Arc pour Arc
- Undirected Graph pour Graphe Non Orienté et Edge pour Arête
- Vertex pour Sommet
- Edge pour arête
- Walk pour Chemin
- Trail pour Chemin Simple
- Loop pour Boucle
- Cycle pour Cycle
Ceux qui utilisent Blender devraient reconnaître ces termes.
5 - FAQ : vocabulaire plus détaillé
Attention, ces mots ne devraient normalement pas se trouver dans les sujets de NSI. Je ne les donne que pour que vous puissiez comprendre les documents trouvés sur le Web lors de vos recherches, notamment pour l'épreuve du grand oral.
Le vocabulaire associé aux deux types de graphes
On utilise parfois des termes différents. Ce vocabulaire spécifique n'est pas à connaître pour la NSI : je n'en parle ici que pour que vous puissiez comprendre les pages ou livres que vous allez trouver sur le sujet.
Attention : cette classification n'est pas standardisée, le mot est faible. Il est donc possible qu'un terme dédié ici au cas non orienté soit utilisé dans un contexte orienté, ou l'inverse...
| Terme NSI | Graphe orienté | Graphe non orienté |
|---|---|---|
| Sommet | Sommet ou noeud ou point | Sommet ou noeud ou point |
| Arc ou Arête | Arc, flèche, ligne, lien | Arête, flèche, ligne, lien |
| Chemin | Chemin | Chaîne |
| Chemin simple | Chemin simple | Chaîne simple |
| Chemin élémentaire | Chemin élementaire | Chaîne élémentaire |
| Boucle | Boucle | Boucle |
Ordre d'un graphe ?
Ici, on obtient 6.
Il s'agit de l'équivalent de la taille d'un arbre.
Degré d'un sommet ?
Pour un graphe non orienté
- Exemple : le degré de a est 3, le degré de f est 1.
Pour un graphe orienté
Activité publiée le 08 04 2021
Dernière modification : 16 03 2022
Auteur : ows. h.