30 - graphe et matrice

⏪

⏬

⏩

1 - rappels

2 - Mx adjacence

3 - Graphes pondérés

4 - Graphes orientés

5 - Python

6 - FAQ

Nous avons vu cette année :

Des structures de données linéaires : les piles, les files et les listes, dont

Les listes contiguës : les tableaux
Les listes chaînées

Des structures arborescentes : les arbres
Des structures relationnelles : les graphes

Pour chacun de ces types abstraits, nous avons présenté plusieurs représentations abstraites avant de réaliser des implémentations en structures de données réelles.

Nous allons faire de même avec les graphes aujourd'hui.

MODE COURS (cacher les questions)

1 - Rappels sur les graphes

⇩ ⇧ ⤊

Allez lire l'activité précédente si vous n'en venez pas : elle précise tout un tas de mots de vocabulaire qui vont être rencontrés ici.

Résumé du vocabulaire

2 - Matrice d'adjacence

⇩ ⇧ ⤊

Dans la théorie des graphes, la matrice d'adjacence d'un graphe est une matrice qui décrit le graphe en permettant de connaître les arêtes (ou les arcs) reliant les différents sommets.

Matrice 2D

Matrice vue comme un tableau 2D

Une matrice (à deux dimensions) est un tableau de données à deux entrées avec

L lignes et
C colonnes

Si L = C, on dit que la matrice est carrée.

Cette matrice est de taille (L, C) (on la donne toujours dans l'ordre lignes, colonnes).

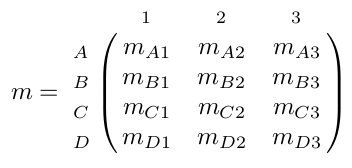
Sur notre exemple :

Les lignes sont étiquetées A, B, C et D.
Les colonnes sont étiquetées 1, 2 et 3.
La taille de cette matrice est donc (4,3).

Contenu de la matrice

On parvient à retrouver facilement le contenu de la matrice en fournissant la ligne et la colonne voulue.

Exemple avec la position du contenu associé à (B,3) :

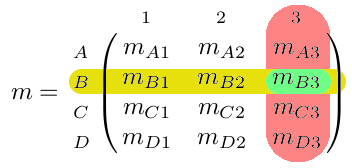
Donnons un contenu de type entier à notre matrice :

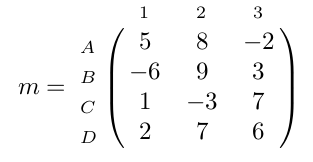
m_A1 = 5
m_A2 = 8
m_B3 = 3
m_C3 = 7
m_D1 = 2

Lignes-Colonnes en indice numérique pur

On donne la plupart du temps uniquement des numéros aux lignes et aux colonnes plutôt que des étiquettes comme A, B, C...

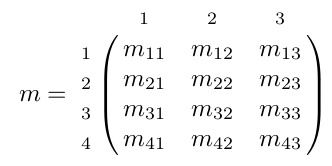
On notera qu'on indique bien m_LC pour ligne-colonne.

Ainsi m₃₂ veut dire 3e ligne et 2e colonne.

01° Donner les valeurs associées à m₅₂ et m₄₃ en vous basant sur la matrice suivante :

Correction ?

...CORRECTION...


m₅₂ = 7
m₄₃ = 6

02° Pourquoi peut-on dire qu'il s'agit d'une matrice carrée ?

Correction ?

...CORRECTION...

Carrée car même nombre de lignes et de colonnes.

Et quel est le lien avec les graphes ?

L'un des moyens de représenter un graphe par une matrice est de créer une matrice dite d'adjacence.

Matrice d'adjacence d'un graphe non orienté

Il suffit d'identifier chaque sommet par un numéro et on indique dans la matrice

l'existence d'une arête entre le sommet i et le sommet j en plaçant m_ij = 1
l'absence d'une arête entre le sommet i et le sommet j en plaçant m_ij = 0

Matrice exemple pour la matrice d'adjacence

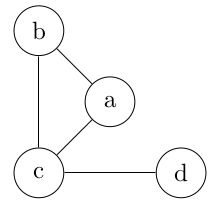
Prenons simplement 1 pour a, 2 pour b, 3 pour c et 4 pour d.

m_aa = 0 ou m₁₁ = 0 : pas de boucle sur a

m_ab = 1 ou m₁₂ = 1 : il y a une arête entre a et b

m_ac = 1 ou m₁₃ = 1 : il y a une arête entre a et c.

m_ad = 0 ou m₁₄ = 0 : pas d'arête avec d

La ligne caractérisant les arêtes de a est donc 0 1 1 0.

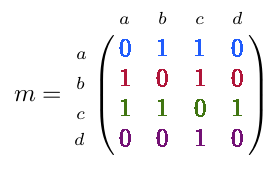
03° En vous aidant uniquement de la deuxième ligne (en rouge), donner les cases de la matrice non nulles sur cette ligne (à l'aide d'une notation de type m_ij). En déduire quelles sont les arêtes issues du sommet b.

Correction ?

...CORRECTION...

m₂₁ = 1 et m₂₃ = 1

On en déduit la présence des arêtes {a, b} et {b, c}.

04° En vous aidant uniquement de la troisième ligne (en vert), donner simplement le nombre d'arêtes issues de c.

Ce nombre se nomme le degré du sommet.

Correction ?

...CORRECTION...

La ligne contient 3 "1". On en déduit que le sommet c possède 3 arêtes.

Son degré est d = 3.

05° En vous aidant uniquement de la quatrième ligne (en violet), donner simplement le nombre d'arêtes issues de d.

Ce nombre se nomme le degré du sommet.

Correction ?

...CORRECTION...

La ligne contient un seul "1". On en déduit que le sommet d possède 1 arête.

Son degré est d = 1.

Matrice symétrique pour un graphe non orienté

On remarquera que la matrice d'adjacence d'un graphe non orienté est symétrique par rapport à la diagonale.

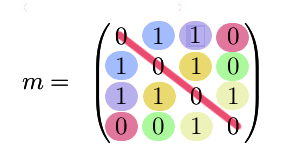
La matrice d'adjacence d'un graphe non orienté est donc nécessairement symétrique puisqu'elle contient des informations sur les arêtes qui sont des relations symétriques.

Ainsi si m₁₂ = m₂₁ par exemple.

Si on généralise, on peut écrire m_ij = m_ji

Implémentation d'un graphe : on voit donc qu'on peut supprimer la moitié supérieure ou la moitié inférieure de façon à limiter la place mémoire lors de l'implémentation. Inutile de travailler sur un vrai tableau à double entrée.

06° En utilisant la propriété précédente de symétrie pour gagner du temps, déterminer la matrice d'adjacence du graphe non orienté ci-dessous.

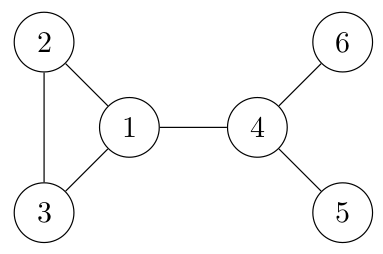
Pour cela, demandez vous

Quelles sont les arêtes du sommet 1 ?
Quelles sont les arêtes du sommet 2 menant à 2 ou plus ?
Quelles sont les arêtes du sommet 3 menant à 3 ou plus ?
Quelles sont les arêtes du sommet 4 menant à 4 ou plus ?
Quelles sont les arêtes du sommet 5 menant à 5 ou plus ?
Le sommet 6 possède-t-il une boucle vers lui-même ?

Il faudra donc compléter une matrice qui ressemble à cela (vous ne cherchez à remplacer que les points d'interrogation):

Finir en complétant la matrice par symétrie.

Correction ?

...CORRECTION...

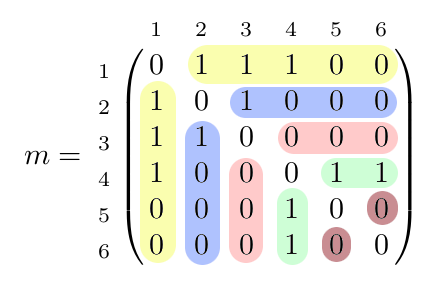
07° On rajoute simplement deux boucles par rapport au graphe précédent.

Questions

Que va devenir la matrice ?
Est-ce vraiment un graphe simple non orienté ?

Correction ?

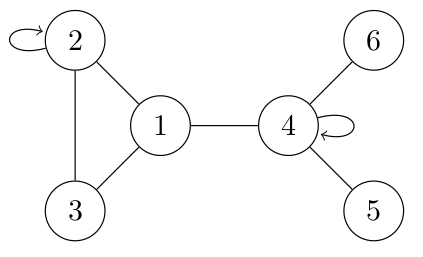
...CORRECTION...

On rajoute simplement m₂₂ = 1 et m₄₄ = 1.

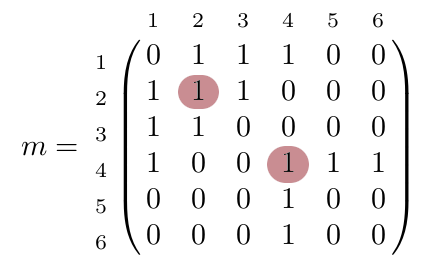
Il s'agit d'un graphe non orienté mais pas d'un graphe SIMPLE non orienté. En effet, les arêtes sont caractérisées comme un ensemble contenant les deux extrémités des sommets reliés par l'arête. Or la boucle sur 2 devrait être alors caractérisée par {2,2}, ce qui n'est pas possible de façon rigoureuse : un ensemble ne peut pas contenir deux fois le même élément. Nous travaillons donc ici sur un variante de graphe non orienté et pas sur un vrai graphe simple non orienté.

Voyons l'influence (ou pas) des noms des sommets.

08° Voici deux graphes. Leurs matrices d'adjacente m sont-elles différentes ?

Correction ?

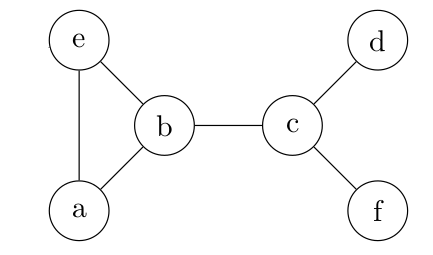
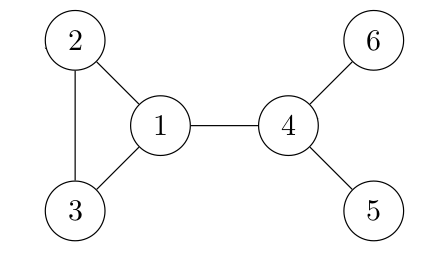
...CORRECTION...

Non, la matrice reste la même, pourvu qu'on garde une numérotation cohérente par rapport au cas précédent.

Voyons l'influence (ou pas) des positions graphiques des sommets.

09° On a simplement changé les positions graphiques de quelques sommets. Cela va-t-il changer quelque chose pour la matrice m ?

Correction ?

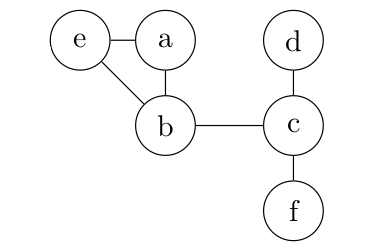
...CORRECTION...

Non, la position des sommets dans la représentation graphique n'a aucune influence sur la matrice représentant le problème.

10° Et cette fois ?

Correction ?

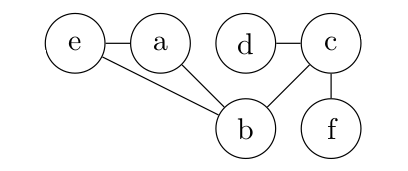
...CORRECTION...

Toujours la même matrice et le même graphe. La position des sommets dans la représentation graphique n'a aucune influence sur la matrice représentant le problème.

Maintenant que vous avez vu qu'on peut transposer un problème sous forme d'un graphe sans se préoccuper de la "forme réelle" du problème pour représenter le graphe, maintenant que vous avez vu que la forme du graphe n'a pas d'influence sur sa matrice d'adjacence tant que les arêtes restent les mêmes, vous allez pouvoir représenter les matrices de quelques problèmes réels.

11° Réaliser le graphe de votre maison. Vous vous limiterez à 6 pièces au maximum. Chaque sommet représentera l'une des pièces. Les couloirs, escaliers et autres zones seront représentés par une arête si ils ne mettent que deux pièces en relation, comme un sommet dans les autres cas.

Remarque : il est possible que votre maison ne soit pas représentable sous forme d'un graphe simple si plusieurs portes ménent d'une pièce A à la même pièce B...

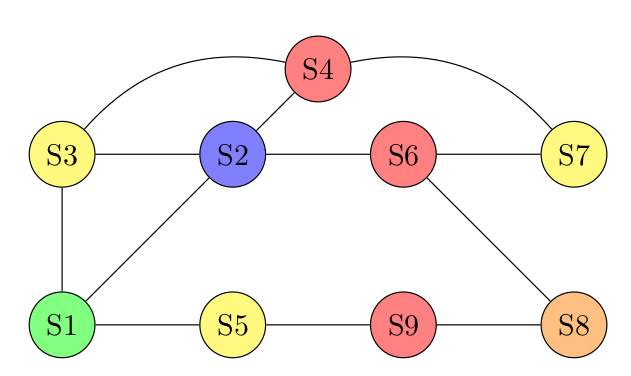
Nous allons travailler sur Pacman en simplifiant son plateau dans le cas d'un simple problème de sortie de labyrinthe. Les cases du plateau sont regroupées en zone. Les sommets du graphe sont donc juste des zones et les arêtes permettent de passer d'une zone à une autre. Voici le résultat de la simplification pour le quart supérieur gauche :

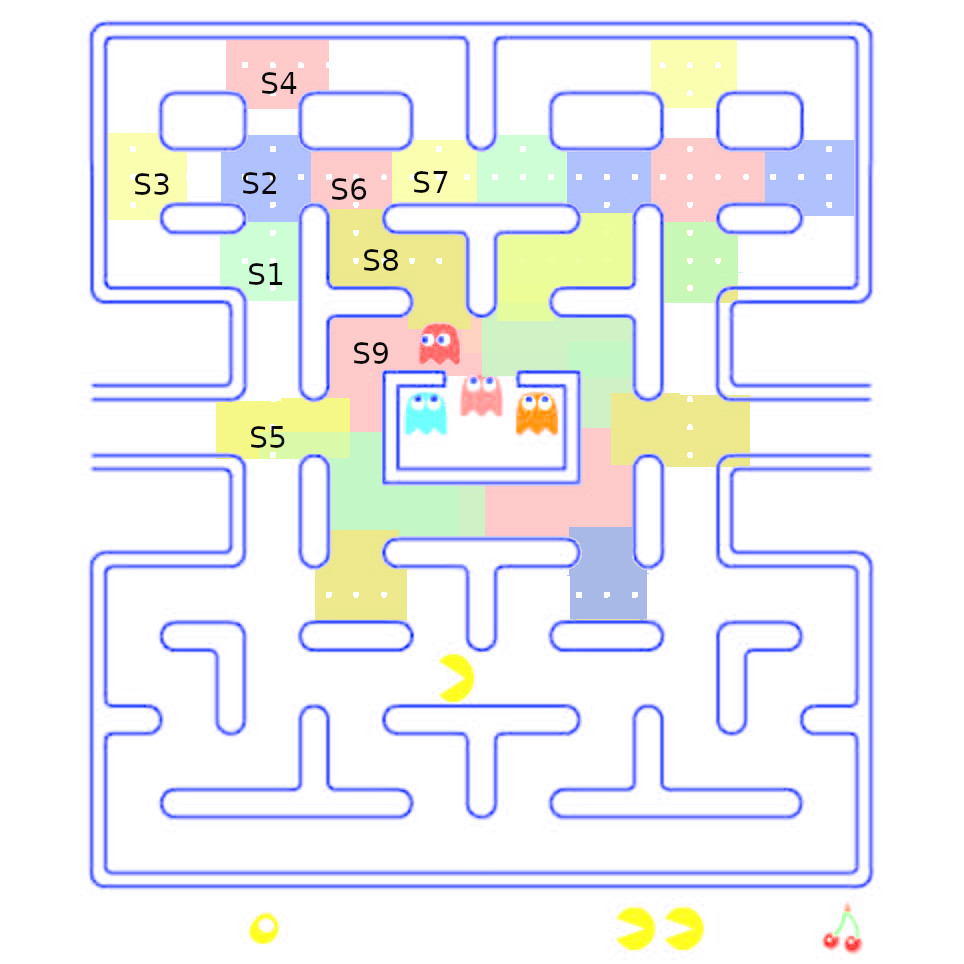
12° Vérifier la concordance (ou pas) entre ce graphe et le plateau de jeu de Pacman en réalisant la matrice d'adjacence des deux représentations :

Commencez par chercher les arêtes du sommet 1
Cherchez ensuite les arêtes du sommet 2 avec les sommets 3 et plus.
Cherchez ensuite les arêtes du sommet 3 avec les sommets 4 et plus.
...

Correction ?

...CORRECTION...

13° Vérifier la concordance (ou pas) entre cette matrice symétrique et le graphe ou le plateau de jeu de Pacman en comptant simplement le nombre d'arêtes (le degré) des sommets un par un et en comparant au nombre de "1" présent sur la ligne puis la colonne de ce sommet.

Par exemple, S1 possède 3 arêtes et sa ligne et sa colonne contiennent bien 3 "1".

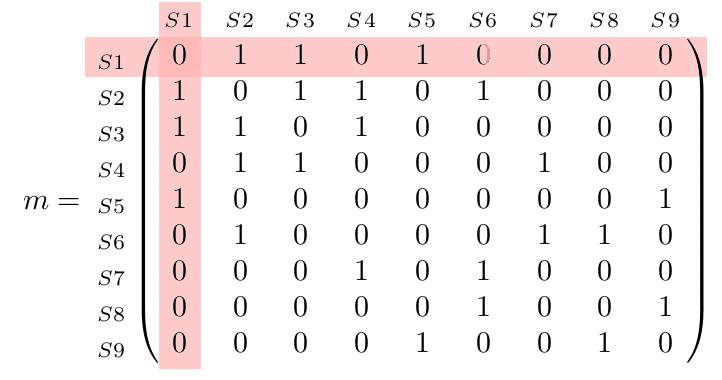
14° La matrice précédente contient 9x9 soit 81 cases.

Si une matrice contient une grande proportion de 0, on dit qu'elle est creuse. En terme de matrice d'adjacence, cela veut dire que les sommets sont peu couplés entre eux.

Si une matrice contient peu de 0, on dit qu'elle est dense. En terme de matrice d'adjacence, cela veut dire que les sommets sont fortemenet couplés entre eux.

Répondre aux questions suivantes :

La matrice contient-elle plus de "0" ou de "1" ?
Cette matrice est-elle plutôt dense ou creuse ?
Le coût en mémoire d'une matrice d'adjacence est-il logarithmique, linéaire ou quadratique ?
Utilisez une matrice d'adjacence est-il pertinent en terme de place mémoire lorsqu'on travaille sur un système possèdant beaucoup de sommets mais avec un couplage peu important ?

Correction ?

...CORRECTION...

La matrice contient beaucoup plus de 0 que de 1.

Les sommets du graphe correspondant sont en effet plutôt peu couplés entre eux.

On obtient donc plutôt une matrice creuse.

En terme de mémoire, un graphe de n sommets nécessite n² cases. Le coût mémoire est donc quadratique.

On se doute donc bien qu'il ne sera pas nécessairement judicieux d'utiliser cette façon de faire si les sommets sont peu couplés entre eux.

3 - Cas des graphes pondérés

⇩ ⇧ ⤊

Pour l'instant, on ne mémorise finalement que la présence d'une liaison, ou pas.

On peut également rajouter la notion de poids de l'arête ou de coût d'utilisation de la liaison.

Concrêtement, cela peut correspondre :

A la distance entre deux villes pour un système d'itinéraire
Au temps pour joindre deux villes pour ce même système
Au coût OSPF entre deux routeurs pour un système autonome
...

Nous allons donc retrouver notre problème du voyageur de commerce par exemple :

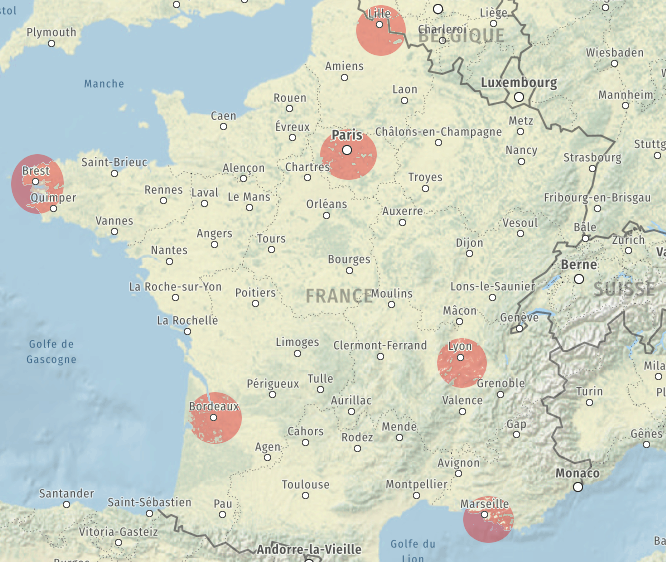
Voici un tableau récapitulant les distances entre ces 6 villes.

	Brest	Bordeaux	Lille	Lyon	Marseille	Paris
Brest	-	598	708	872	1130	572
Bordeaux	598	-	802	520	637	554
Lille	708	802	-	650	1002	225
Lyon	872	520	650	-	367	465
Marseille	1130	637	1002	367	-	777
Paris	572	554	225	465	777	-

Et voici le graphe non orienté et non pondére correspondant :

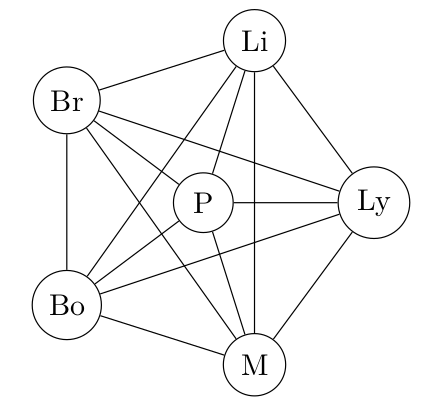
Le problème ? Pour l'instant chaque traversée d'arête "coûte" la même chose ! Mais nous avons vu qu'on pouvait pondérer le coût de la traversée d'une arête. Plaçons donc le kilométrage entre les villes :

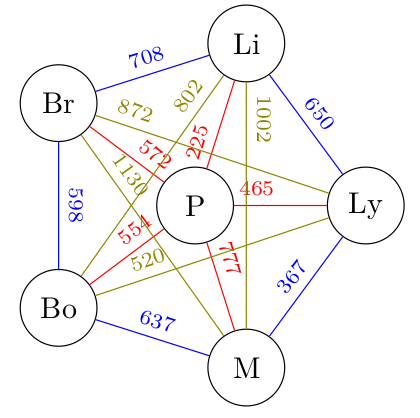
Graphiquement, on a un peu l'impression que c'est le bazar, mais les graphes ne sont pas des objets graphiques : vous avez juste sous les yeux la représentation graphique d'un objet mathématique.

15° Déterminer une matrice d'adjacence de ce graphe pondéré. On prendra 0 pour indiquer qu'on est déjà arrivé (comme lille-lille).

Remarque 1 : pourquoi une matrice ? Tout simplement car il y a ici 6! façons de numéroter les villes.

Remarque 2 : tous les sommets sont reliés. Sinon, il aurait fallu prévoir une valeur encodant "absence d'arête"... Comme le zéro est déjà pris, il reste les nombres négatifs ou Vide ou l'Infini.

Correction ?

...CORRECTION...

J'ai décidé de prendre le même ordre que celui donné dans le tableau. Gain de temps !

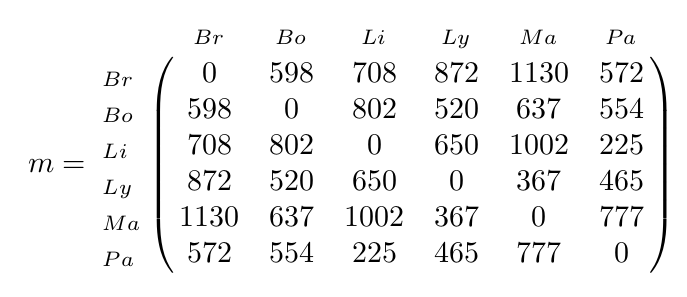
16° Réaliser une représentation graphique du graphe d'un réseau de 4 routeurs fonctionnant en OSPF dont on vous fournit la matrice :

En OSPF, le coût d'une liaison est de 1 (très bon débit ou bande passante) à plus (le débit diminuant lorsque le coût augmente). Un coût de 0 correspond soit au fait qu'on ne sort pas du réseau si on est sur la diagonale, soit une absence de liaison si on ne se trouve pas sur la diagonale.

Remarque : pourquoi une représentation ? Tout simplement car on peut placer les sommets où on veut. Seules les relations sont importantes.

Correction ?

...CORRECTION...

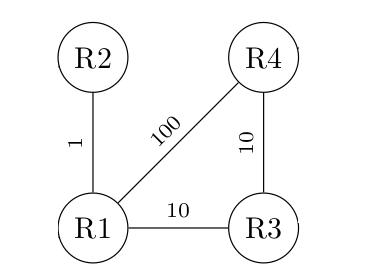
4 - Cas des graphes orientés

⇩ ⇧ ⤊

Reste le cas des graphes orientés. Cette fois, les matrices ne seront plus symétriques, à moins que chaque arc ai son arc complémentaire : (a,b) et (b,a)

Matrice d'adjacence d'un graphe orienté

Nous allons voir qu'on obtient encore des matrices carrées mais qu'elles ne sont pas systématiquement symétriques.

Convention habituelle

On utilise habituellement ce positionnement de l'information. Mais ce n'est qu'une convention : on pourrait très bien prendre l'inverse.

Allure d'une matrice d'un graphe orienté

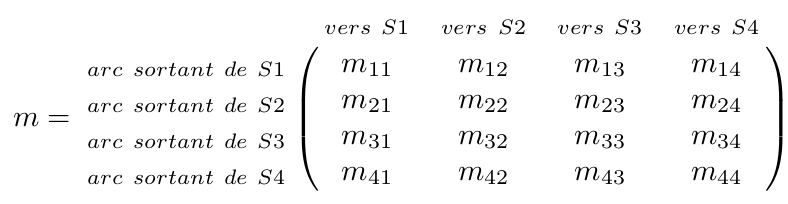
Exemple

Prenons le cas d'un ensemble V pour Vertex ou S de sommets {a, b, c}

L'ensemble A des arcs ou E pour edges disponibles est { (a,b), (a,c), (b,c), (c,a) }.

Il y a donc un arc de a vers b, de a vers c, de b vers c et de c vers a.

Graphiquement, on pourrait obtenir ceci :

le graphe orienté composé des sommets abc

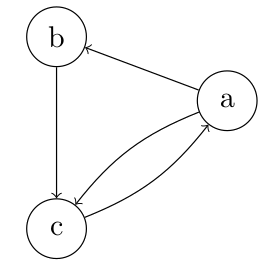
Commençons par décrire la première ligne : celle qui fournit les arcs sortant de a : (a,b) et (a,c).

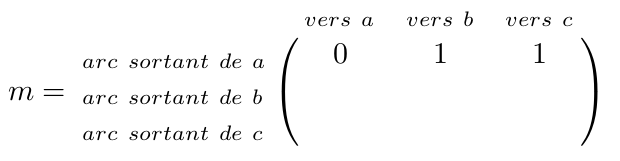
Ensuite, on rajoute le seul arc sortant de b : (b,c).

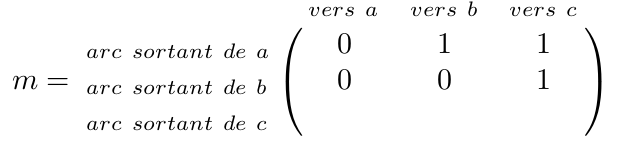
Enfin, on rajoute le seul arc sortant de c : (c,a).

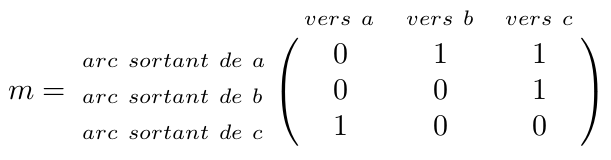
Si on indique ailleurs que a porte le numéro 1, b le 2 et c le 3, on peut la réduire à ceci :

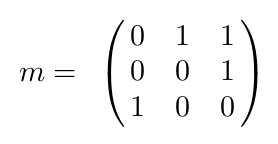
Il s'agit donc bien d'une matrice carré mais non symétrique.

17° Voici le graphe orienté de la succession de vêtements à enfiler pour s'habiller. On se limite ici à chaussettes, chaussures, pantalon et caleçon.

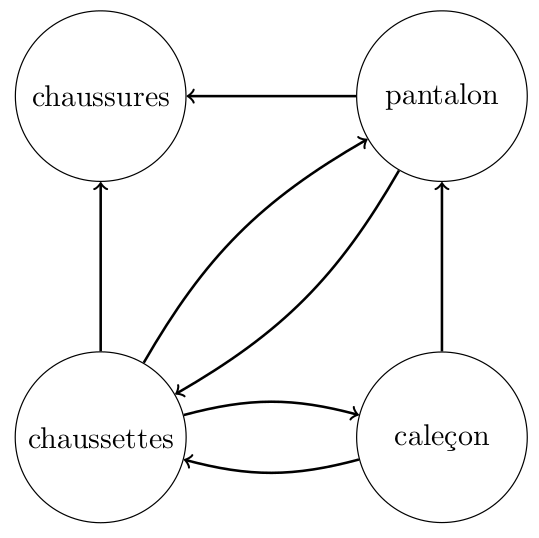
Questions

Donner un chemin pour s'habiller entièrement en partant du caleçon ?
Donner un chemin pour s'habiller entièrement en partant des chaussettes ?
Peut-on s'habiller entièrement en partant des chaussures ?
Fournir la matrice de ce graphe orienté

Correction ?

...CORRECTION...

Quel chemin pour s'habiller entièrement en partant du caleçon ?

caleçon -> pantalon -> chaussettes -> chaussures

caleçon -> chaussettes -> pantalon -> chaussures

Quel chemin pour s'habiller entièrement en partant des chaussettes ?

chaussettes -> caleçon -> pantalon -> chaussures

Peut-on s'habiller entièrement en partant des chaussures ?

Non, pas d'arc sortant : il faut venir par là.

Fournir la matrice de ce graphe non orienté

Les graphes interviennent également dans l'organisation des projets comme vous avez pu le voir avec le cas simple des habits à enfiler dans un certain ordre. Connaître les relations de dépendances d'une partie d'un projet sur une ordre permet d'ordonner correctement les tâches à réaliser. Comme pour construire une maison ou un immeuble par exemple.

5 - Implémentation Python

⇩ ⇧ ⤊

Matrice en tant que tableau de tableaux d'integers

S'agissant d'une matrice, nous avions déjà vu qu'on pouvait utiliser un simple tableau de tableaux.

Exemple - rappel

Imaginons qu'on veuille encoder cette matrice OSPF en mémoire :

Il suffit de créer un tableau par ligne puis de placer les tableaux-lignes dans un autre tableau.

m = [
    [0, 1, 10, 100],
    [1, 0, 0, 0],
    [10, 0, 0, 10],
    [100, 0, 10, 0]
]

Si on veut obtenir les arcs sortants du sommet d'indice 2, il suffit alors de taper ceci : (en se souvenant qu'ici indice 2 veut dire 3e ligne !)


>>> m[2]
[10, 0, 0, 10]

Si on veut avoir le coût de l'arc sortant du routeur d'indice 2 vers le routeur d'indice 3 :


>>> m[2][3]
10

La convention d'utilisation est donc :

nom_matrice[ligne][colonne] ou
nom_matrice[sortant][entrant] ou
nom_matrice[depuis][vers].

A savoir : comme accéder à un élément d'un tableau statique se fait à coût constant, connaître l'état d'un arc quelconque se fait donc à coût constant dans une matrice d'adjacence.

18° La matrice d'adjacence implémentée ci-dessous est-elle symétrique ? Peut-elle encoder un graphe non orienté ? Donner les contenus des variables a et b.

m = [
    [1, 2, 10, 20],
    [1, 6, 0, 8],
    [10, 0, 5, 10],
    [100, 0, 10, 1]
]
 
a = m[1][3]
b = m[3][1]

Correction ?

...CORRECTION...

La matrice n'est pas symétrique puisqu'on ne peut pas écrire m[i][j) = m[j][i] pour n'importe quelle valeur valable d'indice.

Elle ne peut pas représenter un graphe non orienté car la matrice d'un graphe non orienté est nécessairement symétrique.

Si on cherche a, on commence par sélectionner la ligne-tableau d'indice 1 et on recherche son élément d'indice 3.

m = [
    [1, 2, 10, 20],
    [1, 6, 0, 8],
    [10, 0, 5, 10],
    [100, 0, 10, 1]
]
 
a = m[1][3]
b = m[3][1]

Si on cherche b, on commence par sélectionner la ligne-tableau d'indice 3 et on recherche son élément d'indice 1.

m = [
    [1, 2, 10, 20],
    [1, 6, 0, 8],
    [10, 0, 5, 10],
    [100, 0, 10, 1]
]
 
a = m[1][3]
b = m[3][1]

19-programmation° Réaliser les trois fonctions demandées.

Pour nb_arc_sortant(), cela revient à compter les éléments différents de 0 sur la bonne "ligne".

Pour nb_arc_entrant(), cela revient à compter les éléments différents de 0 sur la bonne "colonne".

Pour est_symetrique(), il faut vérifier avec une boucle qu'on vérifie bien mtr[i][j) == mtr[j][i] pour toutes les valeurs possibles de i et j. On notera qu'on peut se limiter aux cas où i >= j. Utilisé dans le cadre d'une fonction de vérification, cela revient à vérifier pour chaque possibilité si mtr[i][j) != mtr[j][i] et sortir en renvoyant False si c'est le cas.

On notera qu'on a choisi ici de réaliser un jeu de tests composé simplement d'assertions plutôt que d'utiliser le module doctest et une documentation d'exemples.

m = [
    [0, 2, 10, 20],
    [2, 6, 0, 8],
    [10, 0, 5, 10],
    [20, 0, 10, 1]
]
 
def nb_arc_sortant(mtr:list, i:int) -> int:
    """Renvoie le nombre d'arcs sortants du noeud d'indice i"""
    pass
 
def nb_arc_entrant(mtr:list, j:int) -> int:
    """Renvoie le nombre d'arcs entrants vers le noeud d'indice j"""
    pass
 
def est_symetrique(mtr:list) -> bool:
    """True si mtr est une matrice symétrique"""
    pass
 
if __name__ == '__main__':
    assert nb_arc_sortant(m, 1) == 3
    assert nb_arc_entrant(m, 1) == 2
    assert est_symetrique(m) == False

Correction ?

...CORRECTION...

m = [
    [0, 2, 10, 20],
    [2, 6, 0, 8],
    [10, 0, 5, 10],
    [20, 0, 10, 1]
]
 
def nb_arc_sortant(mtr:list, i:int) -> int:
    """Renvoie le nombre d'arcs sortants du noeud d'indice i"""
    nb_col = len(mtr[i])  # on récupère le nombre de colonnes sur la ligne numéro i
    nb = 0
    for j in range(nb_col):
        if mtr[i][j] != 0:
            nb = nb + 1
    return nb
 
def nb_arc_entrant(mtr:list, j:int) -> int:
    """Renvoie le nombre d'arcs entrants vers le noeud d'indice j"""
    nb_lig = len(mtr)  # on récupère le nombre de lignes dans la matrice
    nb = 0
    for i in range(nb_lig):
        if mtr[i][j] != 0:
            nb = nb + 1
    return nb
 
def est_symetrique(mtr:list) -> bool:
    """True si mtr est une matrice symétrique"""
    for i in range(len(mtr)):
        for j in range(0, i):
            if mtr[i][j] != mtr[j][i]:
                return False
    return True
 
if __name__ == '__main__':
    assert nb_arc_sortant(m, 1) == 3
    assert nb_arc_entrant(m, 1) == 2
    assert est_symetrique(m) == False

Finissons avec le module networkx associé à matplotlib qui permet facilement de tracer des graphes.

20° Si ce n'est pas encore fait, installer les modules matplotlib et networkx via Gérer les modules de Thonny ou en les installant directement dans Python :

Avec Windows


C:\Users\moi>python -m pip install --user matplotlib
 
C:\Users\moi>python -m pip install --user networkx

Avec un système dérivé d'Unix (Linux ou MacOS) :


rv@rv-HP2:~$ python3 -m pip install --user matplotlib
 
rv@rv-HP2:~$ python3 -m pip install --user networkx

21° Utiliser le programme suivant. Il permet de tracer un graphe non orienté à partir de la matrice d'adjacence qu'on lui transmet ligne 69.

Vous pouvez le lancer plusieurs fois : vous devriez constater que pour une même matrice, le module crée plusieurs représentations différentes.

# 1 - Importations
 
import networkx as nx
import matplotlib.pyplot as plt # pour les représentations graphiques
 
# 2 - Déclaration des fonctions
 
def creer_graphe_non_oriente(noms, m):
    """Crée et renvoie un graphe networkx à partir des informations reçues
 
    :: param noms(list)  :: tableau contenant les étiquettes des sommets
    :: param m(list)     :: matrice d'adjacence SYMETRIQUE CARREE sous la forme tableau de tableau
    :: return (nx.Graph) :: un objet-graphe NON ORIENTE du module networkx
 
    """
    g = nx.Graph()
 
    # Création des sommets
    for nom in noms:
        g.add_node(nom)
 
    # Création des arêtes
    for i in range(len(m)):
        for j in range(i+1):  # on profite que m soit symétrique
            if m[i][j] != 0:
                a = noms[i]  # étiquette du premier sommet
                b = noms[j]  # étiquette du deuxième sommet
                g.add_edge(a,b)
                g[a][b]['weight'] = m[i][j]
 
    return g
 
def tracer_graphe_non_oriente(g, couleurs, m):
    """Trace un graphe à partir des informations reçues
 
    :: param g(nx.Graph)    :: un objet-graphe NON ORIENTE du module networkx
    :: param couleurs(list) :: tableau contenant les couleurs des sommets    
    :: param m(list)        :: matrice d'adjacence SYMETRIQUE CARREE sous la forme tableau de tableau
 
    """
 
    pos = nx.spring_layout(g)  # on récupère les positions graphiques des sommets
    poids = nx.get_edge_attributes(g, 'weight')  # on récupère le poids des arêtes
 
    # On trace les noeuds (alpha pour la transparence)
    nx.draw_networkx_nodes(g, pos, node_size=700,
        node_color=couleurs, alpha=0.7)
 
    # On note les étiquettes sur les noeuds
    nx.draw_networkx_labels(g, pos, font_size=12,
        font_color='black', font_family='sans-serif')
 
    # On trace les arêtes
    nx.draw_networkx_edges(g, pos, width=2.0)
 
    # On note les poids sur les arêtes
    nx.draw_networkx_edge_labels(g, pos, edge_labels=poids)
 
    plt.savefig("mon_graphe.png") # permet de le sauvegarder automatiquement 
    plt.show()  # on affiche le graphique à l'écran
 
 
# 3 - Programme de test : création et visualiation d'un graphe non orienté
 
if __name__ == '__main__':
 
    n1 = ["R1", "R2", "R3", "R4"]  # Noms-étiquettes des sommets
    c1 = ["red", "blue", "green", "orange"]  # Couleurs attribuées aux sommets
    m1 = [
        [0, 2, 10, 20],
        [2, 0, 0, 8],
        [10, 0, 0, 10],
        [20, 8, 10, 0]
    ]
 
    g1 = creer_graphe_non_oriente(n1, m1)
    tracer_graphe_non_oriente(g1, c1, m1)

Et voilà, vous devriez voir apparaître un graphe sur votre écran.

Exemples : VOIR résultat 1 ou VOIR résultat 2

Si vous voulez tracer un graphe orienté à partir de sa matrice d'adjacence, il faudra utiliser le programme ci-dessous. On n'utilise plus le constructeur Graph mais le constructeur DiGraph, comme Directed Graph, graphe orienté en anglais.

22° Utiliser le programme suivant. Il permet de tracer un graphe orienté à partir d'une matrice d'adjacence qu'on lui transmet.

Vous pouvez le lancer plusieurs fois : vous devriez constater que pour une même matrice, le module crée plusieurs représentations différentes.

Remarque : j'ai commenté la partie où on rajoute les poids sur les arcs car le module ne les place pas facilement au bon endroit lorsqu'on utilise l'option arc arrondi.

# 1 - Importations
 
import networkx as nx
import matplotlib.pyplot as plt # pour les représentations graphiques
 
# 2 - Déclaration des fonctions
 
def creer_graphe_oriente(noms, m):
    """Crée et renvoie un graphe networkx à partir des informations reçues
 
    :: param noms(list)  :: tableau contenant les étiquettes des sommets
    :: param m(list)     :: matrice d'adjacence CARREEE sous la forme tableau de tableau
    :: return (DiGraph)  :: un objet-graphe ORIENTE du module networkx
 
    """
    g = nx.DiGraph()
 
    # Création des sommets
    for nom in noms:
        g.add_node(nom)
 
    # Création des arêtes
    for i in range(len(m)):
        for j in range(len(m)):  # on profite que m soit carrée
            if m[i][j] != 0:
                a = noms[i]  # étiquette du premier sommet
                b = noms[j]  # étiquette du deuxième sommet
                g.add_edge(a,b)
                g[a][b]['weight'] = m[i][j]
 
    return g
 
def tracer_graphe_oriente(g, couleurs, m):
    """Trace un graphe à partir des informations reçues
 
    :: param g (nx.DiGraph) :: un objet-graphe ORIENTE du module networkx
    :: param couleurs(list) :: tableau contenant les couleurs des sommets    
    :: param m(list)        :: matrice d'adjacence CARREE sous la forme tableau de tableau
 
    """
 
    pos = nx.spring_layout(g)  # on récupère les positions graphiques des sommets
    poids = nx.get_edge_attributes(g, 'weight')  # on récupère le poids des arêtes
 
    # On trace les noeuds
    nx.draw_networkx_nodes(g, pos, node_size=700,
        node_color=couleurs, alpha=0.7)
 
    # On note les étiquettes sur les noeuds
    nx.draw_networkx_labels(g, pos, font_size=12,
        font_color='black', font_family='sans-serif')
 
    # On rajoute les arcs
    nx.draw_networkx_edges(g2, pos, width=2.0,
        arrowsize=20, connectionstyle='arc3,rad=0.2')
 
    # On note les poids sur les arcs
    #nx.draw_networkx_edge_labels(g2, pos, edge_labels=poids,
    #    horizontalalignment='left', label_pos=0.5)
 
    plt.savefig("mon_graphe.png") # permet de le sauvegarder automatiquement 
    plt.show()  # on affiche le graphique à l'écran
 
 
# 3 - Programme de test : création et visualiation d'un graphe non orienté
 
if __name__ == '__main__':
 
    n2 = ["R1", "R2", "R3", "R4"]  # Noms-étiquettes des sommets
    c2 = ["red", "blue", "green", "orange"]  # Couleurs attribuées aux sommets
    m2 = [
        [0, 2, 0, 20],
        [2, 0, 0, 8],
        [10, 0, 0, 10],
        [0, 0, 10, 0]
    ]
 
    g2 = creer_graphe_oriente(n2, m2)
    tracer_graphe_oriente(g2, c2, m2)

Et voilà, vous devriez voir apparaître un graphe orienté sur votre écran.

Exemples : VOIR résultat 3 ou VOIR résultat 4

Nous verrons peut-être plus tard comment placer précisement les éléments si vous trouvez que leurs positions ne conviennent pas. Tout se passe dans le dictionnaire pos.

Avantages et désavantages de la matrice d'adjacence

Avantages

Simple à utiliser
Savoir si un arc ou une arête existe est une action à coût constant (Θ(1))

Désavantages

Place mémoire dont le coût est quadratique (Θ(n²)), n étant le nombre de sommets, la taille du graphe. En réalité, on pourrait faire mieux si on utilise un octet pour représenter 8 arêtes. On garde néanmoins un coût quadratique...
Enumérer les arcs sortant d'un sommet est à coût linéaire (Θ(n)) même si la matrice est peu dense : il faut lire toutes les colonnes (alors qu'elles contiennent surtout des 0...)

6 - FAQ

⇩ ⇧ ⤊

Mais on stocke comment les données sur les sommets ?

Il est vrai que cette activité traite surtout de l'encodage des relations entre les sommets.

Pour les sommets, c'est un peu comme les noeuds des arbres. Il y a autant de façons de faire qu'on veut.

Prenons l'exemple d'un célèbre jeu de rôle où on doit tuer des dragons dans un donjon. Voici le plan d'un petit donjon.

Matrice exemple pour la liste d'adjacence

Nous pourrions utiliser des tuples où l'indice 0 serait l'étiquette et l'indice 1 un autre tuple qui contiendrait les informations sur la salle :

# Création des sommets avec un tuple contenant un string et un tableau
 
a = ("A", ("Salle de garde", 6, "Gobelin", 100))
b = ("B", ("Antre du Dragon", 1, "Dragon", 2000))
c = ("C", ("Crypte", 3, "Zombie", 200))
d = ("D", ("Salle secrête", 3, "Araignée Géante", 1000))
 
tresor_en_salle_a = a[1][3]

Nous pourrions utiliser des dictionnaires où chaque clé correspondrait à une information sur le sommet ou la salle :

# Création des sommets avec des dictionnaires
 
a = {"etiquette": "A", "nom": "Salle de garde", "nb": 6, "monstre": "Gobelin", "tresor": 100}
b = {"etiquette": "B", "nom": "Antre du Dragon", "nb": 1, "monstre": "Dragon", "tresor": 2000}
c = {"etiquette": "C", "nom": "Crypte", "nb": 3, "monstre": "Zombie", "tresor": 200}
d = {"etiquette": "D", "nom": "Salle secrête", "nb": 3, "monstre": "Araignée Géante", "tresor": 1000}
 
tresor_en_salle_b = b["tresor"]

Nous pourrions utiliser des objets où chaque attribut correspondrait à une information sur le sommet ou la salle :

# Création des sommets avec des objets
 
class Salle:
    def __init__(self, e, n, nb, m, t):
        self.etiquette = e
        self.nom = n
        self.nb = nb
        self.monstre = m
        self.tresor = t
 
a = Salle("A", "Salle de garde", 6, "Gobelin", 100)
b = Salle("B", "Antre du Dragon", 1, "Dragon", 2000)
c = Salle("C", "Crypte", 3, "Zombie", 200)
d = Salle("D", "Salle secrête", 3, "Araignée Géante", 1000)
 
tresor_en_salle_c = c.tresor

Activité publiée le 30 03 2021
Dernière modification : 07 04 2021
Auteur : ows. h.

⏪

⏫

⏩