1 - Exercices Binaire
Fiche d'exercices totalement corrigés.
01° Donnez les poids respectifs des 8 bits d'un octet. Vous commencerez par le bit de poids fort.
| Bit n° | n°7(fort) | n°6 | n°5 | n°4 | n°3 | n°2 | n°1 | n°0(faible) |
| Les bits codent | ? | ? | ? | ? | ? | ? | ? | ? |
...REPONSE ATTENDUE...
| Bit n° | n°7(fort) | n°6 | n°5 | n°4 | n°3 | n°2 | n°1 | n°0(faible) |
| Les bits codent | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
02° Donnez en le justifiant la valeur en base 10 du nombre exprimé en base 2 :
N = 0001 1100 2.
...REPONSE ATTENDUE...
28
En effet, on active ici les bits de points 16, 8 et 4. On obtient N = 16 + 8 + 4.
03° Donnez en le justifiant la valeur en base 10 du nombre nombre exprimé en base 2 :
N = 1111 1111 2.
...REPONSE ATTENDUE...
On active tous les bits de l'octet.
N = 255.
En effet, on a N = 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1.
04° Combien de cas différents peut-on encoder avec 8 bits ? Est-ce cohérent avec la réponse à la question 03 ?
...REPONSE ATTENDUE...
On sait que le nombre de combinaisons possibles est 28.
Or puisque la première valeur est 0, on ne peut aller que jusqu'à 255.
C'est donc cohérent avec le calcul précédent.
05° Trouver la représentation binaire de 135 en utilisant la méthode de l'activation progressive.
...REPONSE ATTENDUE...
Pour encoder 135 :
- On active le bit 128.
- Il reste alors à encoder (135-128), soit 7.
- On active le bit 4.
- Il reste alors à encoder (7-4), soit 3.
- On active le bit 2.
- Il reste alors à encoder (3-2), soit 1.
- On active le bit 1.
- C'est fini.
N = 1000 0111 2.
06° Trouver la représentation binaire de 42 en utilisant la méthode de l'activation progressive.
...REPONSE ATTENDUE...
Pour encoder 42 :
- On active le bit 32.
- Il reste alors à encoder (42-32), soit 10.
- On active le bit 8.
- Il reste alors à encoder (10-8), soit 2.
- On active le bit 2.
- C'est fini.
N = 0010 1010 2.
07° Trouver la représentation binaire de 135 en utilisant la méthode de la division par 2.
...REPONSE ATTENDUE...
On divise par deux de façon euclidienne jusqu'à obtenir un quotient de 0.
La décomposition est alors l'ensemble des restes mais attention : le bit de poids fort est le bit du bas.
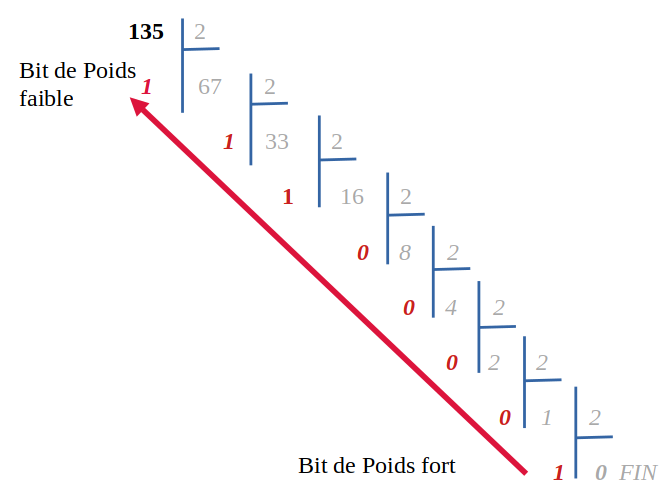
N = 1000 0111 2.
08° Trouver la représentation binaire de 42 en utilisant la méthode de la division par 2.
...REPONSE ATTENDUE...
On divise par deux de façon euclidienne jusqu'à obtenir un quotient de 0.
La décomposition est alors l'ensemble des restes mais attention : le bit de poids fort est le bit du bas.
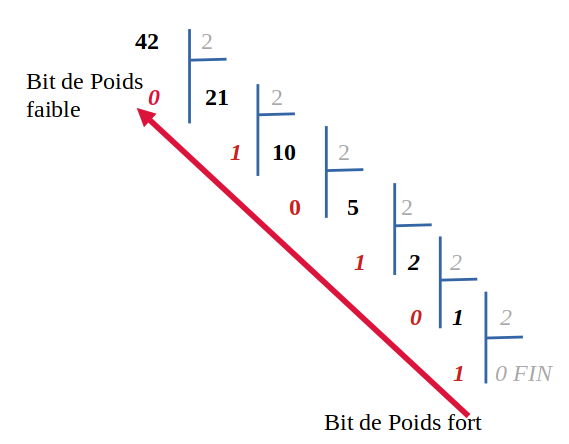
N = 10 1010 2.
09° Convertir une mémoire mem de 850 Mo en ko puis en Go.
...REPONSE ATTENDUE...
mem = 850 Mo = 850000 ko = 0.850 Go
10° Convertir 60 Go en Mo puis en ko.
...REPONSE ATTENDUE...
mem = 60 Go = 60000 Mo = 60000000 ko.
11° Combien de bits pour former un octet ? Quelle est le nombre de valeurs disponibles ? Quelle est la plus petite valeur ? Quelle est la plus grande valeur ?
...REPONSE ATTENDUE...
8 bits pour former un octet.
Il y a 28 possibilités, ce qui donne 256 valeurs.
La plus petite est N = 0 = 0000 0000 2
La plus grande est N = 255 = 1111 1111 2
Activité publiée le 13 09 2020
Dernière modification : 13 09 2020
Auteur : ows. h.