35 - Récursivité avec Python
La récursivité est un moyen efficace et intuitif de programmer. Elle est très courante même si nous n'en avons pas encore parlé car elle nécessite d'avoir des connaissances assez précises des fonctions pour en comprendre réellement le fonctionnement.
Ca tombe bien : c'est maintenant votre cas.
Prérequis : les activités précédentes sur les fonctions
Logiciel nécessaire pour l'activité : Python 3 : Thonny, IDLE ...
Documents de cours PDF : .PDF
Sources latex : .TEX et entete.tex et licence.tex
Evaluation : 8 questions
✎ question 13-14-15-16-17-18-19
✌ question 20
DM 🏠 : oui
Résumé : Version HTML ou fond blanc ou ou PDF (couleur ou gris)
1 - Découverte du principe
01° Utiliser le code ci-dessous pour répondre à ces questions ou ces actions :
- Sans lancer le programme, écrire ce qu'il va afficher à l'écran à votre avis.
- Lancer le programme pour visualiser le résultat réel
- Fournir enfin les lignes suivies par l'interpréteur pendant l'exécution de la demande.
1
2
3
4
5
6
7 | |
...CORRECTION...
On crée une boucle bornée partant de 5, décroissante avec un pas de -1 et dont la borne limite exclue est -1. x varie donc de 5 à 0.
Appel de p(5)
Appel de p(4)
Appel de p(3)
Appel de p(2)
Appel de p(1)
Appel de p(0)
Pour le déroulé :
- L1 : définition (mise en mémoire) de la fonction p()
- L6 Tour de boucle avec x=5 - L7(appel) - L1(réception du 5) - L3 (affichage) - L4 (réponse) - L7(retour)
- L6 Tour de boucle avec x=4 - L7(appel) - L1(réception du 4) - L3 (affichage) - L4 (réponse) - L7(retour)
- L6 Tour de boucle avec x=3 - L7(appel) - L1(réception du 3) - L3 (affichage) - L4 (réponse) - L7(retour)
- L6 Tour de boucle avec x=2 - L7(appel) - L1(réception du 2) - L3 (affichage) - L4 (réponse) - L7(retour)
- L6 Tour de boucle avec x=1 - L7(appel) - L1(réception du 1) - L3 (affichage) - L4 (réponse) - L7(retour)
- L6 Tour de boucle avec x=0 - L7(appel) - L1(réception du 0) - L3 (affichage) - L4 (réponse) - L7(retour)
- Fin (pas de ligne 8)
Ce type de fonctionnement correspond à un fonctionnement itératif : lorsqu'une fonction f() (ou un programme comme ici) doit répondre à un demande et qu'elle dispose de trois autres fonctions a() b() c() pour l'aider, c'est f() qui fait presque tout le travail :
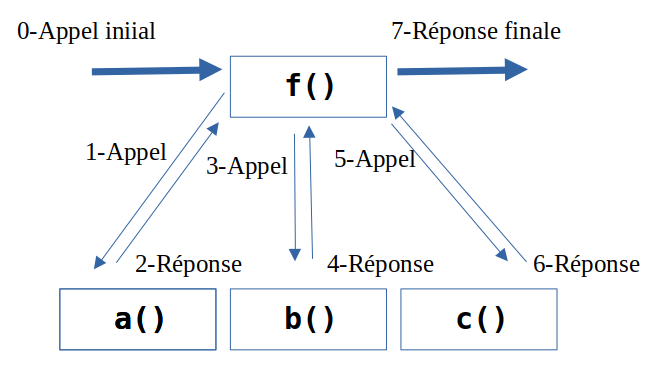
- f() reçoit la demande puis
- f() fait appel à a(), attend et stocke sa réponse puis
- f() fait appel à b(), attend et stocke sa réponse puis
- f() fait appel à c(), attend et stocke sa réponse puis
- f() utilise les trois sous-réponses pour construire la réponse globale et répond à la demande.
Mais nous pouvons faire la même chose avec un appel récursif : la fonction peut alors faire appel à une autre instance d'elle-même (une nouvelle version d'elle-même).
02° Utiliser le code ci-dessous pour répondre à ces questions ou ces actions :
- Que répond une fonction Python qui a fini son exécution sans rencontrer de return ?
- Quel va être le premier affichage sur la console ?
- Le programme va-t-il s'arrêter ou va-t-on lancer un nouvel appel ?
- Quel appel ?
- Que va-t-il afficher ? Que va-t-il activer ?
- Sans lancer le programme, écrire ce qu'il va afficher à l'écran à votre avis.
- Lancer le programme pour visualiser le résultat réel
- Fournir enfin les lignes suivies par l'interpréteur pendant l'exécution de la demande.
1
2
3
4
5
6
7
8
9 | |
...CORRECTION...
On lance l'appel p(5). Cela va provoquer via la ligne 3 l'affichage suivant :
Appel de p(5)
Comme x référence 5, on va en ligne 7.
On lance alors l'appel p(4). Cela va provoquer via la ligne 3 l'affichage suivant :
Appel de p(4)
Comme x référence 4, on va en ligne 7.
On lance alors l'appel p(3). Cela va provoquer via la ligne 3 l'affichage suivant :
Appel de p(3)
Comme x référence 3, on va en ligne 7.
On lance alors l'appel p(2). Cela va provoquer via la ligne 3 l'affichage suivant :
Appel de p(2)
Comme x référence 2, on va en ligne 7.
On lance alors l'appel p(1). Cela va provoquer via la ligne 3 l'affichage suivant :
Appel de p(1)
Comme x référence 1, on va en ligne 7.
On lance alors l'appel p(0). Cela va provoquer via la ligne 3 l'affichage suivant :
Appel de p(0)
Comme x référence 0, on ne relance plus d'appel.
Les lignes de code suivies par l'interpréteur
- L1 (définition de p())
- L9 (appel à p(5)) - L1(réception de 5) - L3 - L4 - L6 - ...
- L7 (appel à p(4)) - L1(réception de 4) - L3 - L4 - L6 - ...
- L7 (appel à p(3)) - L1(réception de 3) - L3 - L4 - L6 - ...
- L7 (appel à p(2)) - L1(réception de 2) - L3 - L4 - L6 - ...
- L7 (appel à p(1)) - L1(réception de 1) - L3 - L4 - L6 - ...
- L7 (appel à p(0)) - L1(réception de 0) - L3 - L4 - L5 - L7 (retour de la réponse None de p(0) à p(1))
- L7 (retour de la réponse None de p(1) à p(2))
- L7 (retour de la réponse None de p(2) à p(3))
- L7 (retour de la réponse None de p(3) à p(4))
- L7 (retour de la réponse None de p(4) à p(2))
- L9 (retour de la réponse None de p(5)
- Pas de L10 : fin du programme.
03° Lancer le programme sur Python Tutor pour comparer à votre lecture du code.
Combien de versions de la fonction sont actives en même temps au maximum : 1 ou 5 ?
Le schéma de principe du fonctionnement récursif pour réaliser les appels est donc différents du cas itératif :
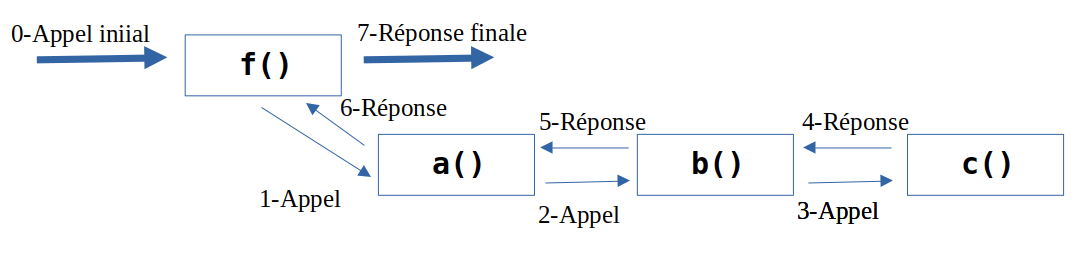
- f() reçoit la demande puis
- f() fait appel à a() et attend la réponse gentillement. Pendant ce temps
- a() fait appel à b() et attend la réponse gentillement. Pendant ce temps
- b() fait appel à c(), et attend la réponse gentillement. Pendant ce temps
- c() travaille et répond à b().
- b() utilise cette réponse pour construire sa propre réponse qu'elle envoie à a().
- a() utilise cette réponse pour construire sa propre réponse qu'elle envoie à f().
- f() utilise cette réponse pour construire la réponse globale et répond à la demande.
il est nécessaire lors de l'utilisation de la récursivité d'avoir une condition d'arrêt qui mène à un cas de base : un cas qui ne provoque pas d'appels récursifs. Sans lui, on lancerait des appels à l'infini.
Ici, la condition d'arrêt est donc x == 0 (ligne 4) puisque cette expression évaluée à True ne provoque pas de nouvel appel à p().
1
2
3
4
5
6
7
8
9 | |
04° Les lignes 4 et 5 sont-elles vraiment nécessaires ici ? Comment pourrait-on écrire cette fonction avec un test IF sans ELSE ?
...CORRECTION...
Non. Elles permettent juste de bien comprendre et montrer qu'il y a deux cas :
- Le cas de base, non récursif
- Le cas récursif : on fait encore appel à la fonction ou la procédure
1
2
3
4
5
6
7 | |
05° Expliquer le problème qu'on va rencontrer sur cette fonction après avoir analysé ce nouveau programme. Il y a un problème. Cherchez bien.
1
2
3
4
5
6
7
8
9 | |
...CORRECTION...
La récursivité provoque une boucle infinie : on ne pourra jamais atteindre la condition d'arrêt puisque les paramètres x deviennent de plus en plus grands. On ne pourra donc jamais valider la condition x == 0.
06° Même question.
1
2
3
4
5
6
7
8
9 | |
...CORRECTION...
La récursivité provoque une boucle infinie : on ne pourra jamais atteindre le cas de base non-recursif puisque le paramètre x vaut successivement 5, 3, 1, -1, -3...
Encore une fois, on ne parviendra pas à s'arrêter.
Pour l'instant, nous n'avons utilisé que des "procédures", des fonctions qui ne renvoient rien. Il s'agit donc d'une simple succession d'action, pas d'un calcul mémorisé.
Voyons un premier exemple classique : le calcul des séries arithmétiques, rencontrées dans la partie Algorithmique.
Pour rappel, voici la formule permettant de calculer la série arithmétique des nombres de 1 à n :
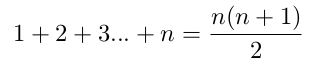
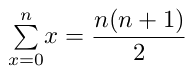formule 107° Réaliser une fonction non récursive permettant de calculer cette série, sans utiliser la formule. Il faut imposer à votre fonction de calculer 1 + 2 + 3 + ... jusqu'à n.
On notera que la fonction fournie possède déjà :
- Une documentation pouvant servir au module doctest.
- Deux assertions permettant d'imposer la précondition sur le paramètre n qui doit être entier et strictement positif.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26 | |
...CORRECTION...
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29 | |
On voit qu'il y a une grande différence entre le code informatique permettant de calculer cette série (boucle et variable de stockage) et sa définition mathématique (une simple addition 1 + 2 +3 + 4 + ...).
La programmation récursive va nous permettre d'obtenir un code qui se rapproche de la version mathématique.
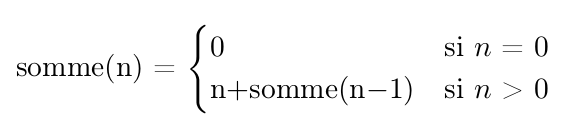
Si on utilise cette définition, on doit alors réfléchir de cette façon :
f(5) = 5 + f(4)
f(5) = 5 + 4 + f(3)
f(5) = 5 + 4 + 3 + f(2)
f(5) = 5 + 4 + 3 + 2 + f(1)
f(5) = 5 + 4 + 3 + 2 + 1 + f(0)
f(5) = 5 + 4 + 3 + 2 + 1 + 0
EN GROUPE° Appliquer l'algorithme suivant applicable à un humain.
- Si on vous demande serie(n) avec n = 1, vous pouvez répondre 1 à la personne qui vous a contacté.
- Sinon si vous êtes le dernier de la liste, vous pouvez calculer directement le résultat puis répondre à la personne qui vous a contacté.
- Sinon, c'est le cas récursif :
- Vous lancez la demande serie(n-1) à la personne suivante et vous attendez qu'elle réponde un jour.
- Une fois que vous connaissez sa réponse, il vous suffit de répondre n + réponse à la personne qui a fait appel à vous.
08° Analyser la fonction récursive. Comparer son code à la version récursive de la somme des n premiers entiers.
Questions :
- pourquoi est-ce bien une fonction et pas une simple procédure ?
- quelle est la version la plus proche de la version mathématique : la fonction itérative ou la fonction récursive ?
1
2
3
4
5
6
7
8
9 | |
Le résultat des appels dans la console affiche encore l'activation progressive des fonctions.
...CORRECTION...
Il s'agit bien d'une fonction car cette fois on renvoie un résultat.
On voit bien que c'est cette version récursive qui se rapproche le plus de la définition mathématique précédente. Plus de variable temporaire à créer. On a bien uniquement les deux cas : le cas de base et le cas itératif.
1 - Fonction récursive
Une fonction récursive est une fonction qui peut lancer un appel à une autre instance d'elle même.
Elle doit posséder au moins deux modes de calcul :
- Un cas récursif où on a besoin de lancer à autre appel à la fonction (en modifiant éventuellement les paramètres d'appel)
- Un cas de base non récursif qui permet d'obtenir une possibilité d'arrêt. On obtient ce cas lorsque la condition d'arrêt est validée. Il faut être vigilant sur cette condition d'arrêt : elle doit pouvoir être atteinte, sinon on obtient une boucle infinie d'appels récursifs.
Exemple : si la réponse de f(5) est return 5 + f(4), alors f(5) doit attendre que f(4) réponde pour évaluer sa propre réponse. Tant que f(4) ne répond pas, f(5) est bloquée et en attente.
EN GROUPE° Appliquer l'algorithme suivant applicable à un humain.
Nouvelle tâche : "Quelle est la taille de la personne la plus grande du groupe" ?
- Si vous êtes le dernier de la liste (cas de base): vous répondez en transmettant votre taille à la personne qui a fait appel à vous.
- Sinon, c'est le cas récursif :
- Vous posez la question à la personne suivante et vous attendez sa réponse
- Une fois que vous connaissez sa réponse, vous sélectionnez la plus grande valeur entre sa réponse et votre propre taille. Vous pouvez alors répondre cette valeur maximum à la personne qui a fait appel à vous.
EN GROUPE° Appliquer l'algorithme suivant applicable à un humain.
Nouvelle tâche : "Quelqu'un a t-il mangé de la pizza hier" ?
- Si vous avez mangé de la pizza hier (cas de base), vous pouvez répondre OUI à la personne qui a fait appel à vous.
- Sinon si vous êtes le dernier (autre cas de base), vous pouvez répondre NON à la personne qui a fait appel à vous.
- Sinon, c'est le cas récursif :
- Vous posez la question à la personne suivante et vous attendez sa réponse
- Une fois que vous connaissez sa réponse, vous n'avez plus qu'à transmettre cette réponse à la personne qui a fait appel à vous.
2 - Empilement et dépilement
Maintenant que vous avez compris le déroulement global d'une fonction récursive, regardons comment fait l'ordinateur concrétement pour réaliser ce calcul.
Regardons à nouveau notre fonction.
1
2
3
4
5
6
7
8
9 | |
Lors de l'appel à f(5), on voit donc que la fonction va devoir renvoyer 5 + f(4). Pour faire cela, elle va donc devoir attendre la réponse de f(4).
09° La fonction f(5) peut-elle renvoyer directement un résultat au programme qui l'a appelé ou doit-elle d'abord calculer quelque chose ?
...CORRECTION...
On constate bien que la fonction ne peut rien renvoyer pour l'instant : elle doit renvoyer 5 + f(4) mais ne connait pas le résulat de f(4).
Avant de renvoyer le résultat de f(5) au programme principal, il va donc falloir renvoyer le résultat de f(4) à f(5).
10° Observer le déroulement du programme sur le site Python Tutor, ou utiliser le mode DEBUG progressif de Thonny si vous ne parvenez pas à aller sur Python Tutor.
Vous devriez avoir visualisé le déroulement progressif du calcul :
- Le programme principal active f(5). Cette fonction veut renvoyer 5 + f(4). On met donc cette fonction f(5) en pause et on lance f(4). Pour répondre f(5) devra attendre la réponse de f(4).
- Cette fonction f(4) veut renvoyer 4 + f(3). On met donc cette fonction f(4) en pause et on lance f(3).
- Cette fonction f(3) veut renvoyer 3 + f(2). On met donc cette fonction f(3) en pause et on lance f(2).
- Cette fonction f(2) veut renvoyer 2 + f(1). On met donc cette fonction f(2) en pause et on lance f(1).
- Cette fonction f(1) veut renvoyer 1 + f(0). On met donc cette fonction f(1) en pause et on lance f(0).
- Cette fonction f(1) peut enfin répondre sans attendre et va renvoyer 0. C'est le cas de base.
Mais, au fait, comment est-ce que ça fonctionne ? Comment une fonction sait à qui répondre une fois qu'elle a fini son travail ?
2 - Culture générale : pile d'exécution, call stack en anglais
La pile d'exécution est la structure de données dans laquelle on enregistre les informations sur les appels de fonctions dans un programme informatique. C'est grace à elle qu'on sait "qui appelle qui" et quelle réponse donner à qui.
Sans rentrer dans les détails, on va donc empiler des blocs d'informations à partir d'une adresse de départ.
Chacun appel de fonction génère son bloc de données.
Chaque bloc contient notamment :
- l'adresse à laquelle le return doit renvoyer la réponse (le bloc du dessous normalement)
- Les paramètres enregistrés lors de l'appel
- les variables locales qu'elle utilise lors de son exécution
Si nous simplifions la notion pour n'en garder que ce qui nous intéresse aujourd'hui, voici le contenu de la pile au fur et à mesure de l'exécution de notre fonction f(5)
.On commence avec f(5) qui demande l'appel de f(4)
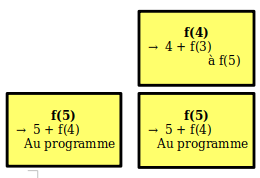
Ensuite f(4) demande l'appel de f(3)
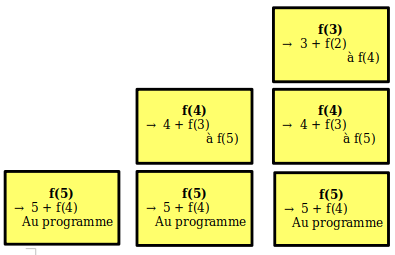
On continue avec f(3) demande l'appel de f(2)
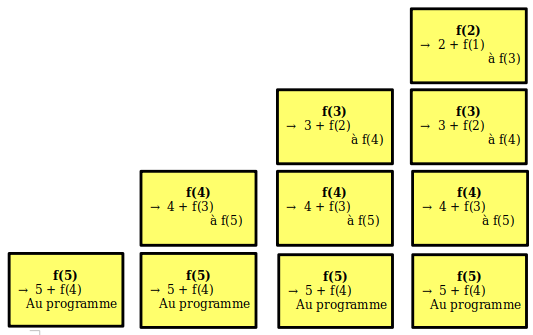
Et, nous allons accumuler sur cette pile, les appels récursifs jusqu'à arriver à la condition d'arrêt. Ici, elle apparaît lors de l'appel à f(0).
Voici la pile d'exécution lorsqu'on en arrive là :
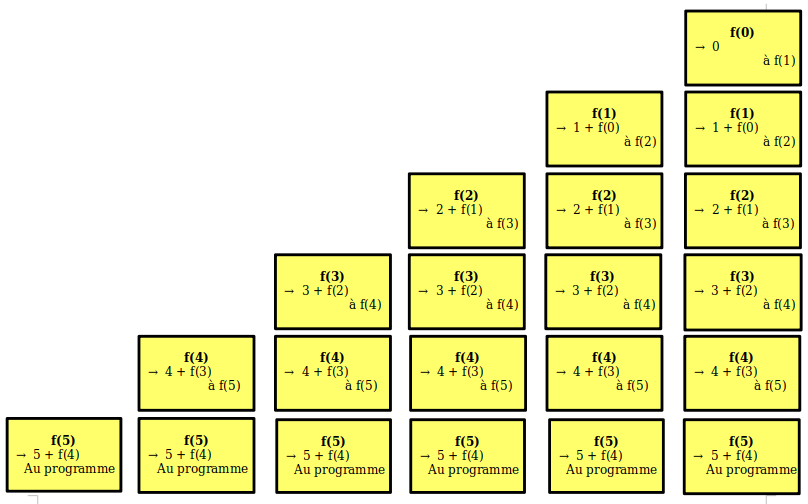
En anglais, on dira call stack.
11° Continuer sur une feuille cette autre représentation des appels successifs imbriqués les uns dans les autres.
f(5) va renvoyer 5 + f(4)
|
va renvoyer 4 + f(3)
|
...CORRECTION...
f(5) renvoie 5 + f(4)
|
va renvoyer 4 + f(3)
|
va renvoyer 3 + f(2)
|
va renvoyer 2 + f(1)
|
va renvoyer 1 + f(0)
|
renvoie 0
12° Continuer cette dernière représentation des appels successifs imbriqués les uns dans les autres.
Appel à f(5) va renvoyer 5 + f(4)
Appel à f(4) va renvoyer 4 + f(3)
Appel à ...
...CORRECTION...
Appel à f(5) va renvoyer 5 + f(4)
Appel à f(4) va renvoyer 4 + f(3)
Appel à f(3) va renvoyer 3 + f(2)
Appel à f(2) va renvoyer 2 + f(1)
Appel à f(1) va renvoyer 1 + f(0)
Appel à f(0) renvoie 0
3 - Dépilement
Une fois le cas de base atteint, on ne rajoute plus rien sur la pile.
On peut maintenant calculer les réponses à renvoyer aux fonctions ayant lancé les appels pour qu'elles puissent évaluer leurs propres réponses.
Nous venons de voir que f(0) renvoie 0 à f(1).
Donc f(1) renvoie 1+0 et donc 1 à f(2).
Donc f(2) renvoie 2+1 et donc 3 à f(3).
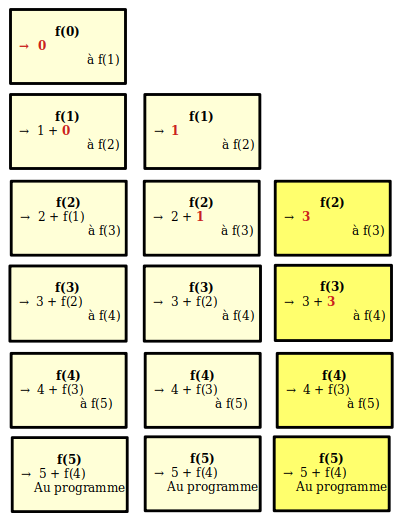
Donc f(3) renvoie 3+3 et donc 6 à f(4).
Donc f(4) renvoie 4+6 et donc 10 à f(5).
Enfin f(5) renvoie 5+10 et donc 15 au programme qui en a fait initialement appel.
Et voilà donc le schéma global de l'empilement et du dépilement :
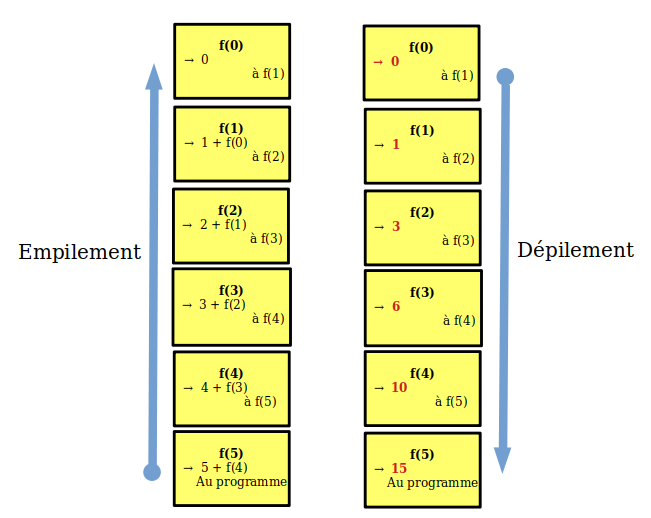
✎ 13° Expliquer la réponse obtenue après dépilement en utilisant cette autre représentation de l'empilement.
f(5) renvoie 5 + f(4)
|
renvoie 4 + f(3)
|
renvoie 3 + f(2)
|
renvoie 2 + f(1)
|
renvoie 1 + f(0)
|
renvoie 0
✎ 14° Expliquer la réponse obtenue après dépilement en utilisant cette autre représentation de l'empilement.
Appel à f(5) renvoie 5 + f(4)
Appel à f(4) renvoie 4 + f(3)
Appel à f(3) renvoie 3 + f(2)
Appel à f(2) renvoie 2 + f(1)
Appel à f(1) renvoie 1 + f(0)
Appel à f(0) renvoie 0
Si on met bout à bout l'empilement des appels jusqu'à atteindre le cas de base puis le dépilement au fur et à mesure de la réception des réponses, on obtient ceci :
Appel à f(5) va renvoyer 5 + f(4) Début de l'empilement
Appel à f(4) va renvoyer 4 + f(3) ⇩
Appel à f(3) va renvoyer 3 + f(2) ⇩
Appel à f(2) va renvoyer 2 + f(1) ⇩
Appel à f(1) va renvoyer 1 + f(0) ⇩
Appel à f(0) renvoie 0 Cas de base
Appel à f(1) renvoie 1 + 0 = 1 ⇩
Appel à f(2) renvoie 2 + 1 = 3 ⇩
Appel à f(3) renvoie 3 + 3 = 6 ⇩
Appel à f(4) renvoie 4 + 6 = 10 ⇩
Appel à f(5) renvoie 5 + 10 = 15 Fin du dépilement
4 - Exercices de programmation
Voyons maintenant si vous parvenez à réaliser vous-mêmes quelques fonctions récursives, simples ou pas.
✎ 15° Réaliser une fonction produit() récursive correspondant à cette manière de voir la multiplication : 5 * 6 = 5+5+5+5+5+5.
Attention aux spécifications d'entrée : n et p sont des entiers, p étant positif.
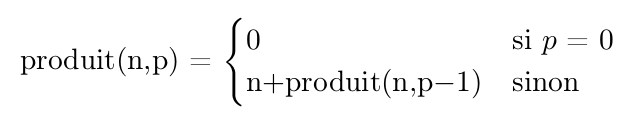
✎ 16° Quel est le cas de base (et la condtion d'arrêt) de votre fonction ? Montrer son empilement et son dépilement pour l'appel produit(5,3)
✎ 17° Réaliser une fonction puissance() récursive correspondant à cette manière de voir la multiplication : 56 = 5*5*5*5*5*5.
Attention aux spécifications d'entrée : x et n sont des entiers, n étant positif.
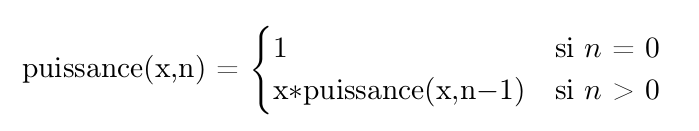
✎ 18° Quelle est la condition d'arrêt et le cas de base de votre fonction ? Montrer son empilement et son dépilement pour puissance(5,3)
✎ 19° Réaliser une fonction factorielle() récursive correspondant à la définition de la factorielle d'un entier : 5! = 5*4*3*2*1.
Attention aux spécifications d'entrée : n est un entier positif.
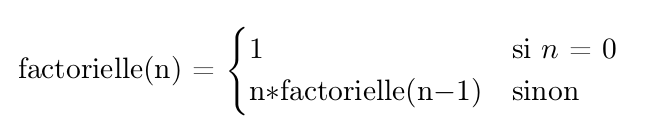
✎ 20° Quelle est la condition d'arrêt et le cas de base de votre fonction ? Montrer son empilement et son dépilement pour factorielle(5)
5 - Récursivité dans la nature
La nature regorge de structure de ce genre. Vous avez déjà regardé un brocolis de près ?
Voici un programme comportant une procédure permettant de tracer la courbe de Kock.
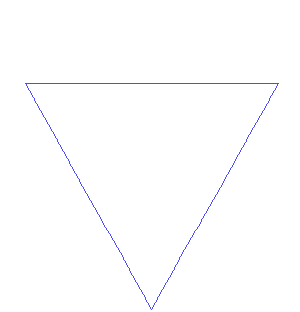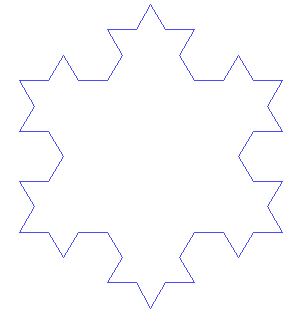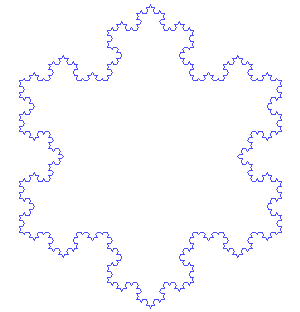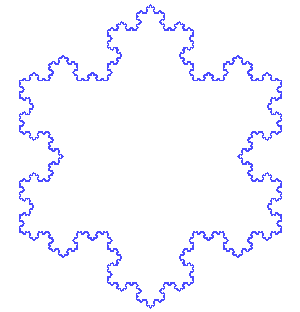
21° Tester le programme avec des valeurs plus petites de n valant 0, puis 1, puis 2... pour voir le principe.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18 | |
On voit ainsi que pour courber la courbe pour n = 2, on lance 3 versions de la courbe pour n=1 en tournant de façon intelligente entre chaque appel.
Pour créer un flocon de Kock, il suffit de faire appel à la même courbe de Kock en tournant de 120° entre chaque courbe.
22° Tester le programme avec des valeurs plus petites de n valant 0, puis 1, puis 2... pour voir le principe.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 | |
Pour en apprendre plus sur ce flocon, inventée en 1904 par le mathématicien suédois Helge von Koch, voici la page Wikipédia.
🏠 DM° Réaliser le Devoir Maison (voir le lien) en rédigeant correctement vos réponses.
DM à réaliser (05 questions)
6 - FAQ
En terme de place en mémoire, ça donne quoi ?
On dit souvent à propos de la récursivité qu'une fonction s'appelle elle-même. En réalité, c'est faux.
Il faut voir la déclaration d'une fonction comme la déclaration d'un mode d'emploi, d'une notice mais c'est tout.
Par contre, lorsqu'on lance un appel à une fonction, on crée une vraie fonction concrête avec son propre espace mémoire.
Ainsi, si vous lancez l'appel de f(5) et un autre appel à f(5), vous allez en réalité avoir deux espaces mémoires différents : chacune de ces deux fonctions aura son propre espace des noms et ses propres variables.
Pourquoi cette précision sur la place mémoire ?
Pour signaler que la récursivité n'est pas un moyen magique de trouver la solution d'un problème. Si, en moyenne, une fonction courbe() a besoin d'une place mémoire de 800 octets pour répondre, et qu'on a besoin de 1000 appels récursifs pour répondre au problème, au plus haut de l'empilement des fonctions, nous aurons donc besoin d'un espace mémoire de 1000*800 octets, soit 800 000 octets, soit 800 ko.
Chaque appel récursif constitue donc une fonction indépendante, ayant ses propres variables, son propre espace des noms ect... Et cet espace occupe la mémoire tant que cette version de la fonction n'a pas pu répondre car elle attend la réponse d'une autre version d'elle-même.
Activité publiée le 10 09 2020
Dernière modification : 07 09 2022
Auteur : ows. h.