2 - Graphes et relations sociales
Les réseaux sociaux stockent des informations sur vous et vos gouts, c'est un fait.
Mais comment parviennent-ils à savoir qui connait qui ?
Encoder un texte, ok : un octet représente un caractère. 65 pour A, 66 pour B...
Encoder une image, c'est plus compliqué. Nous avons vu qu'on utilise 3 valeurs RBG pour encoder la couleur du pixel. Il suffit de le faire pour chaque pixel.
Mais ... des relations sociales... Ca s'encode comment cette histoire ?
Documents de cours : open document ou pdf
Evaluation ✎ : questions 09-10-11-12
1 - Graphes
Il existe un objet mathématique bien pratique permettant de faire cela : le graphe.
Imaginons qu'on veuille représenter une communauté de 7 personnes identifiées par une lettre : A, B, C, D, E, F et G.
L'une des façons les plus intuitives de représenter leurs relations est la suivante :
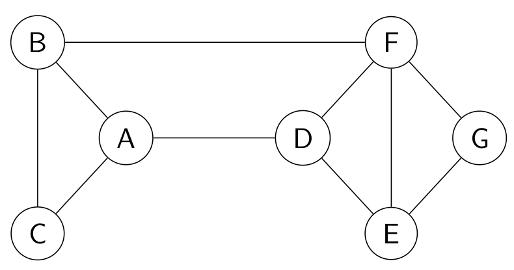
01° Sur ce graphe : Quels sont les gens qui connaissent A ? Quels sont les gens que connait A ?
...CORRECTION...
On voit qu'il y a un "lien" entre A et B, A et C et A et D.
On peut donc dire que A est connu de B, C et D.
On peut donc dire que A connait B, C et D.

02° Sur ce graphe : Quels sont les gens qui connaissent G ? Quels sont les gens que connait G ?
...CORRECTION...
On voit qu'il y a un "lien" entre G et F et G et E.
On peut donc dire que G est connu de E et F.
On peut donc dire que G connait E et F.

03° D'un point de vue purement comptable, A est-il plus populaire ou moins populaire que G
...CORRECTION...
A possède 3 relations.
G possède 2 relations.
A est donc plus populaire que G.

04° A combien de poignées de mains A et G se situent-ils ?
...CORRECTION...
A connait D. D connait E. E connait G.
Nous avons donc trois poignées de main.
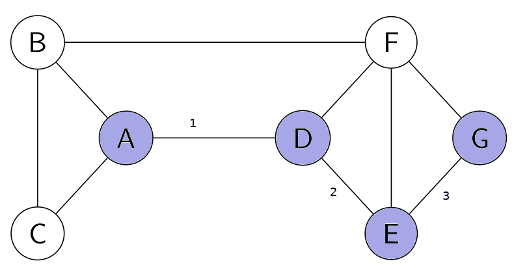
Graphes
Un graphe est un modèle abstrait constitué par :
- des sommets (aussi appelés nœuds ou points)
- Dans notre exemple : les personnes inscrites sur le réseau social
- des arêtes (ou liens) reliant ces sommets
- Dans notre exemple : les liens entre les personnes du réseau.
Que peut-on trouver comment informations sur graphe ?
- Deux sommets reliés par une arête sont dits adjacents : les personnes se connaissent.
- La longueur d'un chemin est le nombre d'arêtes successives à parcourir sur un chemin.
- La distance ente deux utilisateurs : la plus petite longueur entre deux utilisateurs. Attention, il peut y avoir plusieurs chemins mais on prend le plus court chemin.

05° Trouver la distance entre l'utilisateur A et les autres : A-B, A-C, A-D...
...CORRECTION...
Ceux à distance 0 : A (lui-même)
Ceux à distance 1 : B - C - D (les noeuds adjacents)
Ceux à distance 2 : E - F
Ceux à distance 3 : G
Graphes : caractérisation des sommets
Le degré d'un sommet est le nombre d'arêtes qui partent de ce sommet (ses liens).
L'excentricité d'un sommet est la distance la plus grande qu'on peut trouver à partir de ce sommet.

06° Trouver le degré et l'excentricité (la distance max entre ce sommet et le sommet le plus 'lointain') des différents sommets.
...CORRECTION...
A : degré 3 - excentricité 3 (voir la question précédédente).
B : degré 3 - excentricité 2.
Ceux à distance 1 : A - C - F (les noeuds adjacents)
Ceux à distance 2 : D - F - G
C : degré 2 - excentricité 3.
Ceux à distance 1 : A - B (les noeuds adjacents)
Ceux à distance 2 : D - F
Ceux à distance 3 : E - G
D : degré 3 - excentricité 2.
Ceux à distance 1 : A - E - F (les noeuds adjacents)
Ceux à distance 2 : B - C - G
E : degré 3 - excentricité 3.
Ceux à distance 1 : D - F - G (les noeuds adjacents)
Ceux à distance 2 : A - B
Ceux à distance 3 : C
F : degré 4 - excentricité 2.
Ceux à distance 1 : B - D - E - G (les noeuds adjacents)
Ceux à distance 2 : A- C
G : degré 2 - excentricité 3.
Ceux à distance 1 : E - F (les noeuds adjacents)
Ceux à distance 2 : B - D
Ceux à distance 3 : A - C
07° Vous désirez toucher un maximum de personnes sur le réseau social précédent. Par quel utilisateur passer ? (on parlera d'influenceur)
...CORRECTION...
F est le meilleur choix : meilleur degré et meilleur excentricité. Au moins, c'est simple.
Graphes : caractérisation des graphes
On peut caractériser un graphe par son nombre de sommets : plus ils sont nombreux, plus le parcourir devient complexe.
On nomme ordre d'un graphe son nombre de sommets.
On nomme diamètre D d'un graphe l'excentricité maximale trouvée parmi les sommets.
On nomme rayon R d'un graphe l'excentricité minimale trouvée parmi les sommets.
On nomme centre d'un graphe un sommet dont l'excentricité correspond au rayon.

08° Trouver l'ordre, le diamètre et le rayon de ce graphe. Quels sont les sommets qu'on peut qualifier de centre ?
A : degré 3 - excentricité 3 (c'est la distance AG).
B : degré 3 - excentricité 2.
C : degré 2 - excentricité 3.
D : degré 3 - excentricité 2.
E : degré 3 - excentricité 3.
F : degré 4 - excentricité 2.
G : degré 2 - excentricité 3.
...CORRECTION...
On a 7 sommets. On dit donc que c'est un graphe d'ordre 7.
L'excentricité maximale est de 3 : on peut écrire que le diamètre est D = 3
L'excentricité minimale est de 2 : on peut écrire que le rayon est R = 2
On peut donc dire que les sommets B, D et F sont des sommets de ce graphe.
Attention, contrairement au cercle, on ne peut pas dire que D = 2 R !
Derrière tout ceci se cache une théorie informatique et mathématique permettant de faire beaucoup de choses. Nous allons la retrouver avec Internet, avec le choix de trajets sur une carte... Beaucoup de problèmes à priori non traitable par les mathématiques deviennent d'une grande simplicité lorsqu'on utilise l'outil adapté : le graphe !
2 - phénomène du petit monde
En 1929, le Hongrois Frigyes Karinthy évoque la possibilité suivante : nous sommes reliés à toute autre personne sur Terre par six poignées de main au maximum.

Cela peut effectivement aller très vite : vous connaissez quelqu'un qui connait quelqu'un qui connait une femme politique de premier rang. Celle-ci connait donc d'autres personnes de ce même milieu et on repart dans l'autre sens.
L’expérience de Milgram ou expérience du petit monde est une expérience réalisée entre 1960 et 1963 par le psychologue américain Stanley Milgram. On la nomme aussi l'expérience du petit monde.

Il a demandé à 60 personnes de joindre un destinataire bien précis qu'on nommera A. Pour cela, ils devaient suivre une méthode assez précise.
Ils devaient écrire un courrier uniquement à quelqu'un qu'ils connaissaient réellement en leur demander de joindre la personne A. Le courrier devait indiquer systématiquement la liste des destinataires précédents.
On pouvait ainsi garantir le fait que les gens se connaissaient et garder la trace des communications.
Milgram publiera les résultats en déclarant qu'une lettre est parvenue au destinataire en quatre étapes seulement. Néanmoins, uniquement 5% des lettres parvinrent à destination au final. L'expérience n'en devint pas moins célèbre.
Avec les moyens modernes de communication, on peut beaucoup plus facilement faire des calculs sur les liaisons entre individus. Du moins, entre individus ayant accès à Internet !
Plusieurs études réalisées par Facebook ou Google montrent qu'on s'approche maintenant bien de 4 degrés de séparation entre n'importe qui sur Terre.
Attention, Milgram a également réalisé une expérience (portant le même nom du coup) liée au degré d'obéissance des individus.
3 - Exercices
Exercices Exercices09° Trouver l'ordre, le diamètre D et le rayon R de ce graphe. Trouver le ou les centres. Pour cela, il faudra chercher l'excentricité minimale et maximale.
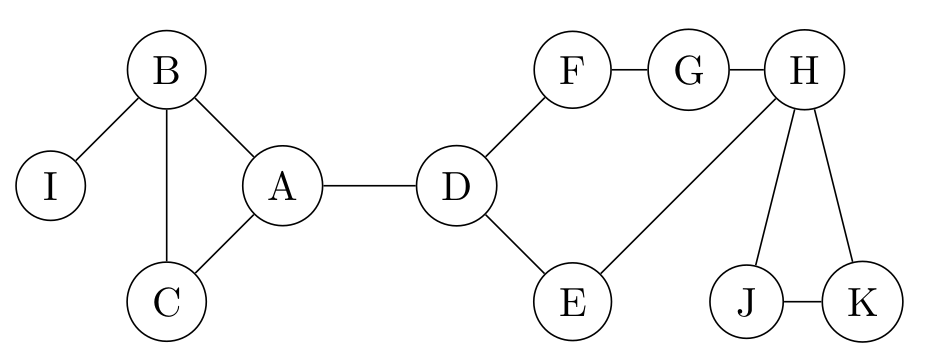
10° On parle parfois de ponts comme des connexions qui, si elles sont brisées, coupent les communications entre deux sous-graphes (on pourrait dire ici des communautés). Voyez-vous des ponts sur ces graphes ?

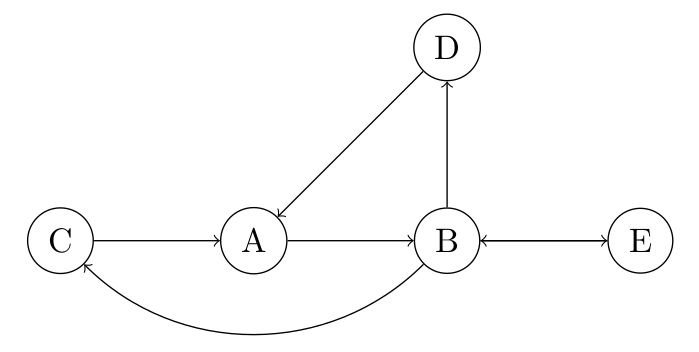
11° Tous les graphes que nous avons vu sont des graphes non orientés. Sont-ils capables de représenter les réseaux sur lesquels on peut suivre les publications de quelqu'un sans pour autant que cette personne ne vous suive ?
12° Quel sens pourriez-vous donner à ce graphe ?
Activité publiée le 11 03 2020
Dernière modification : 25 06 2022
Auteur : ows. h.