2 - Les pixels des images numériques
La photographie numérique (et sa gestion : stockage, modifications, améliorations) est devenue aujourd'hui l'un des principaux arguments de vente des smartphones. Nous allons tenter de voir comment on parvient à acquérir une image numérique de la réalité puis comment on parvient à la restituer à l'écran.
Documents de cours : open document ou pdf
1 - Pixels
Une image visible sur un écran d'ordinateur est juste la juxtapostion de petits carrés qu'on nomme des pixels.
Voici à titre d'exemple, voici le signe du langage Python et un agrandissement


Ou encore une image du Golden Gate :


Définir une image revient donc à définir la couleur qu'on veut voir s'afficher sur chacun des pixels.
Nous avons vu dans la partie Web qu'on définit cette couleur à l'aide uniquement de trois couleurs :
color : #FF8822;
- Le rouge, red en anglais, a ici l'intensité maximale FF
- le vert, green en anglais, a ici une intensité 88
- le bleu, blue en anglais, a ici une intensité 22
Pourtant, si on fait un zoom sur la partie jaune du Python, on peut voir cela
Une question se pose donc : comment parvenir à afficher du jaune à l'aide uniquement de rouge, de vert et de bleu ?
En réalité, chaque pixel est lui-même séparé en trois sous-pixels : un rectange ROUGE, un rectange VERT et un rectangle BLEU.
Voici un pixel vu de très très près. On a activé à fond les intensités RGB (red-green-blue) ou RVB (rouge-vert-bleu) :
En 4x4 pixels de plus loin
En 10x10 pixels de plus loin
En 30 x 30 pixels
Si on continue encore à réduire la taille affichée du pixel :
Voici donc comment on parvient à obtenir du blanc : lorsqu'on envoie du Rouge, du Vert et du Bleu à grande intensité, les 3 cônes de l'oeil sont activés et le cerveau interprète cela en BLANC.
Si on active uniquement le rouge et le vert, on obtient ceci :
En 4x4 pixels de plus loin
En 10x10 pixels de plus loin
En 30 x 30 pixels
Si on continue encore à réduire la taille affichée du pixel, on aura l'impression de voir du jaune :
Bilan :
Vous allez voir en sciences physiques qu'il existe deux synthèses de la lumière :
- la synthèse soustractive (on éclaire des objets qui ne brillent pas d'eux même dans le noir). C'est le cas d'un mélange de gouaches par exemple.
- la synthèse additive : un objet émet plusieurs radiations à la fois. C'est le cas ici : votre écran allumé brille bien de lui-même dans le noir.
Bien entendu, une synthèse ne peut avoir lieu que si l'oeil n'est pas en capacité de distinguer les différents pixels. Sur un écran moderne de smartphone, ils sont tellement petits que même avec une loupe vous n'avez que peu de chances de les voir !
Les 8 cas typiques de synthèse additive
Revoyons le principe des couleurs HTML fournies en code hexédacimal.
Code RGB couleur HTML en hexadécimal
On peut définir une couleur à partir des trois intensités Rouge - Vert - Bleu (RVB en français) ou Red - Green - Blue (RGB en anglais).
Exemple : color:#333333;.
#333333 veut dire qu'on a
- une intensité rouge de
33 33pour le vert- et
33pour le bleu.
Votre oeil reçoit un peu de rouge, un peu de vert et un peu de bleu, il interprète cela en gris foncé.
Les valeurs sont à fournir en hexadécimal (un système de numération où les chiffres vont de 0 à F...)
00 < 11 < 22 < 33 < 44 < 55 < 66 < 77 < 88 < 99 < AA < BB < CC < DD < EE < FF
01° Quel code HTML hexadécimal fournir pour obtenir du blanc ? du noir du gris foncé ? du gris clair ?
R :
V :
B :
Attention, les valeurs non valides sont transformées en FF.
02° Quel code HTML hexadécimal fournir pour obtenir du jaune ? du orange ? du rouge foncé ?
Concrètement, quelle est la taille des pixels sur un écran ?
Ca dépend de la qualité de l'écran. En gros, la taille (on dit le pas) d'un pixel varie de 0,31 mm à 0,21 mm.
Les sous-pixels sont donc 3 fois plus fins. Le principe est bien qu'un oeil humain ne puisse pas distinguer les sous-pixels en étant à une distance d'utilisation typique.
Vocabulaire : résolution d'un écran ou d'une image
La résolution correspond aux pixels qu'on peut trouver sur une largeur et sur une hauteur.
| Type de matériel | Définition typique |
|---|---|
| Moniteur classique - | de 800 pixels de large sur 600 pixels de large : 800 x 600 |
| Moniteur classique + | 2515 x 1886 |
| Smartphone moyen | 960 x 640 |
En cliquant sur les propriétés d'une image, on peut trouver sa résolution; souvent sous la forme pixels en largeur x pixels en hauteur.
03° Que vaut la définition de l'image ci-dessous ?
04° Que vaut la définition de l'image ci-dessous ?
2 - Capter une photo ?
Nous avons donc vu comment générer une image sur un écran à partir de 3 informations (RGB) par pixel.
Mais comment créer une photo numérique ?
Pour fabriquer une photo numérique, il faut des photosites, des capteurs qui transforment l'éclairement lumineux en un nombre compris entre
- 0 ou 00 (qui code une absence de luminosité) à
- 255 ou FF (qui code la luminosité maximale).

Si on ne fait que cela, on enregistre pas les couleurs, juste l'intensité : on aurait simplement une image en nuance de gris.
Pour obtenir une information sur les couleurs reçues, on place des filtres au dessus des photofiltres :
- Les filtres rouges laissent passer principalement les radiations rouges
- Les filtres verts laissent passer principalement les radiations rouges
- Les filtres bleus laissent passer principalement les radiations rouges
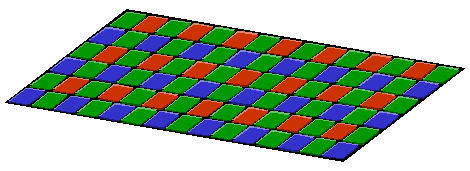
Quelques exemples avec deux envois de lumière blanche et un envoi de lumière jaune :

On voit que chaque photosite ne peut recevoir qu'une information : soit l'intensité 0-255 du rouge, soit l'intensité 0-255 du vert, soit l'intensité 0-255 du bleu.
05° Combien de photosites faut-il, dans le cas le plus simple, pour former un pixel
...CORRECTION...
Il en faut 4 puisqu'on a besoin d'une valeur pour le rouge, le vert et le bleu.
Par exemple, les informations pour créer l'un des pixels peuvent être récupérées à l'aide des 4 photosites et filtres suivants :
06° Pourquoi trouve-t-on deux fois plus de filtres verts ?
...CORRECTION...
Tout "simplement" car la lumière verte est plus facilement détectable par l'oeil humain. Le capteur de l'appareil photo se comporte ainsi plus comme un oeil humain en prenant deux fois plus de filtres verts que les deux autres.
Par information, nos yeux possèdent des cônes rouges, verts et bleus également.
07° On reçoit les intensités suivantes sur 4 photosites.
On a reçu 255 de rouge sur le photosite captant le rouge (en haut à gauche). Par contre, à cause du filtre rouge, nous ne savons pas combien de lumière verte ou de lumière bleue nous avons reçu au même endroit.
- Quelle valeur de rouge peut-on prendre pour les 4 photosites ?
- Quelle valeur de vert peut-on prendre pour les 4 photosites ?
- Quelle valeur de bleu peut-on prendre pour les 4 photosites ?
- En déduire la couleur qu'on stocker pour ces 4 photosites.
...CORRECTION...
Nous pourrions prendre R = 255 pour les 4 pixels.
Nous pourrions prendre G = (255+0)/2 = 127 pour les 4 pixels.
Nous pourrions prendre B = 10 pour les 4 pixels.
Pour chacun des 4 pixels, on peut ainsi décider de prendre RGB = (255, 125, 10)
Si les pixels sont suffisamment petits, nous allons percevoir une variation d'orange :
08° On reçoit les intensités suivantes sur 4 photosites.
- Quelle valeur de rouge peut-on prendre pour les 4 photosites ?
- Quelle valeur de vert peut-on prendre pour les 4 photosites ?
- Quelle valeur de bleu peut-on prendre pour les 4 photosites ?
- En déduire la couleur qu'on stocker pour ces 4 photosites.
...CORRECTION...
Nous pourrions prendre R = 170 pour les 4 pixels.
Nous pourrions prendre G = (170+170)/2 = 170 pour les 4 pixels.
Nous pourrions prendre B = 170 pour les 4 pixels.
Pour chacun des 4 pixels, on peut ainsi décider de prendre RGB = (170, 170, 170)
Si les pixels sont suffisamment petits, nous allons percevoir une variation de gris :
Si nous agissions juste ainsi, nous réduirions la qualité de l'image par 4 : 1 pixel possède la largeur et la hauteur de 2 photosites. Nous verrons comment faire mieux dans une autre activité.
3 - Pourquoi 255 ?
Une question subsiste : pourquoi mettre 255 comme valeur maximale ?
1er raison : ca suffit pour ne pas parvenir à distinguer deux cas successifs
Nous avons vu que l’intensité des trois couleurs de base (rouge, vert, bleu) est codée par un nombre compris entre 0 et 255. Pourquoi pas 0 et 358 ou 1 et 100 ?
Tout cela est lié à la façon de stocker les chiffres dans un ordinateur.
La plus petite unité mémoire est le bit : une case qui contient 0 ou 1. C’est l’un ou l’autre. Il s'agit donc de l'informatique la plus basique possible.
CODAGE DE L’INTENSITE SUR 1 bit :
Si on codait la couleur ROUGE sous cette forme, on aurait :
| Cas n° | Valeur binaire | Donne : | Visuel |
|---|---|---|---|
| Cas 0 | 0 | Pas de rouge | |
| Cas 1 | 1 | Rouge(100%) |
Avec 1 bit pour coder le rouge : on obtient donc 2 = 21 cas possibles : de 0 à 1.
CODAGE DE L’INTENSITE SUR 2 bits :
Si on codait la couleur ROUGE sous cette forme, on aurait :
| Cas n° | Valeur binaire | Donne : | Visuel |
|---|---|---|---|
| Cas 0 | 00 | Pas de rouge | |
| Cas 1 | 01 | Un peu(33%) | |
| Cas 2 | 10 | Beaucoup(66%) | |
| Cas 3 | 11 | Rouge(100%) |
Avec 2 bits pour coder le rouge : on obtient donc 4 = 2 * 2 = 22 cas possibles : de 0 à 3.
On voit bien qu'on obtient plus de nuances.
CODAGE DE L’INTENSITE SUR 3 bits :
Si on codait la couleur ROUGE sous cette forme, on aurait :
| Cas n° | Valeur binaire | Donne : | Visuel |
|---|---|---|---|
| Cas 0 | 000 | Pas de rouge | |
| Cas 1 | 001 | 14% | |
| Cas 2 | 010 | 29% | |
| Cas 3 | 011 | 43% | |
| Cas 4 | 100 | 57% | |
| Cas 5 | 101 | 71% | |
| Cas 6 | 110 | 86% | |
| Cas 7 | 111 | 100% |
Avec 3 bits pour coder le rouge : on obtient donc 8 = 2 * 2 * 2 = 23 cas possibles : de 0 à 7.
Bref, ensuite un peu plus de nuances.
09° Si on généralise, combien a-t-on de cas possibles avec 8 bits ? Sur combien de bits est codé l’intensité d’une couleur sachant que sa valeur varie de 0 à 255 ?
...CORRECTION...
Il y a 8 bits.
On calcule donc 28 et on trouve 256.
On compte jusqu'à 255 car on commence à 0, pas à 1 !
Pour vous donner une idée du nombre de nuances que cela représente, voilà les nuances de rouge pour 8 bits :
| Valeur | Visuel | Valeur | Visuel | Valeur | Visuel |
|---|---|---|---|---|---|
| 0 | 85 | 170 | |||
| 1 | 86 | 171 | |||
| 2 | 87 | 172 | |||
| 3 | 88 | 173 | |||
| 4 | 89 | 174 | |||
| 5 | 90 | 175 | |||
| 6 | 91 | 176 | |||
| 7 | 92 | 177 | |||
| 8 | 93 | 178 | |||
| 9 | 94 | 179 | |||
| 10 | 95 | 180 | |||
| 11 | 96 | 181 | |||
| 12 | 97 | 182 | |||
| 13 | 98 | 183 | |||
| 14 | 99 | 184 | |||
| 15 | 100 | 185 | |||
| 16 | 101 | 186 | |||
| 17 | 102 | 187 | |||
| 18 | 103 | 188 | |||
| 19 | 104 | 189 | |||
| 20 | 105 | 190 | |||
| 21 | 106 | 191 | |||
| 22 | 107 | 192 | |||
| 23 | 108 | 193 | |||
| 24 | 109 | 194 | |||
| 25 | 110 | 195 | |||
| 26 | 111 | 196 | |||
| 27 | 112 | 197 | |||
| 28 | 113 | 198 | |||
| 29 | 114 | 199 | |||
| 30 | 115 | 200 | |||
| 31 | 116 | 201 | |||
| 32 | 117 | 202 | |||
| 33 | 118 | 203 | |||
| 34 | 119 | 204 | |||
| 35 | 120 | 205 | |||
| 36 | 121 | 206 | |||
| 37 | 122 | 207 | |||
| 38 | 123 | 208 | |||
| 39 | 124 | 209 | |||
| 40 | 125 | 210 | |||
| 41 | 126 | 211 | |||
| 42 | 127 | 212 | |||
| 43 | 128 | 213 | |||
| 44 | 129 | 214 | |||
| 45 | 130 | 215 | |||
| 46 | 131 | 216 | |||
| 47 | 132 | 217 | |||
| 48 | 133 | 218 | |||
| 49 | 134 | 219 | |||
| 50 | 135 | 220 | |||
| 51 | 136 | 221 | |||
| 52 | 137 | 222 | |||
| 53 | 138 | 223 | |||
| 54 | 139 | 224 | |||
| 55 | 140 | 225 | |||
| 56 | 141 | 226 | |||
| 57 | 142 | 227 | |||
| 58 | 143 | 228 | |||
| 59 | 144 | 229 | |||
| 60 | 145 | 230 | |||
| 61 | 146 | 231 | |||
| 62 | 147 | 232 | |||
| 63 | 148 | 233 | |||
| 64 | 149 | 234 | |||
| 65 | 150 | 235 | |||
| 66 | 151 | 236 | |||
| 67 | 152 | 237 | |||
| 68 | 153 | 238 | |||
| 69 | 154 | 239 | |||
| 70 | 155 | 240 | |||
| 71 | 156 | 241 | |||
| 72 | 157 | 242 | |||
| 73 | 158 | 243 | |||
| 74 | 159 | 244 | |||
| 75 | 160 | 245 | |||
| 76 | 161 | 246 | |||
| 77 | 162 | 247 | |||
| 78 | 163 | 248 | |||
| 79 | 164 | 249 | |||
| 80 | 165 | 250 | |||
| 81 | 166 | 251 | |||
| 82 | 167 | 252 | |||
| 83 | 168 | 253 | |||
| 84 | 169 | 254 | |||
| 85 | 170 | 255 |
255 représente donc sur 8 bits l'intensité maximale de rouge.
Mais comment faire le lien entre 255 et les 8 bits ?
Pour transformer un nombre binaire en nombre en base 10 (notre base naturelle puisqu’on a 10 doigts), il faut savoir que :
- Le bit le plus à droite est nommé le bit de poids faible car il code uniquement 1.
- Le bit juste d’à côté code 2.
- Celui d’encore après code 4
- ...
Voilà un exemple pour un nombre binaire de 8 bits (on appelle cela un octet), M = 1010 1011.
| Nombre M = | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| Les bits codent | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| On obtient donc | 128 | 32 | 8 | 2 | 1 |
D'ou la valeur de M en base 10 :
M = 128 + 32 +8 + 2 + 1 = 171.
10° Trouver l'octet le plus grand en activant tous les bits à 1 : 1111 1111.
...CORRECTION...
On calcule 128+64+32+16+8+4+2+1 et ça donne 255.
Pour finir : un exemple de convertisseur automatique d'OCTET pour la forme :
Votre nombre binaire M :
| Nombre M = | ||||||||
| Les bits codent | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| On obtient donc |
D'ou la valeur de M en base 10 : M = = .
Activité publiée le 06 11 2019
Dernière modification : 06 11 2019
Auteur : ows. h.