13 - Implementation Python de knn
Nous allons voir aujourd'hui comment implémenter l'algorithme des k plus proches voisins (k nearest neighbors) en Python.
Logiciel nécessaire pour l'activité : Python 3 : Thonny, IDLE ou le site repl.it ...
Prérequis : Python : k plus proches voisins
Evaluation ✎ : questions 04-10-11-12-14-17
Documents de cours :
1 - Rappel rapide sur le knn
Le principe global des knn est de calculer les distances entre les différents enregistrements et un enregistrement dont on ne connaît pas la catégorie.
On attribue alors à l'enregistrement inconnu la catégorie la plus courante parmi les k plus proches voisins.
Nous avions décomposé l'algorithme en 4 parties (et réalisé les deux premières avec Python) :
- Etape 1 : calculs et stockage des distances sur k enregistrements
- Stocker les distances de k premiers enregistrements dans un tableau memoire
- Trier les k enregistrements dans memoire en fonction de la distance
- Etape 2 : calcul des distances sur les autres enregistrements et stockage au cas par cas
- Pour chaque enregistrement restant :
- calculer la distance
- si cette distance est plus petite que la plus grande des distances mémorisées : remplacer la plus grande par la nouvelle et trier à nouveau le tableau memoire
- Etape 3 : analyse des catégories dans les k plus proches voisins
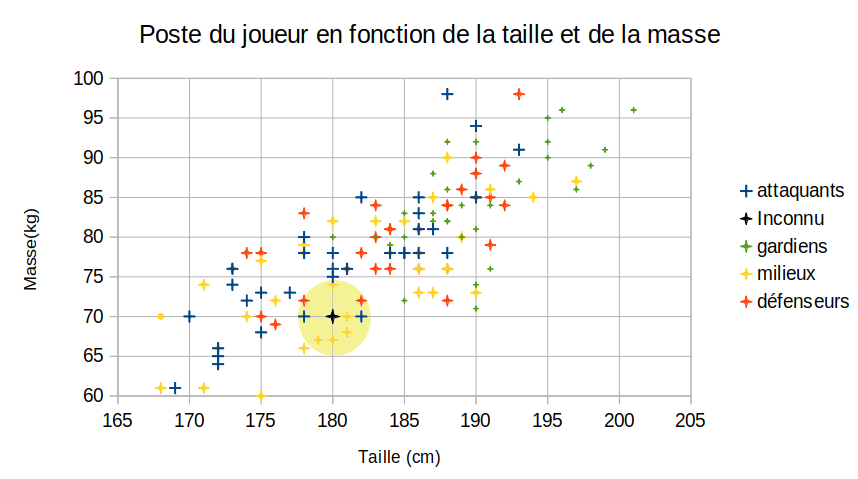
- On compte les catégories présentes dans le tableau memoire (ici, il s'agit des 9 enregistrements présents dans le cercle jaune)
- Etape 4 : conception de la réponse à renvoyer
- On renvoie la catégorie la plus présente (ici les violets, soit les milieux de terrain)
⚐ Etape 1 ➡ ajout de k couples (distance, catégorie) dans memoire
memoire ← Tableau vide ayant longueur éléments
index ← 0
TANT QUE index < k
d ← distance (nouveau, collection[index])
on calcule la distance entre les deux enregistrements
categorie ← collection[index]['Poste']
on récupère la catégorie de l'enregistrement via la clé 'Poste'
memoire[index] ← (d, categorie)
on mémorise un couple (p-uplet) contenant distance et catégorie
index ← index + 1
on avance dans la lecture de la collection
Fin du TANT QUE
trie(memoire) en ordre croissant de distance (l'index 0)
laPlusGrande ← memoire[k-1][0]
⚐ Etape 2 ➡ on lit la suite mais on ne mémorise que si la distance est plus petite que l'une des précédentes
TANT QUE index < longueur de la collection
d ← distance (nouveau, collection[index])
On calcule la distance entre les deux enregistrements
SI d < laPlusGrande en mémoire
categorie ← collection[index]['Poste']
On récupère la catégorie de l'enregistrement
memoire[k-1] ← (d, categorie)
On place le couple (distance,catégorie) en mémoire en dernière position
trie(memoire) en ordre croissant de distance (l'index 0)
laPlusGrande ← memoire[k-1][0]
Fin du SI
index ← index + 1
Fin du TANT QUE
⚐ Etape 3 ➡ on compte les catégories présentes
nombres ← Dictionnaire vide
index ← 0
TANT QUE index < k
categorie ← memoire[index][1]
SI la clé categorie existe déjà dans le dictionnaire nombres
nombres[categorie] ← nombres[categorie] + 1
SINON
nombres[categorie] ← 1
Fin du SI
Fin TANT QUE
⚐ Etape 4 : on renvoie la catégorie majoritaire
reponse ← cleMajoritaire(nombres)
Renvoyer reponse
2 - Téléchargement des ressources
J'estime que vous savez désormais gérer vos dossiers et vos téléchargements. Nous allons donc juste télécharger les ressources à l'aide d'un programme Python. Ca ira plus vite que de tout faire à la main.
01° Créer un dossier nommé knn2 sur votre poste. Créer un fichier Python nommé recuperation.py contenant ce code
1
2
3
4
5 | import urllib.request
urllib.request.urlretrieve('https://doc.infoforall.fr/activite/algo/cours/knn/creation_collection.py', 'creation_collection.py')
urllib.request.urlretrieve('https://doc.infoforall.fr/activite/algo/cours/knn/entrainement.csv', 'entrainement.csv')
urllib.request.urlretrieve('https://doc.infoforall.fr/activite/algo/cours/knn/test.csv', 'test.csv')
urllib.request.urlretrieve('https://doc.infoforall.fr/activite/algo/cours/knn/gestion_initiale_2.py', 'gestion.py')
|
La fonction urlretrieve du module request contenu dans urllib permet de créer un téléchargement en fournissant l'URL voulue et le nom sous lequel on veut enregistrer le téléchargement.
Lancer le code. Vous devriez obtenir un dossier contenant les 5 fichiers suivants :
Si ce n'est pas le cas, il est temps de créer cette structure et de télécharger les fichiers (clic-droit, télécharger sous).
Certains sites connus bloquent le hotlinking : le fait de télécharger une ressource (images, vidéos...) sans que la demande ne soit effectuée via une page HTML du site lui-même.
Pourquoi ? Pour éviter par exemple qu'un site n'utilise votre serveur pour afficher des images sur son site. Sur un petit site, ça ne pose pas de problème habituellement. Par contre, sur un site apparaissant régulièrement dans les premières pages des recherches d'images, cela peut mener à un pourcentage non négligeable de téléchargements d'images pour des pages externes.
Voici le contenu du programme gestion.py (inutile de le lire, nous allons l'analyser et le compléter lors des questions suivantes).
Il contient :
- La fonction distance qui estime la distance entre deux enregistrements contenant au moins la masse et la taille du joueur.
- La fonction knn qui réalise une partie de l'étape 1. On doit lui fournir les paramètres suivants : k, l'enregistrement nouveau à analyser et la collection des enregistrements connus.
02° Lancer le programme gestion.py.
Taper les instructions suivantes pour vérifier qu'il répond bien :
>>> joueurs[0]
{'Poste': 'Attaquant', 'Taille (cm)': 178, 'Masse (kg)': 80}
Cela permet de vérifier que les enregistrements contenus dans notre collection-tableau joueurs sont des dictionnaires.
>>> knn(3, enr_test, joueurs)
[
(6.4031242374328485, 'Attaquant'),
(3.605551275463989, 'Attaquant'),
(23.769728648009426, 'Attaquant')
]
La fonction knn renvoie donc une collection de tuples. Ces tuples contiennent la distance et la catégorie des k premiers enregistrements dans la collection. Ce ne sont pas nécessairement les plus proches.
Comme les premiers enregistrements du fichiers CSV sont les attaquants, la catégorie est toujours la même...
3 - Réaliser l'étape 1 avec Python
Nous allons pouvoir analyser l'étape 1 : mémoriser les k premiers distances et catégories de joueurs dans notre collection.
Rappel
Etape 1
⚐ Etape 1 ➡ ajout de k couples (distance, catégorie) dans memoire
memoire ← Tableau vide ayant longueur éléments
index ← 0
TANT QUE index < k
d ← distance (nouveau, collection[index])
on calcule la distance entre les deux enregistrements
categorie ← collection[index]['Poste']
on récupère la catégorie de l'enregistrement via la clé 'Poste'
memoire[index] ← (d, categorie)
on mémorise un couple (p-uplet) contenant distance et catégorie
index ← index + 1
on avance dans la lecture de la collection
Fin du TANT QUE
trie(memoire) en ordre croissant de distance (l'index 0)
laPlusGrande ← memoire[k-1][0]
Pour cela, nous allons créer une fonction knn qui possède trois paramètres.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54 | # 1 - Importation
from creation_collection import creer_collection
from matplotlib import pyplot as plt
from math import sqrt
from operator import itemgetter
# 2 - Déclaration des fonctions
def distance(enr1, enr2):
"""Fonction qui renvoie la distance entre les deux enregistrements
:: param enr1 (dict) :: un dictionnaire correspondant à un enregistrement
:: param enr2 (dict) :: un dictionnaire correspondant à un enregistrement
:: return (float) :: la distance euclidienne entre les deux enregistrements
"""
x1 = enr1['Taille (cm)']
x2 = enr2['Taille (cm)']
y1 = enr1['Masse (kg)']
y2 = enr2['Masse (kg)']
d = sqrt( (x2-x1)**2 + (y2-y1)**2 )
return d
def knn(k, nouveau, collection):
"""Fonction qui renvoie la catégorie supposée de nouveau
:: param k(int) :: le nombre de plus proches voisins à gérer
:: param nouveau(dict) :: un enregistrement sans connaissance de la clé de catégorie
:: param collection(list) :: une collection d'enregistrements
:: return (list) :: un tableau contenant la ou les catégories majoritaires
"""
memoire = []
for index in range(k):
d = distance(nouveau, collection[index])
categorie = collection[index]['Poste']
memoire.append( (d,categorie) )
return memoire
# 3 - Programme
if __name__ == '__main__':
# Collection : Création de la collection
joueurs = creer_collection("entrainement.csv")
# Collection : transformation en entiers des descripteurs numériques
for index in range(len(joueurs)):
joueurs[index]['Taille (cm)'] = int(joueurs[index]['Taille (cm)'])
joueurs[index]['Masse (kg)'] = int(joueurs[index]['Masse (kg)'])
enr_test = {'Poste':'X', 'Taille (cm)':182, 'Masse (kg)':75}
|
03° Lancer le programme gestion.py.
Lancer les instructions suivantes dans la console de façon à calculer la distance entre notre enregistrement de catégorie inconnue enr_test et les k enregistrements de la collection.
>>> knn(1, enr_test, joueurs)
[ (6.4031242374328485, 'Attaquant') ] <--enregistrement 0
>>> knn(3, enr_test, joueurs)
[ (6.4031242374328485, 'Attaquant'), <--enregistrement 0
(3.605551275463989, 'Attaquant'), <--enregistrement 1
(23.769728648009426, 'Attaquant') ] <--enregistrement 2
>>> knn(5, enr_test, joueurs)
[ (6.4031242374328485, 'Attaquant'),
(3.605551275463989, 'Attaquant'),
(23.769728648009426, 'Attaquant'),
(3.605551275463989, 'Attaquant'),
(19.1049731745428, 'Attaquant') ]
On remarque au passage que les joueurs des enregistrements 1 et 3 ont manifestement le même profil poids - taille puisqu'ils ont exactement la même distance avec notre enregistrement inconnu.
Attention, il ne s'agit pas encore des k plus proches voisins : ce ne sont que les k premières distances dans la collection.
✎ 04° Expliquer rapidement en français ce que fait cette fonction ligne par ligne :
- ligne 35 : on ...
- ligne 36 : on ...
- ligne 37 : on ...
- ect ...
25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40def knn(k, nouveau, collection): """Fonction qui renvoie la catégorie supposée de nouveau :: param k(int) :: le nombre de plus proches voisins à gérer :: param nouveau(dict) :: un enregistrement sans connaissance de la clé de catégorie :: param collection(list) :: une collection d'enregistrements :: return (list) :: un tableau contenant la ou les catégories majoritaires """ memoire = [] for index in range(k): d = distance(nouveau, collection[index]) categorie = collection[index]['Poste'] memoire.append( (d,categorie) ) return memoire
Il nous reste à trier le tableau memoire en fonction des valeurs croissantes des distances, à savoir l'index 0 des tuples contenus dans memoire.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18 | def knn(k, nouveau, collection):
"""Fonction qui renvoie la catégorie supposée de nouveau
:: param k(int) :: le nombre de plus proches voisins à gérer
:: param nouveau(dict) :: un enregistrement sans connaissance de la clé de catégorie
:: param collection(list) :: une collection d'enregistrements
:: return (list) :: un tableau contenant la ou les catégories majoritaires
"""
memoire = []
for index in range(k):
d = distance(nouveau, collection[index])
categorie = collection[index]['Poste']
memoire.append( (d,categorie) )
memoire.sort(key=itemgetter(0))
laPlusGrande = memoire[k-1][0]
return memoire
|
Ce dernier tri, visible en ligne 16 ici n'est pas facile à faire : il faut trier les couples (distance, catégorie) en les replaçant du couple qui a la plus petite distance au couple qui a la plus grande distance.
Exemple :
>>> knn(5, enr_test, joueurs)
[
(6.4031242374328485, 'Attaquant'),
(3.605551275463989, 'Attaquant'),
(23.769728648009426, 'Attaquant'),
(3.605551275463989, 'Attaquant'),
(19.1049731745428, 'Attaquant')
]
On veut que cela devienne cela :
>>> knn(5, enr_test, joueurs)
[
(3.605551275463989, 'Attaquant'),
(3.605551275463989, 'Attaquant'),
(6.4031242374328485, 'Attaquant'),
(19.1049731745428, 'Attaquant'),
(23.769728648009426, 'Attaquant'),
]
Pour cela, on utilise la méthode sort en lui fournissant une fonction-opérateur (importée en ligne 6 attention) nommée itemgetter. Il s'agit juste d'un outil bien pratique pour gérer les tables avec Python :
16 |
memoire.sort(key=itemgetter(0))
|
Cela veut dire : prend le tableau memoire et trie avec la méthode sort les enregistrements du tableau en fonction de la colonne 0 des enregistrements.
On notera que cette méthode sort avec une clé itemgetter fonctionne que les enregistrements soient des tableaux ou des tuples. Le tout est qu'on puisse identifier la colonne à surveiller à l'aide d'un index.
05° Pourquoi trier cette collection-tableau par rapport à l'index 0 des enregistrements-tuples qu'elle contient (en d'autres termes, quelle est l'information contenue dans cet index 0) ?
Remplacer ensuite la fonction knn par la nouvelle fonction fournie. Lancer les nouvelles instructions pour voir que le tableau-collection renvoyé par la fonction est bien trié maintenant.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18 | def knn(k, nouveau, collection):
"""Fonction qui renvoie la catégorie supposée de nouveau
:: param k(int) :: le nombre de plus proches voisins à gérer
:: param nouveau(dict) :: un enregistrement sans connaissance de la clé de catégorie
:: param collection(list) :: une collection d'enregistrements
:: return (list) :: un tableau contenant la ou les catégories majoritaires
"""
memoire = []
for index in range(k):
d = distance(nouveau, collection[index])
categorie = collection[index]['Poste']
memoire.append( (d,categorie) )
memoire.sort(key=itemgetter(0))
laPlusGrande = memoire[k-1][0]
return memoire
|
Avant la modification :
>>> knn(5, enr_test, joueurs)
[
(6.4031242374328485, 'Attaquant'),
(3.605551275463989, 'Attaquant'),
(23.769728648009426, 'Attaquant'),
(3.605551275463989, 'Attaquant'),
(19.1049731745428, 'Attaquant')
]
Maintenant (normalement) :
>>> knn(5, enr_test, joueurs)
[
(3.605551275463989, 'Attaquant'),
(3.605551275463989, 'Attaquant'),
(6.4031242374328485, 'Attaquant'),
(19.1049731745428, 'Attaquant'),
(23.769728648009426, 'Attaquant')
]
...CORRECTION...
Tout simplement car on veut trier par rapport aux distances calculées et que ces distances sont placées dans la colonne 0.
Et enfin, la dernière mini-étape : on mémorise la plus grande distance parmi les k mémorisées pour l'instant :
17 |
laPlusGrande = memoire[k-1][0]
|
On prend la position k-1 car il y a k éléments mais les index vont de 0 à k-1.
Nous allons maintenant pouvoir passer à l'étape 2 et ça va être rapide.
4 - Réaliser l'étape 2 avec Python
L'étape 2 consiste à maintenant regarder si la distance de l'enregistrement suivant est plus petite que celles enregistrées dans memoire.
Dans ce cas, on remplace la plus grande des anciennes distances mesurées par celle-ci.
Rappel
Rappel Etape 2
⚐ Etape 2 ➡ on lit la suite mais on ne mémorise que si la distance est plus petite que l'une des précédentes
TANT QUE index < longueur de la collection
d ← distance (nouveau, collection[index])
On calcule la distance entre les deux enregistrements
SI d < laPlusGrande en mémoire
categorie ← collection[index]['Poste']
On récupère la catégorie de l'enregistrement
memoire[k-1] ← (d, categorie)
On place le couple (distance,catégorie) en mémoire en dernière position
trie(memoire) en ordre croissant de distance (l'index 0)
laPlusGrande ← memoire[k-1][0]
Fin du SI
index ← index + 1
Fin du TANT QUE
06° Corriger le code de l'étape 2 dans la fonction knn fournie ci-dessous pour qu'elle soit fonctionnelle. Pour l'instant, il y a une erreur quelque part entre la ligne 44 et 51.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67 | # 1 - Importation
from creation_collection import creer_collection
from matplotlib import pyplot as plt
from math import sqrt
from operator import itemgetter
# 2 - Déclaration des fonctions
def distance(enr1, enr2):
"""Fonction qui renvoie la distance entre les deux enregistrements
:: param enr1 (dict) :: un dictionnaire correspondant à un enregistrement
:: param enr2 (dict) :: un dictionnaire correspondant à un enregistrement
:: return (float) :: la distance euclidienne entre les deux enregistrements
"""
x1 = enr1['Taille (cm)']
x2 = enr2['Taille (cm)']
y1 = enr1['Masse (kg)']
y2 = enr2['Masse (kg)']
d = sqrt( (x2-x1)**2 + (y2-y1)**2 )
return d
def knn(k, nouveau, collection):
"""Fonction qui renvoie la catégorie supposée de nouveau
:: param k(int) :: le nombre de plus proches voisins à gérer
:: param nouveau(dict) :: un enregistrement sans connaissance de la clé de catégorie
:: param collection(list) :: une collection d'enregistrements
:: return (list) :: un tableau contenant la ou les catégories majoritaires
"""
# Etape 1 - ajout de k couples (distance, catégorie) dans memoire
memoire = []
for index in range(k):
d = distance(nouveau, collection[index])
categorie = collection[index]['Poste']
memoire.append( (d, categorie) )
memoire.sort(key=itemgetter(0))
laPlusGrande = memoire[k-1][0]
# Etape 2 - on rajoute les autres au cas par cas
for index in range(k, len(collection)):
d = distance(nouveau, collection[index])
if d > laPlusGrande:
categorie = collection[index]['Poste']
memoire[k-1] = (d, categorie)
memoire.sort(key=itemgetter(0))
laPlusGrande = memoire[k-1][0]
return memoire
# 3 - Programme
if __name__ == '__main__':
# Collection : Création de la collection
joueurs = creer_collection("entrainement.csv")
# Collection : transformation en entiers des descripteurs numériques
for index in range(len(joueurs)):
joueurs[index]['Taille (cm)'] = int(joueurs[index]['Taille (cm)'])
joueurs[index]['Masse (kg)'] = int(joueurs[index]['Masse (kg)'])
enr_test = {'Poste':'X', 'Taille (cm)':182, 'Masse (kg)':75}
|
...CORRECTION...
L'erreur vient d'un signe < qui est devenu > lors de la frappe.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67 | # 1 - Importation
from creation_collection import creer_collection
from matplotlib import pyplot as plt
from math import sqrt
from operator import itemgetter
# 2 - Déclaration des fonctions
def distance(enr1, enr2):
"""Fonction qui renvoie la distance entre les deux enregistrements
:: param enr1 (dict) :: un dictionnaire correspondant à un enregistrement
:: param enr2 (dict) :: un dictionnaire correspondant à un enregistrement
:: return (float) :: la distance euclidienne entre les deux enregistrements
"""
x1 = enr1['Taille (cm)']
x2 = enr2['Taille (cm)']
y1 = enr1['Masse (kg)']
y2 = enr2['Masse (kg)']
d = sqrt( (x2-x1)**2 + (y2-y1)**2 )
return d
def knn(k, nouveau, collection):
"""Fonction qui renvoie la catégorie supposée de nouveau
:: param k(int) :: le nombre de plus proches voisins à gérer
:: param nouveau(dict) :: un enregistrement sans connaissance de la clé de catégorie
:: param collection(list) :: une collection d'enregistrements
:: return (list) :: un tableau contenant la ou les catégories majoritaires
"""
# Etape 1 - ajout de k couples (distance, catégorie) dans memoire
memoire = []
for index in range(k):
d = distance(nouveau, collection[index])
categorie = collection[index]['Poste']
memoire.append( (d, categorie) )
memoire.sort(key=itemgetter(0))
laPlusGrande = memoire[k-1][0]
# Etape 2 - on rajoute les autres au cas par cas
for index in range(k, len(collection)):
d = distance(nouveau, collection[index])
if d < laPlusGrande:
categorie = collection[index]['Poste']
memoire[k-1] = (d, categorie)
memoire.sort(key=itemgetter(0))
laPlusGrande = memoire[k-1][0]
return memoire
# 3 - Programme
if __name__ == '__main__':
# Collection : Création de la collection
joueurs = creer_collection("entrainement.csv")
# Collection : transformation en entiers des descripteurs numériques
for index in range(len(joueurs)):
joueurs[index]['Taille (cm)'] = int(joueurs[index]['Taille (cm)'])
joueurs[index]['Masse (kg)'] = int(joueurs[index]['Masse (kg)'])
enr_test = {'Poste':'X', 'Taille (cm)':182, 'Masse (kg)':75}
|
Pour information, nous avions déjà rencontré des ranges avec plusieurs nombres.
range
Taper range(6) permet d'obtenir l'ensemble suivant (0,1,2,3,4,5).
En réalité, Python remplit la valeur initiale par 0 et l'incrémentation par 1.
Taper range(6) revient à avoir tapé range(0, 6, 1)
Quelques exemples :
>>> for x in range(0,6,1) : print(x,end='-')
0-1-2-3-4-5-
>>> for x in range(2,6,1) : print(x,end='-')
2-3-4-5-
>>> for x in range(1,6,2) : print(x,end='-')
1-3-5-
>>> for x in range(6,1,-1) : print(x,end='-')
6-5-4-3-2-
Du coup, la ligne 45 veut dire de travailler sur des index compris dans l'intervalle [k ; nombre de joueurs - 1 ].
45 |
for index in range(k, len(collection)):
|
C'est fini. Il nous reste à voir les résultats que nous renvoie notre fonction (pas tout à fait finalisée mais fonctionnelle).
07° Relancer le nouveau programme avec la bonne fonction knn.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67 | # 1 - Importation
from creation_collection import creer_collection
from matplotlib import pyplot as plt
from math import sqrt
from operator import itemgetter
# 2 - Déclaration des fonctions
def distance(enr1, enr2):
"""Fonction qui renvoie la distance entre les deux enregistrements
:: param enr1 (dict) :: un dictionnaire correspondant à un enregistrement
:: param enr2 (dict) :: un dictionnaire correspondant à un enregistrement
:: return (float) :: la distance euclidienne entre les deux enregistrements
"""
x1 = enr1['Taille (cm)']
x2 = enr2['Taille (cm)']
y1 = enr1['Masse (kg)']
y2 = enr2['Masse (kg)']
d = sqrt( (x2-x1)**2 + (y2-y1)**2 )
return d
def knn(k, nouveau, collection):
"""Fonction qui renvoie la catégorie supposée de nouveau
:: param k(int) :: le nombre de plus proches voisins à gérer
:: param nouveau(dict) :: un enregistrement sans connaissance de la clé de catégorie
:: param collection(list) :: une collection d'enregistrements
:: return (list) :: un tableau contenant la ou les catégories majoritaires
"""
# Etape 1 - ajout de k couples (distance, catégorie) dans memoire
memoire = []
for index in range(k):
d = distance(nouveau, collection[index])
categorie = collection[index]['Poste']
memoire.append( (d,categorie) )
memoire.sort(key=itemgetter(0))
laPlusGrande = memoire[k-1][0]
# Etape 2 - on rajoute les autres au cas par cas
for index in range(k, len(collection)):
d = distance(nouveau, collection[index])
if d < laPlusGrande:
categorie = collection[index]['Poste']
memoire[k-1] = (d,categorie)
memoire.sort(key=itemgetter(0))
laPlusGrande = memoire[k-1][0]
return memoire
# 3 - Programme
if __name__ == '__main__':
# Collection : Création de la collection
joueurs = creer_collection("entrainement.csv")
# Collection : transformation en entiers des descripteurs numériques
for index in range(len(joueurs)):
joueurs[index]['Taille (cm)'] = int(joueurs[index]['Taille (cm)'])
joueurs[index]['Masse (kg)'] = int(joueurs[index]['Masse (kg)'])
enr_test = {'Poste':'X', 'Taille (cm)':182, 'Masse (kg)':75}
|
08° Utiliser l'instruction suivante avec k = 1. Fournir la réponse . Interpréter la réponse que devrait donner l'algorithme sur le type de catégorie(s) de joueur.
>>> knn(1, enr_test, joueurs)
...CORRECTION...
>>> knn(1, enr_test, joueurs)
[
(1.4142135623730951, 'Défenseur')
]
On va dire que c'est un profil de défenseur ?
09° Utiliser l'instruction suivante avec k = 3. Fournir la réponse . Interpréter la réponse que devrait donner l'algorithme sur le type de catégorie(s) de joueur.
>>> knn(3, enr_test, joueurs)
...CORRECTION...
>>> knn(3, enr_test, joueurs)
[
(1.4142135623730951, 'Défenseur'),
(2.0, 'Attaquant'),
(2.23606797749979, 'Défenseur')
]
On va dire que c'est un profil de défenseur car on a deux réponses défenseurs contre une réponse Attaquant.
✎ 10° Utiliser l'instruction suivante avec k = 5. Fournir la réponse . Interpréter la réponse que devrait donner l'algorithme sur le type de catégorie(s) de joueur.
>>> knn(5, enr_test, joueurs)
✎ 11° Utiliser l'instruction suivante avec k = 7. Fournir la réponse . Interpréter la réponse que devrait donner l'algorithme sur le type de catégorie(s) de joueur.
>>> knn(7, enr_test, joueurs)
5 - Etape 3 en Python
Voici comment on pourrait expliquer cette étape à un humain :
- Créons un dictionnaire vide nommé nombres.
- Lisons un par un les k couples (distance, catégorie) contenus dans la collection memoire
- Pour chaque enregistrement :
- si la clé n'existe pas encore dans nombres : on crée une clé ayant pour nom la catégorie de l'enregistrement et 1 pour valeur
- sinon, on incrémente de un la valeur associée à cette clé.
Un petit exemple pour compléter l'explication :
Premier enregistrement lu : (1.4142135623730951, 'Défenseur'),
memoire contient alors : {'Défenseur': 1}
Deuxième enregistrement lu : (2.0, 'Attaquant'),
memoire contient alors : {'Défenseur': 1, 'Attaquant': 1}
Troisième enregistrement lu : (2.23606797749979, 'Défenseur'),
memoire contient alors : {'Défenseur': 2, 'Attaquant': 1}
En version algorithme ça donne cela en utilisant les index pour réaliser la lecture des enregistrements :
⚐ Etape 3 ➡ on compte les catégories présentes
nombres ← Dictionnaire vide
index ← 0
TANT QUE index < k
categorie ← memoire[index][1]
SI la clé categorie existe déjà dans le dictionnaire nombres
nombres[categorie] ← nombres[categorie] + 1
SINON
nombres[categorie] ← 1
Fin du SI
Fin TANT QUE
Il va donc falloir savoir lire les éléments un par un sans les modifier en Python.
Ca, c'est facile et on sait le faire avec un index ou avec une lecture directe.
✎ 12° Créer un programme nommé questions.py qui contient les deux fonctions suivantes permettant de lire et afficher un par un les éléments.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 | memoire = [
(1.4142135623730951, 'Défenseur'),
(2.0, 'Attaquant'),
(2.23606797749979, 'Défenseur'),
(2.23606797749979, 'Milieu de terrain'),
(3.0, 'Défenseur'), (3.0, 'Défenseur'),
(3.605551275463989, 'Attaquant'),
(3.605551275463989, 'Attaquant'),
(3.605551275463989, 'Milieu de terrain'),
(4.123105625617661, 'Défenseur')
]
def lecture_par_index(tableau):
for index in range(len(tableau)):
print(tableau[index])
def lecture_par_element(tableau):
for element in tableau:
print(element)
|
Question : Puisqu'on ne va pas devoir modifier le contenu du tableau-collection, y-a-t-il une version qu'on ne doit pas utiliser ou peut-on utiliser l'une ou l'autre comme on veut ?
Vous pouvez vérifier le bon fonctionnement de vos fonctions en tapant cela par exemple :
>>> lecture_par_index(memoire)
(1.4142135623730951, 'Défenseur')
(2.0, 'Attaquant')
(2.23606797749979, 'Défenseur')
(2.23606797749979, 'Milieu de terrain')
(3.0, 'Défenseur')
(3.0, 'Défenseur')
(3.605551275463989, 'Attaquant')
(3.605551275463989, 'Attaquant')
(3.605551275463989, 'Milieu de terrain')
(4.123105625617661, 'Défenseur')
>>> lecture_par_element(memoire)
(1.4142135623730951, 'Défenseur')
(2.0, 'Attaquant')
(2.23606797749979, 'Défenseur')
(2.23606797749979, 'Milieu de terrain')
(3.0, 'Défenseur')
(3.0, 'Défenseur')
(3.605551275463989, 'Attaquant')
(3.605551275463989, 'Attaquant')
(3.605551275463989, 'Milieu de terrain')
(4.123105625617661, 'Défenseur')
Revenons à l'étape 3 de knn : il faut lire un par un les enregistrements dans memoire et créer une nouvelle clé dans un dictionnaire SI la clé n'existe pas encore.
Comment tester si une clé existe ou pas ?
En utilisant le mot clé in soit sur la variable-dictionnaire, soit sur la réponse de la méthode keys :
>>> nombres = {'Attaquant': 12, 'Défenseur': 20}
>>> 'Attaquant' in nombres
True
>>> 'Défenseur' in nombres
True
>>> 'Milieu de terrain' in nombres
False
>>> nombres = {'Attaquant': 12, 'Défenseur': 20}
>>> 'Attaquant' in nombres.keys()
True
>>> 'Défenseur' in nombres.keys()
True
>>> 'Milieu de terrain' in nombres.keys()
False
13° Remplacer gestion.py par ce nouveau programme (non finalisé). Lancer le programme. Lancer la ligne de commande présente sous le programme pour vérifier qu'il fonctionne. Nous analyserons son fonctionnement à la question suivante.
On notera que la fonction renvoie maintenant le tableau-collection nombres
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76 | # 1 - Importation
from creation_collection import creer_collection
from matplotlib import pyplot as plt
from math import sqrt
from operator import itemgetter
# 2 - Déclaration des fonctions
def distance(enr1, enr2):
"""Fonction qui renvoie la distance entre les deux enregistrements
:: param enr1 (dict) :: un dictionnaire correspondant à un enregistrement
:: param enr2 (dict) :: un dictionnaire correspondant à un enregistrement
:: return (float) :: la distance euclidienne entre les deux enregistrements
"""
x1 = enr1['Taille (cm)']
x2 = enr2['Taille (cm)']
y1 = enr1['Masse (kg)']
y2 = enr2['Masse (kg)']
d = sqrt( (x2-x1)**2 + (y2-y1)**2 )
return d
def knn(k, nouveau, collection):
"""Fonction qui renvoie la catégorie supposée de nouveau
:: param k(int) :: le nombre de plus proches voisins à gérer
:: param nouveau(dict) :: un enregistrement sans connaissance de la clé de catégorie
:: param collection(list) :: une collection d'enregistrements
:: return (list) :: un tableau contenant la ou les catégories majoritaires
"""
# Etape 1 - ajout de k couples (distance, catégorie) dans memoire
memoire = []
for index in range(k):
d = distance(nouveau, collection[index])
categorie = collection[index]['Poste']
memoire.append( (d,categorie) )
memoire.sort(key=itemgetter(0))
laPlusGrande = memoire[k-1][0]
# Etape 2 - on rajoute les autres au cas par cas
for index in range(k, len(collection)):
d = distance(nouveau, collection[index])
if d < laPlusGrande:
categorie = collection[index]['Poste']
memoire[k-1] = (d,categorie)
memoire.sort(key=itemgetter(0))
laPlusGrande = memoire[k-1][0]
# Etape 3 - on compte les catégories présentes dans memoire
nombres = {}
for enregistrement in memoire:
categorie = enregistrement[1]
if categorie in nombres:
nombres[categorie] = nombres[categorie] + 1
else:
nombres[categorie] = 1
return nombres
# 3 - Programme
if __name__ == '__main__':
# Collection : Création de la collection
joueurs = creer_collection("entrainement.csv")
# Collection : transformation en entiers des descripteurs numériques
for index in range(len(joueurs)):
joueurs[index]['Taille (cm)'] = int(joueurs[index]['Taille (cm)'])
joueurs[index]['Masse (kg)'] = int(joueurs[index]['Masse (kg)'])
enr_test = {'Poste':'X', 'Taille (cm)':182, 'Masse (kg)':75}
|
>>> knn(7, enr_test, joueurs)
Vous devriez avoir une réponse du type :
>>> knn(7, enr_test, joueurs)
{'Défenseur': 4, 'Attaquant': 2, 'Milieu de terrain': 1}
Que contient la variable memoire lors de ce calcul ?
[
(1.4142135623730951, 'Défenseur'),
(2.0, 'Attaquant'),
(2.23606797749979, 'Défenseur'),
(2.23606797749979, 'Milieu de terrain'),
(3.0, 'Défenseur'),
(3.0, 'Défenseur'),
(3.605551275463989, 'Attaquant')
]
Visiblement, cela fonctionne. Je vais maintenant vous posez quelques questions visant à savoir pourquoi...
✎ 14° Répondre aux questions ci-dessous liées à ce petit bout de la fonction knn.
Si cela vous aide à comprendre l'exécution du code, vous pouvez considérer que la collection-tableau memoire contient ceci :
memoire = [
(1.4142135623730951, 'Défenseur'),
(2.0, 'Attaquant'),
(2.23606797749979, 'Défenseur'),
(2.23606797749979, 'Milieu de terrain'),
(3.0, 'Défenseur'), (3.0, 'Défenseur'),
(3.605551275463989, 'Attaquant'),
(3.605551275463989, 'Attaquant'),
(3.605551275463989, 'Milieu de terrain'),
(4.123105625617661, 'Défenseur')
]
54
55
56
57
58
59
60
61
62 |
nombres = {}
for enregistrement in memoire:
categorie = enregistrement[1]
if categorie in nombres:
nombres[categorie] = nombres[categorie] + 1
else:
nombres[categorie] = 1
return nombres
|
Questions
- Ligne 54 : Quel est le type de la structure de données créée sur cette ligne : tableau, tuple(p-uplet) ou dictionnaire ?
- Ligne 55 : Quel est le type de la variable enregistrement sachant qu'il s'agit de lire le contenu de la collection-tableau memoire ?
- Ligne 55 - QCM : on considère qu'il s'agit du premier passage avec la variable memoire donnée en exemple. Que contient enregistrement sur ce premier passage :
- A : le tableau-collection
memoire - B : le tuple
(1.4142135623730951, 'Défenseur') - C : le float
1.4142135623730951, c'est à dire l'élément 0 du tuple précédent. - D : le string
'Défenseur', c'est à dire l'élément 1 du tuple précédent. - Ligne 56 - QCM : on considère qu'il s'agit du premier passage avec la variable memoire donnée en exemple. Que contient categorie sur ce premier passage :
- A : le tableau-collection
memoire - B : le tuple
(1.4142135623730951, 'Défenseur') - C : le float
1.4142135623730951, c'est à dire l'élément 0 du tuple précédent. - D : le string
'Défenseur', c'est à dire l'élément 1 du tuple précédent. - Ligne 57 - QCM : Quelle est la phrase qui correspond à ce que fait cette ligne de code :
- A : Si la clé categorie est présente dans le dictionnaire nombres
- B : Si l'index categorie est présente dans le dictionnaire nombres
- C : Si la valeur categorie est présente dans le dictionnaire nombres
- D : Si la clé categorie est bien un nombre
- Lignes 57 à 60 : A quoi servent globalement ces lignes ?
15° Compléter le contenu mis à jour au fur et à mesure des passages dans la boucle du dictionnaire nombres.
memoire = [
(1.4142135623730951, 'Défenseur'),
(2.0, 'Attaquant'),
(2.23606797749979, 'Défenseur'),
(2.23606797749979, 'Milieu de terrain'),
(3.0, 'Défenseur'), (3.0, 'Défenseur'),
(3.605551275463989, 'Attaquant'),
(3.605551275463989, 'Attaquant'),
(3.605551275463989, 'Milieu de terrain'),
(4.123105625617661, 'Défenseur')
]
Avant
Boucle 1
Boucle 2
Boucle 3
Boucle 4
Boucle 5
Boucle 6
Boucle 7 | {}
{'Défenseur': 1}
{'Défenseur': 1, 'Attaquant': 1}
{'Défenseur': 2, 'Attaquant': 1}
{'Défenseur': 2, 'Attaquant': 1, 'Milieu de terrain': 1}
?
??
???
|
...CORRECTION...
Avant
Boucle 1
Boucle 2
Boucle 3
Boucle 4
Boucle 5
Boucle 6
Boucle 7 | {}
{'Défenseur': 1}
{'Défenseur': 1, 'Attaquant': 1}
{'Défenseur': 2, 'Attaquant': 1}
{'Défenseur': 2, 'Attaquant': 1, 'Milieu de terrain': 1}
{'Défenseur': 3, 'Attaquant': 1, 'Milieu de terrain': 1}
{'Défenseur': 4, 'Attaquant': 1, 'Milieu de terrain': 1}
{'Défenseur': 4, 'Attaquant': 2, 'Milieu de terrain': 1}
|
Voyons voir l'influence du choix de k sur la réponse fournie par l'algorithme :
16° Lancer la commande ci-dessous dans la console (les différentes fonctions et variables doivent bien entendu être en mémoire au préalable).
>>> for k in range(7,38,5) : print(k, ' : ', knn(k, enr_test, joueurs))
Question : le choix de la valeur de k influe-t-il sur la réponse donnée ?
...CORRECTION...
Le choix de k va effectivement avoir une influence sur la réponse : plus on considère de proches voisins, plus on s'éloigne du point de base. Si on va trop loin, on finit éventuellement par trouver plus d'une catégorie qu'une autre.
Voici à titre d'exemple les réponses fournies de k = 1 à k = 30.
Nous verrons dans la dernière partie de ce cours comment on peut tenter de trouver une valeur optimale de k.
1 : {'Défenseur': 1}
2 : {'Défenseur': 1, 'Attaquant': 1}
3 : {'Défenseur': 2, 'Attaquant': 1}
4 : {'Défenseur': 2, 'Attaquant': 1, 'Milieu de terrain': 1}
5 : {'Défenseur': 3, 'Attaquant': 1, 'Milieu de terrain': 1}
6 : {'Défenseur': 4, 'Attaquant': 1, 'Milieu de terrain': 1}
7 : {'Défenseur': 4, 'Attaquant': 2, 'Milieu de terrain': 1}
8 : {'Défenseur': 4, 'Attaquant': 3, 'Milieu de terrain': 1}
9 : {'Défenseur': 4, 'Attaquant': 3, 'Milieu de terrain': 2}
10 : {'Défenseur': 5, 'Attaquant': 3, 'Milieu de terrain': 2}
11 : {'Défenseur': 5, 'Attaquant': 3, 'Milieu de terrain': 3}
12 : {'Défenseur': 5, 'Attaquant': 4, 'Milieu de terrain': 3}
13 : {'Défenseur': 5, 'Attaquant': 4, 'Milieu de terrain': 3, 'Gardien': 1}
14 : {'Défenseur': 5, 'Attaquant': 4, 'Milieu de terrain': 3, 'Gardien': 2}
15 : {'Défenseur': 5, 'Attaquant': 5, 'Milieu de terrain': 3, 'Gardien': 2}
16 : {'Défenseur': 5, 'Attaquant': 6, 'Milieu de terrain': 3, 'Gardien': 2}
17 : {'Défenseur': 6, 'Attaquant': 6, 'Milieu de terrain': 3, 'Gardien': 2}
18 : {'Défenseur': 6, 'Attaquant': 6, 'Milieu de terrain': 4, 'Gardien': 2}
19 : {'Défenseur': 7, 'Attaquant': 6, 'Milieu de terrain': 4, 'Gardien': 2}
20 : {'Défenseur': 7, 'Attaquant': 6, 'Milieu de terrain': 4, 'Gardien': 3}
21 : {'Défenseur': 7, 'Attaquant': 6, 'Milieu de terrain': 5, 'Gardien': 3}
22 : {'Défenseur': 7, 'Attaquant': 7, 'Milieu de terrain': 5, 'Gardien': 3}
23 : {'Défenseur': 7, 'Attaquant': 7, 'Milieu de terrain': 5, 'Gardien': 4}
24 : {'Défenseur': 7, 'Attaquant': 7, 'Milieu de terrain': 6, 'Gardien': 4}
25 : {'Défenseur': 8, 'Attaquant': 7, 'Milieu de terrain': 6, 'Gardien': 4}
26 : {'Défenseur': 8, 'Attaquant': 7, 'Milieu de terrain': 7, 'Gardien': 4}
27 : {'Défenseur': 9, 'Attaquant': 7, 'Milieu de terrain': 7, 'Gardien': 4}
28 : {'Défenseur': 9, 'Attaquant': 8, 'Milieu de terrain': 7, 'Gardien': 4}
29 : {'Défenseur': 9, 'Attaquant': 9, 'Milieu de terrain': 7, 'Gardien': 4}
30 : {'Défenseur': 9, 'Attaquant': 10, 'Milieu de terrain': 7, 'Gardien': 4}
6 - Etape finale 4 en Python
Nous avons avancé : on obtient maintenant les nombres de voisins par catégorie, stockés dans un dictionnaire nommé nombres.
Un exemple de contenu possible avec un seul gagnant :
{'Défenseur': 9, 'Attaquant': 10, 'Milieu de terrain': 7, 'Gardien': 4}
Un autre exemple avec deux catégories majoritaires :
{'Défenseur': 6, 'Attaquant': 6, 'Milieu de terrain': 4, 'Gardien': 2}
Reste à automatiser la réponse : trouver la ou les réponses les plus nombreuses.
Pour cela, nous allons lire le dictionnaire nombres par clé ou par valeur de façon à trouver la valeur maximale.
Nous avons noté ceci dans l'algorithme :
⚐ Etape 4 : on renvoie la catégorie majoritaire
reponse ← cleMajoritaire(nombres)
Renvoyer reponse
L'algorithme cachait donc cette étape dans la fonction cleMajoritaire. Son boulot ? Renvoyer la catégorie la plus marquée parmi les k catégories enregistrées dans nombre.
Avec Python, on peut obtenir les couples (cle, valeur) en utilisant la méthode items.
Méthode items
La méthode des dictionnaires items permet de créer un ensemble contenant des tuples : les clés du dictionnaire ET leurs valeurs associées. On pourra ainsi lire une à une clé et valeur avec une boucle for.
1
2
3 | nombres = {'Défenseur': 9, 'Attaquant': 10, 'Milieu de terrain': 7, 'Gardien': 4}
for (cle, valeur) in nombres.items():
print(f"La clé {cle} est associée à la valeur {valeur}.")
|
En lançant ce programme, on obtient ceci :
La clé Défenseur est associée à la valeur 9.
La clé Attaquant est associée à la valeur 10.
La clé Milieu de terrain est associée à la valeur 7.
La clé Gardien est associée à la valeur 4.
Vous allez maintenant devoir utiliser cette méthode pour parvenir à renvoyer la catégorie majoritaire.
✎ 17° Compléter l'étape 4 de la fonction knn pour qu'elle joue le rôle de la fonction cleMajoritaire : on doit lire une à une les valeurs dans le dictionnaire nombres et placer au final la clé majoritaire dans la variable reponse.
Le code complet est fourni en dessous. Voici l'extrait à compléter.
62
63
64
65
66
67
68 |
# Etape 4 - on cherche la catégorie majoritaire
reponse = None
maximum = 0
for cle, valeur in nombres.items():
if valeur > maximum:
pass
return reponse
|
Il s'agit de l'exercice typique de la recherche séquentielle de la valeur maximale. La seule différence est qu'on cherche à renvoyer la clé (qui est la catégorie) et pas la valeur
- si la valeur est plus grande que le maximum stocké,
- on place la valeur dans maximum et
- on place la clé-catégorie dans réponse.
A vous de jouer. Si vous ne trouvez pas la réponse, vous pourrez utiliser la correction de la question 18 qui intègre un cas plus complexe.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82 | # 1 - Importation
from creation_collection import creer_collection
from matplotlib import pyplot as plt
from math import sqrt
from operator import itemgetter
# 2 - Déclaration des fonctions
def distance(enr1, enr2):
"""Fonction qui renvoie la distance entre les deux enregistrements
:: param enr1 (dict) :: un dictionnaire correspondant à un enregistrement
:: param enr2 (dict) :: un dictionnaire correspondant à un enregistrement
:: return (float) :: la distance euclidienne entre les deux enregistrements
"""
x1 = enr1['Taille (cm)']
x2 = enr2['Taille (cm)']
y1 = enr1['Masse (kg)']
y2 = enr2['Masse (kg)']
d = sqrt( (x2-x1)**2 + (y2-y1)**2 )
return d
def knn(k, nouveau, collection):
"""Fonction qui renvoie la catégorie supposée de nouveau
:: param k(int) :: le nombre de plus proches voisins à gérer
:: param nouveau(dict) :: un enregistrement sans connaissance de la clé de catégorie
:: param collection(list) :: une collection d'enregistrements
:: return (list) :: un tableau contenant la ou les catégories majoritaires
"""
# Etape 1 - ajout de k couples (distance, catégorie) dans memoire
memoire = []
for index in range(k):
d = distance(nouveau, collection[index])
categorie = collection[index]['Poste']
memoire.append( (d,categorie) )
memoire.sort(key=itemgetter(0))
laPlusGrande = memoire[k-1][0]
# Etape 2 - on rajoute les autres au cas par cas
for index in range(k, len(collection)):
d = distance(nouveau, collection[index])
if d < laPlusGrande:
categorie = collection[index]['Poste']
memoire[k-1] = (d,categorie)
memoire.sort(key=itemgetter(0))
laPlusGrande = memoire[k-1][0]
# Etape 3 - on compte les catégories présentes dans memoire
nombres = {}
for enregistrement in memoire:
categorie = enregistrement[1]
if categorie in nombres:
nombres[categorie] = nombres[categorie] + 1
else:
nombres[categorie] = 1
# Etape 4 - on cherche la catégorie majoritaire
reponse = None
maximum = 0
for cle, valeur in nombres.items():
if valeur > maximum:
pass
return reponse
# 3 - Programme
if __name__ == '__main__':
# Collection : Création de la collection
joueurs = creer_collection("entrainement.csv")
# Collection : transformation en entiers des descripteurs numériques
for index in range(len(joueurs)):
joueurs[index]['Taille (cm)'] = int(joueurs[index]['Taille (cm)'])
joueurs[index]['Masse (kg)'] = int(joueurs[index]['Masse (kg)'])
enr_test = {'Poste':'X', 'Taille (cm)':182, 'Masse (kg)':75}
|
Vous avez réalisé une version complète de l'algorithme knn !
La solution réalisée pour cette question 17 ne peut renvoyer qu'une seule catégorie. Or que faire si 'Attaquant' et 'Défenseur' apparaissent 20 fois chacun ?
Et bien, on pourrait décider de renvoyer systématiquement un tuple :
- Une seule catégorie en sortie ? On renvoie le tuple
('Attaquant',) - Plusieurs catégories en sortie ? On renvoie le tuple
('Attaquant', 'Défenseur')
Le principe de la solution proposée est simple mais contient une spécificité des tuples : un tuple + un tuple renvoie un tuple contenant les éléments des deux tuples précédents. Notez bien la présence de la virgule pour signaler qu'on veut créer un tuple dans l'exemple ci-dessous.
>>> reponse = ('Défenseur',)
>>> reponse
('Défenseur',)
>>> reponse = reponse + ('Attaquant',)
>>> reponse
('Défenseur', 'Attaquant')
La solution finale proposée utilise donc cette astuce de cette manière :
63
64
65
66
67
68
69
70
71 |
reponse = None
maximum = 0
for cle, valeur in nombres.items():
if valeur > maximum:
reponse = (cle,)
maximum = valeur
elif valeur == maximum:
reponse = reponse + (cle,)
return reponse
|
- On place systématiquement un tuple dans reponse.
- Ligne 66 ci-dessous : Si la valeur est bien un nouveau maximum : on place dans reponse un tuple ne contenant qu'un seul élément.
- Ligne 69 ci-dessous : Si la valeur est égale au maximum, on la rajoute sous forme d'un tuple dans le tuple reponse
18° Utiliser le code suivant pour modifier une dernière fois notre fonction knn : l'étape 4 intégre maintenant les réponses multiples : on renvoie toujours un tuple qui contient parfois une réponse (exemple ('Défenseur',) ), parfois plusieurs (exemple ('Défenseur', 'Attaquant') ).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85 | # 1 - Importation
from creation_collection import creer_collection
from matplotlib import pyplot as plt
from math import sqrt
from operator import itemgetter
# 2 - Déclaration des fonctions
def distance(enr1, enr2):
"""Fonction qui renvoie la distance entre les deux enregistrements
:: param enr1 (dict) :: un dictionnaire correspondant à un enregistrement
:: param enr2 (dict) :: un dictionnaire correspondant à un enregistrement
:: return (float) :: la distance euclidienne entre les deux enregistrements
"""
x1 = enr1['Taille (cm)']
x2 = enr2['Taille (cm)']
y1 = enr1['Masse (kg)']
y2 = enr2['Masse (kg)']
d = sqrt( (x2-x1)**2 + (y2-y1)**2 )
return d
def knn(k, nouveau, collection):
"""Fonction qui renvoie la catégorie supposée de nouveau
:: param k(int) :: le nombre de plus proches voisins à gérer
:: param nouveau(dict) :: un enregistrement sans connaissance de la clé de catégorie
:: param collection(list) :: une collection d'enregistrements
:: return (tuple) :: un tuple contenant la ou les catégories majoritaires
"""
# Etape 1 - ajout de k couples (distance, catégorie) dans memoire
memoire = []
for index in range(k):
d = distance(nouveau, collection[index])
categorie = collection[index]['Poste']
memoire.append( (d,categorie) )
memoire.sort(key=itemgetter(0))
laPlusGrande = memoire[k-1][0]
# Etape 2 - on rajoute les autres au cas par cas
for index in range(k, len(collection)):
d = distance(nouveau, collection[index])
if d < laPlusGrande:
categorie = collection[index]['Poste']
memoire[k-1] = (d,categorie)
memoire.sort(key=itemgetter(0))
laPlusGrande = memoire[k-1][0]
# Etape 3 - on compte les catégories présentes dans memoire
nombres = {}
for enregistrement in memoire:
categorie = enregistrement[1]
if categorie in nombres:
nombres[categorie] = nombres[categorie] + 1
else:
nombres[categorie] = 1
# Etape 4 - on cherche la catégorie majoritaire
reponse = None
maximum = 0
for cle, valeur in nombres.items():
if valeur > maximum:
reponse = (cle,)
maximum = valeur
elif valeur == maximum:
reponse = reponse + (cle,)
return reponse
# 3 - Programme
if __name__ == '__main__':
# Collection : Création de la collection
joueurs = creer_collection("entrainement.csv")
# Collection : transformation en entiers des descripteurs numériques
for index in range(len(joueurs)):
joueurs[index]['Taille (cm)'] = int(joueurs[index]['Taille (cm)'])
joueurs[index]['Masse (kg)'] = int(joueurs[index]['Masse (kg)'])
enr_test = {'Poste':'X', 'Taille (cm)':182, 'Masse (kg)':75}
|
Lancer ensuite le code fourni dans la console.
>>> for k in range(1,40,1) : print(k, ' : ', knn(k, enr_test, joueurs))
Et voici les réponses de l'algorithme en fonction de k :
1 : ('Défenseur',)
2 : ('Défenseur', 'Attaquant')
3 : ('Défenseur',)
4 : ('Défenseur',)
5 : ('Défenseur',)
6 : ('Défenseur',)
7 : ('Défenseur',)
8 : ('Défenseur',)
9 : ('Défenseur',)
10 : ('Défenseur',)
11 : ('Défenseur',)
12 : ('Défenseur',)
13 : ('Défenseur',)
14 : ('Défenseur',)
15 : ('Défenseur', 'Attaquant')
16 : ('Attaquant',)
17 : ('Défenseur', 'Attaquant')
18 : ('Défenseur', 'Attaquant')
19 : ('Défenseur',)
20 : ('Défenseur',)
21 : ('Défenseur',)
22 : ('Défenseur', 'Attaquant')
23 : ('Défenseur', 'Attaquant')
24 : ('Défenseur', 'Attaquant')
25 : ('Défenseur',)
26 : ('Défenseur',)
27 : ('Défenseur',)
28 : ('Défenseur',)
29 : ('Défenseur', 'Attaquant')
30 : ('Attaquant',)
31 : ('Défenseur', 'Attaquant')
32 : ('Défenseur', 'Attaquant')
33 : ('Défenseur', 'Attaquant')
34 : ('Défenseur', 'Attaquant', 'Milieu de terrain')
35 : ('Attaquant',)
36 : ('Défenseur', 'Attaquant')
37 : ('Attaquant',)
38 : ('Attaquant',)
39 : ('Attaquant', 'Milieu de terrain')
7 - FAQ
Est-on obligé d'envoyer des p-uplets dans le tableau-collection mémoire ?
Nous avions écrit ceci :
memoire[k-1] = (d,categorie)
On stocke donc des enregistrements sous forme de tuples car la distance est un flottant et la catégorie est un string.
Par contre, les tableaux de Python ne sont pas de vrais tableaux : les éléments peuvent être de nature différentes. On pourra donc écrire également cela en Python :
memoire[k-1] = [d,categorie]
Attention néanmoins : malgré la présence des crochets, il ne s'agit pas d'un 'vrai' tableau mais d'un objet list-Python qu'on utilise comme un tableau.
Activité publiée le 30 05 2020
Dernière modification : 02 04 2023
Auteur : ows. h.