Implémentation correcte ?
Pour que l'implémentation soit qualifiée de "correcte", il faut que les opérations primitives aient un coût "faible".
12 - Implémenter une Liste 1/3
Aujourd'hui, nous allons implémenter une Liste Récursive (Tête, Queue) sous forme d'une structure de données nommée Liste Chaînée.
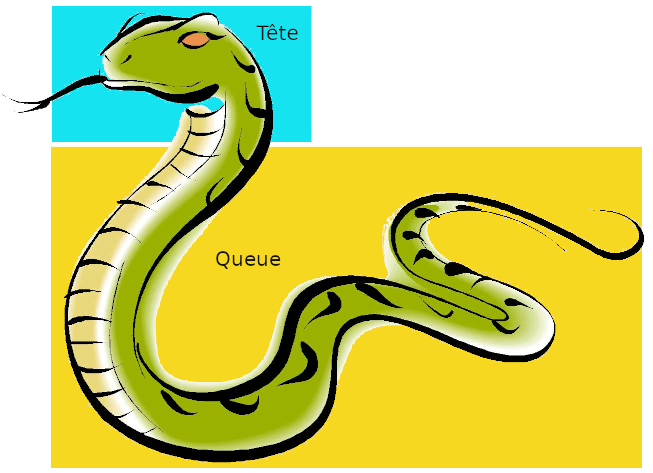
Version du vocabulaire utilisé ici :
- TETE : la première Place d'une Liste.
- QUEUE : l'ensemble des autres Places d'une Liste.
- FIN : la dernière Place d'une Liste.
Prerequis : l'activité sur les Listes.
Documents de cours : open document ou pdf
1 - Liste chainée sous forme de tuples
1.1 - Liste Chaînée
(Rappel) Idée Abstraite : Liste Récursive
Une Liste Récursive est une Liste qu'on doit explorer de proche en proche en partant de la tête.
Implémentation possible : la Liste Chaînée
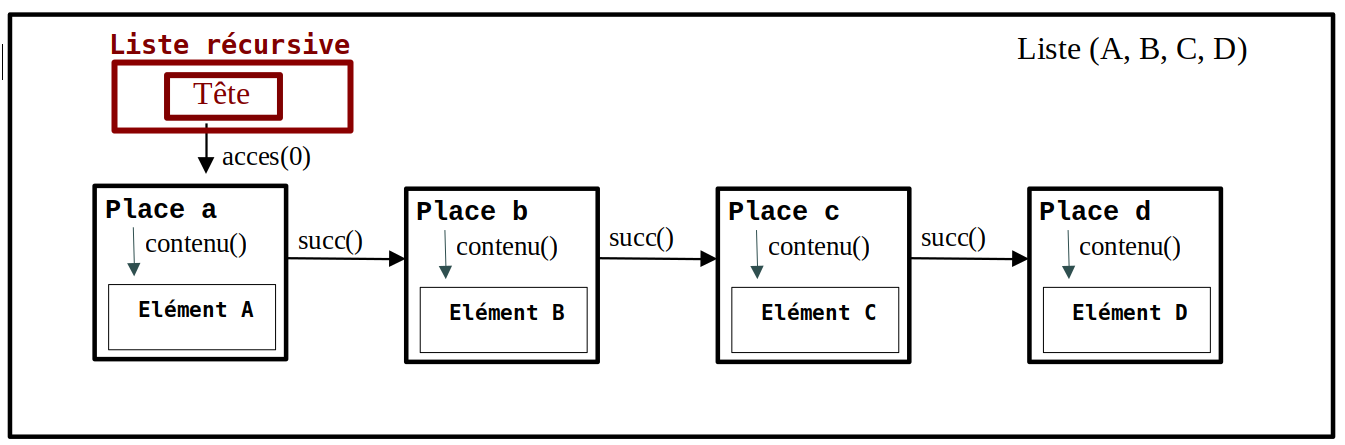
Une bonne manière d'implémenter une Liste Récursive est d'utiliser une Liste Chaînée.
Les Places sont implémentées sous forme de Cellules : des structures comportant au moins deux informations :
- l'Elément qu'elle stocke et
- une référence menant au Successeur.
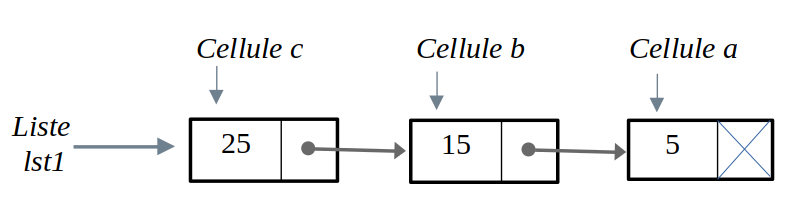
On notera donc que le Successeur est soit une Cellule, soit une référence VIDE.
Successeur = Cellule|VIDE
La Liste NON VIDE est alors une structure de donnés comportant au moins une information : l'adresse de sa tête.
1.2 - Implémentation précise choisie : liste chaînée tuple (tête, queue)
Les choix effectués ont pour but de créer une liste chaînée valide mais simple.
A - Implémentation des Cellules sous forme de tuples (Element, successeur)
Les Cellules seront implémentées par un tuple à deux emplacements (nommé également couple ou 2-uplet) :
Cellule = (Element, Successeur) par définition (de Cellule)
Cellule = (Element, Cellule|VIDE) par définition (de Successeur)
Puisque Cellule est un tuple, on décide d'implémenter VIDE comme un tuple également, le tuple vide ().
Cellule = (Element, Cellule|()) pour cette implémentation.
Voici comment extraire les deux informations du couple :
Cellule[0] -> Element
Cellule[1] -> Cellule|()
B - Implémentation de la Liste comme un simple alias vers la tête
La Liste Chaînée ne comportera qu' une information : où se trouve le début. On stockera l'information comme un simple alias : une variable lst1 référençant la liste va donc pointer exactement la même zone mémoire qu'une variable c qui pointerait en mémoire sur la cellule de tête.
Voici un exemple de création de liste non vide :
>>> c = (25, (15, (5, ()))
>>> lst1 = c
Deux cas : soit la Liste est NON VIDE (et le début est une Cellule), soit la liste est VIDE (et il n'y a pas de début !)
Liste = Liste NON VIDE | Liste VIDE par définition.
Liste = Cellule | Liste VIDE pour cette implémentation.
Puisque Liste NON VIDE est un alias vers une Cellule qui est un tuple, on décide d'implémenter Liste VIDE comme un tuple, le tuple vide ().
Liste = Cellule|() pour cette implémentation.
1.3 - Manipulation des Cellules en Python
Cellule = (Element, Cellule|())
A - Successeur VIDE
L'absence de Successeur est implémenté par un tuple vide.
Notez bien qu'une Cellule ne peut pas être vide. C'est la référence vers un Successeur qui peut manquer.
>>> VIDE = ()
B - Cellule comme un tuple (Elément, Successeur)
Créons une Cellule a qui contient 5 et n'a pas de successeur.
>>> a = (5, ())
>>> a
(5, ())
Une Cellule a contient deux informations :
- a[0] : l'Elément stocké (5 ici),
- a[1] : le Successeur qui peut être soit (), soit une autre Cellule (ici, on lit ())
C - Insérer une Cellule devant une autre
Très facile : on crée un nouveau tuple qui contient le nouvel élément et on a fait de l'autre cellule son Successeur.
>>> a = (5, ())
>>> b = (15, a)
>>> b
(15, (5, ()))
>>> c = (25, b)
>>> c
(25, (15, (5, ())))
D'abord, on crée une Cellule b qui contient 15 et dont le successeur est la cellule a.
Ensuite, on crée une Cellule c qui contient 25 et dont le successeur est la cellule b.
D - Lire l'Element contenu dans une Cellule
Connaissant la référence d'une Cellule c, il est facile de trouver son Elément : c'est l'indice 0.
>>> c
(25, (15, (5, ())))
>>> c[0]
25
La Cellule c contient 25.
E - Lire le successeur
Il suffit de récupérer l'indice 1 de la Cellule.
>>> c
(25, (15, (5, ())))
>>> s = c[1]
>>> s
(15, (5, ()))
Le successeur de la Cellule c est une Cellule contenant 25 et qui mène elle-même à une cellule qui contient 15, ...
1.4 Manipulation de la Liste Chaînée (tête, queue) minimaliste en Python
A - Liste VIDE
On a fait le choix de représenter une Liste VIDE par un tuple vide ().
>>> lst1 = ()
B - Liste NON VIDE
La variable d'une telle liste n'est qu'un alias de la Cellule de tête : ci-dessous, lst1 et c pointent vers la même zone mémoire : un tuple.
>>> c
(25, (15, (5, ())))
>>> lst1 = c
>>> lst1
(25, (15, (5, ())))
lst1 et c référencent donc le même contenu.
C - Insérer une Tête
Très facile : on crée une nouvelle Liste dont l'indice 0 est le nouvel élément et l'indice 1 est la Queue de notre Liste.
>>> lst2 = (50, lst1)
>>> lst2
(50, (25, (15, (5, ()))))
lst2 est une Liste NON VIDE dont la tête contient 50 et dont la queue est la liste lst1.
D - Récupérer la valeur de tête
Connaissant lst1, il est assez facile de trouver son Elément : il est sur l'indice 0 du tuple.
>>> lst1
(25, (15, (5, ())))
>>> lst1[0]
25
La liste NON VIDE lst1 est une liste dont la tête contient 25.
E - Supprimer la tête, c'est à dire extraire la queue
Puisque la structure de données est immuable, supprimer la tête revient à récupérer la queue.
Il suffit de récupérer l'indice 1 du tuple-Liste.
>>> lst1
(25, (15, (5, ())))
>>> q = lst1[1]
>>> q
(15, (5, ()))
La liste NON VIDE q est la queue de la liste NON VIDE lst1.
1.5 - Ambigüité de la "Liste Chaînée Tuple (Tête, Queue)"
Vous devriez avoir constaté qu'il n'y avait pas de différence de traitement au niveau du code entre gestion des Cellules et gestion des Listes lorsqu'elles sont non vides... Pourquoi ?
A - Justification mathématique de cette ambigüité
Liste = Liste NON VIDE | Liste VIDE
Liste = Cellule | ()
On voit donc que dans cette implémentation précise, il n'y a pas de différence réelle entre une Cellule et une Liste NON VIDE. Pourtant, au niveau abstrait, il s'agit bien de deux notions différentes :
- La Liste représente le meuble de rangement.
- La Cellule représente l'un des dossiers suspendus dans le meuble.
B - Interpréter un contenu interne
Dans cette implémentation, il n'existe pas de réelle différence entre manipuler une Liste NON VIDE et une Cellule alors même que du point de vue abstrait Liste et Place représentent bien deux concepts différents.
Un exemple : pourriez-vous dire si y est une Liste ou une Cellule ?
>>> x = ("o", ("n", ()))
>>> y = ("B", x)
>>> y
("B", ("o", ("n", ())))
Réponse : non. On peut comprendre le tuple y de deux façons
y est une Cellule contenant "B" et dont le successeur est la Cellule x.
y est une Liste Chaînée NON VIDE dont la valeur de tête est "B" et dont la Queue est la Liste Chaînée x.
C - Avantage ou désavantage ?
Avantage : la simplicité de notre implémentation la rend plutôt solide et facile à coder.
Désavantage : si vous voulez un jour rajouter des informations dans votre Liste (longueur, adresse de sa Fin...), vous allez coincer car vous ne distinguez pas Liste et Cellule.
Vous allons maintenant réaliser les fonctions d'interface permettant de créer cette structure de données.
Une fois que les 7 opérations primitives auront été créées, vous compléterez l'interface de façon à offrir les fonctions manquantes et vous pourrez voir qu'on peut effectivement la qualifier de Liste.
Nous aurons alors un beau module qui nous permettra d'utiliser des Listes Chaînées Immuables et donc de pouvoir programmer facilement les algorithmes qui sont décrits en manipulant une Liste Récursive.
Le MODULE version 1 : PRIMITIVES de la liste_chainee_ttq IMMUABLE de ce TP
Ci-dessous vous trouverez le module non finalisé implémentant une "Liste Chaînée tuple (Tête, Queue)".
Les Places portent le nom de Cellules dans ce type d'implémentation.
On notera que fournir premier() va permettre de manipuler notre liste sans se soucier des Cellules directement. C'est pour cela que acces_tete(), contenu() et successeur() sont grisées : elles existent mais premier() permet de s'en passer.
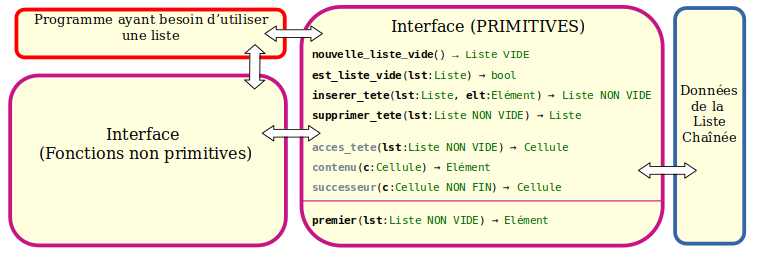
Voici les primitives qu'on sélectionne classiquement pour manipuler une Liste chaînée :
- nouvelle_liste_vide() → Liste VIDE
- est_liste_vide(lst:Liste) → bool
- inserer_tete(lst:Liste, elt:Element) → Liste NON VIDE
- supprimer_tete(lst:Liste NON VIDE) → Liste
- premier(lst:Liste NON VIDE) → Elément
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123 | |
01° Enregistrer ce module en le nommant bien liste_chainee_tq.py, sans accent attention.
Lancer le module directement.
Questions
- Que vont renvoyer ces instructions ?
- Quelle est l'instruction qui utilise bien l'interface proposée : A ou B ?
- Quelle est l'instruction qui manipule directement les données sans passer par l'interface : A ou B ?
- L'utilisateur d'un module est-il sensé savoir comment les données sont réellement implémentées ?
Instruction A
>>> a = ()
>>> est_liste_vide(a)
???
Instruction B
>>> b = nouvelle_liste_vide()
>>> est_liste_vide(b)
???
...CORRECTION...
Question 1
>>> a = ()
>>> est_liste_vide(a)
True
>>> b = nouvelle_liste_vide()
>>> est_liste_vide(b)
True
Question 2
b respecte l'interface.
Question 3
Avec a, on crée une liste sans passer par la fonction d'interface nouvelle_liste_vide(). Cette manipulation directe implique qu'on manipule directement les données.
Question 4
L'utilisateur n'est pas sensé manipuler les données internes du module : il doit utiliser uniquement les fonctions d'interface qu'on lui a fourni. De cette façon, ses programmes resteront fonctionnels même si les créateurs du module changent légèrement la gestion interne après une mise à jour.
02° Modifier la fonction d'interface inserer_tete() qui ne répond pas ce qu'il faut pour le moment.
Une fois fois que vous pensez avoir trouvé, testez votre résultat en activant la fonction de tests intégrée au module :
>>> tester_inserer_tete()
Prototype
def inserer_tete(lst:'Liste', elt:'Element') -> 'Liste NON VIDE':
Exemple d'utilisation
>>> a = nouvelle_liste_vide()
>>> a
()
>>> a = inserer_tete(a, 5)
>>> a
(5, ())
>>> a = inserer_tete(a, 2)
>>> a
(2, (5, ()))
Aide
Il suffit de renvoyer un nouveau tuple (élément de tête, queue) dont
- L'élément de tête est notre elt et
- La queue est la liste initiale lst.
...CORRECTION...
1
2
3 | |
Dans LISP
Historiquement, dans LISP cette fonction inserer_tete() se nomme cons() (comme _cons_truct).
03° Modifier la fonction d'interface supprimer_tete() qui ne renvoie pas la réponse attendue pour le moment.
Prototype
def supprimer_tete(lst:'Liste NON VIDE') -> 'Liste':
Spécifications
supprimer_tete(lst:Liste NON VIDE) -> Liste
Renvoie une nouvelle liste où la tête est maintenant la tête de la queue de lst.
Précondition : lst est une liste NON VIDE. Inutile donc gérer les cas où on vous envoie une liste vide, ou pire : un truc qui n'est pas une liste. Ce n'est pas votre problème en tant que concepteur de cette fonction.
Voici quelques exemples d'utilisation :
>>> a = nouvelle_liste_vide()
>>> a = inserer_tete(nouvelle_liste_vide(), 5)
>>> a
(5, ())
>>> b = supprimer_tete(a)
>>> b
()
>>> a = (20, (15, (5, ())))
>>> a
(20, (15, (5, ())))
>>> b = supprimer_tete(a)
>>> b
(15, (5, ()))
>>> a
(20, (15, (5, ())))
AIDE : on aurait pu nommer cette fonction recupererQueue() puisque c'est ce qu'elle fait.
Fonction de test
>>> tester_supprimer_tete()
...CORRECTION...
1
2
3 | |
04° Passons aux fonctions acces_tete(), contenu() et successeur() manipulant les Cellules. Dans cette implémentation, elles n'ont pas vraiment de raison d'être puisque les Cellules et les Listes NON VIDES sont gérées de la même façon. Puisque nous avons déjà de quoi gérer les Listes, nous pourrions presque nous passer de ces fonctions.
- Expliquer pourquoi, dans cette implémentation, la fonction acces_tete() renvoie effectivement la Cellule de tête avec l'instruction return lst de la ligne 40.
- Modifier la primitive contenu() pour qu'elle fonctionne.
- Modifier la primitive successeur() pour qu'elle renvoie bien le successeur de la Cellule c.
38
39
40
41
42
43
44
45
46
47
48 | |
Fonctions de test
>>> tester_acces_tete()
>>> tester_contenu()
>>> tester_successeur()
...CORRECTION...
Question 1
Dans cette implémentation, nous avions remarqué qu'une Liste NON VIDE n'est finalement qu'un alias de la Cellule de tête. La liste et sa Cellule de tête pointent donc la même zone mémoire : il s'agit des mêmes données avec deux noms pour les atteindre.
Questions 2-3
39
40
41
42
43
44
45
46
47
48
49 | |
05-A° Il est assez pénible d'accéder à la valeur stockée dans la Cellule de Tête pour l'instant : il faut d'abord utiliser la fonction acces_tete() puis utiliser contenu().
valeur_de_tete = contenu(acces_tete(lst))
Réaliser la fonction premier() qui renvoie directement l'Elément stocké en tête d'une Liste NON VIDE. Lors de cette réalisation, on vous demande ici de manipuler directement les données de la liste sans passer par les autres opérations primitives.
Prototype
def premier(lst:'Liste NON VIDE') -> 'Element':
Spécification
premier(lst:Liste NON VIDE) -> Element
Renvoie la valeur en tête de la liste lst.
PRECONDITION : La Liste ne doit PAS ETRE VIDE.
Exemple d'utilisation
>>> a = inserer_tete(nouvelle_liste_vide(), 5)
>>> a = inserer_tete(a, 15)
>>> premier(a)
15
>>> b = nouvelle_liste_vide()
>>> premier(b)
IndexError: tuple index out of range
...CORRECTION...
1
2
3 | |
05-B° Même question, mais en utilisant les autres primitives plutôt que de manipuler directement le tuple.
...CORRECTION...
1
2
3 | |
05-C° On considère que l'implémentation des tuples dans Python permet de
- lire un tuple à coût constant
- lire le contenu d'une case d'un tuple à coût constant.
En étudiant les instructions de notre implémentation de liste, répondre mentalement aux questions suivantes puis regarder les corrections pour voir si vous aviez raison :
- Quel est le coût de nouvelle_liste_vide() ?
- Quel est le coût de est_liste_vide() ?
- Quel est le coût de inserer_tete() ?
- Quel est le coût de supprimer_tete() ?
- Quel est le coût de acces_tete() ?
- Quel est le coût de contenu() ?
- Quel est le coût de successeur() ?
- Quel est le coût de premier() version 5A ?
- Quel est le coût de premier() version 5B ?
- Quelle est la version de premier() à privilégier ?
...CORRECTION...
- Quel est le coût de nouvelle_liste_vide() ?
- Quel est le coût de est_liste_vide() ?
- Quel est le coût de inserer_tete() ?
- Quel est le coût de supprimer_tete() ?
- Quel est le coût de acces_tete() ?
- Quel est le coût de contenu() ?
- Quel est le coût de successeur() ?
- Quel est le coût de premier() version 5A ?
- Quel est le coût de premier() version 5B ?
- Quelle est la version de premier() à privilégier ?
On renvoie juste un tuple. Le coût est donc constant.
On lit un tuple (coût constant), on lit le tuple vide (coût constant), on effectue une comparaison (coût constant).
On obtient donc un coût constant (quelque soit la taille de la Liste, on aura toujours juste ces 3 opérations basiques).
On lit la variable elt (coût constant), on lit la variable lst (coût constant), on génère un couple en fournissant les deux valeurs précédentes (coût constant).
On obtient donc un coût constant (quelque soit la taille de la Liste, on aura toujours juste ces 3 opérations basiques).
On lit la variable lst (coût constant), et on accède à son indice 0 (coût constant).
On obtient donc un coût constant (quelque soit la taille de la Liste, on aura toujours juste ces 2 opérations basiques).
On lit juste la variable lst (coût constant).
On lit la variable lst (coût constant), et on accède à son indice 0 (coût constant).
On obtient donc un coût constant (quelque soit la taille de la Liste, on aura toujours juste ces 2 opérations basiques).
On lit la variable lst (coût constant), et on accède à son indice 1 (coût constant).
On obtient donc un coût constant (quelque soit la taille de la Liste, on aura toujours juste ces 2 opérations basiques).
On lit la variable lst (coût constant), et on accède à son indice 0 (coût constant).
On obtient donc un coût constant (quelque soit la taille de la Liste, on aura toujours juste ces 2 opérations basiques).
On utilise l'opération primitive acces_tete() (coût constant) puis à l'opération primitive contenu (coût constant).
On obtient donc un coût constant.
Puisque les deux fonctions ont le même coût, on préférera clairement la version qui manipule juste les opérations primitives puisqu'on ne manipule pas directement les données internes. On passe par des fonctions qui le font à notre place.
Il nous manque encore une chose qui pourrait être pratique mais qui ne fait pas partie de l'interface obligatoire : de quoi représenter la liste sans montrer son implémentation mémoire réelle. Il s'agit donc d'une fonction faisant partie de l'Interface Homme Machine.
Nous aimerions afficher '10 -> 15 -> 5' plutôt que de montrer le contenu réel (10, (15, (5, ()))) par exemple.
06° Placer cette fonction representer_liste() parmi vos fonctions d'interface.
1
2
3
4
5
6
7
8 | |
Elle renvoie un string représentant le contenu interne de la Liste de façon totalement arbitraire : le contenu affiché n'a rien à voir avec le type réel (des tuples dans des tuples).
Utiliser les instructions suivantes :
>>> a = inserer_tete(inserer_tete(inserer_tete(nouvelle_liste_vide(), 5), 15), 20)
>>> representer_liste(a)
'20 -> 15 -> 5'
Question : un utilisateur peut-il avoir une idée de l'implémentation interne de notre Liste en utilisant nos fonctions d'interface ?
...CORRECTION...
Non. C'est même le principe fondamental de l'interfaçage : quelque soit l'implémentation interne, l'utilisateur doit pouvoir utiliser les fonctions d'interface pour obtenir les mêmes effets. L'utilisateur ne doit donc pas avoir besoin de connaître l'implémentation interne pour manipuler ses données. Il doit juste utiliser les fonctions d'interface qu'on lui fournit, qui ont certainement étaient optimisées pour gérer ce type de données.
Conclusion
Notre implémentation "Liste Chaînée Tuple (Tête, Queue)" a deux avantages :
- Implémentation qui colle au plus près de la notion de Tête -> Queue.
- Implémentation légère : elle est courte et simple à comprendre. Il faut se souvenir que l'ordre des qualités d'un programme est souvent :
- d'abord de fonctionner,
- ensuite d'être compréhensible facilement pour permettre de le faire évoluer,
- finalement d'être performant.
2 - Création des autres opérations primitives
Ce choix d'implémentation, simple, présente en réalité quelques désavantages. Pour cela, créons d'autres opérations courantes qu'on effectue sur des données de type Liste :
- On veut une fonction longueur()
- On veut une fonction inserer() pour insérer en tant que Cellule d'indice i
- On veut une fonction supprimer() pour supprimer la Cellule d'indice i
- On veut une fonction acces() pour accéder à la Cellule d'indice i
MODULE version 2 : avec des fonctions utilisant les primitives
Voici le programme que vous allez utiliser sur cette deuxième partie : il contient les corrections de la partie 1 ainsi que les fonctions et fonctions de test de la partie 2.
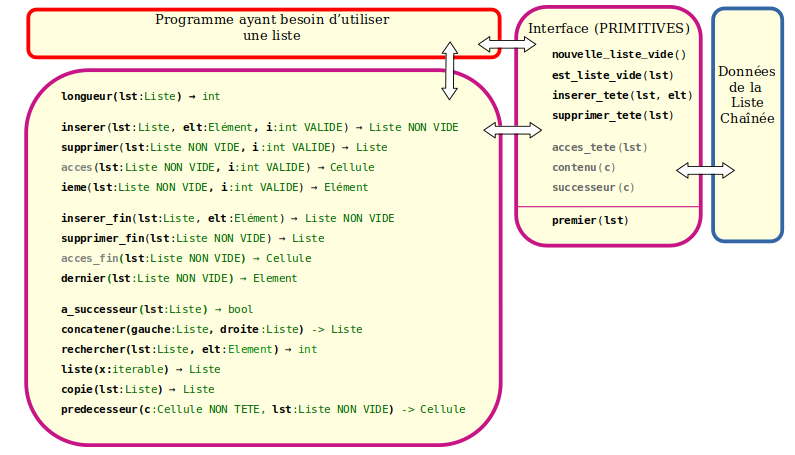
Pour construire toutes nos autres fonctions, nous décidons de choisir les primitives suivantes :
- nouvelle_liste_vide() → Liste VIDE
- est_liste_vide(lst:Liste) → bool
- inserer_tete(lst:Liste, elt:Element) → Liste NON VIDE
- supprimer_tete(lst:Liste NON VIDE) → Liste
- premier(lst:Liste NON VIDE) → Elément
- accesTete(lst:Liste NON VIDE) → Cellule
- contenu(c:Cellule) → Elément
- successeur(c:Cellule) → Cellule|VIDE
Manipulation des listes
On notera que fournir premier() va permettre de manipuler notre liste sans se soucier des Cellules directement. C'est pour cela que acces_tete(), contenu() et successeur() sont grisées : elles existent mais premier() permet de s'en passer.
Manipulation des cellules
Primitives et interfaces
Le module va donc contenir deux types de fonctions :
- Les primitives qui manipulent directement les données.
- Les autres fonctions d'interface qui utilisent les primitives pour fonctionner.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248 | |
07° Utiliser ce nouveau module à la place de l'ancien. Répondre à ces 5 questions :
- Une Liste VIDE peut-elle avoir un Successeur ?
- Que contient la Queue d'une Liste n'ayant qu'un seul élément ? Sa Cellule de tête peut-elle avoir un Successeur ?
- Expliquer pourquoi cette expression vérifie que la liste n'a pas de vrai successeur :
- Formuler en français la question qu'on pose en inversant la réponse precédente ?
- En se souvenant que NON (a OU b) est équivalent à (NON a) ET (NON b), comment aurait-on pu écrire la réponse de la fonction ?
est_liste_vide(lst) or est_liste_vide(supprimer_tete(lst))
not( est_liste_vide(lst) or est_liste_vide(supprimer_tete(lst)) )
...CORRECTION...
- Une Liste VIDE n'a pas de Cellule par défintion. Comme elle n'a pas de Cellule, elle n'a pas non plus de successeur...
- Une Liste n'ayant qu'un seul élément est une Tête suivi d'une Queue vide. La tête de cette liste n'a donc pas de successeur non plus.
- Expliquer pourquoi cette expression vérifie que la liste n'a pas de successeur :
- Formuler en fançais la question qu'on pose à l'interpréteur en inversant la réponse precédente ?
- En se souvenant que NON (a OU b) est équivalent à (NON a) ET (NON b), comment aurait-on pu écrire la réponse de la fonction ?
est_liste_vide(lst) or est_liste_vide(supprimer_tete(lst))
On regroupe les deux cas ci-dessous en le regroupant avec un OU : une Liste VIDE ou une Liste n'ayant qu'un Elément n'a pas de successeur.
not( est_liste_vide(lst) or est_liste_vide(supprimer_tete(lst)) )
L'inverse logique de "N'a pas de successeur" est "A un successeur".
La question qu'on pose est donc "La Liste a-t-elle un successeur ?
not est_liste_vide(lst) and not est_liste_vide(supprimer_tete(lst))
Pour être explicite, on peut placer des parenthèses (mais ce n'est pas nécessaire ici car not est prioritaire sur and et or).
(not est_liste_vide(lst)) and (not est_liste_vide(supprimer_tete(lst)))
08-A° Créer la fonction d'interface longueur() en utilisant les fonctions d'interface est_liste_vide() et supprimer_tete(). Le principe est bien de compter une à une les cellules. Commencer soit par la version récursive, soit par la version itérative puis... faire la version qui vous plait moins.
Prototype
def longueur(lst:'Liste') -> int:
Vous pourrez utiliser la fonction tester_longueur() pour vérifier votre réponse OU comprendre ce qu'on attend de vous. Finalement, les fonctions de test, c'est pratique pour la phase d'écriture non ?
...CORRECTION...
1
2
3
4
5
6 | |
1
2
3
4
5
6
7 | |
08-B° Quel est le coût de votre fonction longueur() ?
09-A° Créer la fonction d'interface acces() en utilisant les fonctions d'interface existantes. Le principe est de se déplacer vers la bonne Cellule. Attention aux préconditions : l'indice i qu'on vous envoie est valide et la liste n'est donc pas vide. Inutile de tester que c'est bien vrai.
Prototype
def acces(lst:'Liste NON VIDE', i:'int VALIDE') -> 'Cellule':
Vous pourrez utiliser la fonction tester_acces().
...CORRECTION...
Beaucoup de versions possibles : récursives ou itératives, avec successeur(), avec supprimer_tete() ou avec supprimer()...
Quelques possibilités :
1
2
3
4
5
6 | |
1
2
3
4
5
6 | |
09-B° Quel est le coût de votre fonction acces() ?
10-A° Créer la fonction d'interface ieme() : elle doit renvoyer l'élément d'indice i. Maintenant que la fonction acces() est réalisée, c'est facile.
Prototype
def ieme(lst:'Liste NON VIDE', i:'int VALIDE') -> 'Element':
Vous pourrez utiliser la fonction tester_ieme().
...CORRECTION...
Beaucoup de versions possibles. Le plus simple est d'utiliser la primitive acces() qu'on vient de créer.
1
2
3 | |
Sinon, on peut partir sur le fait que la liste est immuable : on coupe i tête et on renvoie la valeur de tête de la nouvelle liste, comme dans l'activité précédente.
1
2
3
4
5
6
7 | |
10-B° Quel est le coût de votre fonction ieme() ?
RAPPEL : variable de boucle nommée _ ?
On utilise ce nom de variable de boucle lorsqu'on veut simplement dire qu'on veut faire l'action k fois : for _ in range(10) veut donc dire qu'on va faire le bloc 10 fois.
11° Observer la fonction inserer() ci-dessous.
inserer(lst:Liste, elt:Element, i:'int VALIDE') -> 'Liste NON VIDE'
Renvoie une nouvelle liste où l'élément fourni lst est maintenant l'élément de la liste situé à l'indice i voulu.
PRECONDITION : l'indice doit être un indice VALIDE pour la liste fournie. Transmettre un indice égale à la longueur de la liste, cela veut dire de placer l'élément en fin de liste. Si la liste est vide, le seul indice valide est donc l'indice 0.
listeA = (12, 15, 18, 7)
listeB = inserer(listeA, 5, 2)
listeB contiendra les éléments dans cet ordre : (12, 15, 5, 18, 7).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16 | |
Exemple d'utilisation :
>>> a = inserer_tete(inserer_tete(inserer_tete(nouvelle_liste_vide(), 5), 15), 20)
>>> representer_liste(a)
'20 -> 15 -> 5'
>>> a = inserer(a, 12, 1)
>>> representer_liste(a)
'20 -> 12 -> 15 -> 5'
>>> a = inserer(a, 20, 2)
>>> representer_liste(a)
'20 -> 12 -> 20 -> 15 -> 5'
Questions :
- Expliquer comment fonctionne cette fonction.
- Que vaut le coût de l'insertion d'un nouvel élément dans le pire des cas pour notre implémentation (c'est à dire lorsque l'élément à rajouter est à placer en fin de liste) :
- Le coût est constant : 𝞗(1)
- Le coût est logarithmique : 𝞗(log2 n) ou autre
- Le coût est linéaire : 𝞗(n)
- Le coût est quadratique : 𝞗(n2)
- Le coût est exponentielle : 𝞗(2n ou autre)
- Que vaut le coût de l'insertion d'un nouvel élément dans le meilleur des cas pour notre implémentation (c'est à dire lorsque l'élément à rajouter est à placer en tête de liste) :
- Le coût est constant : 𝞗(1)
- Le coût est logarithmique : 𝞗(log2 n) ou autre
- Le coût est linéaire : 𝞗(n)
- Le coût est quadratique : 𝞗(n2)
- Le coût est exponentielle : 𝞗(2n) ou autre
...CORRECTION...
Pire des cas
Si notre liste possède n éléments, on voudra le placer à l'index n-1.
On remarque qu'on a n-1 opérations de suppression de têtes puis n-1 opérations d'insertion de têtes.
On a donc 2 * (n-1) opérations linéaires à effectuer.
On a donc 2*n - 2 opérations.
Si on néglige le -2 pour les grandes valeurs de n, on obtient 2*n opérations.
On omet le facteur multiplicateur et on voit donc que l'insertion possède un coût en n : il s'agit d'un coût linéaire.
Meilleur des cas
Il suffit de créer un nouveau tuple en allant lire l'adresse de l'ancien tuple, en créant un nouveau tuple (tete, queue) et en renvoyant le résultat : 3 actions élémentaires quelque soit le nombre de données réel dans la liste. Le coût est donc constant quelque soit la longueur n des données.
12-A° Réaliser la fonction supprimer() qui se rapproche de la fonction inserer(). La différence vient de l'action une fois sur place. On supprime la Cellule plutôt que de créer une nouvelle liaison.
...CORRECTION...
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16 | |
12-B° Quel est le coût de votre fonction supprimer() ?
2.1 Accès séquentiel ou accès aléatoire ?
Par définition, une Liste Chaînée est une liste à accès séquentiel : pour trouver un Elément, il faut partir de la tête puis fouiller le successeur, puis le successeur du successeur ect... jusqu'à trouver l'élément voulu.
L'autre possibilité est l'accès aléatoire : avec une telle structure, on peut accéder à n'importe quelle case aussi facilement qu'une autre. Le mot aléatoire est utilisé pour montrer qu'on pourrait choisir une case au hasard et aller la lire directement.
2.2 Coût de l'implémentation en tuple (tête, queue)
Vous venez de créer l'ensemble des opérations primitives permettant de nommer notre structure de données une Liste. Notre implémentation est basée sur la Liste Chaînée qui est la meilleure façon de réaliser une Liste Récursive.
Toutes les actions sur la Tête sont à coût constant (complexité 𝞗(1)).
Dans un cas quelconque :
- La lecture est à coût linéaire (complexité en 𝓞(n) car c'est linéaire ou moins)
- L'insertion et la suppression est à coût linéaire (complexité en 𝓞(n) car c'est linéaire ou moins)
Toutes les actions sur la Fin sont à coût linéaire (complexité 𝞗(n)).
3 - Concaténation et autres créations
Regardons l'un des autres avantages des Listes Chaînées : la concaténation de deux listes.
13-A° Créer la fonction d'interface concatener(). Elle doit parvenir à réaliser une nouvelle Liste à partir de la liste de gauche et de la liste de droite
- La Tête de la nouvelle liste est la Tête de la liste de gauche
- La Fin de la liste de gauche doit mener à la Tête de la liste de droite
- La Fin de la nouvelle liste est la Fin de la liste de droite
Prototype
def concatener(gauche:'Liste', droite:'Liste') -> 'Liste':
Attention, les listes gauche et droite peuvent très bien être vides.
13-B° Si on désigne par nG la longueur de la liste de gauche et par nD la longueur de la liste de droite, quel est le coût de cette opération de concaténation ?
- Coût linéaire par rapport à (nG+nD) et complexité 𝞗(nG+nD)
- Coût linéaire par rapport à (nG+nD) et complexité 𝓞(nG+nD)
- Coût linéaire par rapport à nG et complexité 𝞗(nG)
- Coût linéaire par rapport à nG et complexité 𝓞(nG)
- Coût linéaire par rapport à nD et complexité 𝞗(nD)
- Coût linéaire par rapport à nD et complexité 𝓞(nD)
Voilà, vous en avez fini pour la conception du module. Vous trouverez dans la partie FAQ de nouvelles fonctionnalités pratiques mais dont le coût est malheureusement linéaire. Quelqu'un ne comprennant pas le type Liste Chainée pourrait croire à tord qu'utiliser ces fonctions est très rapide puisqu'on les appelle en n'utilisant qu'une instruction. Vous avez maintenant compris qu'il faut une compréhension fine d'une structure de données pour estimer le coût d'une instruction.
14° En regardant simplement la documentation du module, présentant les fonctions disponibles (voir ci-dessous), quelle est la partie de la Liste Chaînée tuple (Tête, Queue) sur laquelle il est le plus difficile d'intervenir ?
Description du MODULE final LISTE CHAINEE IMMUABLE TETE-QUEUE
88
'''INTERFACE du type Liste Chaînée IMMUABLE basée sur des tuples : () ou (tete, queue)
Description des types non natifs
--------------------------------
Element : le type des éléments disponibles dans votre Liste si elle est homogène.
Cellule : la référence d'un conteneur (Element, Cellule suivante).
Liste : Liste VIDE | Liste NON VIDE.
Opérations primitives de la Liste Chainée
-----------------------------------------
+ CST O(1) nouvelle_liste_vide() -> Liste VIDE
+ CST O(1) est_liste_vide(lst:Liste) -> bool
+ CST O(1) inserer_tete(lst:Liste, elt:Element) -> Liste NON VIDE
+ CST O(1) supprimer_tete(lst:Liste NON VIDE) -> Liste
+ CST O(1) premier(lst:Liste NON VIDE) -> Element
+ CST O(1) acces_tete(lst:Liste NON VIDE) -> Cellule
+ CST O(1) contenu(c:Cellule) -> Element
+ CST O(1) successeur(c:Cellule) -> Cellule|VIDE
Fonctions d'interface supplémentaires
-------------------------------------
+ LIN θ(n) longueur(lst:Liste) -> int
+ LIN O(n) inserer(lst:Liste, elt:Element, i:int VALIDE) -> Liste NON VIDE
+ LIN O(n) supprimer(lst:Liste NON VIDE, i:int VALIDE) -> Liste
+ LIN O(n) acces(lst:Liste NON VIDE, i:int VALIDE) -> Cellule
+ LIN O(n) ieme(lst:Liste NON VIDE, i:int VALIDE) -> Element
+ LIN θ(n) inserer_fin(lst:Liste, elt:Element) -> Liste NON VIDE
+ LIN θ(n) supprimer(lst:Liste NON VIDE, i:int VALIDE) -> Liste
+ LIN θ(n) dernier(lst:Liste NON VIDE) -> Element
+ LIN θ(n) acces_fin(lst:Liste NON VIDE) -> Cellule
+ representer_liste(lst:Liste) -> str
+ CST O(1) a_successeur(lst:Liste) -> bool
+ LIN θ(ng) concatener(gauche:Liste, droite:Liste) -> Liste
+ LIN θ(i) rechercher(lst:Liste, elt:Element) -> int
+ LIN θ(nx) liste(x) -> Liste
+ LIN θ(n) copie(lst:Liste) -> Liste
+ LIN O(n) predecesseur(c:Cellule, lst:Liste NON VIDE) -> Cellule|VIDE
'''
15° Aller chercher le module finalisé dans la partie FAQ. Nous allons réaliser un court programme en utilisant notre module de listes chaînées.
- Etudier la fonction liste() qui permet de générer une liste à partir d'une autre donnée, quelconque : quel est son coût ?
- Placer le module (qu'on nommera liste_chainee_tq.py) au même endroit que le programme suivant. Lancer pour constater le bon fonctionnement.
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205 | |
1
2
3
4
5
6
7
8
9
10
11
12
13 | |
16° Etudier la fonction copie(), expliquer son fonctionnement et déterminer son coût par rapport aux nombres d'éléments n de la liste de base.
1
2
3
4
5
6
7
8
9
10
11
12
13 | |
17° Le prototype de acces_fin() est le suivant :
def acces_fin(lst:'Liste NON VIDE') -> 'Cellule'
Questions
- Expliquer le fonctionnement de cette version non récursive en traduisant une par une ces lignes en français.
- Expliquer le fonctionnement de cette version 2 non récursive en traduisant une par une ces lignes en français.
- Expliquer le fonctionnement de la version récursive qu'on trouve dans le module de la partie FAQ.
- Quel est le coût des 3 versions de acces_fin() ?
1
2
3
4
5 | |
1
2
3
4 | |
1
2
3
4
5
6
7 | |
18° Sachant que acces_fin() est toujours à coût linéaire, quel sera le coût de dernier() ?
def dernier(lst:'Liste NON VIDE') -> 'Elément'
19° Expliquer pourquoi :
- le coût d'une fonction qui chercherait le prédécesseur d'une Cellule aurait un coût linéaire en 𝓞(n) ?
- on a besoin de fournir la liste en plus de la cellule ?
def predecesseur(c:'Cellule', 'Liste NON VIDE') -> 'Cellule|VIDE'
20° Compléter ce programme pour qu'il parvienne bien à implémenter une liste sous forme d'un tuple (tête, queue).
Rappel : une liste VIDE est un tuple vide et une liste NON VIDE est un couple (élément, queue), la queue étant une Liste.
Liste = (Elément, Liste) | ()
Seules les primitives liées à la liste elle-même sont demandées, rien au niveau des Cellules.
Commencez par les 5 fonctions implémentant les primitives.
Passez ensuite aux autres fonctions en n'utilisant que les primitives.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146 | |
CONCLUSION : Primitives et notion d'interfaçage
- Les primitives sont des fonctions bien choisies qui permettent de construire toutes les autres fonctionnalités désirées.
- Les primitives sont les seules à manipuler directement la structure interne réelle de nos données.
- Le rajout de premier() en tant que primitive permet de se passer des primitives liées aux Cellules.
4 - FAQ
On peut avoir le module déjà réalisé ?
Vous pouvez maintenant directement télécharger ce module :
Activité publiée le 14 10 2020
Dernière modification : 03 10 2022
Auteur : ows. h.