Données Graphes 3

Identification

Infoforall

31 - graphe et liste

⏪

⏬

⏩

1 - Sommet

2 - liste

3 - Lst Adj.

4 - Tableaux

5 - lst cha.

6 - orienté

7 - Pondéré

8 - Python

9 - Sujets

10 - FAQ

Documents de cours : open document ou pdf

1 - Implémenter et ordonner les sommets

⇩ ⇧ ⤊

Nous allons voir ici comment stocker de vraies informations liées aux sommets en plus d'un simple numéro ou d'un simple identifiant textuel.

Il existe de multiples façons d'implémenter les données des sommets mais la plupart du temps dans les sujets de BAC, ils ne portent que leurs noms comme information.

Imaginons qu'on veuille encoder la carte d'un donjon contenant des monstres et des trésors à récupérer :

Matrice exemple pour la liste d'adjacence
1.1 Sommet vu comme un couple

Nous utilisons des couples (tuples de 2 cases) où l'indice 0 est l'étiquette de la salle et l'indice 1 un autre tuple contenant les informations sur la salle :

1 2 3 4 5 6 7 8
# Création des sommets avec un tuple contenant un string et un tuple a = ("A", ("Salle de garde", 6, "Gobelin", 100)) b = ("B", ("Antre du Dragon", 1, "Dragon", 2000)) c = ("C", ("Crypte", 3, "Zombie", 200)) d = ("D", ("Salle secrète", 3, "Araignée Géante", 1000)) tresor_en_salle_a = a[1][3]

01° Que ramène l'évaluation de a[1][3] ?

...CORRECTION...

Voici a : ("A", ("Salle de garde", 6, "Gobelin", 100)), un tuple de deux éléments.

Voici a[1] : ("Salle de garde", 6, "Gobelin", 100), un tuple de 4 éléments.

Voici a[1][3] : 100

1.2 Sommet vu comme un tuple

Nous utilisons des tuples où l'indice 0 référence l'étiquette de la salle et les autres indices référencent les informations sur la salle :

1 2 3 4 5 6 7 8
# Création des sommets avec un tuple contenant toutes les infos a = ("A", "Salle de garde", 6, "Gobelin", 100) b = ("B", "Antre du Dragon", 1, "Dragon", 2000) c = ("C", "Crypte", 3, "Zombie", 200) d = ("D", "Salle secrète", 3, "Araignée Géante", 1000) tresor_en_salle_a = a[4]
1.3 Sommet vu comme un dictionnaire

Nous utilisons des dictionnaires où chaque clé correspond à une information sur la salle :

1 2 3 4 5 6 7 8
# Création des sommets avec des dictionnaires a = {"etiquette": "A", "nom": "Salle de garde", "nb": 6, "monstre": "Gobelin", "tresor": 100} b = {"etiquette": "B", "nom": "Antre du Dragon", "nb": 1, "monstre": "Dragon", "tresor": 2000} c = {"etiquette": "C", "nom": "Crypte", "nb": 3, "monstre": "Zombie", "tresor": 200} d = {"etiquette": "D", "nom": "Salle secrète", "nb": 3, "monstre": "Araignée Géante", "tresor": 1000} tresor_en_salle_b = b["tresor"]

02° Que ramène l'évaluation de b["tresor"] ?

...CORRECTION...

Voici b : {"etiquette": "B", "nom": "Antre du Dragon", "nb": 1, "monstre": "Dragon", "tresor": 2000}, un dictionnaire.

Demander b["tresor"] veut donc dire de ramener la valeur associée à la clé "tresor".

On obtient donc 2000.

1.4 Sommet vu comme un objet

Nous utilisons des objets où chaque attribut correspond à une information sur la salle :

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
# Création des sommets avec des objets class Salle: def __init__(self, e, n, nb, m, t): self.etiquette = e self.nom = n self.nb = nb self.monstre = m self.tresor = t a = Salle("A", "Salle de garde", 6, "Gobelin", 100) b = Salle("B", "Antre du Dragon", 1, "Dragon", 2000) c = Salle("C", "Crypte", 3, "Zombie", 200) d = Salle("D", "Salle secrète", 3, "Araignée Géante", 1000) tresor_en_salle_c = c.tresor

03° Que ramène l'évaluation de c.tresor ?

...CORRECTION...

La variable c fait référence à une instance de Salle

Demander c.tresor veut donc dire de ramener la valeur attribuée à l'attribut associée tresor de l'objet "c".

On obtient donc 200.

Maintenant que nous avons vu comment stocker les informations individuelles de chaque sommet, voyons comment stocker celles de tous les sommets.

1.5 Stocker les sommets dans un tableau

Principe

Pour mettre les sommets en mémoire sans se soucier de leur implémentation, le plus simple est de créer un tableau qu'on pourrait nommer sommets : de cette façon, on attribue naturellement un numéro à chaque sommet : son indice dans le tableau.

Remarque : c'est la méthode naturelle utilisée les matrices puisque chaque sommet possède déjà un numéro de ligne et de colonne qui lui est propre.

1 2 3 4 5 6 7
a = ... b = ... c = ... a = ... 0 1 2 3 sommmets = [a, b, c, d]

La salle b serait la salle de numéro 1.

On voit d'ailleurs qu'avec ce système deux salles peuvent porter la même étiquette : c'est leur indice dans le tableau qui joue le rôle de clé primaire.

Lien avec la définition mathématique

Nous avions vu qu'un graphe est défini comme g = (S, A).

Ici, l'ensemble S est donc représenté par le conteneur sommets.

04-A° Quelle est la variable-salle dont l'indice dans le tableau sommets est 2 ? Que va renvoyer sommets[2][1]

1 2 3 4 5 6
a = ("A", "Salle de garde", 6, "Gobelin", 100) b = ("B", "Antre du Dragon", 1, "Dragon", 2000) c = ("C", "Crypte", 3, "Zombie", 200) d = ("D", "Salle secrète", 3, "Araignée Géante", 1000) sommmets = [a, b, c, d]

...CORRECTION...

Il s'agit de c

1
0 1 2 3 sommets = [a, b, c, d]

En évaluant progressivement notre expression, on obtient ceci :

sommets[2][1]

("C", "Crypte", 3, "Zombie", 200)[1]

"Crypte"

1.6 Stocker les sommets dans un dictionnaire

Principe

Pour mettre les sommets en mémoire sans se soucier de leur implémentation , on peut les placer dans un dictionnaire sommets ayant comme clé l'identifiant du sommet et comme valeur associée les données portées par ce sommet.

Attention, pour utiliser cette métohde il faut pouvoir énumérer les clés présentes dans le dictionnaire d'une façon ou d'une autre. C'est le cas en Python avec la méthode keys().

1 2 3 4 5 6
a = ... b = ... c = ... a = ... sommmets = {0:a, 1:b, 2:c, 3:d}

Les données de la salle b sont récupérables en utilisant sommets[1]. Attention, 1 est bien une clé de dictionnaire, pas un indice de tableau.

Par contre, on peut utiliser plutôt un identifiant textuel pour jouer le rôle de clés.

1 2 3 4 5 6
a = ... b = ... c = ... a = ... sommmets = {'a':a, 'b':b, 'c':c, 'd':d}

Les données de la salle b sont récupérables en utilisant sommets['b'].

Lien avec la définition mathématique

Nous avions vu qu'un graphe est défini comme g = (S, A).

Ici, l'ensemble S est donc représenté par le conteneur sommets.keys()

.

04-B° Que va renvoyer sommets['B12']['nom']

1 2 3 4 5 6
a = {"etiquette": "A", "nom": "Salle de garde", "nb": 6, "monstre": "Gobelin", "tresor": 100} b = {"etiquette": "B", "nom": "Antre du Dragon", "nb": 1, "monstre": "Dragon", "tresor": 2000} c = {"etiquette": "C", "nom": "Crypte", "nb": 3, "monstre": "Zombie", "tresor": 200} d = {"etiquette": "D", "nom": "Salle secrète", "nb": 3, "monstre": "Araignée Géante", "tresor": 1000} sommmets = {'E4':a, 'N7':b, 'X8':c, 'B12':d}

...CORRECTION...

sommets['B12']['nom']

{"etiquette": "D", "nom": "Salle secrète", "nb": 3, "monstre": "Araignée Géante", "tresor": 1000}['nom']

"Salle secrète"

En évaluant progressivement notre expression, on obtient ceci :

sommets[2][1]

("C", "Crypte", 3, "Zombie", 200)[1]

"Crypte"

2 - [Rappel] Listes

⇩ ⇧ ⤊

Cette partie est destinée à être commentée au tableau par l'enseignant lors du bilan de l'activité. Vous pouvez donc passer directement à la partie suivante.
(Rappel) 1er partie de la définition de Liste : l'idée générale

A - Propriétés générales d'organisation

Le type abstrait Liste a les propriétés suivantes :

  • Une Liste est une structure LINÉAIRE composée d'une séquence finie et ordonnée de Places contenant chacune un Élement . Si on réalise une analogie avec une armoire à casiers ou dossiers suspendus :
    • L'armoire est la Liste
    • Chaque casier ou dossier suspendu est une Place
    • Chaque objet placé dans un casier ou un dossier suspendu est un Élément
    Analogie des dossiers suspendus
  • On doit pouvoir insérer et supprimer au moins une Place (au choix du concepteur : au début, ou à la fin, ou partout...)
  • On doit pouvoir accéder à toutes les Places.
  • On doit pouvoir lire un Elément en connaissant la Place qu'il occupe
  • On doit pouvoir trouver le successeur unique de chaque Place : en partant d'un casier on doit pouvoir trouver le casier suivant.

On peut donc accéder librement à n'importe quelle donnée de la Liste.

Remarque

Ici, les propriétés ont été données sous forme de simples phrases mais vous verrez dans le supérieur qu'il est possible de les décrire sous forme de propriétés mathématiques.

B - Vocabulaire
  • La première Place de la Liste est nommée tête (head en anglais).
  • L'ensemble des autres Places de la Liste forme la queue (tail en anglais).
  • La dernière Place de la Liste est nommée fin. Attention, on trouve parfois également le mot queue pour désigner la fin. Ici, nous utiliserons bien uniquement fin.
  • L'indice d'une Place correspond au nombre de sauts nécessaires pour l'atteindre à partir de la tête : la tête est à l'indice 0, la suivante 1...
  • La Liste est homogène si tous les éléments stockés sont de même type. Sinon elle est inhomogène.
C - Exemple

On considère une Liste dont

  • La Tête est 5
  • La Queue est 8 → 2 → 3

Deux façons de la représenter :

  • 5 → 8 → 2 → 3
  • 3 ← 2 ← 8 ← 5
Analogie des dossiers suspendus
(Rappel) 2nd partie de la définition de Liste : spécifications des primitives

A - Dépendances du type abstrait Liste

Pour définir notre Liste, nous allons avoir besoin des autres types suivants (ce sont les dépendances) :

  • Vide pour référencer l'absence d'information,
  • Booléen,
  • Entier Naturel,
  • Elément (le type des données que nous allons pouvoir ranger dans la Liste),
  • Place (le conteneur permettant de stocker un Elément). On décide du fait qu'une Place ne peut pas être vide : si elle existe, c'est qu'elle contient un Element.
B - Spécifications : définition

Voici les primitives d'une Liste immuable.

Fondamentales

  1. nLV() ou nouvelleListeVide() → Liste VIDE

    2. Renvoie une nouvelle Liste VIDE initialement.

  2. estLV() ou estListeVide(lst:Liste) → Booléen

    3. Prédicat qui renvoie VRAI si la liste lst fournie est vide, FAUX sinon.

  3. ins() ou inserer(lst:Liste, elt:Elément, ...) → Liste NON VIDE

    4. Renvoie une nouvelle Liste comportant le nouvel élément à une position choisie. Certaines valeurs seront donc décalées par rapport à la Liste initiale.

    POSTCONDITIONS : la Liste renvoyée est NON VIDE et possède un emplacement en plus mais lst est inchangée.

    Voici plusieurs versions qui pourraient convenir, la première étant la plus générique :

    ins() ou inserer(lst:Liste, elt:Elément, i:Entier Naturel VALIDE) → Liste NON VIDE

    Renvoie une nouvelle Liste comportant le nouvel élément à la position indiquée par l'indice fourni.

    insT() ou insererTete(lst:Liste, elt:Elément) → Liste NON VIDE

    Renvoie une nouvelle Liste où l'élément est placé en tête de liste, provoquant le décalage de tous les autres élements.

    Equivalent à un appel à ins() en lui envoyant i=0.

    insF() ou insererFin(lst:Liste, elt:Elément) → Liste NON VIDE

    Renvoie une nouvelle Liste où l'élément est placé en fin de liste.

    Equivalent à un appel à ins() en lui envoyant i=longueur puisque les indices possibles de la liste vont de 0 à longueur-1 avant insertion.

    Un appel à ins() en lui envoyant i=longueur-1 veut dire qu'on veut placer l'élément en avant dernière position, l'ancienne fin est toujours la même.

    Exemples d'utilisation

    lstA = nouvelleListeVide()
    lstB = inserer(lstA, 5, 0)
    lstB contient alors (5, () ) qu'on pourrait noter (5, VIDE).

    lstC = inserer(lstB, 15, 0)
    lstC contient alors (15, (5, () )) qu'on pourrait noter (15, 5, VIDE).

    lstD = inserer(lstC, 25, 1)
    lstD contient alors (15, (25, (5, () ))) qu'on pourrait noter (15, 25, 5, VIDE).

    lstE = inserer(lstD, 50, 3)
    lstE contient alors (15, (25, (5, (50, () )))) qu'on pourrait noter (15, 25, 5, 50, VIDE).

  4. sup() ou supprimer(lst:Liste NON VIDE, ...) → Liste

    5. Renvoie une nouvelle Liste dans laquelle on a supprimé un emplacement prédéfini dans la Liste NON VIDE reçue. Certains emplacements sont donc décalés d'une position par rapport à la Liste initiale.

    PRECONDITION : la Liste reçue est NON VIDE.

    POSTCONDITION : la Liste renvoyée possède un emplacement en moins mais lst est inchangée.

    Voici plusieurs versions qui pourraient convenir, la première étant la plus générique :

    supprimer(lst:Liste NON VIDE, i:Entier Naturel vALIDE) → Liste

    Renvoie une nouvelle Liste dans laquelle on a supprimé l'ancien emplacement ayant cet indice.

    supT() ou supprimerTete(lst:Liste NON VIDE) → Liste

    Renvoie une nouvelle Liste dans laquelle on a supprimé l'ancien emplacement en tête de liste.

    Equivalent à un appel à sup() en lui envoyant i=0.

    supF() ou supprimerFin(lst:Liste NON VIDE) → Liste

    Renvoie une nouvelle Liste dans laquelle on a supprimé l'ancien emplacement en fin de liste.

    Equivalent à un appel à sup() en lui envoyant i=longueur-1.

    Exemple d'utilisation

    Partons de lstE contenant (15, (25, (5, (50, () )))) ou (15, 25, 5, 50, VIDE).
    lstF = sup(lstE, 1)
    lstF contient alors (15, (5, (50, () ))) ou (15, 5, 50, VIDE).

    lstG = sup(lstF, 2)
    lstG contient alors (15, (5, () )) ou (15, 5, VIDE).

Importante si on utilise les indices

  1. longueur(lst:Liste) → Entier Naturel

    2. Renvoie le nombre d'éléments stockés dans la liste.

Interactions avec les Places

  1. acc() ou acces(lst:Liste NON VIDE, ...) → Place

    2. Renvoie la Place correspondant à une position définie.

    POSTCONDITION : la Liste est inchangée.

    Voici plusieurs versions qui pourraient convenir, la première étant la plus générique :

    acc() ou acces(lst:Liste NON VIDE, i:Entier Naturel) → Place

    Renvoie la Place correspondant à l'indice i fourni.

    accT() ou accesTete(lst:Liste NON VIDE) → Place

    Renvoie la Place correspondant à la tête.

    Equivalent à un appel à acc() en lui envoyant i=0.

    accF() ou accesFin(lst:Liste NON VIDE) → Place

    Renvoie la Place correspondant à la fin.

    Equivalent à un appel à acc() en lui envoyant i=longueur-1.

    Les deux dernières primitives (numérotées 7 et 8 ici) interagissent directement avec une Place : la connaissance d'une Place doit venir de l'utilisation de acces().

  2. contenu(plc:Place) → Elément

    3. Renvoie l'Elément référencé par plc.

    POSTCONDITION : si la Liste est homogène le type de l'Elément est compatible avec ceux de la Liste.

  3. succ() ou successeur(plc:Place) → Place|Vide

    4. Renvoie la Place qui succède à plc, ou l'information Vide si elle est la dernière.

Le type abstrait Liste possède donc une définition est plutôt large car

  • on n'explique pas vraiment ce qu'est une Place.
  • on n'impose pas spécifiquement d'endroit où agir. Il faut juste pouvoir agir à un endroit.

Toutes les structures de données qui collent à la définition et qui possèdent ces primitives sont donc des Listes.

Résumé : les 8 types de primitives qu'il faudra avoir ou reconstruire à partir des autres :

Fondamentales

  1. nLV() ou nouvelleListeVide() → Liste VIDE
  2. estLV() ou estListeVide(lst:Liste) → Booléen
  3. ins() ou inserer(lst:Liste, elt:Elément, i:Entier Naturel VALIDE) → Liste NON VIDE
  4. sup() ou supprimer(lst:Liste NON VIDE, i:Entier Naturel VALIDE) → Liste

Importante si on utilise les indices

  1. longueur(lst:Liste) → Entier Naturel

Interactions avec les Places

  1. acc() ou acces(lst:Liste NON VIDE, i:Entier Naturel VALIDE) → Place
  2. contenu(plc:Place) → Elément
  3. succ() ou successeur(plc:Place) → Place|Vide
(Rappel) Implémentations courantes

On implémente souvent les listes sous trois formes.

Tuple (élément de tête, queue) [tuple immuable en Python]

Avec la forme p-uplet (tête, queue), on obtient une structure de données proche d'une pile. Implémentation facile à comprendre mais

  • lecture et modification à coût linéaire (mais constant en tête)
  • rajout et suppression à coût linéaire sur la fin (mais constant en tête)
  • concaténation de deux listes à coût linéaire
    • Serpent Tête et Queue
    Image libre de droit

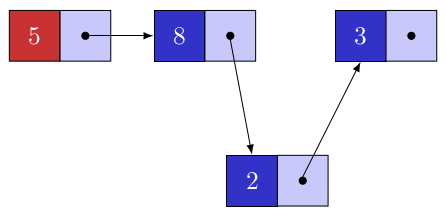
Nous avions l'exemple suivant : 5 → 8 → 2 → 3 qui peut donc être vu comme des couples tête-queue imbriqués les uns dans les autres :

5 →
8 →
2 →
3 → X
Le tableau dynamique [list muable en Python]

La forme liste contiguë. On n'utilise pas de tableau statique car les performances sont alors mauvaises. Par contre, on peut utiliser un tableau dynamique, où les "cases" sont réellement les unes derrière les autres en mémoire. Avec ce tableau dynamique :

  • lecture et modification à coût constant dans le pire des cas
  • rajout et suppression à coût linéaire (mais constant sur la dernière case).
  • concaténation de deux listes à coût linéaire.

Considèrons cette liste :

5 → 8 → 2 → 3

Elle correspondrait à une zone mémoire où toutes les cases ont la même largeur d'octets et sont situées les unes derrière les autres.

5 8 2 3
Liste chaînée [non native en Python]

La forme liste chaînée utilise une succesion de Cellules qui contiennent une valeur ET la référence de la queue : une liste NON VIDE ou une liste VIDE si la Cellule est la Fin de la liste.

  • lecture et modification à coût linéaire (mais constant sur la tête)
  • le rajout et la suppression est à coût linéaire (mais constant sur la tête, parfois la liste intégre une référence vers la Cellule de fin)
  • concaténation de deux listes à coût constant (si on accepte les modifications directes)

Considèrons cette liste :

5 → 8 → 2 → 3

Elle peut donc être vue comme cet ensemble de Cellules :

Liste chaînée

3 - Listes d'adjacence

⇩ ⇧ ⤊

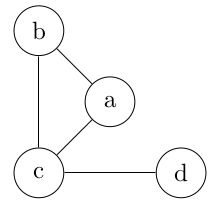
Nous allons voir la liste d'adjacence qui permet d'encoder efficacement un graphe dont la matrice correspondante est plutôt creuse.

3.1 Généralités sur la liste d'adjacence

Liste d'adjacence

L'adjectif adjacent indique que les deux sommets sont reliés par une arête. On dit également voisins.

Une liste d'adjacence est un moyen de représenter un graphe g = (S, A).

On associe à chaque sommet une liste composée des sommets adjacents.

Matrice exemple pour la liste d'adjacence

Sur l'exemple, on a 4 sommets donc 4 listes d'adjacence.

  • Liste d'adjacence du sommet a : b → c
  • Liste d'adjacence du sommet b : a → c
  • Liste d'adjacence du sommet c : a → b → d
  • Liste d'adjacence du sommet d : c
Place mémoire

Notons n le nombre de sommets dans S.

Il faut n listes d'adjacence pour caractériser le graphe (une par sommet). Chaque liste d'adjacence possède au maximum n éléments

La place-mémoire est donc en 𝓞(n*n) donc en 𝓞(n2).

C'est meux qu'avec la matrice d'adjacence qui posséde exactement n éléments par ligne. D'où un coût en 𝞗(n*n) donc en 𝞗(n2)

Arité d'un sommet

L'arité est le nombre de sommets adjacents au sommet.

On obtient facilement l'arité d'un sommet en cherchant la longueur de sa liste d'adjacence .

Une vraie liste ordonnée ? Non

Les listes d'adjacence ne sont pas nécessairement ordonnées, elles n'ont pas d'ordre interne imposé. La tête n'a pas à être associée avec un élément plutôt qu'un autre.

3.2 Liste (ordonnée) d'adjacence

Une liste ordonnée ? Oui !

Ordonner les sommets présente un avantage : on recherche plus facilement si une destination donnée est possible depuis un sommet.

  • Avec un tableau trié, on peut utiliser la recherche dichotomique : 𝓞(lg n) ;
  • Avec une liste chaînée triée, on peut stopper la recherche dès qu'on a dépassé la valeur du sommet cherché : 𝓞(n). Exemple : si on cherche à savoir si un sommet b est adjacent, et qu'on tombe sur c dans la liste, on sait qu'on peut arrêter la recherche : b ne va pas se trouver derrière c.
Avec une liste ordonnée de sommets

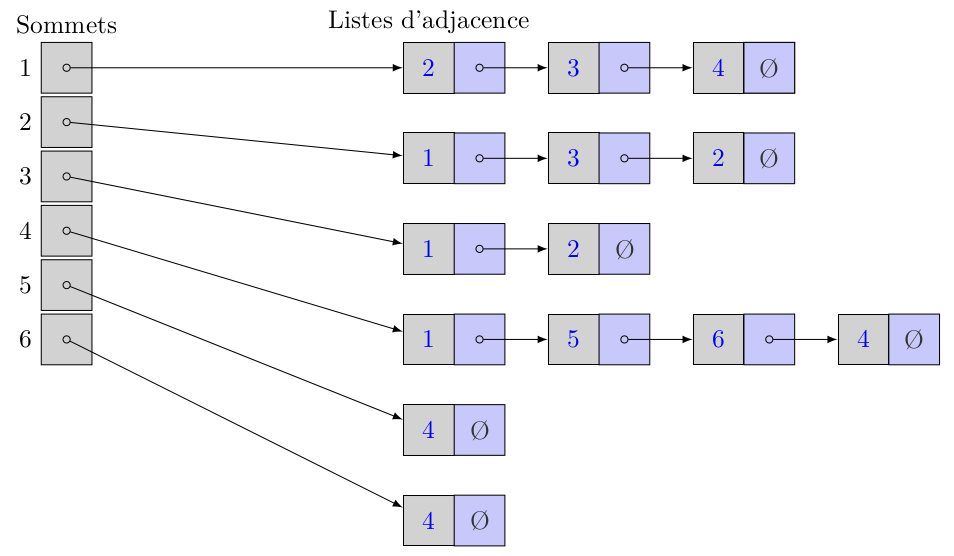
On ordonne les sommets dans l'ensemble S et ensuite on utilise le même ordre d'apparition dans les listes d'adjacence. On obtient alors les listes d'adjacence ci-dessous :

  1. Liste d'adjacence du sommet a ou 0 : 1 → 2
  2. Liste d'adjacence du sommet b ou 1 : 0 → 2
  3. Liste d'adjacence du sommet c ou 2 : 0 → 1 → 3
  4. Liste d'adjacence du sommet d ou 3 : 2

Le numéro d'un sommet n'est pas une simple étiquette (qui pourrait être partagée par plusieurs sommets), mais bien une sorte de "clé primaire".

05° A quoi correspond le nombre d'éléments dans la liste d'adjacence d'un sommet ?

Matrice exemple pour la liste d'adjacence
  1. Liste d'adjacence du sommet a ---- b → c
  2. Liste d'adjacence du sommet b ---- a → c
  3. Liste d'adjacence du sommet c ---- a → b → d
  4. Liste d'adjacence du sommet d ---- c

...CORRECTION...

Cela correspond à son nombre d'arêtes, et donc à son nombre de voisins ou sommets adjacents.

06° Fournir les listes d'adjacences des sommets :

Graphe non orienté q6

...CORRECTION...

  1. Liste d'adjacence du sommet 1 ---- 2 → 3 → 4
  2. Liste d'adjacence du sommet 2 ---- 1 → 3
  3. Liste d'adjacence du sommet 3 ---- 1 → 2
  4. Liste d'adjacence du sommet 4 ---- 1 → 5 → 6
  5. Liste d'adjacence du sommet 5 ---- 4
  6. Liste d'adjacence du sommet 6 ---- 4

Nous avions travaillé avec un bout simplifié de ce plateau Pacman dans l'activité précédente.

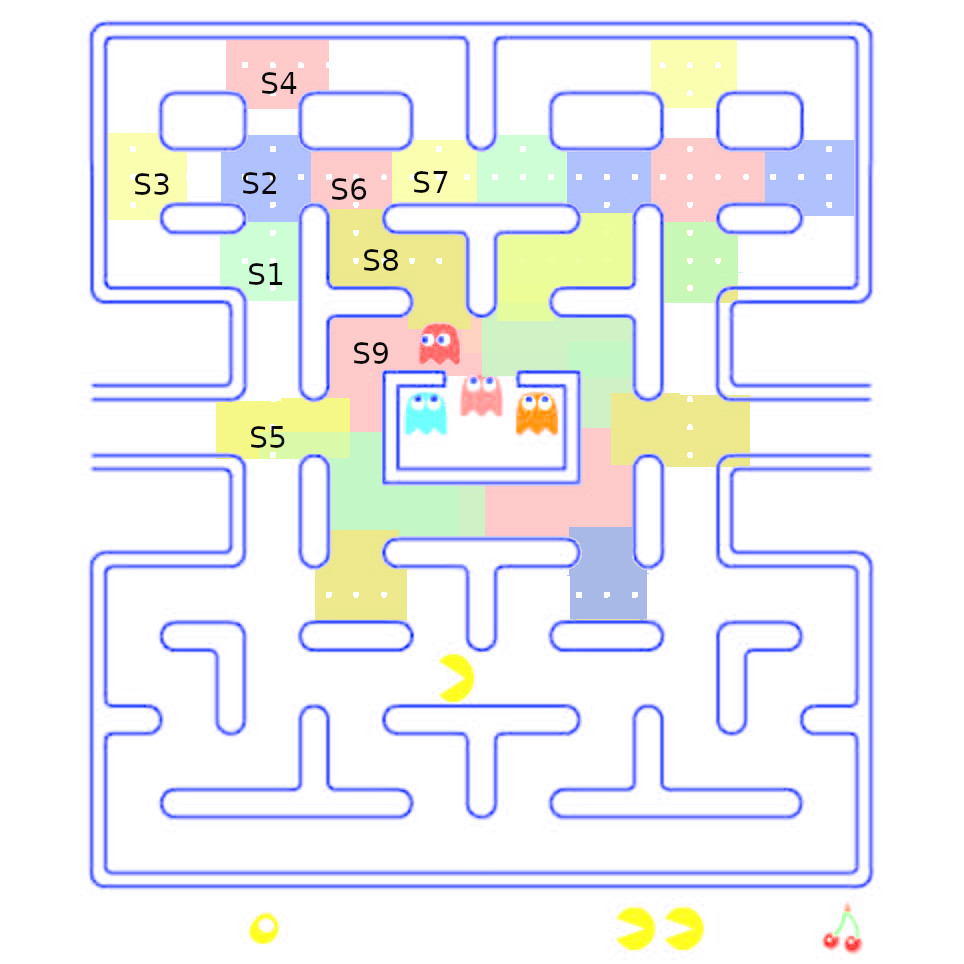
Plateau Pacman

07° Fournir les listes d'adjacences des différents sommets du graphe correspondant aux liaisons entre les différentes zones du plateau du jeu :

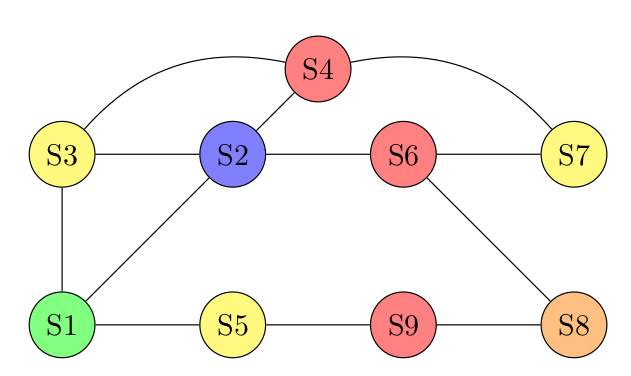
Graphe Pacman
  1. Liste d'adjacence du sommet 1 ----
  2. Liste d'adjacence du sommet 2 ----
  3. Liste d'adjacence du sommet 3 ----
  4. Liste d'adjacence du sommet 4 ----
  5. ...

...CORRECTION...

Graphe Pacman
  1. Liste d'adjacence du sommet 1 ---- 2 → 3 → 5
  2. Liste d'adjacence du sommet 2 ---- 1 → 3 → 4 → 6
  3. Liste d'adjacence du sommet 3 ---- 1 → 2 → 4
  4. Liste d'adjacence du sommet 4 ---- 2 → 3 → 7
  5. Liste d'adjacence du sommet 5 ---- 1 → 9
  6. Liste d'adjacence du sommet 6 ---- 2 → 7 → 8
  7. Liste d'adjacence du sommet 7 ---- 4 → 6
  8. Liste d'adjacence du sommet 8 ---- 6 → 9
  9. Liste d'adjacence du sommet 9 ---- 5 → 8

Vos listes contiennent donc la même information que la matrice d'adjacence correspondante, si ce n'est qu'on n'indique pas les 0. Avec les listes d'adjacences, on ne place en mémoire que l'information "l'arête existe".

Matrice Pacman

4 - Implémenter la liste d'adjacence avec un tableau

⇩ ⇧ ⤊

Il y a beaucoup de façons d'implémenter une liste d'adjacence.

Commençons par l'une des plus courantes : le tableau qui est une structure native dans beaucoup de langages.

4.1 Implémentation des listes d'adjacence en list[list]

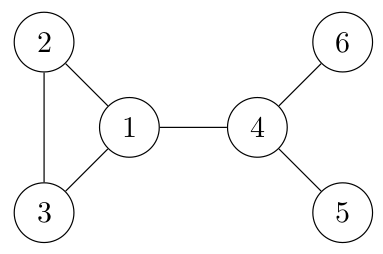
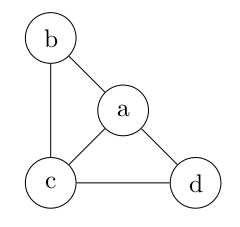
Voici le graphe pris comme exemple :

Matrice exemple pour la liste d'adjacence

Listes d'adjacence des sommets a, b, c et d sont données ci-dessous :

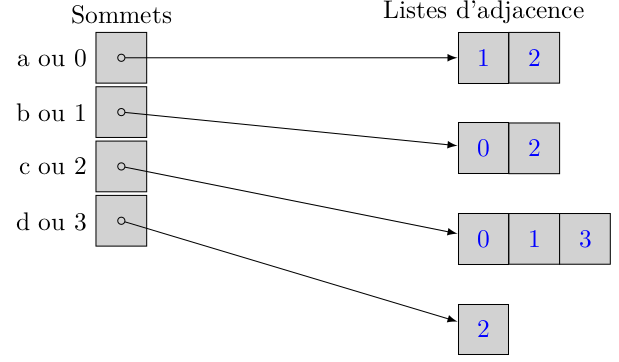
Listes contiguës implémentant des listes d'adjacence

En Python :

1 2 3 4 5 6 7
sommmets = [a, b, c, d] graphe = [ [1, 2], [0, 2], [0, 1, 3], [2]]

Avantage par rapport à la matrice d'adjacence : on ne gère que les arêtes qui existent, espace mémoire en 𝓞(n2). On a 𝞗(n2) avec une matrice.

Désavantage par rapport à la matrice d'adjacence : pour savoir si une arête existe, il faut lire la liste (coût linéaire en 𝓞(n)). On a 𝞗(1) avec une matrice..

08° Quel est le coût d'une recherche d'arête entre deux sommets en utilisant une liste d'adjacence ? Fournir une justification en parlant du pire des cas et du meilleur cas.

  1. Constant : 𝓞(1)
  2. Logarithmique : 𝓞(log n)
  3. Linéaire : 𝓞(n)
  4. Quasi-linéaire : 𝓞(n log n)

...CORRECTION...

Il va falloir lire les éléments de la liste d'adjacence d'un des deux sommets jusqu'à trouver le second sommet.

Dans le pire des cas, le second sommet n'est pas présent dans la liste : le coût de cette recherche est donc linéaire puisqu'on va parcourir toute la liste.

Dans le meilleur des cas, le second sommet est le premier sommet de la liste. Le coût de la recherche est donc constant.

Dans le cas général, on obtient donc un coût 𝓞(n) qui exprime bien qu'il est linéaire ou moins.

Pour rappel, savoir si une arête existe est à coût constant dans une matrice d'adjacence.

m[ligne][colonne]

Puisque chaque accès à une case d'un tableau est à coût constant (modèle RAM), on a deux actions à coût constant, donc l'action totale est à coût constant.

Selon les problèmes, la liste d'adjacence d'un sommet peut avoir une taille limitée. Prenons le cas de PacMan :

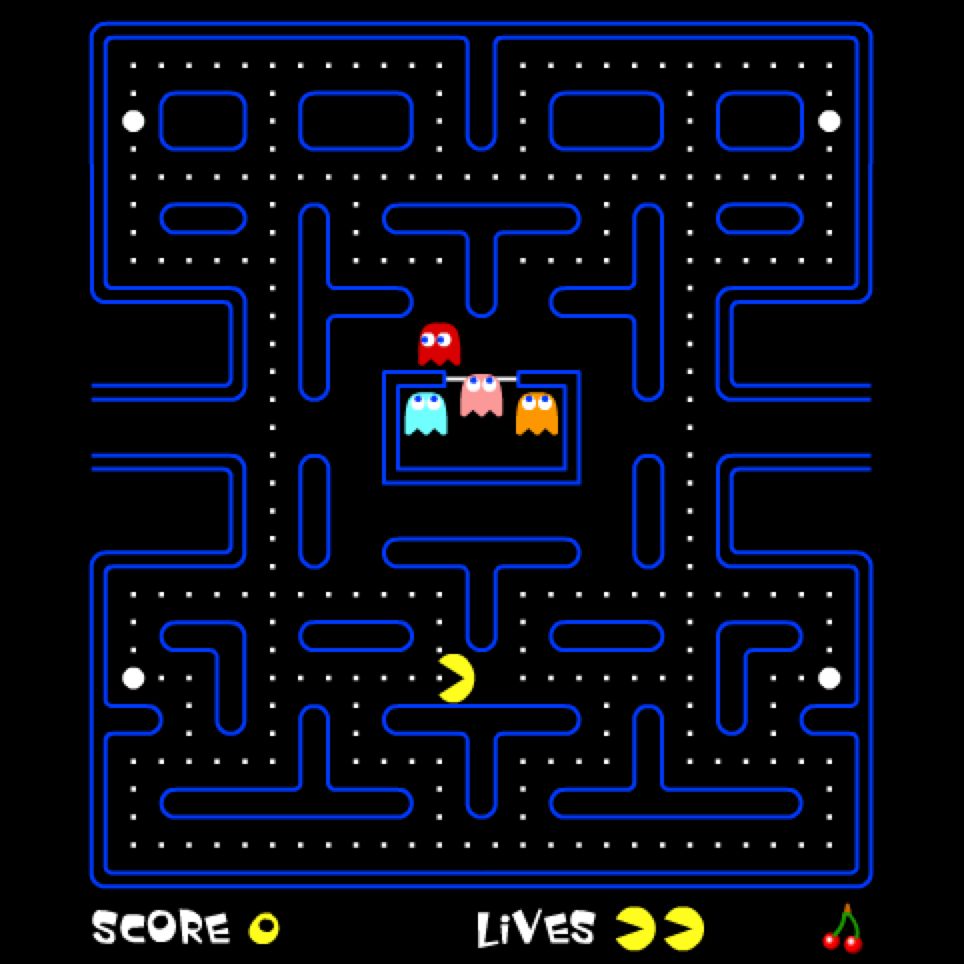
Plateau Pacman

Si on crée un graphe où chaque sommet est bien un point (et pas une zone comme dans la version simplifiée précédente), chaque liste d'adjacence est de taille 4 au maximum puisque chaque sommet ne peut avoir que 4 voisins au maximum : en haut, en bas, à gauche, à droite.

09° Dans le cadre du jeu Pacman, quel est le coût dans le pire des cas de cette recherche d'arête entre deux sommets connus ? Fournir une justification.

  1. Constant : 𝓞(1)
  2. Logarithmique : 𝓞(log n)
  3. Linéaire : 𝓞(n)
  4. Quasi-linéaire : 𝓞(n log n)

...CORRECTION...

Quelque soit le nombre de sommets représentant le labyrinthe, la liste d'adjacence possède 4 sommets au maximum : il faudra donc faire 4 recherches au maximum.

Dans le pire des cas : 4 recherches quelque soit l'ordre n du grahe. C'est donc une opération à coût constant.

Dans le meilleur des cas : une seule recherche. Le coût est donc constant.

Le coût est constant sur ce cas particulier du Pacman.

On notera 𝓞(1), ou même mieux si on proposait ce choix dans le QCM : 𝞗(1).

4.2 Implémentation des listes d'adjacence dans deux tableaux

Principe

Cette autre implémentation est basée sur deux tableaux :

  • debuts qui contient l'indice où débute la liste d'adjacente du sommet voulu et
  • adjacents qui contient la concaténation de toutes les listes précédentes.
1 2 3 4 5
sommmets = [a, b, c, d] debuts = [0, 2, 4, 7] adjacents = [1, 2, 0, 2, 0, 1, 3, 2]
Exemple d'utilisation

Regardons comment trouver la liste d'adjacence du sommet b identifié par l'indice 1.

On lit debuts[1] pour trouver le début de notre liste d'adjacence et la case suivante pour connaitre le début de la prochaine liste d'adjacence.

debuts = [0, 2, 4, 7]

On voit donc que la liste de b commence sur l'indice 2 et que l'indice 4 correspond au début de la prochaine liste.

Conclusion : la liste d'adjacence de b est composée des indices 2 et 3 du tableau adjacents.

Allons lire ce tableau sur ces deux cases :

adjacents = [1, 2, 0, 2, 0, 1, 3, 2]

10° Contruire les deux tableaux debuts et adjacents nécessaires pour représenter ce graphe.

1 2 3 4 5
sommets = [a, b, c, d] debuts = [] adjacents = []
Rajout d'une arête

...CORRECTION...

1 2 3 4 5
sommets = [a, b, c, d] debuts = [0, 3, 5, 8] adjacents = [1, 2, 3, 0, 2, 0, 1, 3, 0, 2]

5 - Implémenter les listes d'adjacence avec des listes chaînées

⇩ ⇧ ⤊

Python ne possède pas de types natifs "listes chaînées". En Python, nous utiliserions juste le type list qui est un tableau dynamique.

D'autres langages possèdent des listes chaînées natives. Dans cette partie, nous allons juste réfléchir aux coûts de différentes opérations si nous utilisons des listes chaînées.

Nous travaillons toujours avec ce graphe :

Matrice exemple pour la liste d'adjacence

Et voici la représentation des arêtes sous forme de listes d'adjacence implémentées sous forme de listes chaînées cette fois.

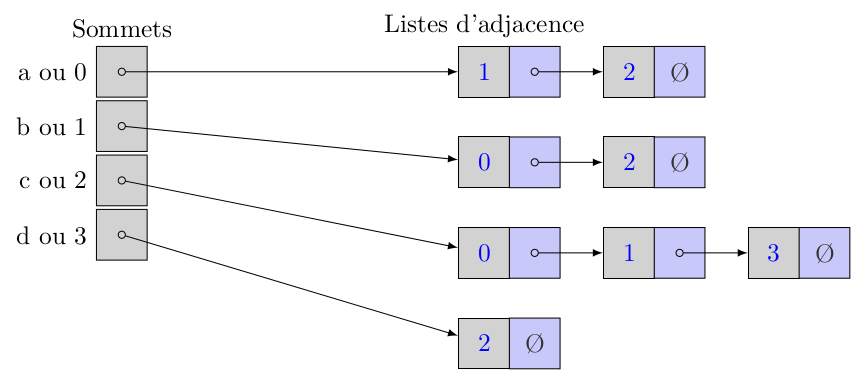
Listes chaînées implémentant des listes d'adjacence

11° Dans le pire des cas, quel est le coût de la recherche d'une arête entre deux sommets connus avec cette implémentation ?

  1. Constant : Θ(1)
  2. Logarithmique : Θ(log n)
  3. Linéaire : Θ(n)
  4. Quasi-linéaire : Θ(n log n)

...CORRECTION...

Il s'agit d'une liste chaînée : on part de la tête et on doit ensuite suivre la chaîne en passant progressivement par toutes les cellules jusqu'à tomber sur la bonne.

Le coût est donc linéaire.

12° On désire transformer le graphe en rajoutant une arête {a, d}. On la rajoute au début de la liste d'adjacence. Quel est le coût de cette opération si on connaît la référence de la tête ?

  1. Constant : Θ(1)
  2. Logarithmique : Θ(log n)
  3. Linéaire : Θ(n)
  4. Quasi-linéaire : Θ(n log n)
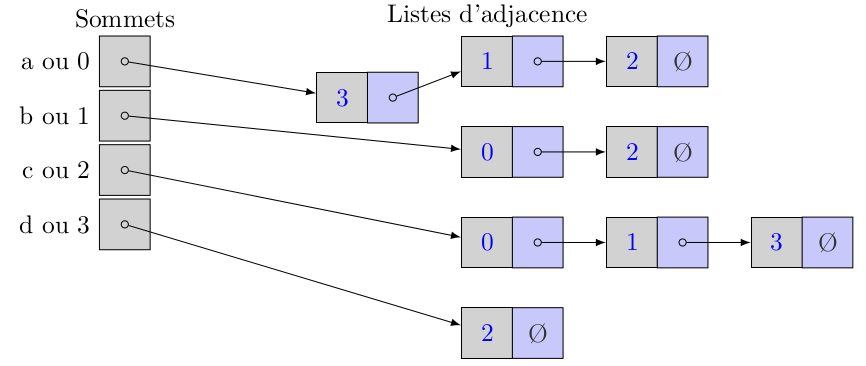
Rajout d'une arête Rajout d'une arête au début

...CORRECTION...

Coût constant car il suffit de :

  • Localiser la tête actuelle : coût constant.
  • Créer la nouvelle Cellule : coût constant.
  • Indiquer que la nouvelle cellule mène à la la tête actuelle : coût constant.
  • Dire que la tête de notre liste est maintenant notre nouvelle Cellule : coût constant.

13° Le problème de la question précédente : la liste d'adjacence de a n'est plus triée. On désire alors plutôt rajouter le sommet 3 (d) à la fin de la liste d'adjacence. Quel est le coût de cette opération si on connaît la référence de la dernière cellule de la liste d'adjacence ?

  1. Constant : Θ(1)
  2. Logarithmique : Θ(log n)
  3. Linéaire : Θ(n)
  4. Quasi-linéaire : Θ(n log n)
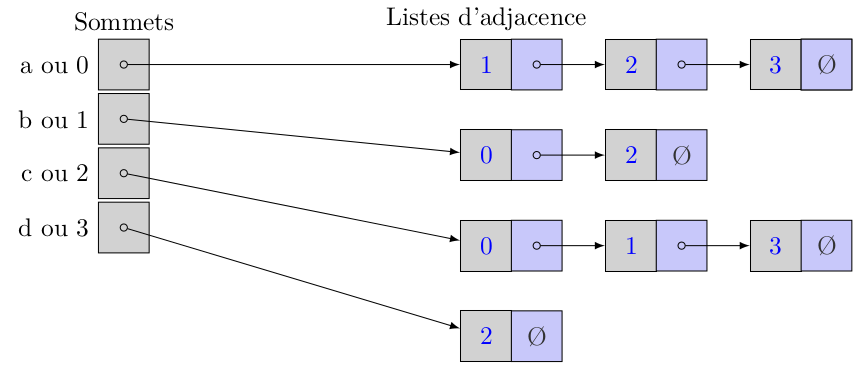
Rajout d'une arête Rajout d'une arête au début

...CORRECTION...

Il s'agit juste de faire ceci :

  1. Localiser la Fin de la liste d'adjacence de a :
    • linéaire si on part de la Tête ou
    • constant si la liste contient directement la référence de la Fin.
  2. Créer la nouvelle Cellule : coût constant.
  3. Indiquer que l'ancienne Fin mène à notre nouvelle Cellule : coût constant.
  4. Modifier éventuellement l'attribut Fin de la liste : coût constant.

En prenant le coût le moins favorable des 4 phases, on voit que le coût est donc constant ou linéaire en fonction de la façon dont la liste a été conçue : liste ne pointant que la cellule de tête, ou liste pointant sa tête et sa fin.

14° Voici un graphe non orienté (et non pur car possèdant des boucles). Fournir les listes d'adjacences qui permettraient de le représenter correctement.

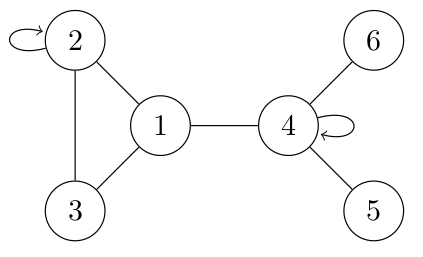
Graphe avec boucle

On utilisera juste les numéros des sommets. Début de la rédaction :

Début de la réponse

...CORRECTION...

réponse

6 - Pour les graphes orientés ? 2 listes !

⇩ ⇧ ⤊

Et sur les graphes orientés ?

6.1 graphe orienté : deux listes d'adjacence

Si le graphe est orienté, il distingue les arcs entrants et les arcs sortants.

Définitions des deux listes d'adjacence

L'une des solutions pour gérer les graphes orientés est de distinguer deux listes d'adjacence :

  1. La liste des successeurs pour les arcs sortants
  2. La liste des prédécesseurs pour les arcs entrants

Si seule la "marche avant" vous intéresse, il suffit d'implémenter uniquement la liste des successeurs.

6.2 Listes des successeurs d'un graphe orienté

Principe

Considérons ce graphe représentant un ensemble de routes, certaines étant à sens unique :

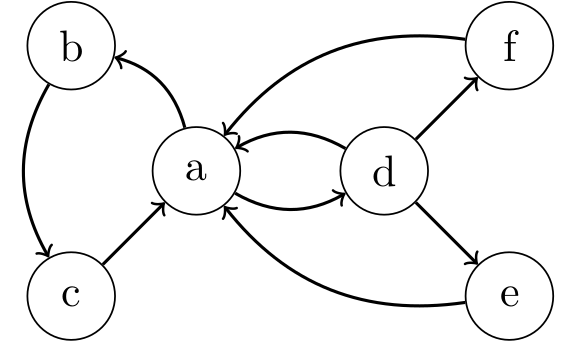
graphe orienté

On voit qu'il n'y a que les arcs (a,b) et (a,d) en sortie du sommet a.

    Listes des successeurs

  • Liste des successeurs du sommet a ---- b → d
  • Liste des successeurs du sommet b ---- c
  • Liste des successeurs du sommet c ---- a
  • Liste des successeurs du sommet d ---- a → e → f
  • Liste des successeurs du sommet e ---- a
  • Liste des successeurs du sommet f ---- a

L'étude de ces listes permet de trouver facilement les culs de sacs (les sommets à partir desquelles on ne peut plus aller nulle part) ou au contraire les sommets menant à une grande partie des autres sommets. On parle de puit.

Exemple avec des tableaux
1 2 3 4 5 6 7
successeurs = [ [1, 3], # successeurs de a, indice 0 [2], # successeurs de b, indice 1 [0], # successeurs de c, indice 2 [0, 4, 5], # successeurs de d, indice 3 [0], # successeurs de e, indice 4 [0]] # successeurs de f, indice 5
6.3 Listes des prédécesseurs d'un graphe orienté

Principe

Pour chaque sommet, on s'intéresse aux sommets qui mènent à ce sommet.

On s'intéresse donc à une sorte de marche arrière.

graphe orienté

    Listes des prédécesseurs

  • Liste des prédécesseurs du sommet a ---- c → d → e → f
  • Liste des prédécesseurs du sommet b ---- a
  • Liste des prédécesseurs du sommet c ---- b
  • Liste des prédécesseurs du sommet d ---- a
  • Liste des prédécesseurs du sommet e ---- d
  • Liste des prédécesseurs du sommet f ---- d

Cette liste vous permet de voir par où on a pu arriver pour atteindre un sommet.

Exemple avec des tableaux
1 2 3 4 5 6 7
predecesseurs = [ [2, 3, 4, 5], # Prédécesseurs de a, indice 0 [0], # Prédécesseurs de b, indice 1 [1], # Prédécesseurs de c, indice 2 [0], # Prédécesseurs de d, indice 3 [3], # Prédécesseurs de e, indice 4 [3]] # Prédécesseurs de f, indice 5

15° Voici un graphe non orienté. Fournir les listes de successeurs et des prédécesseurs qui permettraient de le représenter correctement.

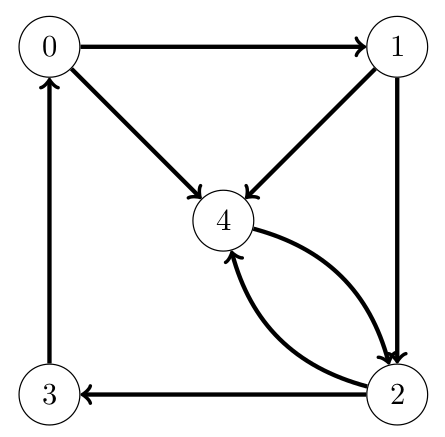
Graphe orienté

...CORRECTION...

    Listes des successeurs

  • Liste des successeurs du sommet 0 ---- 1 → 4
  • Liste des successeurs du sommet 1 ---- 2 → 4
  • Liste des successeurs du sommet 2 ---- 3 → 4
  • Liste des successeurs du sommet 3 ---- 0
  • Liste des successeurs du sommet 4 ---- 2

    Listes des prédécesseurs

  • Liste des successeurs du sommet 0 ---- 3
  • Liste des successeurs du sommet 1 ---- 0
  • Liste des successeurs du sommet 2 ---- 1 → 4
  • Liste des successeurs du sommet 3 ---- 2
  • Liste des successeurs du sommet 4 ---- 0 → 1 → 2

7 - Graphe pondéré

⇩ ⇧ ⤊

Si le graphe est pondéré (comme dans le cas d'une représentation d'un système autonome sous OSPF), il faut rajouter le poids de l'arête ou de l'arc en plus de sa simple existence.

7 graphe pondéré : intégration du poids dans la liste

L'un des moyens de faire cela est de stocker un tableau ou un tuple (destination, poids) plutôt que juste la destination de l'arc ou l'arête.

Prenons par exemple ce petit système autonome qu'on peut représenter par un graphe non orienté:

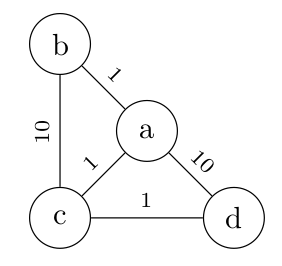
Système autonome sous OSPF

Pour représenter correctement ce système avec une liste d'adjacence, il faut donc une liste correspondant à ceci :

  1. Liste d'adjacence du sommet a ---- (b, 1) → (c, 1) → (d, 10)
  2. Liste d'adjacence du sommet b ---- (a, 1) → (c, 10)
  3. Liste d'adjacence du sommet c ---- (a, 1) → (b, 10) → (d, 1)
  4. Liste d'adjacence du sommet d ---- (a, 10) → (c, 1)

Rien de très compliqué, il suffit de comprendre que la liste d'adjacence porte maintenant deux informations dans chacune de ses cases.

16° Quelle est ou quelles sont les modifications à faire si le graphe du réseau autonome devient ceci :

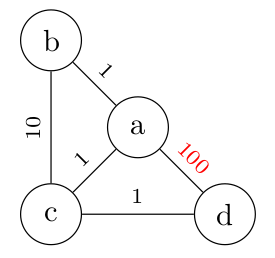
Modification du graphe non orienté

...CORRECTION...

Il faut modifier ici les informations de l'arête (a,d) à deux endroits.

  1. Liste d'adjacence du sommet a ---- (b, 1) → (c, 1) → (d, 100)
  2. Liste d'adjacence du sommet b ---- (a, 1) → (c, 10)
  3. Liste d'adjacence du sommet c ---- (a, 1) → (b, 10) → (d, 1)
  4. Liste d'adjacence du sommet d ---- (a, 100) → (c, 1)

8 - Implémenter une liste d'adjacence avec un dictionnaire

⇩ ⇧ ⤊

Lorsqu'on veut mettre les listes d'adjacence en mémoire, nous avons donc vu qu'on pouvait utiliser :

  • des tableaux dynamiques
  • des listes chaînées

Le créateur de Python, Guido van Rossum, recommande d'utiliser une autre structure pour implémenter les listes d'adjacence lorsqu'on utilise Python : les dictionnaires. C'est d'ailleurs ce que nous avons utiliser dans l'activité Données 29.

Pourquoi utiliser un dictionnaire ? Simplement à cause des performances :

  • Accès en lecture ou en modification d'une valeur connaissant sa clé : coût quasi-constant
  • Rajout d'une valeur connaissant sa clé : coût quasi-constant
  • Suppression d'une valeur connaissant sa clé : coût quasi-constant

Si le graphe est dynamique et change souvent, c'est donc un gros avantage. Par contre, s'il change peu mais qu'il est très grand, les tableaux ou les listes chaînées permettront plus facilement de réduire la place mémoire.

8.1 Graphe pondéré : Listes d'adjacence avec un dictionnaire de dictionnaires

adj sous forme d'un dict[dict]

Les listes d'adjacence peuvent être stockées via un dictionnaire de dictionnaires, nommé adj ci-dessous.

Ce graphe non orienté pondéré représente des routeurs OSPF ou n'importe quoi d'autres (par exemple depuis combien de temps les deux personnes se connaissent) :

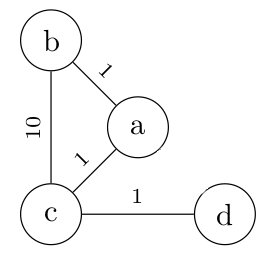
Graphe de liaison entre routeurs

On définit le graphe sous forme de deux dictionnaires :

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
sommets = {} sommets['a'] = {'nom': 'alice', 'age':18} sommets['b'] = {'nom': 'bob', 'age': 19} sommets['c'] = {'nom': 'Charlie', 'age' : 17} sommets['d'] = {'nom': 'dana', 'age':18} adj = {} adj['a'] = {'b': 1, 'c': 1} adj['b'] = {'a': 1, 'c': 10} adj['c'] = {'a': 1, 'b': 10, 'd': 1} adj['d'] = {'c': 1} graphe = (sommets, adj)

Dans sommets, les clés/valeurs correspondent à l'identifiant et aux informations des routeurs.

Dans adj, les clés correspondent à l'identifiant du routeur et la valeur est un autre dictionnaire {id:cout} où id est l'identifiant d'un autre routeur en liaison direct et cout, le coût OSPF.

Si on utilise ce code, voici comment obtenir la valeur de l'arête entre a et b :

>>> graphe[1]['a']['b'] 1
Récupération d'informations

Pour comprendre comment cela fonctionne, il faut y aller progressivement :

>>> graphe[1]['a']['b'] équivalent en mémoire à >>> adj['a']['b'] >>> adj['a']['b'] équivalent en mémoire à >>> {'b': 1, 'c': 1}['b'] >>> {'b': 1, 'c': 1}['b'] >>> 1

Attention aux cléx inexistantes, cela lève une exception. Il faudra donc gérer ces cas problématiques dans les algorithmes.

>>> graphe[1]['a']['d'] KeyError: 'd'

17° Créer la fonction arete qui renvoie le poids de l'arête entre les sommets s1 et s2 (PRECONDITION : sommets qui existent bien dans le graphe):

1 2
def arete(g:tuple, s1:str, s2:str) -> int: return None

g est bien entendu le tuple encodant le graphe.

Exemple :

>>> arete(graphe, 'a', 'b') 1 >>> arete(graphe, 'a', 'd') 0

...CORRECTION...

1 2 3 4 5 6 7 8 9 10 11
def arete(g:tuple, s1:str, s2:str) -> int: liste = g[1] # si s1 et s2 ont bien une liste d'adjacence if s1 in liste.keys() and s2 in liste.keys(): # si s1 et s2 ont bien une liste d'adjacence # si s2 est bien dans la liste de s1 et inversement if s2 in liste[s1].keys() and s1 in liste[s2].keys(): return liste[s1][s2] return 0

18° Créer la fonction nb_aretes qui renvoie le nombre d'arêtes liées à ce sommet:

1 2
def nb_aretes(g:tuple, s:str) -> int: return 0

g est bien entendu le tuple encodant le graphe.

PRECONDITON : le sommet fourni doit être un sommet du graphe.

>>> nb_aretes(graphe, 'a') 2 >>> nb_aretes(graphe, 'c') 3

...CORRECTION...

1 2 3 4
def nb_aretes(g:tuple, s:str) -> int: liste = g[1] if s in liste.keys(): # si s a bien une liste d'adjacence # si s2 est bien dans la liste de s1 et inversement return len(liste[s])

19° On veut en réalité détecter les erreurs en cas de mauvais sommet. Enlever les protections éventuelles sur votre fonction : elle doit lever une exception si on lui envoie un mauvais sommet.

1 2
def nb_aretes(g:tuple, s:str) -> int: return 0

La seule différence dans l'énoncé vient donc de la nature de l'information renvoyée : la fonction renvoie bien un entier ou plante...

>>> nb_aretes(graphe, 'a') 2 >>> nb_aretes(graphe, 'c') 3 >>> nb_aretes(graphe, 'z') KeyError: 'z'

...CORRECTION...

1 2
def nb_aretes(g:tuple, s:str) -> int: return len(g[1][s])

20° Créer la fonction amis_communs qui renvoie un tableau contenant les amis que deux sommets s1 et s2 ont en commun.

1 2
def amis_communs(g:tuple, s1:str, s2:str) -> list: return []
>>> amis_communs(graphe, 'a', 'b') ['c'] >>> amis_communs(graphe, 'a', 'd') ['c']

...CORRECTION...

Deux façons de faire.

1 2 3 4 5 6 7 8 9 10 11 12 13
def amis_communs(g:tuple, s1:str, s2:str) -> list: reponse = [] for s in g[1][s1].keys(): if s in g[1][s2].keys(): reponse.append(s) return reponse def amis_communs(g:tuple, s1:str, s2:str) -> list: reponse = [] for s in g[1][s1].keys(): if s in g[1][s2].keys(): reponse = reponse + [s] return reponse
8.2 Graphe non pondéré : listes d'adjacence avec un dictionnaire de tableaux

Voyons par exemple comment représenter un graphe non orienté et non pondéré comme celui-ci représentant les liaisons sociales entre plusieurs personnes :

Matrice exemple pour la liste d'adjacence
Mauvaise idée pour du non orienté ? adj sous forme d'un dict[dict]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
sommets = {} sommets['a'] = {'nom': 'alice', 'age':18} sommets['b'] = {'nom': 'bob', 'age': 19} sommets['c'] = {'nom': 'Charlie', 'age' : 17} sommets['d'] = {'nom': 'dana', 'age':18} adj = {} adj['a'] = {'b': 1, 'c': 1} adj['b'] = {'a': 1, 'c': 1} adj['c'] = {'a': 1, 'b': 1, 'd': 1} adj['d'] = {'c': 1} graphe = (sommets, adj)

Un peu dommage d'utiliser un dictionnaire alors que la seule valeur associée sera 1.

Bonne idée ? adj sous forme d'un dict[list]

Les listes d'adjacence sont stockées dans un dictionnaire dont les valeurs associées sont les tableaux des sommets adjacents.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
sommets = {} sommets['a'] = {'nom': 'alice', 'age':18} sommets['b'] = {'nom': 'bob', 'age': 19} sommets['c'] = {'nom': 'charlie', 'age' : 17} sommets['d'] = {'nom': 'dana', 'age':18} adj = {} adj['a'] = ['b', 'c'] adj['b'] = ['a', 'c'] adj['c'] = ['a', 'b', 'd'] adj['d'] = ['c'] graphe = (sommets, adj)

21° g est bien entendu le tuple encodant le graphe. Créer la fonction arete qui renvoie un booléen indiquant si l'arête existe, ou pas.

1 2
def arete(g:tuple, s1:str, s2:str) -> bool: return False

Exemple :

>>> arete(graphe, 'a', 'b') True >>> arete(graphe, 'a', 'd') False

...CORRECTION...

22° Créer la fonction nb_aretes qui renvoie le nombre d'arêtes liées à ce sommet (PRECONDTION : le sommet est bien un sommet du graphe):

1 2
def nb_aretes(g:tuple, s:str) -> int: return 0

g est bien entendu le tuple encodant le graphe.

>>> nb_aretes(graphe, 'a') 2 >>> nb_aretes(graphe, 'c') 3

...CORRECTION...

1 2 3 4
def nb_aretes(g:tuple, s:str) -> int: liste = g[1] if s in liste.keys(): # si s a bien une liste d'adjacence # si s2 est bien dans la liste de s1 et inversement return len(liste[s])

23° Créer la fonction amis_communs qui renvoie un tableau contenant les amis que deux sommets s1 et s2 ont en commun.

1 2
def amis_communs(g:tuple, s1:str, s2:str) -> list: return []
>>> amis_communs(graphe, 'a', 'b') ['c'] >>> amis_communs(graphe, 'a', 'd') ['c']

...CORRECTION...

Deux façons de faire.

1 2 3 4 5 6 7 8 9 10 11 12 13
def amis_communs(g:tuple, s1:str, s2:str) -> list: reponse = [] for s in g[1][s1]: if s in g[1][s2]: reponse.append(s) return reponse def amis_communs(g:tuple, s1:str, s2:str) -> list: reponse = [] for s in g[1][s1]: if s in g[1][s2]: reponse = reponse + [s] return reponse

9 - Simplification lors des sujets écrits

⇩ ⇧ ⤊

9.1 Graphe pondéré et sujet écrit

Dans les sujets papier, la seule information portée par chaque sommet est habituellement son nom.

Inutile alors de définir sommets, caractérisant S l'ensemble des sommets.

On peut considérer que les listes d'adjacence caractérisent totalement le graphe.

1 2 3 4 5 6
graphe = {} graphe['a'] = {'b': 1, 'c': 1} graphe['b'] = {'a': 1, 'c': 10} graphe['c'] = {'a': 1, 'b': 10, 'd': 1} graphe['d'] = {'c': 1}

Et si vous avez besoin d'obtenir l'ensemble S des sommets ?

Il suffit d'utiliser graphe.keys().

Et si vous voulez vraiment un tableau : list(graphe.keys()).

9.2 Graphe non pondéré et sujet écrit

Dans les sujets papier, la seule information portée par chaque sommet est habituellement son nom.

Inutile alors de définir sommets, caractérisant S l'ensemble des sommets.

On peut considérer que les listes d'adjacence caractérisent totalement le graphe.

1 2 3 4 5 6
graphe = {} graphe['a'] = ['b', 'c'] graphe['b'] = ['a', 'c'] graphe['c'] = ['a', 'b', 'd'] graphe['d'] = ['c']

10 - FAQ

⇩ ⇧ ⤊

Rien pour le moment

Vous savez maintenant qu'on peut encoder les arcs et arêtes des graphes :

  • soit à l'aide d'une matrice d'adjacence
  • soit à l'aide d'une liste d'adjacence (sous forme de tableaux, de listes chaînées ou de dictionnaire)

Les dernières activités sur les graphes vous montreront comment le parcourir pour y trouver un chemin, une boucle ou une caractéristique particulière.

Activité publiée le 08 04 2021
Dernière modification : 26 04 2021
Auteur : ows. h.


⏪

⏫

⏩